非局域Alice-Bob Benjamin-Ono系統的對稱破缺解

任清褒，陳樂安，彭廣卓

（麗水學院工學院，浙江麗水323000）

0 引言

2016年，Ablowitz和Musslimani[1]引入了一個新的非局域的非線性薛定諤方程：

（1）式中*號表示復共軛，u（x，t）是變量為x，t的復值函數。與經典薛定諤方程相比較，（1）式中u*（-x，t）替代u*（x，t）。Ablowitz和Musslimani指出方程（1）是非Hermitian的，而是PT對稱的，并且是可積的。在物理學的許多領域，如量子物理[2]、光學[3]、量子場理論[4]和電路[5]等，PT對稱是十分重要的。就在最近，又利用方程（1）來描述宏觀的磁性系統[6]。

在粒子物理中，存在著一些重要的性質，如電荷共軛對稱（C）、空間對稱（Ps，x→-x+x0，x0是任意常數）、帶延遲的時間反演對稱（Td，t→-t+t0，t0是任意常數）和 PT、PC、PsC、PsTd對稱，這些性質都可以用來描述兩地的物理問題。而兩地物理問題可歸結為Alice-Bob（AB）系統[7]。因此，方程（1）可看成是一個特殊的AB系統。

本文先構建了一個特殊的AB-Benjamin-Ono（AB-BO）系統和Lax對，然后在此基礎上求得該系統的對稱破缺孤子解和對稱破缺怪波解，最后對其進行了簡單的討論和總結。

1 AB-BO系統和它的Lax對、Ba¨cklund變換、雙線性形式

我們考慮（1+1）維 Benjamin-Ono系統[8-9]：

（2）式中的β，γ分別是非線性和色散系數。在數學物理中，方程（2）是一個可積的非線性系統，用來描述深水中的內波。

根據 AB系統的原理[10]，令 u=（A+B）/2，并代入（2）式，有：

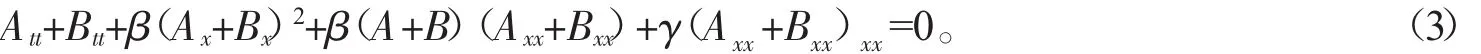
（3）式可分解為耦合方程：

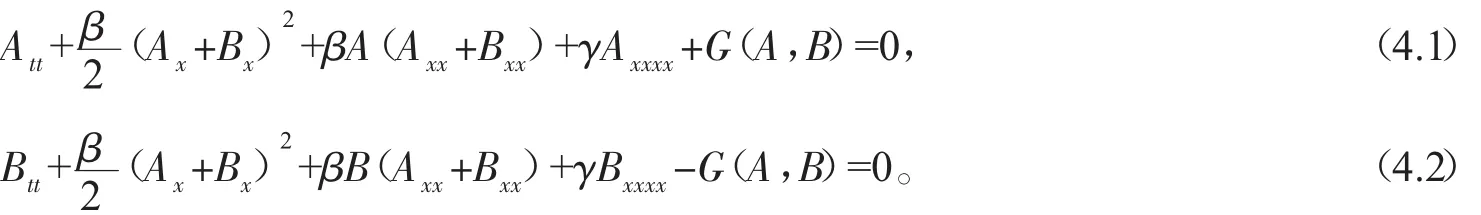
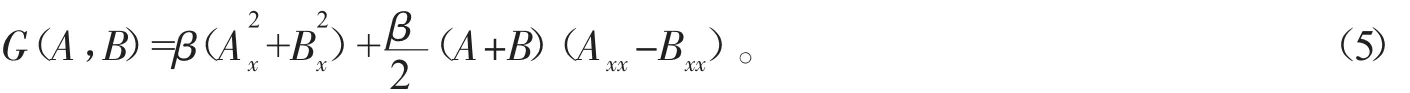
將（5）式代入（4）式，可得到下列非局域的AB-BO系統：

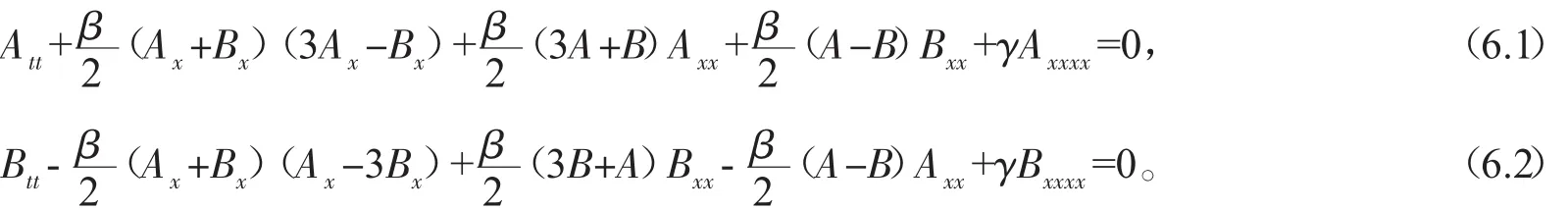
顯然，系統（6）是可積的，因為它有下列Lax對：

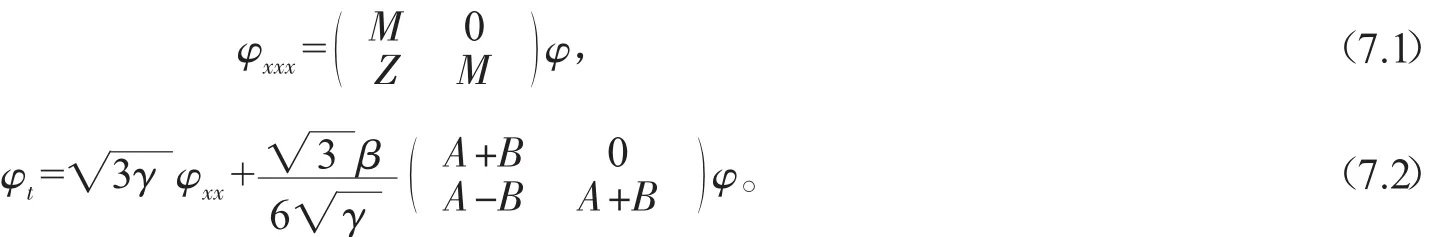
（7）式中的

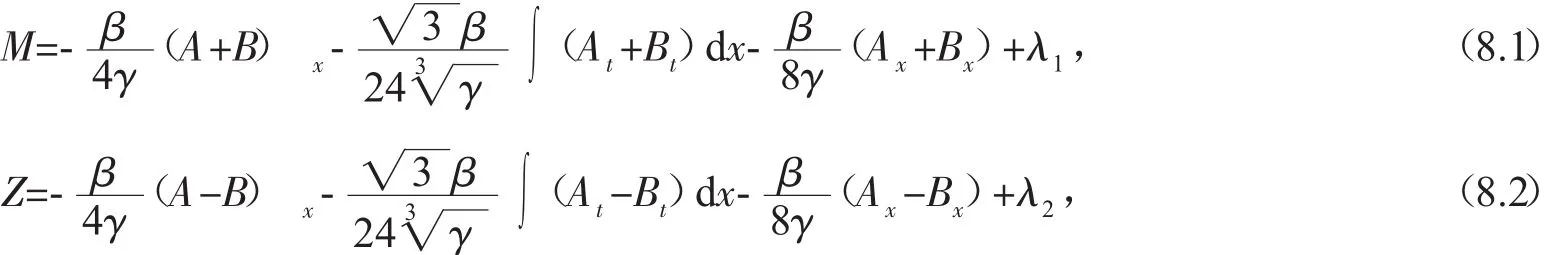
其中 λ1，λ2是任意常數。

現在引入拓展的B cklund變換:

（9）式中b1，b2，α是任意常數，F是待確定的變量為x，t的實函數，且滿足：

當b1=0，b2=0時，（9）式變為系統（1）的普通的 B cklund變換。將（9）式代入（6）式，得到AB-BO系統的雙線性形式：

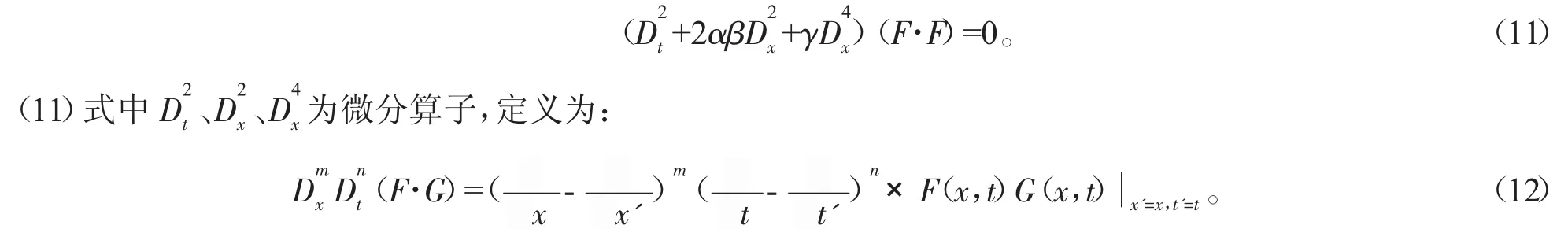
由微分算子（12）可知，方程（11）式可寫成：

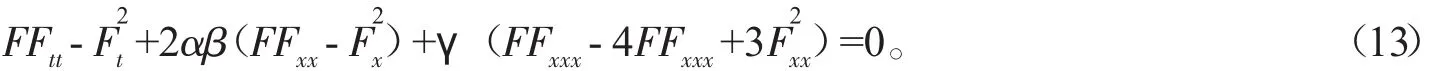
有意思的是（13）式也恰好為系統（1）的雙線性形式。

2 AB-BO系統的對稱破缺孤子解

為了獲得AB-BO系統的多孤子解，假設（13）式中的F為

式（14）中 μ 的求和應取 μi=0，1（i=1，2，…，N）的所有可能的組合，

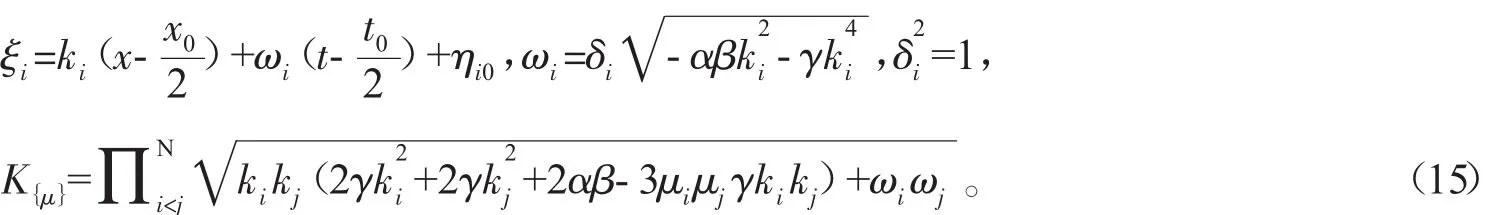
若 N=1，（14）式變為：

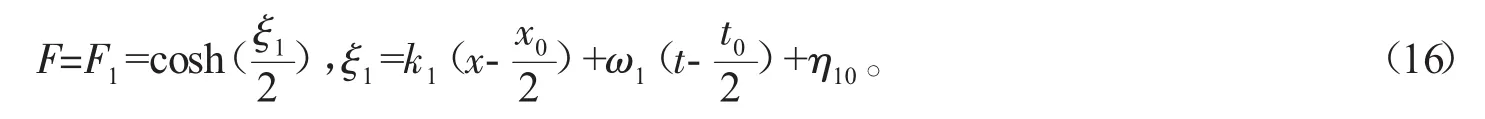
（16）式有以下兩種情形：

情形（1）：如果 η10=0，F1滿足系統的單孤子解為：

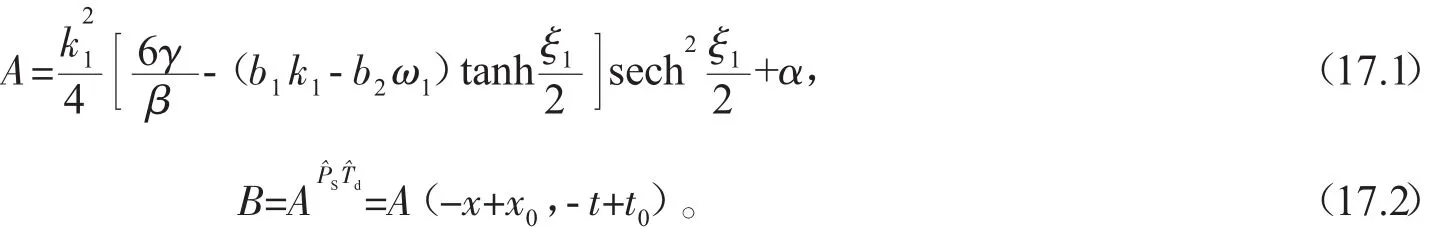
情形（2）：如果 η10、x0、t0為任意常數，F1既不能滿足下，PNAB-BO系統和TNAB-BO系統的單孤子解被禁戒。

若 N=2，（14）式變為

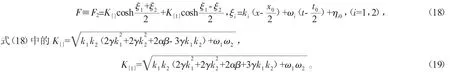
（18）式有以下兩種情形:

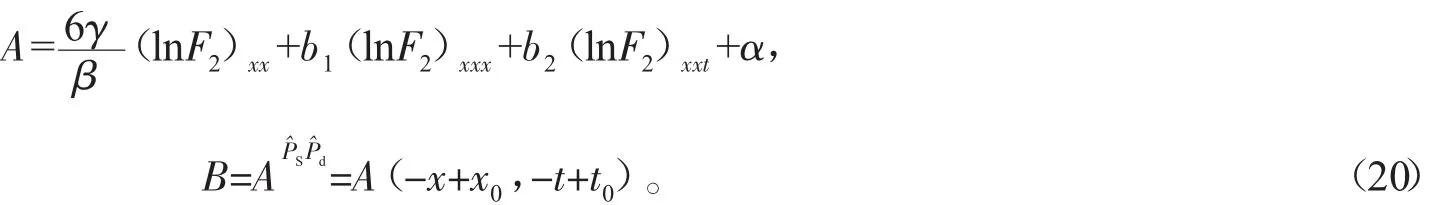
情形（2）：若

則：

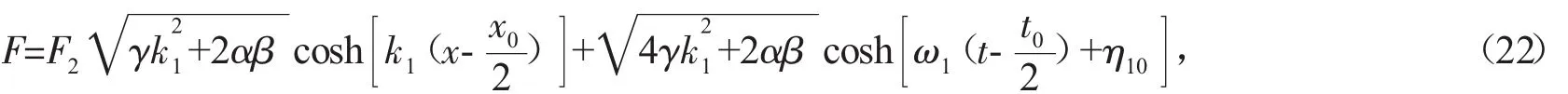
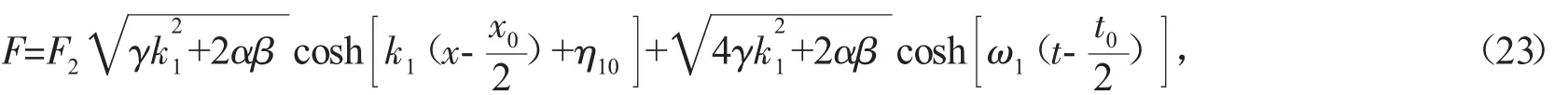
若 N=3，（14）式變為

其中

（24）式有以下兩種情形:

情形（1）：如果 η10=η20=η30=0，F3滿足，PTNAB-BO系統的雙孤子解由（9）式得到：

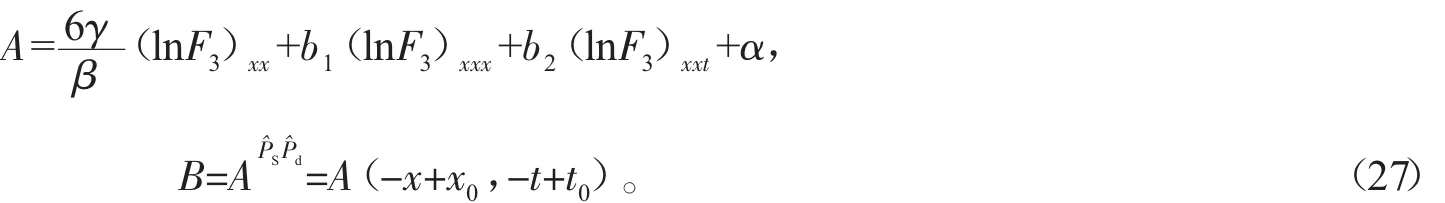
情形（2）：如果 η10、η20、η30、x0、t0為任意常數，F3既不能滿足此情形下，PNAB-BO系統和TNAB-BO系統的三孤子解被禁戒。

若 N=4，（14）式變為

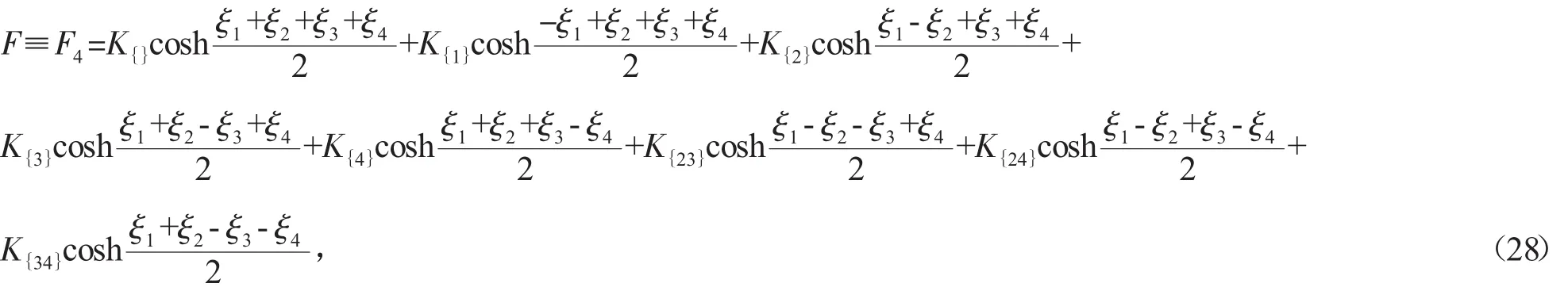
上式中的

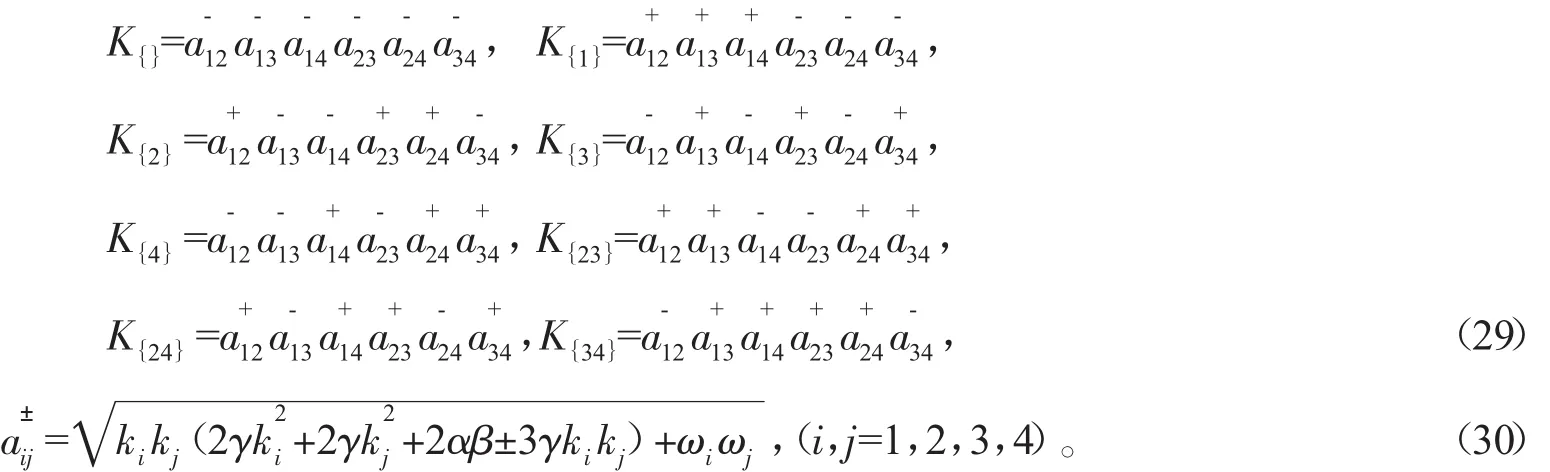
對于（28）式，有下列兩種情形:

情形（1）：如果 η10=η20=η30=η40=0，F4滿足，PTNAB-BO系統的四孤子解由（9）式得到：

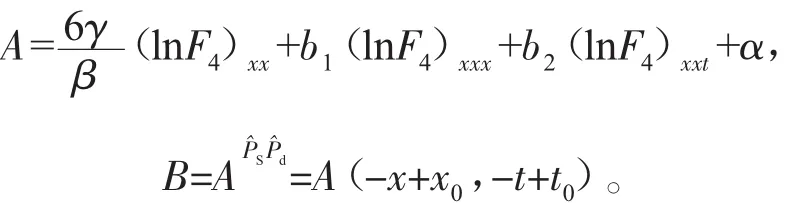
情形（2）：仔細分析后，若

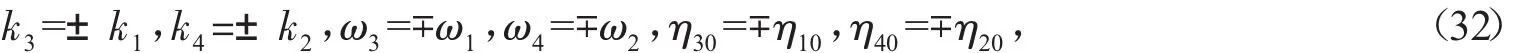
利用（33）式，容易驗證

在此情形下，對PNAB-BO系統，（28）式可重寫為:

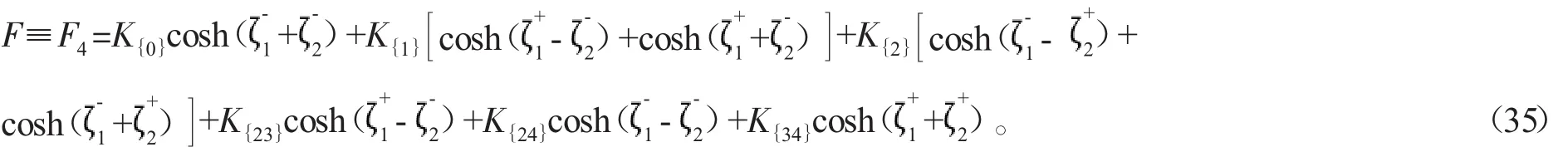
對TNAB-BO系統，（28）式可改寫成：

將（35）和（36）式代入（9）式，得到PNAB-BO系統和TNAB-BO系統的四孤子相互作用解。

3 AB-BO系統的對稱破缺的怪波解

為了得到AB-BO系統的怪波解，雙線性方程（13）式中的F具有下列形式：

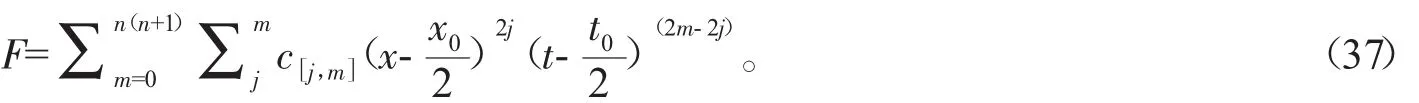
當 n=1 時，（37）式成為:

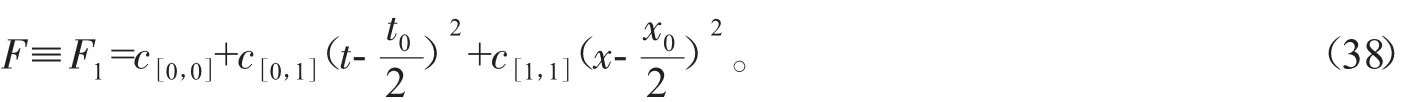
將（38）式代入（13）式，搜集有關于x，t的同次冪，令其系數為零，得到一個決定性方程組，解這一方程組，有：

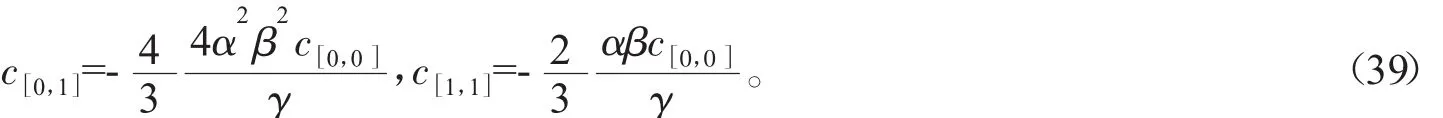
因而PTNAB-BO系統的怪波解為:

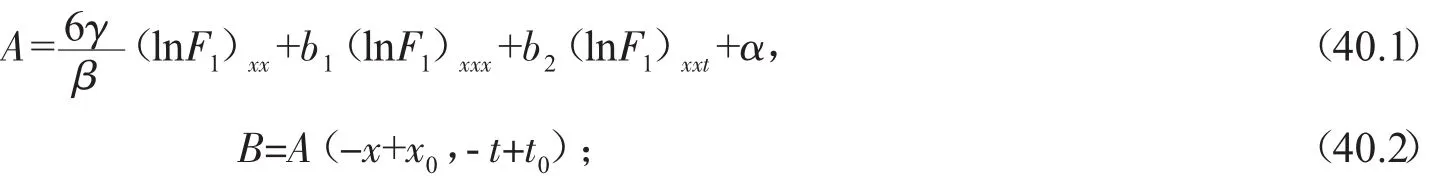
PNAB-BO系統的怪波解為:

TNAB-BO系統的怪波解為:

當 n=2 時，（37）式可寫成：

把（40）～（42）式中的F1替換為F2，即可得到AB-BO系統的二階怪波解。就高階怪波解，限于篇幅就不在此討論了。

4 總結和討論

總之，在自然界中，存在大量的兩地（AB）物理問題。研究兩地物理問題對其他科學領域有著極其深遠的影響。在這項工作中，構建了一個特殊的非局域的AB-BO系統。該系統是可積的，因為有Lax對存在。非局域的Benjamin-Ono系統奇數孤子被禁戒，顯然與局域的Benjamin-Ono系統不同。對于（5）式，是否還存在其它的形式，將有待于進一步的研究。