基于可靠度理論的輸電線路基礎設計中的風荷載調整系數取值研究

吳海洋，王松濤，葉愛民，劉 堃，白 強，曾二賢，馮 衡

(中國電力工程顧問集團中南電力設計院有限公司，湖北 武漢 430071)

0 引言

在輸電線路中，輸電塔基礎的可靠性直接決定了整個輸電系統(tǒng)的安全性及穩(wěn)定性。為適應我國電力建設發(fā)展的需要，結合可靠度理論，對基礎設計風荷載調整系數展開深入研究，具有重要意義。

將非正態(tài)隨機變量做當量正態(tài)化處理，轉化為等效正態(tài)隨機變量，然后利用改進的一次二階矩法計算結構的可靠指標即為JC法[1]。本文引進JC法進行可靠度指標計算，首先對輸電塔上部結構與地基基礎可靠度影響參數的統(tǒng)計特性及可靠度指標進行研究。計算鐵塔與基礎達到相同可靠度水平下，連接件、大板基礎抗拔下壓和樁基礎設計的風荷載調整系數取值。上述結論可為輸電線路基礎設計的安全性評價提供參考。

1 JC法簡介

1.1 當量正態(tài)化原理

設計驗算點坐標x*i(i=1，…，n)處非正態(tài)變量與其等效正態(tài)隨機變量的分布函數值以及分布密度函數值相等[2-3]，見圖1，即：

式中：θ(*)、φ(*)分別為標準正態(tài)分布函數及分布密度函數；FXi(*)、fXi(*)分別為非正態(tài)變量Xi的分布函數及分布密度函數；μ'Xi、σ'Xi分別為等效正態(tài)隨機變量Xi的均值及均方差。

利用式(1)和(2)，可求得等效正態(tài)隨機變量Xi的均值、均方差：

式中：θ-1為標準正態(tài)分布函數的反函數。

1.2 計算步驟

1)假定初始x*i(i=1，…，n)(取x*i=μXi)；

2)對非正態(tài)變量Xi，根據x*i由式(3)、(4)求等效正態(tài)變量的μ'Xi、σ'Xi，用μ'Xi、σ'Xi代替μXi、σXi；

當非正態(tài)變量Xi為對數正態(tài)分布時，利用式(5)、(6)可以計算得其等效正態(tài)隨機變量均值、均方差：

當非正態(tài)變量Xi服從極值Ⅰ型分布時，利用式(7)和式(8)可以計算得其等效正態(tài)隨機變量均值、均方差：

式中：P*為設計驗算點；Z=g(X1，…，Xn)為功能函數。

4)計算可靠度指標β

5)計算新的驗算點坐標

6)以新的驗算點坐標重復2)～5)，直到兩次計算出可靠度指標差值小于允許誤差。

2 設計表達式可靠度分析的基本原理

2.1 功能函數及變量統(tǒng)計參數

承載能力的極限狀態(tài)是指結構或構件達到最大承載力或不適合繼續(xù)承載的變形的一種狀態(tài)[4]。其功能函數表達式為：

式中：Z為功能函數；R為構件抗力，服從對數正態(tài)分布；SG和SQ分別為恒載、可變荷載(主要為風荷載)對結構構件產生的效應，分別服從正態(tài)分布和極值I型分布。各參數的均值和標準差可計算如下：

式中：μR、μR、μSG、μSQ和σR、σSG、σSQ、μSQ和σR、σSG、σSQ分別為荷載和抗力的均值和標準差；KG、KQ、KR和VG、VQ、KR分別為荷載和抗力的統(tǒng)計參數。

2.2 抗力設計表達式

1)上部結構

由DL/T 5154—2012《架空輸電線路桿塔結構設計技術規(guī)定》可知，其上部結構極限狀態(tài)設計表達式為：

其上部結構抗力標準值可確定如下：

式中：R為結構構件抗力設計值；Rk為結構構件的抗力標準值；γ0為結構重要性系數；γR為抗力分項系數；γG為永久荷載分項系數；γQ為可變荷載分項系數；SGK為永久荷載標準值；SQK為風荷載可變荷載標準值。

2)地腳螺栓

由DL/T 5154—2012《架空輸電線路桿塔結構設計技術規(guī)定》可知，其連接件抗剪極限狀態(tài)設計表達式為：

考慮輸電塔地基基礎風荷載調整系數的折減后，荷載效應標準值為：

其連接件抗剪承載力標準值可確定如下：

由DL/T5154—2012可知，其連接件抗拉極限狀態(tài)設計表達式為：

考慮輸電塔地基基礎風荷載調整系數的折減后，荷載效應標準值為：

其連接件抗拉承載力標準值可確定如下：

式中：Nv為螺栓剪切力；Nvb為受剪承載力設計值；Nc為螺栓拉力；Ncb為受拉承載力設計值；Rk為結構構件的抗力標準值；γR=2.06(根據8.8級地腳螺栓設計值與標準值之比求得)，γG為永久荷載分項系數；γQ為可變荷載分項系數；SGK為永久荷載標準值；SQK為風荷載可變荷載標準值；γw表示地基基礎相比于上部結構的風荷載調整系數折減的影響。

3)大板基礎

根據DL/T 5219—2014《架空輸電線路基礎設計技術規(guī)定》，其大板地基下壓承載力極限狀態(tài)表達式為：

上拔承載力極限狀態(tài)表達式為：

考慮輸電塔地基基礎風荷載調整系數的折減后，其大板地基的下壓承載力標準值可確定如下：

上拔承載力標準值可確定如下：

式中：SGK為永久荷載標準值；SQK為風荷載可變荷載標準值；K表示地基基礎的安全系數，應取K=2，γw表示地基基礎相比于上部結構的風荷載調整系數折減的影響。

4)樁基礎

根據DL/T 5219—2014，其樁基極限狀態(tài)表達式為：

考慮輸電塔地基基礎風荷載調整系數的折減后，荷載效應標準值為：

其樁基抗力標準值可確定如下：

式中：Rk為結構構件的抗力標準值；SGK為永久荷載標準值；SQK為可變荷載標準值；Nk為基樁的平均豎向力；R為單樁承載力特征值；γf為基礎附加分項系數，取γf=1.0；Quk為單樁豎向承載力標準值；K表示地基基礎的安全系數，取K=2；γw表示地基基礎相比于上部結構的風荷載調整系數折減的影響。

2.3 影響可靠度的因素取值

1)風荷載調整系數

本文為探討風荷載調整系數折減對輸電塔地基基礎的影響，分別對地基基礎的βz值取對塔桿0.1～1的折減，研究其對可靠度的影響，即：

式中：α取0.1～1；βz為風荷載調整系數。

2)荷載效應比

定義風荷載效應比ρW為：

因RK與SQK、SWK間存在線性關系，當SGK增大或減小時，RK也將按比例關系增大或減小。由于規(guī)范規(guī)定了γ0、γR、γG、γQ取值，若已知風荷載效應比ρW，抗力RK便可確定。在可靠度計算過程中SGK的值，通常可以假定為一個常值。若任意給定的一個效應比值ρW，即可結合JC法算出對于該效應比的可靠指標β。本文綜合現有文獻荷載效應比取值[5]，取荷載效應比為4～10。

3 荷載、抗力統(tǒng)計參數及可靠度計算流程

3.1 荷載、抗力統(tǒng)計參數

綜合考慮各文獻和相關規(guī)范，本文統(tǒng)一采用荷載重現期50 a的統(tǒng)計參數，抗力、永久荷載、可變荷載的統(tǒng)計參數取以下值。

鐵塔構件抗力R的統(tǒng)計參數：KR=1.119，VR=0.107，服從對數正態(tài)分布[6]；

地腳螺栓抗力(抗剪)R的統(tǒng)計參數：

KR=1.219，VR=0.133，服從對數正態(tài)分布[6]；

地腳螺栓抗力(抗拉)R的統(tǒng)計參數：

KR＝1.163，VR＝0.091，服從對數正態(tài)分布[6]；

大板基礎(上拔)地基抗力R的統(tǒng)計參數：KR＝1.264，VR＝0.316，服從對數正態(tài)分布[7]；

大板基礎(下壓)地基抗力R的統(tǒng)計參數：KR=1.572，VR=0.274，服從對數正態(tài)分布[8]；

樁基礎抗力R的統(tǒng)計參數：KR=1.1，VR=0.204，服從對數正態(tài)分布[9]；

永久荷載的統(tǒng)計參數：KR=1.06，VR=0.074，服從正態(tài)分布[10]；

風荷載的統(tǒng)計參數：KR=0.998，VR=0.193，服從極值I型分布[10]。

3.2 可靠度計算流程

基于上述功能函數和統(tǒng)計參數，采用JC法對上部結構、地腳螺栓和基礎進行可靠度指標計算，可靠度指標計算流程見圖2。

4 基于可靠度理論的風荷載調整系數研究

4.1 上部結構可靠度指標

采用JC法對輸電塔上部結構在不同荷載效應比下可靠度指標計算，結果見表1。

表1 鐵塔構件在不同荷載效應比下可靠度

由表1可得，輸電塔上部結構可靠度指標的平均值為3.22。

4.2 地腳螺栓(抗剪、抗拉)不同風荷載調整系數下可靠度

同樣，采用JC法對地腳螺栓(抗剪、抗拉)在不同風荷載調整系數進行可靠度指標計算，結果見表2和表3。

表2 地腳螺栓(抗剪)在不同風荷載調整系數下可靠度的平均值

表3 地腳螺栓(抗拉)在不同風荷載調整系數下可靠度的平均值

對比表2、表3與鐵塔構件可靠度指標的平均值3.22可知，地腳螺栓(抗剪、抗拉)的可靠度指標遠遠大于上部結構。

4.3 大板基礎(上拔、下壓)在不同風荷載調整系數下可靠度

同樣，采用JC法對大板基礎(上拔、下壓)在不同風荷載調整系數下可靠度進行計算，結果見表4和表5。

表4 大板基礎(上拔)在不同風荷載調整系數下可靠度的平均值

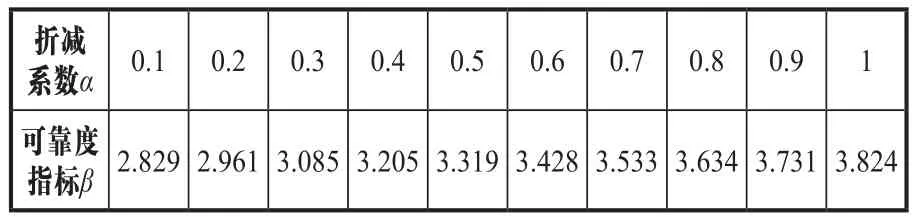
表5 大板基礎(下壓)在不同風荷載調整系數下可靠度的平均值

對比表4和表5與輸電塔上部結構可靠度指標的平均值3.22可知，當風荷載調整系數取0.4左右時，輸電塔上部結構與大板基礎的可靠度指標較為接近；當風荷載調整系數取0.5時，大板基礎的可靠度指標略大于上部結構的可靠度指標。

4.4 樁基礎在不同風荷載調整系數下可靠度

同樣，采用JC法對樁基礎在不同風荷載調整系數下可靠度進行計算，結果見表6。

表6 樁基礎在不同風荷載調整系數下可靠度的平均值

對比表6與輸電塔上部結構可靠度指標的平均值3.22可知，當風荷載調整系數取0.4左右時，輸電塔上部結構與樁基礎的可靠度指標較為接近；當風荷載調整系數取0.5時，輸電塔樁基礎的可靠度指較上部結構的可靠度指標大。

5 結論

通過對上部結構、地腳螺栓、大板基礎及樁基礎可靠度研究，可得出以下結論：

1)地腳螺栓的可靠度指標遠大于上部結構；

2)對于大板基礎(上拔)，當風荷載調整系數取0.4左右時，輸電塔上部結構與大板基礎的可靠度指標較為接近；

3)對于大板基礎(下壓)，當風荷載調整系數取0.4～0.5之間時，輸電塔上部結構與大板基礎的可靠度指標較為接近；

4)對于樁基礎，當風荷載調整系數取0.4左右時，上部結構與樁基礎的可靠度指標較為接近。