思維導圖在初中數學復習課應用的研究
徐秀婷

摘要:復習課是初中數學非常重要的一種類型課,需要對知識進行梳理和鞏固,需要在已有的基礎上發展學生的抽象思維。然而在實踐中,卻因教學形式的單一,教學手段的缺乏,很難兼顧知識網絡的搭建和思維能力的提高,不能吸引學生,教學效果差。筆者創新地在初中數學復習課中課前引入,課中探究,課堂小結三個環節有機地與思維導圖進行融合,極大地完善了學生的知識網絡,激活了學生的思維,引導學生在課堂中進一步地探究問題的本質。
關鍵詞:復習課;思維導圖;融合
中圖分類號:G633.6 ?文獻標識碼:A文章編號:1992-7711(2020)24-083
思維導圖又叫心智導圖,是一種圖形思維工具。它簡單又有效,是一種革命性的思維工具。學生借用思維導圖中的關鍵詞與圖像、顏色等快速地發現并理清知識之間的從屬關系以及層次結構,理清概念之間的聯系。同時又可以建立知識的結構體系,幫助學生從整體上去把握知識之間的內在邏輯關系。并可以有效調用左右腦去進行知識的記憶、理解和運用,促進思維的發展。
復習課對于學生知識的鞏固與梳理,融會與貫通有著重要的作用。雖然有學者對復習課給出這樣的建議:首先教師要做好學生分析,找準學生的最近發展區域;其次要設置好問題鏈,給學生搭建好腳手架;最后拾級而上,關注學生的層層遞進。然而在現實中,復習課只是知識的簡單累積和重復,優生不想聽,學困生似懂非懂,往往一場精心準備的復習課,最后草草結束,掃興收場。因此在復習課中,不僅要鞏固一章節的知識,同時還要探討到知識以外的活動經驗和思想方法。因此筆者創新地在課前引入,課中探究,課后總結這三個環節與思維導圖進行了融合。下面將以銳角三角函數初三這節復習課為例,來探討思維導圖與數學復習課的融合。
一、巧用導圖進行課前回顧搭建知識結構框架
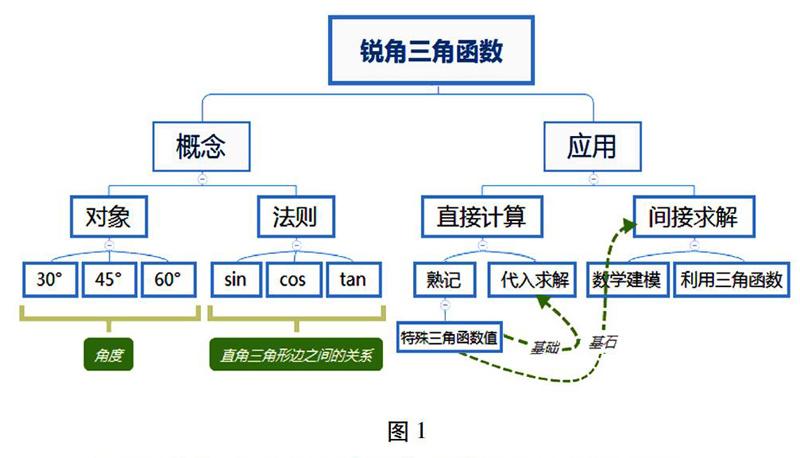
銳角三角函數的復習課的教學目的,不僅要幫助學生掌握有關銳角三角函數的基本知識,基本技能,還需要學生通過探究去提高解題的基本數學思維和方法,積累相應的解題經驗。而知識是載體,是根本,如何快速地激活學生已有的知識結構,關注到每一位學生是這節課的關鍵點。筆者通過“概念”、“應用”一級分類關鍵詞,幫助學生主動、快速地在大腦之中對知識進行有序分類和組合;通過“概念”之下的“對象”、“法則”以及“應用”之下的“直接計算”,“間接求解”等二級分類關鍵詞,幫助學生迅速回顧,輸出相應的基本知識,并搭建相應的知識結構;通過二級分類關鍵詞下面的一層三級關鍵詞,幫助學生搭建相應的知識網絡,如圖1。
學生在通過課前導圖知識圖片化的回顧下,在完善自身的知識結構體系外,還進一步理清銳角三角函數“是什么”的問題,以及銳角三角函數“有什么用”的問題。同時在導圖的指引和教師的啟發下,學生可以思考,角度難道一定是一成不變的,只能取特殊值?它可以變化嗎?甚至可以引出當角度變為非特殊角時,需要添加什么條件,才能解決問題,從而促進學生思辨思維的發展。同時通過導圖,學生不難發現基本的特殊三角函數值是所有應用的基礎,而特殊三角函數的值,是根據三角函數的定義、概念而來的。只有深刻理解三角函數概念的價值,才會引起學生的重視,間接促使學生的靈活運用,從而讓許多問題迎刃而解。
二、活用導圖課中適時歸納促進學生探尋問題本質
學生在進行解題的時候,思維往往充滿局限性,通常表現在對問題的認識只是局限在問題的表面,不善于聯系和聯想,不善于知識的遷移和組合。因此在復習課上,要及時地對研究的問題進行歸納,幫助學生認清問題的本質。筆者在這節銳角三角函數的復習課中, 設計了如下探究題:
在 RT△ABC中,∠C=90°,AB=10,cosB=35。
1.求sinB,tanA的值。
2.上題中AB=10的條件可以去掉嗎?sinB,tanA的值改變嗎?
設計意圖:第一問考查學生對銳角三角函數概念的理解和靈活應用,樹立學生可以解決問題的信心,又為下一問的沖突做好鋪墊。第二問中是否可去掉條件AB=10的這個問題,從條件變化的角度,去引發學生的思考,從直觀感覺不可以,到經過嚴密的邏輯推理又可以的一個轉變,培養學生思維的邏輯性和嚴謹性。
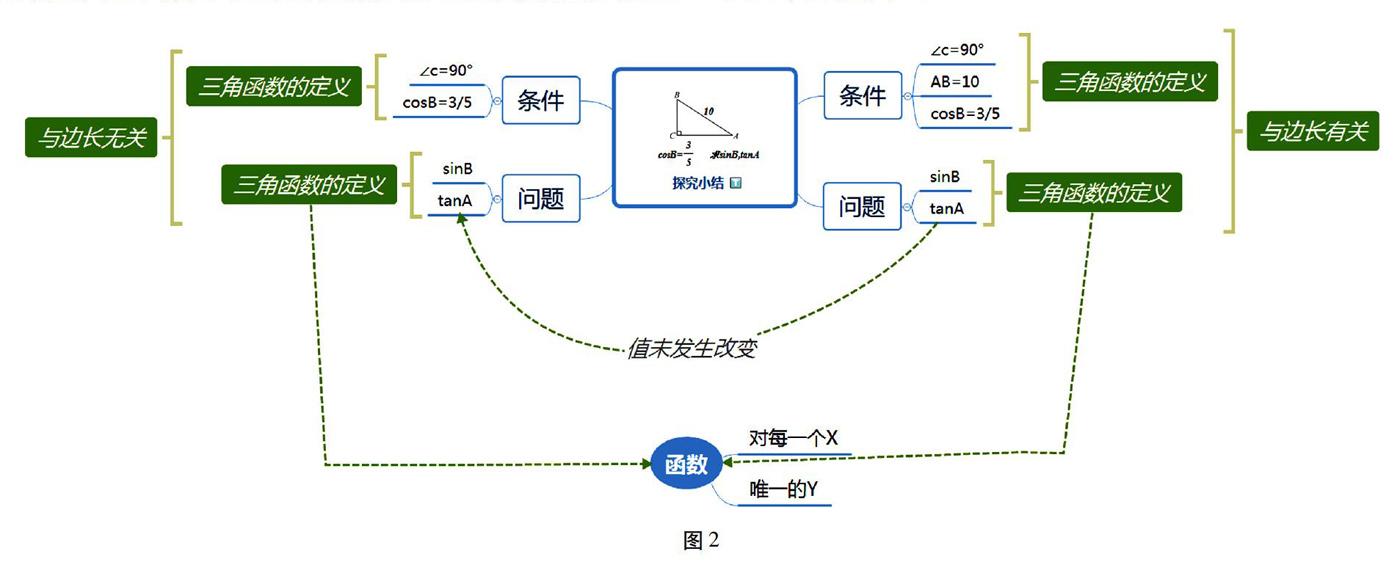
解決手段:首先筆者通過引導學生反省第一問的成功解題過程,分離出問題條件和問題本身,抽離出解題過程隱藏的關鍵元素,并用導圖畫出。其次采用第一問的方法,分離出條件和問題本身,抽離出隱藏的關鍵元素,然后進行對比,尋找不同點,直追問題本質,如圖2。
學生反饋:通過可視化后思維的對比,學生明白此問題的本質是三角函數的值是否與邊長有關的問題?因此只要回歸到函數這個定義,就不難發現三角函數值只與角度有關,而給定邊長的長度,只不過借助具體的數量去幫助學生理解和計算。在直角三角形中,給定一個三角函數和它的值,就能找到三角形三邊的比例關系,與長短無關,甚至可以由此進一步強化銳角三角函數與相似三角形之間的關系, 從而進一步培養學生的科學研究問題的方法,和對學生邏輯思維能力的培養。
三、基于導圖課堂小結 促進章節之間的融合,完善知識網絡結構
課堂小結作為課堂教學的重要組成部分,已被大部分教師認可和接受。但是普遍教師采用的方法是:自我評價法,概括總結法,問題小結法,提煉深化法等其中的一種或者幾種的組合。而學生通過小結,更多的只是鞏固所學的本章節的知識,很少會涉及到與其它章節知識之間的融合。
思維導圖因其與大腦里的神經元細胞結構非常相似,它為許多可能提供了空間。因此在課堂小結的時候,借助導圖的思維可視化,讓學生感悟出,即使是任意一個三角形,只要滿足一定的條件,就可以把邊長與角求出來。如給出的條件是兩角一邊,就可以求出另外的角和邊。因為無論是特殊角還是一般角都屬于角,讓學生意識到解決這類問題只需要進行方法的遷移,同時在小結時,通過導圖,以并列關系呈現出任意三角形和特殊三角形的關系,可以充分地刺激學生大腦。讓學生主動通過輔助線去建立一般與特殊之間的關系,巧妙地進行專注思維和發散思維的切換。降低了學習難度,提升學習數學興趣。甚至我們可以利用導圖的空白部分,去發散學生的思維,建立與其它章節之間的聯系。如求銳角三角函數的值跟三角形全等的條件是否相關,條件是否可以轉化為邊角邊,進而引導學生發現問題和提出問題,除了三角形,還有跟哪些知識點可以融合在一起?引導學生主動回憶,聯系和聯想,把課堂小結推向高潮如圖3。基于導圖的知識小結,在促進學生發散思維,創新思維培養的同時,促進不同章節之間的融合,有效地完善了學生的已有知識網絡。
綜上所述,在復習課中與思維導圖的有效融合運用,不僅重構了知識體系,訓練了學生的思維,還有效地激發學生自主探究的欲望。
參考文獻:
[1]劉曉波.“斗圖+思維導圖”突破七年級應用題教學難點的實踐研究[J].2020.
[2]袁丹丹,蔡小雄.拾級而上 ?順藤摸瓜——以“函數零點問題”為例談數學復習課[J].教學月刊·中學版(教學參考),2014(19):55-57.
【本文系2017年中央電化教育館全國教育信息技術研究規劃課題“巧用思維導圖,實現中學數學高效課堂的教學模式研究”(立項號:174430052)的階段成果之一。】
(作者單位:中山市東區松苑中學,廣東 中山 528400)

