考慮樁側初始剪應力的層狀地基中單樁沉降計算簡化解析

劉曉華，韋彬，張鵬鵬，趙煉恒

考慮樁側初始剪應力的層狀地基中單樁沉降計算簡化解析

劉曉華1，韋彬1，張鵬鵬2，趙煉恒2

(1. 深圳市綜合交通設計研究院，廣東 深圳 518003；2.中南大學 土木工程學院，湖南 長沙 410075)

針對現有側阻雙曲線模型參數計算較困難的問題，提出一種考慮樁側土初始剪應力以及側阻軟化特性的簡化側阻三折線模型；并結合樁端位移與樁端承載力的非線性發揮關系，采用雙曲線模型模擬樁端荷載傳遞性狀。進一步在上述樁側和樁端荷載傳遞模型基礎上，提出一種獲取單樁荷載-沉降關系的簡化遞推分析方法。實例分析表明，本文所提簡化模型與計算方法應用于單樁沉降計算具有較好的精度，且分析模型參數獲取容易、計算便捷，研究成果可為設計施工提供有益參考。

單樁沉降；初始剪應力；三折線模型；層狀地基；數值模擬

單樁沉降計算方法目前主要有5種[1?4]：1) 簡化計算法，通過計算樁頂軸向剛度系數獲得軸向荷載下樁頂位移；2) 剪切位移法，假定樁的沉降主要來自于樁周土的環形剪切變形，從而通過計算樁周土的剪切位移來計算單樁沉降；3) 彈性理論法，將土體視為線彈性體，并假定樁土之間無相對位移，土體的特性僅由彈性模量和泊松比來反映，通過彈性理論計算樁土的應力狀態；4) 有限元法，該法利用數值計算軟件進行建模計算，可以考慮實際三維效應；5) 荷載傳遞法，通過建立樁?土間的荷載傳遞函數來分析樁?土相互作用。荷載傳遞法可根據不同的地層條件選用或修改荷載傳遞函數，其適應性好、計算簡單，可應用于均質地基和成層地基中單樁沉降分析，該方法的關鍵即在于建立合適的樁側和樁端荷載傳遞模型。目前，樁側荷載傳遞模型主要有理想彈塑性模型、雙折線模型和雙曲線模型，其中側阻雙曲線模型[5]能較好地反映樁側土界面荷載傳遞形狀而應用最為廣泛。張乾青等[5]基于現場試樁試驗數據擬合出一種側阻軟化雙曲線模型，其具有較好的試驗依據且適應性良好；趙明華等[6]根據土與混凝土直剪試驗[7]結果提出一種考慮初始臨界側阻的簡化雙曲線模型；賀志軍等[8]則在現有雙曲線模型基礎之上，提出一種同時考慮初始極限剪應力和側阻軟化效應的分段雙曲線模型。對于樁端荷載傳遞特性采用端阻雙曲線模型即能較好地描述其荷載?位移關系。現有研究表明，側阻軟化雙曲線模型未考慮低荷載水平下樁?土界面初始臨界側阻的存在，簡化雙曲線模型未能考慮高荷載水平下的側阻軟化效應，故以上2種側阻雙曲線模型的適應性有待提高；而分段雙曲線模型雖能同時考慮初始側阻和應變軟化效應，但其荷載傳遞函數較為復雜，且引入的參數需要求解復雜方程才能得到，難以快速應用于工程實踐中。因此本文在側阻雙曲線模型基礎上，提出一種同時考慮初始極限剪應力和側阻軟化效應的三折線模型；該模型參數獲取容易，計算過程簡單且速度較快。并在此模型基礎之上采用一種簡化遞推方法計算單樁沉降。

1 樁?土荷載傳遞模型

1.1 荷載傳遞法基本思想

把樁沿樁長方向離散，每段單元體通過非線性彈簧將剪切荷載傳遞至樁側土，此非線性彈簧的應力應變關系即為該深度處樁側摩擦阻力()與樁土相對剪切位移()之間的關系；同理，樁端土也通過樁端非線性彈簧與土體相連，該彈簧的應力應變關系則代表樁端阻力Q與樁端位移S之間的關系，此關系即為荷載傳遞函數。其計算簡圖如圖1所示。

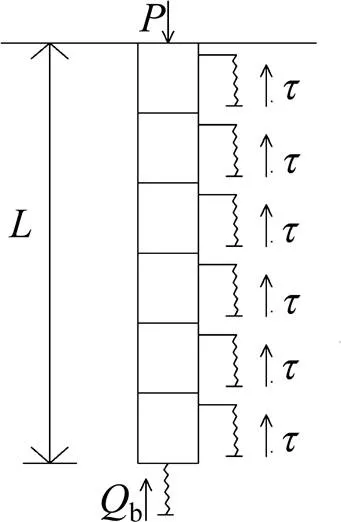
圖1 荷載傳遞法計算簡圖

樁?土荷載?位移關系的基本微分方程：

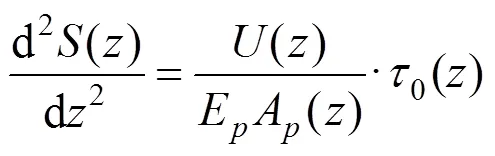
求解微分方程(1)中側阻函數的方法有2種： 1) 通過現場實測數據擬合；2) 根據一定的經驗結合地基土物理力學機理分析，得到具有廣泛適用性的理論傳遞函數。

1.2 樁側荷載傳遞模型

1.2.1 側阻軟化雙曲線模型

側阻雙曲線模型[5]的數學表達式為：

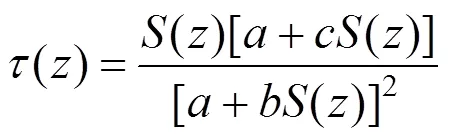
式中：()為樁側摩阻力；()為深度處樁土相對位移；，和均為參數，其表達式分別為[5]：

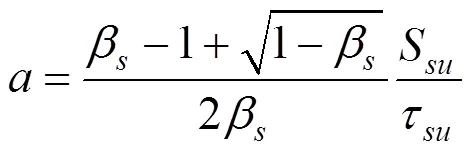
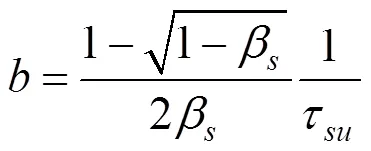
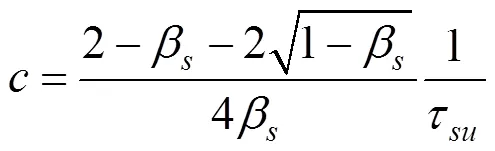
式中：β為側阻破壞比，等于殘余側阻力/極限側阻力；S為極限側阻對應的樁土相對位移。

1.2.2 本文提出的改進模型

雙曲線模型中側阻?相對位移函數較為復雜，且需要解方程以獲取模型參數。側阻雙折線模型計算形式較簡單、計算參數較少，也可描述樁?土間的非線性關系，但未考慮極限側阻與極限相對位移，故當荷載水平較大時將出現較大偏差。因此本文在雙曲線模型的基礎上對其進行簡化，同時考慮初始極限剪應力與側阻應變軟化效應的存在，提出一種考慮初始剪應力的側阻軟化三折線模型，其計算形式簡單、計算參數較易獲得，且與雙曲線模型較為接近，也能保證足夠的精度。

如圖3所示，在側摩阻力小于初始摩阻力0時，在樁土界面不會有相對位移；側摩阻力大于初始摩阻力0，側摩阻力會隨著相對位移線性增加，直至最大值極限摩阻力max，此時樁土位移為S1；此后側摩阻力會隨著相對位移增大而減小，直到位移達到S2，此時側摩阻力到達殘余側阻τ。

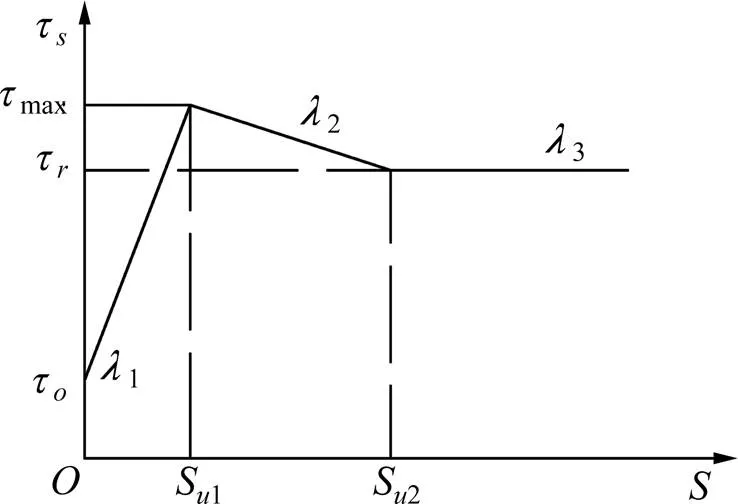
圖3 三折線側阻與位移之間的關系

樁土界面側摩阻力與位移之間的關系式如下：

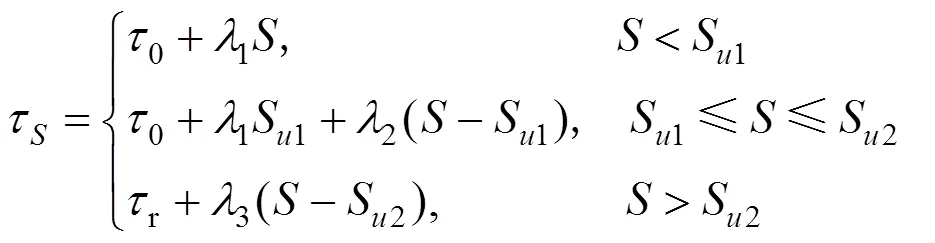
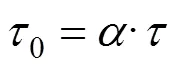
以上參數可通過現場實測數據反分析獲得，可根據經驗取值。其中，張乾青等[5]對現場實測數據統計表明，不同土層中極限側摩阻力對應的極限樁土相對位移(彈性界限相對位移S1=5~25 mm)；殘余摩阻力與極限摩阻力的比值約為0.93~0.97。且1，2和3為側阻函數不同發揮階段的斜率：

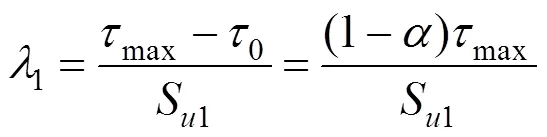
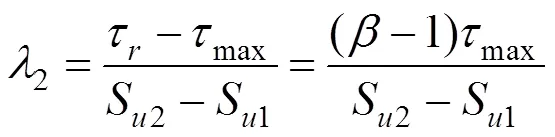
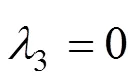
1.3 樁端荷載傳遞模型

如圖4所示，樁端雙曲線模型數學表達式為：

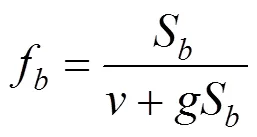
式中：v和g為參數；Sb是樁端位移；fb是樁端 阻值。

1.3.1 參數的確定

當S=0時，對式(10)求導得到：

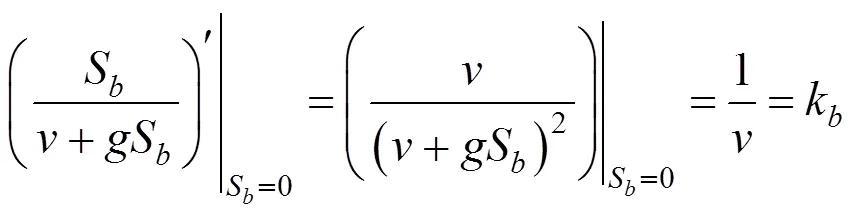
樁端土彈簧剛度由Randolph等[9]給出：

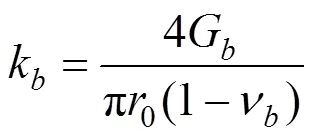
式中：G與v分別表示樁端土剪切模量與泊松比。

聯立式(11)和(12)可得：

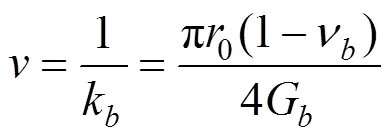
1.3.2 參數的確定

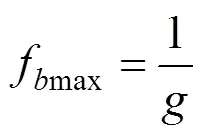
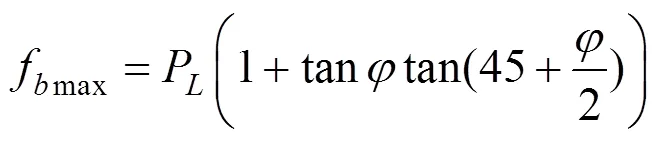
式中：P為球孔極限應力；為內摩擦角，該參數值由下式得到：

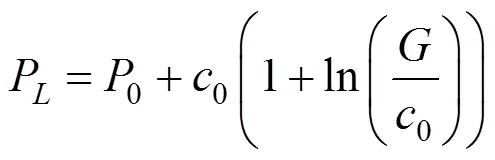
式中：0為黏聚力；0為對應深度處原位土應力。

最后聯立式(14~16)即可得到參數。

2 沉降求解方法

假設樁長為，彈性模量為，樁周長為；將樁沿著長度方向離散為個單元，單元長度為，且=/。給定一個樁端位移S，通過樁端模型可以得到一個樁端載荷Q。

1) 分析底部單元。假定一個較小的樁端位移S，由式(10)得到樁端力，Q根據本文提出的考慮初始剪應力的三折線模型，即可得到樁側摩阻力。單元體受到樁端阻力Q，樁側阻力，軸力在這3種力作用下平衡。得到平衡方程：

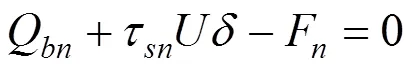
易得軸力：

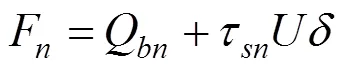
單元體壓縮量：

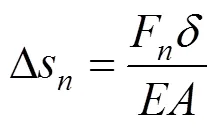
單元體上表面沉降量：

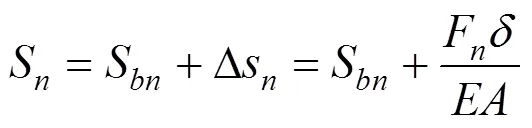
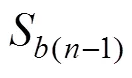
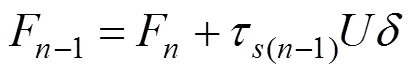
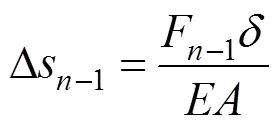
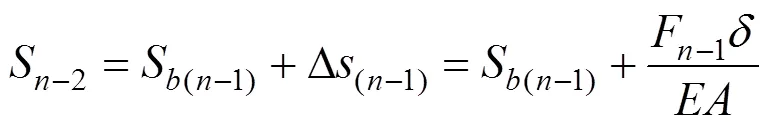
重復上述計算步驟，最終可得樁頂單元上表面的力0，即樁頂荷載；同時可得到上表面的位移0，即樁頂沉降。計算步驟如下：

①將樁分為個單元；

②給定一個較小的樁端位移S；

③根據樁端位移S和式(10)得到樁端荷載Q；

④假定樁段中心位移S等于樁端端位移S，代入式(6)得到樁段側阻；

⑤由式(18)計算得到樁段的頂部荷載F；

⑥由式(19)得到樁段壓縮量Ds；

⑦由式(20)得到樁段頂部沉降S?1；

⑨重復步驟④~⑧。即可得到多組樁頂荷載和樁頂沉降值。

3 算例驗證

茅草街大橋為一座特大型鋼管混凝土拱橋，位于湖南省南縣茅草街鎮，其樁基礎為鉆孔灌注 樁[17]。某試樁樁徑1 m，樁長60 m，采用C30混凝土，實測混凝土彈性模量為3.47×104MPa。試樁樁周土體物理力學指標如表1所示。

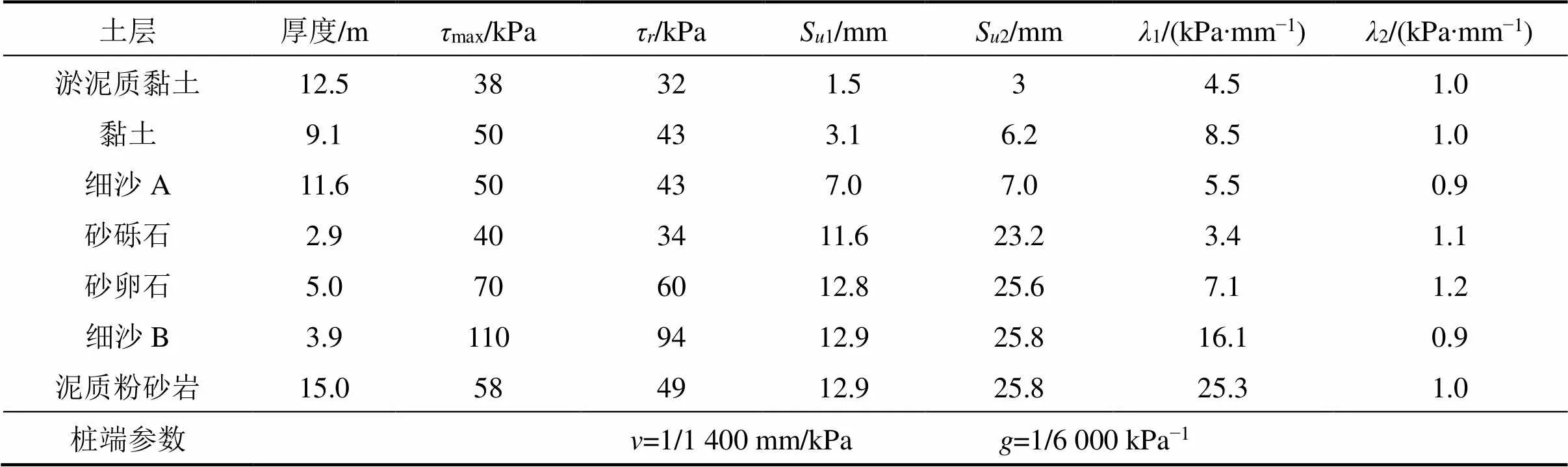
表1 茅草街大橋地基土物理力學性質參數

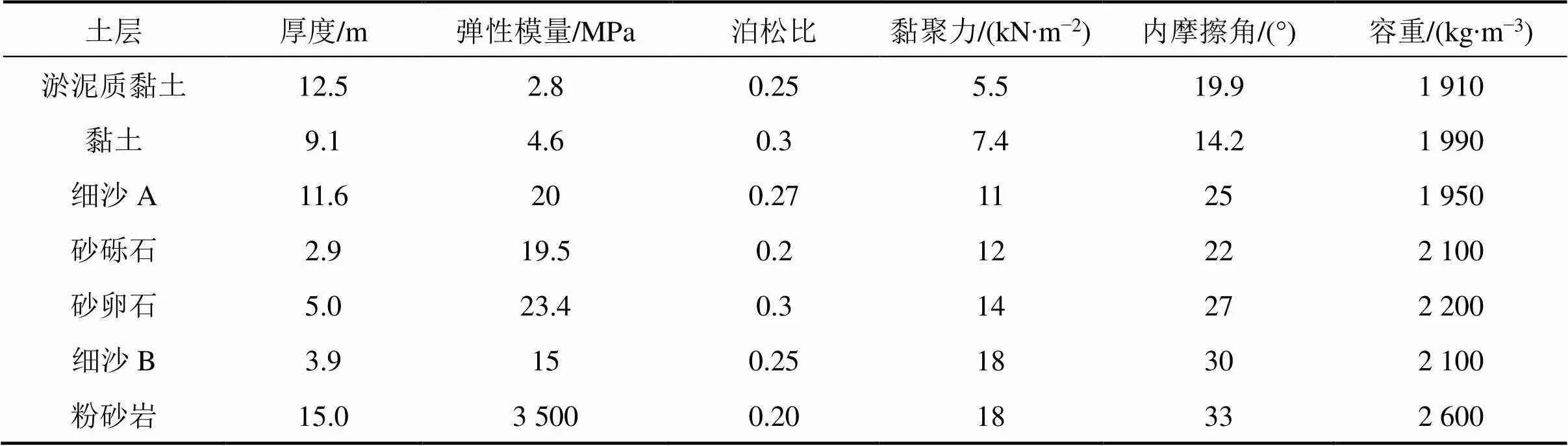
表2 土體參數(Morh-Coulomb模型)

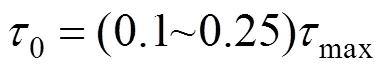
為進一步驗證本文模型與計算方法的合理性，應用有限元軟件ABAQUS對上述算例進行建模分析。建模分析過程中，模型空間為二維平面，樁側土與樁下土均取20倍樁徑；樁的本構模型為線彈性均質模型，選用摩爾庫倫模型模擬土的本構模型，土體參數見表2；樁側土界面接觸方式設置為面面接觸，其切向行為與法向行為分別定義為罰函數與硬接觸，樁端與樁端土連接為綁定約束。

如圖5所示，基于本文提出的側阻三折線模型及簡化遞推方法計算所得的荷載?沉降曲線與實測荷載?沉降值擬合較好。由三折線模型計算所得的沉降曲線與由雙曲線模型和數值模擬計算所得的沉降曲線相比，數值模擬計算所得的沉降曲線與實測沉降曲線擬合最好，由三折線模型計算所得的沉降曲線精度次之；由雙曲線模型計算得的沉降曲線與由三折線模型計算結果總體較為接近，當荷載小于 11 000 kN時，由本文三折線模型計算所得的沉降曲線與實測值擬合更好，表明本文所提的側阻三折線模型因考慮了初始極限剪應力的存在而使得當樁頂荷載水平較低時與實際側阻發揮情況更為接近。

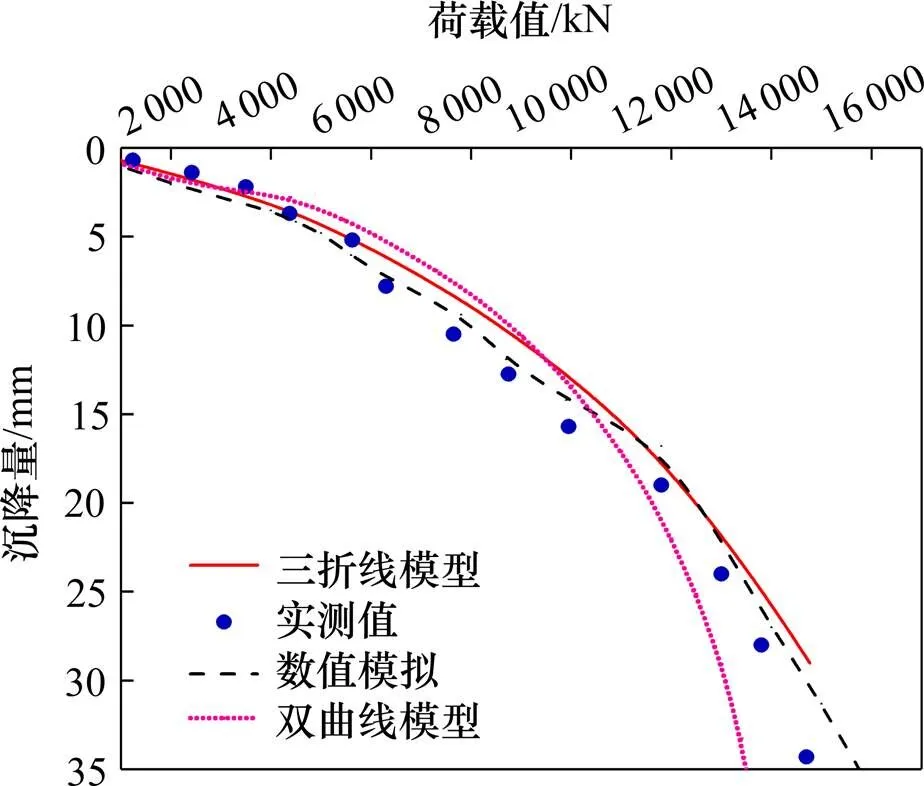
圖 5 荷載?沉降曲線對比

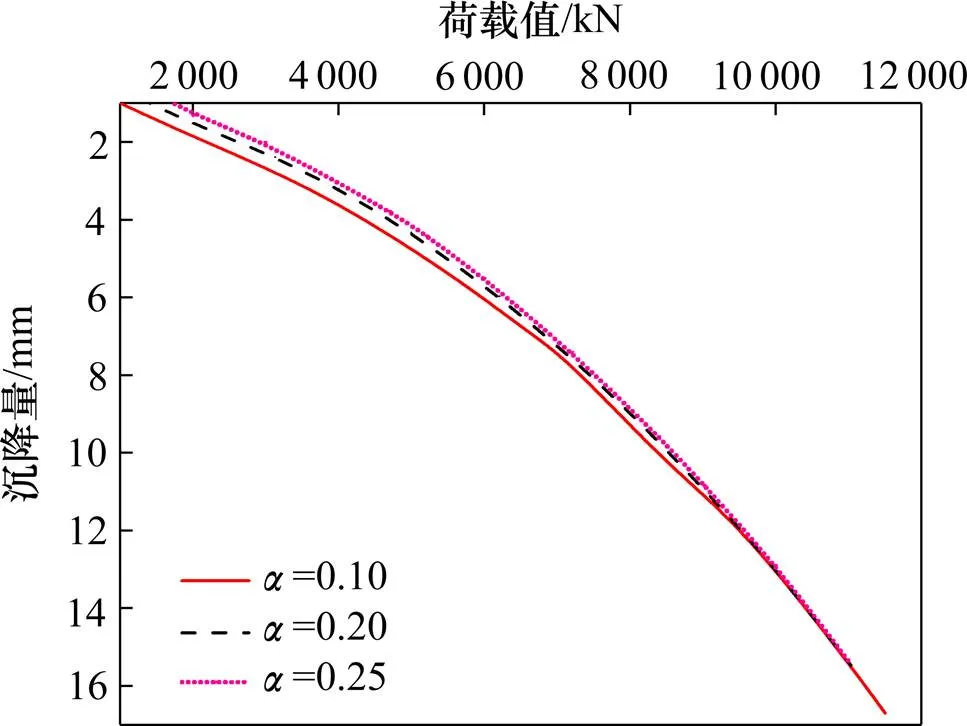
圖6 參數α對荷載?沉降的影響

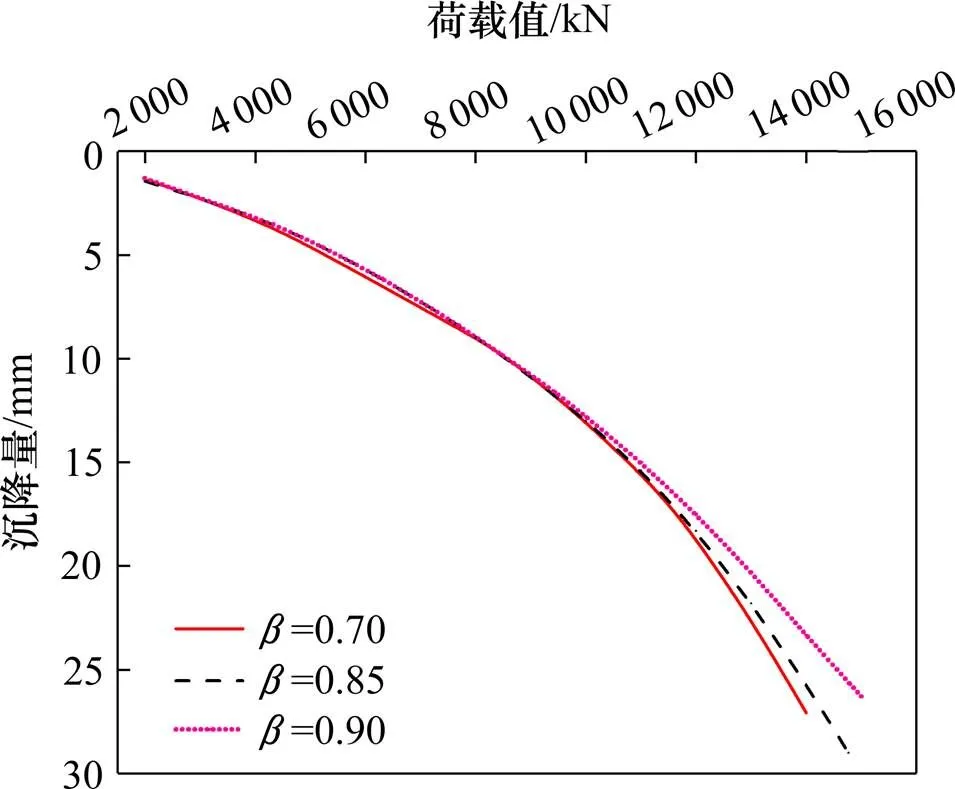
圖7 參數β對荷載?沉降的影響

圖6表明，參數在荷載較小時對荷載?沉降曲線影響較大，初始剪應力越大，低荷載水平時單樁承載力略有增大；當單樁樁頂荷載足夠小時，樁?土界面因初始剪應力的存在而未發生滑移，導致出現沉降為0荷載卻不為0的情況，但實際情況中由于樁側土的剪切變形在荷載較小時也會出現沉降。圖7表明，參數在荷載較大時對荷載?沉降曲線影響較大，即高荷載水平作用下側阻才出現軟化效應，也即側阻軟化效應當樁頂荷載較大時體現得更明顯，故圖7中各條曲線在10 000 kN之后才出現差異(越大，高荷載水平下沉降速率越大)。

4 結論

1) 基于樁側雙曲線模型，提出了一種同時考慮初始剪應力和應力軟化特性的側阻三折線模型，并利用一種簡化遞推方法，對單樁沉降特性進行了分析，可獲得單樁荷載?沉降曲線。

2) 算例分析表明，基于本文提出的考慮初始剪應力的側阻軟化三折線模型和簡化遞推方法，能夠較準確地計算出單樁沉降，且計算結果與基于雙曲線模型的計算結果和數值模擬計算結果較接近，可到達較高精度，且本文計算過程更為簡單。

3) 參數分析表明，參數對低荷載水平下單樁荷載?沉降特性有一定影響，參數對高荷載水平下單樁荷載?沉降特性影響較大，當越大、越小時，單樁承載力越高。

[1] Cooke R W, Price, G. Strains and displacements around friction piles[C]. Proc 8th ICSMFE, Moscow, 1973, 2: 53?60.

[2] Poulos H G, Davis E H. Pile foundation analysis and design[M]. New York: John Wiley and Sons, 1980.

[3] Comodromos E M, Papadopoulou M C, Rentzeperis I K. Pile foundation analysis and design using experimental data and 3-D numerical analysis[J]. Computers & Geotechnics, 2009, 36(5): 819?836.

[4] Kraft L M, Ray R P, Kagawa. Theoretical T-Z curves[J]. International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts, 1982, 11(107): 1543?1561.

[5] 張乾青, 李連祥, 李術才, 等. 成層土中單樁受力性狀簡化算法[J]. 巖石力學與工程學報, 2012, 31(增1): 3390?3394. ZHANG Qianqing, LI Lianxiang, LI Shucai, et al. Simplified algorithm of single pile behavior in layered soil[J]. Journal of Rock Mechanics and Engineering, 2012, 31(Suppl 1): 3390?3394

[6] 趙明華, 劉蘇, 尹平保, 等. 考慮樁土界面初始臨界摩阻力影響的基樁沉降計算方法[J]. 中南大學學報(自然科學版), 2013, 44(8): 3425?3431. ZHAO Minghua, LIU Su, YIN Pingbao, et al. Calculation method of pile settlement considering the influence of initial critical friction of pile-soil interface[J]. Journal of Central South University (Natural Science Edition), 2013, 44(8): 3425?3431.

[7] 殷宗澤, 朱泓, 許國華. 土與結構材料接觸面的變形及其數學模擬[J]. 巖土工程學報, 1994(3): 14?22. YIN Zongze, ZHU Hong, XU Guohua. Numerical simulation of the deformation in the interface between soil and structural material[J]. Chinese Journal of Geotechnical Engineering, 1994, 16(3): 14?22.

[8] 賀志軍, 雷皓程, 夏張琦, 等. 多層軟土地基中單樁沉降與內力位移分析[J]. 巖土力學, 2020, 41(2): 1?16. HE Zhijun, LEI Haocheng, XIA Zhangqi, et al. Analysis of settlement and internal force displacement of single pile in multilayer soft soil foundation[J]. Rock and Soil Mechanics, 2020, 41(2): 1?16.

[9] Randolph M F, Wroth C P. An analysis of the vertical deformation of pile groups[J]. Geotechnique, 1979, 29(4): 423?439.

[10] 劉俊龍. 用標貫擊數估算單樁極限承載力[J]. 巖土工程技術，2000, 3(2): 88?91. LIU Junlong. Estimation of ultimate bearing capacity of single pile by SPT blow count[J]. Geotechnical Engineering Technology, 2000, 3(2): 88?91.

[11] 李家奇，趙曉豹，李曉昭, 等. 不同地區砂土中樁端承載力計算方法的比較[J]. 地下空間與工程學報, 2009, 5(5): 1007?1012. LI Jiaqi, ZHAO Xiaobao, LI Xiaozhao, et al. Comparison of calculation methods for bearing capacity of pile tip in sandy soil in different areas[J]. Journal of Underground Space and Engineering, 2009, 5(5): 1007?1012.

[12] 魏杰. 靜力觸探確定樁承載力的理論方法[J]. 巖土工程學報, 1994, 16(3): 103?111. WEI Jie. Theoretical method of determining the bearing capacity of pile by static penetration test[J]. Journal of Geotechnical Engineering, 1994(3): 103?111.

[13] 趙春風, 蔣東海, 崔海勇. 單樁極限承載力的靜力觸探估算法研究[J]. 巖土力學, 2003, 24(增2): 408?410. ZHAO Chunfeng, JIANG Donghai, CUI Haiyong. Study on the estimation method of the ultimate bearing capacity of single pile by static penetration test[J]. Geotechnical Mechanics, 2003(Suppl 2): 408?410

[14] JGJ94—2008, 建筑樁基技術規范[S]. JGJ94—2008, Technical code for building pile foundation[S].

[15] JTG D63—2007, 公路橋涵地基與基礎設計規范[S]. JTG D63—2007, Code for design of subgrade and foundation of highway bridge and culvert[S].

[16] Randolph M F. Science and empiricism in pile foundation design[J]. Geotechnique, 2003, 53(10): 847?875.

[17] 趙明華, 鄒新軍, 劉齊建. 洞庭湖軟土地區大直徑超長灌注樁豎向承載力試驗研究[J]. 土木工程學報, 2004, 37(10): 63?67. ZHAO Minghua, ZOU Xinjun, LIU Qijian. Experimental study on vertical bearing capacity of large diameter and super long cast-in-place pile in Dongting Lake soft soil area[J]. Journal of Civil Engineering, 2004 37(10): 63?67

[18] 崔廣芹. 基于現場單樁載荷試驗結果的樁土參數識別方法[D]. 西安: 西安建筑科技大學, 2011. CUI Guangqin. Identification method of pile-soil parameters based on the results of field single pile load test[D]. Xi’an: Xi’an University of Architecture and Technology, 2011.

[19] 張乾青, 李術才, 李利平, 等. 考慮側阻軟化和端阻硬化的群樁沉降簡化算法[J]. 巖石力學與工程學報, 2013, 32(3): 615?624. ZHANG Qianqing, LI Shucai, LI Liping, et al. Simplified settlement algorithm of pile group considering lateral resistance softening and end resistance hardening[J]. Journal of Rock Mechanics and Engineering, 2013, 32(3): 615?624.

Simplified analytical for settlement calculation of single pile in layered soil considering initial shear stress of pile side

LIU Xiaohua1, WEI Bin1, ZHANG Pengpeng2, ZHAO Lianheng2

(1. Shenzhen Transportation Design & Research Institute, Shenzhen 518003, China; 2.School of Civil Engineering, Central South University, Changsha 410075, China)

In view of the difficulty in calculating the parameters of the hyperbolic model of lateral resistance, a simplified trilinear model of lateral resistance is proposed, considering the existence of initial and ultimate shear stress and softening characteristics of lateral resistance of pile side soil. Based on the nonlinear relationship between the displacement of the pile end and the bearing capacity of the pile end, the hyperbolic model is used to simulate the load transfer shape of the pile end. Based on the above-mentioned load transfer models at the pile side and pile end, a simplified recursive analysis method is proposed to obtain the load-settlement relationship of a single pile. Engineering case analysis and numerical simulation analysis show that the model and calculation method proposed in this paper have good accuracy when applied to single pile settlement calculation, and the model parameters are easy to obtain and simple to calculate, which can provide reference for design and construction.

settlement of single pile; initial shear stress; trilinear model; multi-layered soils; numerical simulation

TU473

A

1672 ? 7029(2020)04 ? 0875 ? 07

10.19713/j.cnki.43?1423/u.T20191018

2019?07?19

湖南省交通運輸廳科技項目(201828)

趙煉恒(1980?)，男，湖南益陽人，教授，博士，從事道路與鐵道工程、巖土極限狀態分析理論與應用等研究；E?mail：zlh8076@163.com

(編輯 涂鵬)