承插型盤扣式鋼管支架盤扣節(jié)點抗扭剛度影響因素

陳桂香, 郭澤群, 胡德平, 徐 晨

(1.河南工業(yè)大學土木建筑學院， 鄭州 450001；2.中鐵十六局集團有限公司，北京 100018)

承插型盤扣式鋼管支架以其整體性好、承載力高、拆裝便捷、施工成本低等優(yōu)點，在各類建設工程施工中得到應用，成為模板支架的主流架體之一[1]。承插型盤扣式鋼管支架作為一種薄壁鋼管結構，穩(wěn)定承載力是影響其結構安全的主要因素[2]。由于連接構造原因，盤扣節(jié)點半剛性特性顯著，其抗扭剛度對架體穩(wěn)定承載力影響較大[3]。

為便于實際工程應用，《建筑施工臨時支撐結構技術規(guī)范》(JGJ300—2013)[4]和《建筑施工承插型盤扣式鋼管支架安全技術規(guī)程》(JGJ231—2010)[5]對承插型盤扣式鋼管支架盤扣節(jié)點半剛性的規(guī)定均采用線性定值，抗扭剛度分別為40 kN·m/rad和86 kN·m/rad。針對承插型盤扣式鋼管支架盤扣節(jié)點半剛性特性的相關研究普遍也采用線性定值，得出了35～90 kN·m/rad不等的盤扣節(jié)點抗扭剛度值[6-11]。隨著節(jié)點半剛性的深入研究，相關節(jié)點抗扭試驗研究和實體有限元模型數(shù)值模擬結果[8,12-13]表明：盤扣節(jié)點剛度隨著節(jié)點扭矩的增加而逐漸減小，非線性明顯。研究節(jié)點抗扭剛度的非線性特性，對架體穩(wěn)定承載力精確數(shù)值分析和盤扣節(jié)點受力性能改進具有一定的工程應用意義。

在盤扣節(jié)點扭試驗分析的基礎上，應用數(shù)理統(tǒng)計方法，得到了盤扣節(jié)點抗扭剛度的二參數(shù)對數(shù)非線性數(shù)學模型。結合有限元分析結果，提出了便于架體結構數(shù)值分析應用的3階段節(jié)點抗扭剛度取值，并通過架體壓載試驗驗證了其應用于架體穩(wěn)定承載力計算的合理性。結合試驗現(xiàn)象，應用有限元數(shù)值分析手段，分析研究了各影響因素對盤扣節(jié)點抗扭剛度的作用機理及影響，可為盤扣節(jié)點構造的改良提供數(shù)值分析和試驗數(shù)據(jù)支持。

1 盤扣節(jié)點抗扭試驗

1.1 試驗方案設計

從施工現(xiàn)場隨機抽取6組盤扣節(jié)點構件，每組盤扣節(jié)點構件包括一根立桿和一根水平桿。在試驗室對6組盤扣節(jié)點構件進行抗扭試驗，構件規(guī)格及材質如表1所示。

表1 構件規(guī)格及材質Table 1 The components specification and material

注：立桿、水平桿規(guī)格為外直徑(mm)×壁厚(mm)；連接盤規(guī)格為外直徑(mm)×厚度(mm)；插銷規(guī)格為厚度(mm)。

圖1所示為盤扣節(jié)點抗扭試驗。立桿長400 mm，上下兩端與鋼板焊接，然后在液壓臺上固定，兩端邊界條件為固接。水平桿長1 000 mm，在距離立桿軸心線1 000 mm處，采用砝碼對水平桿施加豎向集中力。加載形式采用分級加載，每級加載100 N，上一級加載完成后，等位移計讀數(shù)穩(wěn)定后，進行下一級加載，直至構件破壞或測點位移過大超出位移計量程時停止試驗。

1.2 試驗計算模型

引入抗扭彈簧模型[14]模擬盤扣節(jié)點的抗扭剛度，任意受力狀態(tài)下盤扣節(jié)點抗扭剛度為

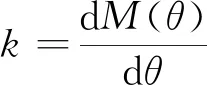
(1)

式(1)中：dθ為盤扣節(jié)點彈簧轉角增量；dM(θ)為盤扣節(jié)點扭矩增量；k為盤扣節(jié)點抗扭剛度。

盤扣節(jié)點抗扭剛度是扭矩關于轉角的導函數(shù)，通過盤扣節(jié)點扭矩和彈簧轉角的關系曲線，可定量分析盤扣節(jié)點的抗扭剛度，定性研究抗扭剛度的影響因素。盤扣節(jié)點抗扭試驗的計算模型如圖2所示。

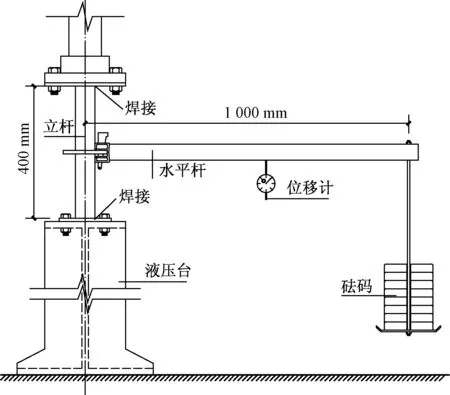
圖1 盤扣節(jié)點抗扭試驗Fig.1 Test on the torsional stiffness of the disk-pin joint node

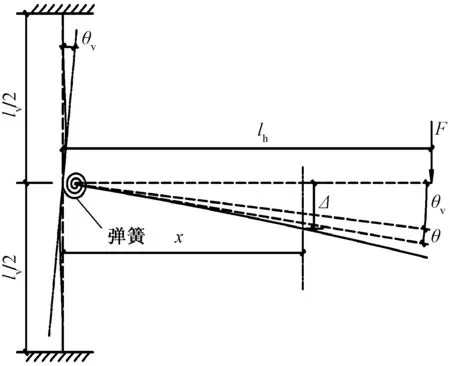
圖2 試驗計算模型Fig.2 Model of computation for test

采用小變形假設，忽略構件變形對構件尺寸的影響。水平桿在豎向集中力荷載作用下，盤扣節(jié)點處扭矩為

M=Flh

(2)

式(2)中：lh為水平桿豎向集中力作用點至立桿軸心線的距離；F為水平桿豎向集中力；M為盤扣節(jié)點扭矩。

扭矩作用下，盤扣節(jié)點處立桿轉角和盤扣節(jié)點彈簧轉角分別為

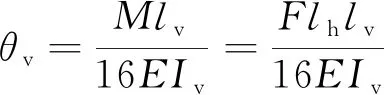
(3)

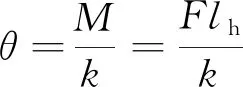
(4)

式中：Iv為立桿截面慣性矩；E為鋼材彈性模量；lv為立桿長度；θ為盤扣節(jié)點彈簧轉角；θv為盤扣節(jié)點處立桿轉角。

盤扣節(jié)點彈簧轉角、盤扣節(jié)點扭矩和測點豎向位移的關系為

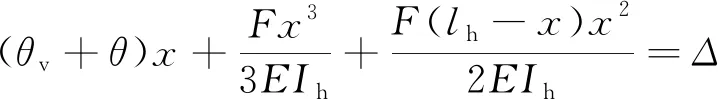
(5)

式(5)中：Δ為水平桿測點位移；Ih為水平桿截面慣性矩；x為水平桿測點距立桿軸心線的距離。

由式(3)～式(5)推導得盤扣節(jié)點扭矩與轉角的關系為

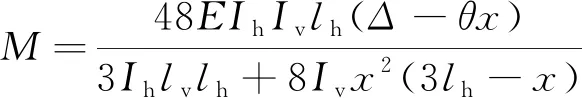
(6)

1.3 試驗數(shù)據(jù)處理

6組試驗實測力-位移數(shù)據(jù)，經(jīng)式(6)處理后，各組盤扣節(jié)點構件M-θ關系曲線如圖3所示。

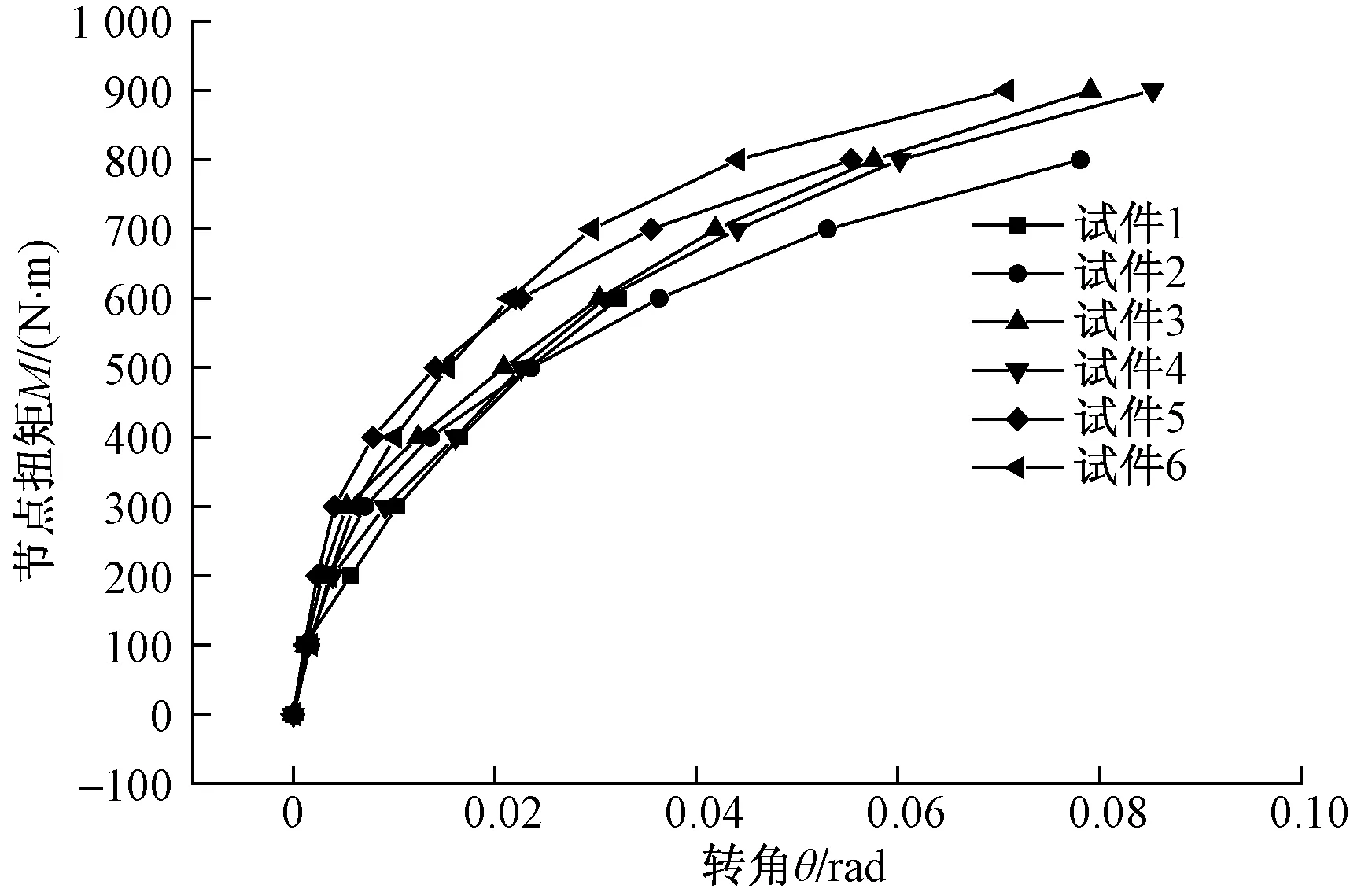
圖3 M-θ關系曲線Fig.3 The relationship curve of M-θ

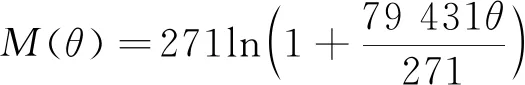
(7)

盤扣節(jié)點初始抗扭剛度為79.431 kN·m/rad。

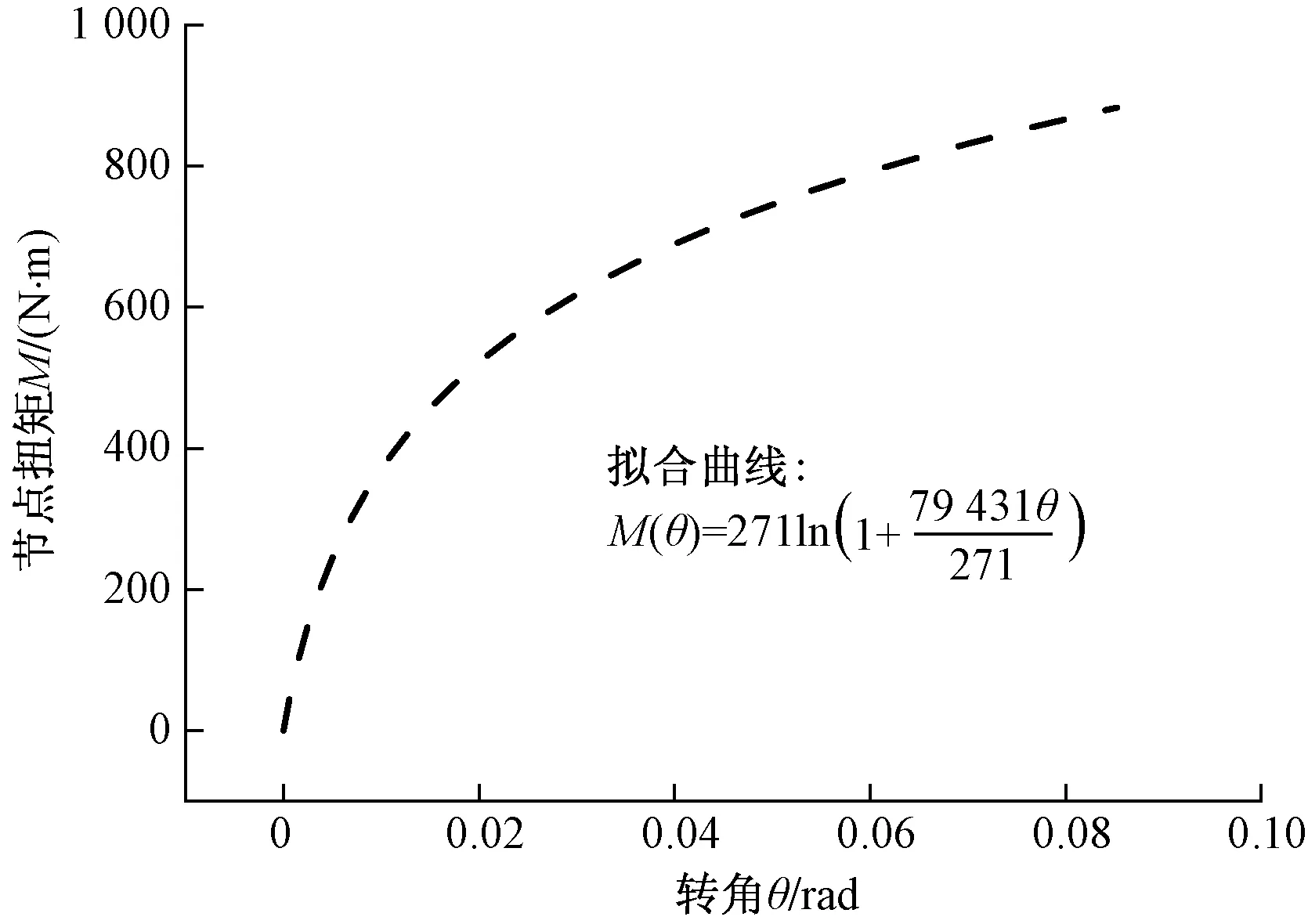
圖4 M-θ擬合曲線Fig.4 The fitting relationship curve of M-θ

1.4 試驗分析

試驗過后，6組試件中插銷與連接盤接觸處均出現(xiàn)了較大塑性變形，如圖5所示；6組試件中與水平桿扣接頭下翼緣接觸的立桿在接觸面邊緣部位均有明顯的塑性壓痕，如圖6所示。由此可知，插銷與連接盤接觸處和水平桿扣接頭與立桿接觸處的受力變形性能決定盤扣節(jié)點抗扭剛度。而影響插銷與連接盤接觸處和水平桿扣接頭與立桿接觸處的受力變形性能的因素主要包括材料彈性模量、材料應變硬化模量、插銷與連接盤接觸面積、水平桿扣接頭與立桿接觸面積。

圖5 連接盤與插銷破壞Fig.5 The destruction between disk plate and wedge

圖6 立桿破壞Fig.6 The destruction of standing tube

2 盤扣節(jié)點抗扭有限元數(shù)值分析

2.1 有限元分析模型創(chuàng)建

采用有限元數(shù)值分析軟件ANSYS，按盤扣節(jié)點實際尺寸創(chuàng)建盤扣節(jié)點三維有限元模型，對盤扣節(jié)點抗扭進行數(shù)值分析，邊界條件設置與試驗相同，盤扣節(jié)點三維有限元分析模型如圖7所示。

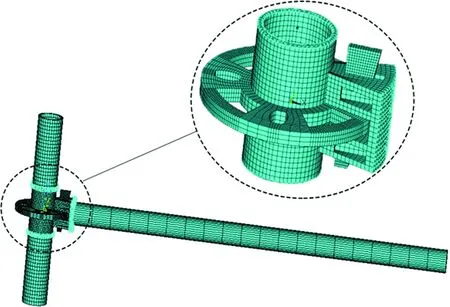
圖7 有限元分析模型Fig.7 The finite element analysis model

模型中，盤扣節(jié)點處實體模型采用SOLID185單元；水平桿和立桿采用BEAM188單元；水平桿、立桿與盤扣節(jié)點采用多點約束法(multipoint constraints,MPC)進行接觸連接；盤扣節(jié)點處各構件的之間的接觸行為采用接觸單元CONTA173和目標單元TARGE170進行模擬，接觸面行為設置為標準單向接觸，接觸摩擦系數(shù)取0.15。

Q345材質構件屈服強度取345 N/mm2，Q235材質構件屈服強度取235 N/mm2。構件材料模型采用雙線性等向強化模型(bilinear isotropic reinforcement model,BISO)，材料模型公式[16]為

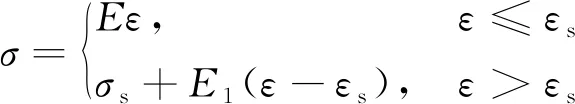
(8)

式(8)中：σ為材料應力；ε為材料應變；E為材料彈性模量，取2.06×105N/mm2；εs為材料屈服點處的材料應變；E1為材料應變硬化模量。

質量合格的鋼材彈性模量幾乎沒有變化，而應變硬化模量的變化范圍要比彈性模量大很多，平均值大約為彈性模量的1/50[17]。依據(jù)盤扣節(jié)點構造，對于給定規(guī)格的盤扣節(jié)點，水平桿扣接頭與立桿的接觸面積變化微小，但插銷與連接盤的接觸面積由于制造、安裝、長時間使用等因素差異性較大。

根據(jù)材料應變硬化模量不同、插銷與連接盤接觸面斜率差比不同，建立5個盤扣節(jié)點三維有限元模型進行數(shù)值分析，如表2所示。插銷與連接盤接觸面斜率差比為

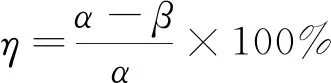
(9)

式(9)中：α為插銷接觸面與垂直面的夾角斜率；β為連接盤接觸面與垂直面的夾角斜率；η為插銷與連接盤接觸面斜率差比，當η=0%時，插銷與連接盤接觸面積最大，當η=100%時，插銷與連接盤接觸面積最小。

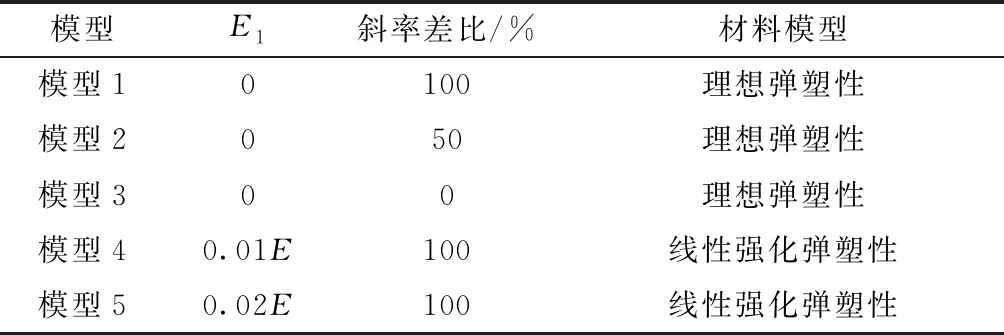
表2 有限元分析模型分類Table 2 The category of finite element analysis model

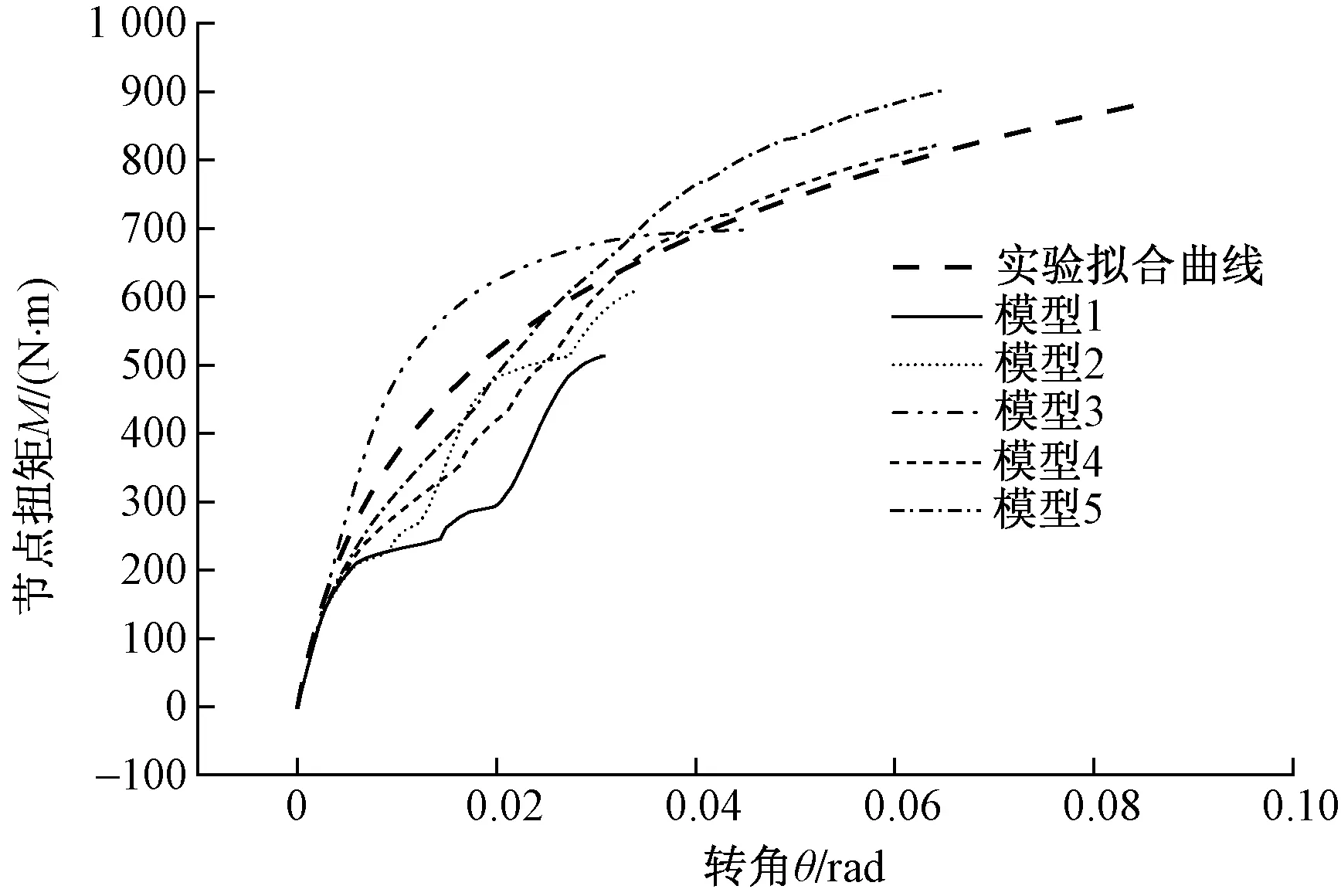
圖8 有限元分析模型曲線Fig.8 The curve of finite element analysis model

2.2 有限元數(shù)值分析結果分析

盤扣節(jié)點M-θ關系曲線的有限元數(shù)值分析結果如圖8所示。依據(jù)模型1～5的曲線走勢，將M-θ關系曲線分為3個階段。第1階段：構件基本處于彈性狀態(tài)，曲線近似直線上揚；第2階段：盤扣節(jié)點構件開始進入塑性狀態(tài)后，曲線斜率先變小后增大，形成一個下凹段；第3階段：盤扣節(jié)點構件塑形變形發(fā)展到一定程度后，扭矩增加緩慢，而轉角位移迅速增加，直至達到盤扣節(jié)點抗扭承載力。

在扭矩作用下，盤扣節(jié)點處于復雜的非線性受力狀態(tài)，包含材料非線性、幾何非線性和接觸非線性。這些非線性因素直接或間接地影響盤扣節(jié)點M-θ關系曲線走向，決定盤扣節(jié)點抗扭剛度。以模型1為例，闡述各影響因素對盤扣節(jié)點抗扭剛度的作用機理。

第1階段：模型1在盤扣節(jié)點扭矩小于150 N·m的時候，除插銷與盤扣節(jié)點連接盤接觸處存在局部小范圍的塑性變形外，盤扣節(jié)點各構件基本均處于彈性范圍內，最大塑性應變?yōu)?.3%，如圖9所示，M-θ關系曲線近似直線增長。

圖9 第1階段塑性變形Fig.9 The plastic deformation of the first stage

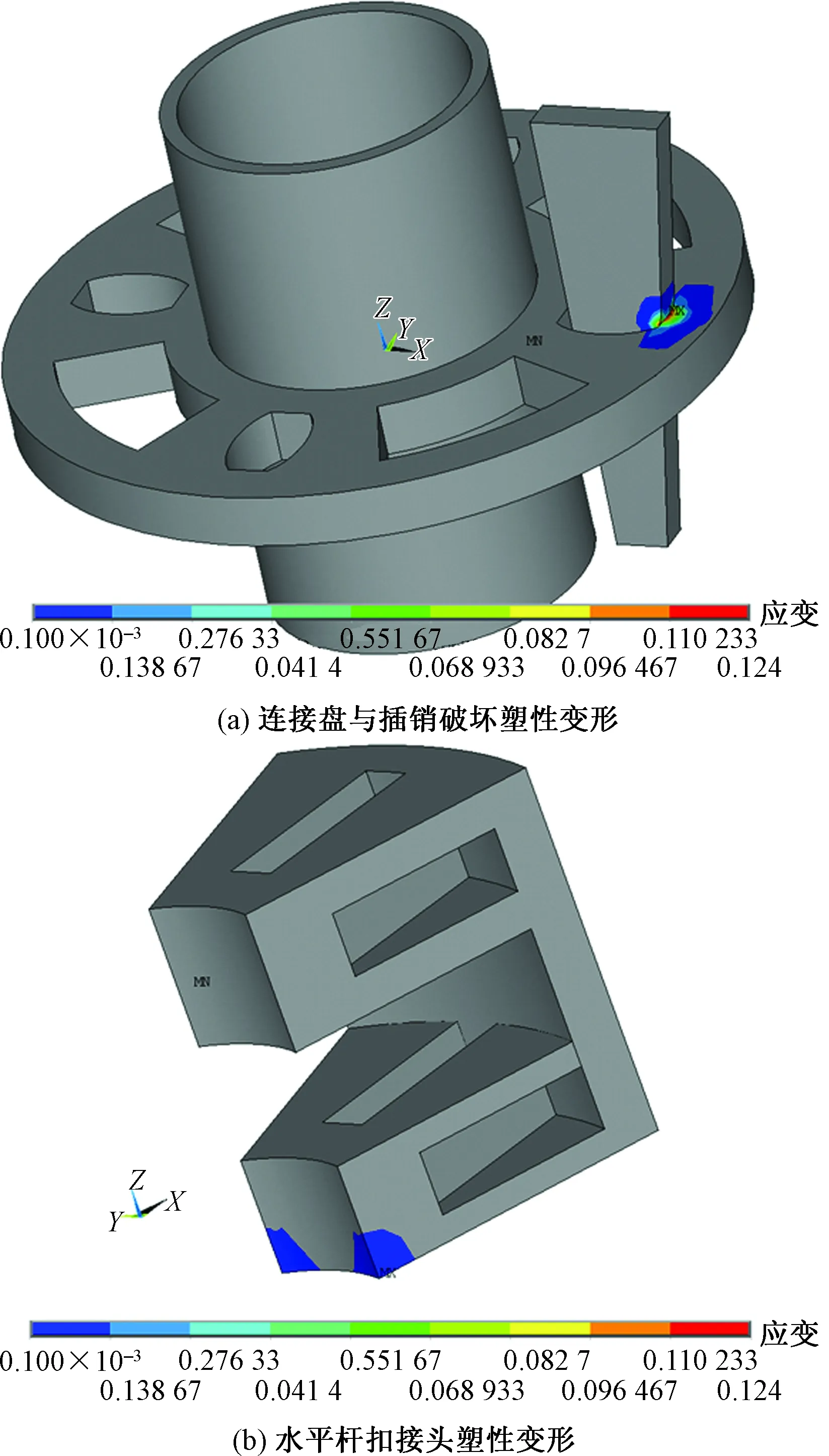
圖10 第2階段塑性變形Fig.10 The plastic deformation of the second stage

第2階段：模型1在盤扣節(jié)點扭矩150～250 N·m范圍內時，插銷與連接盤接觸處，由于接觸面積小，應力集中效應明顯，該處單元最大應變迅速從0.003增長到0.123，如圖10(a)所示，造成此范圍內M-θ關系曲線近似水平變化。扭矩為250～300 N·m范圍內時，隨著接觸點處塑性的發(fā)展，接觸面積相應增加，造成M-θ關系曲線短暫上揚，隨后水平桿扣接頭下緣角點出現(xiàn)較大塑性變形，如圖10(b)所示，M-θ關系曲線又趨于水平，扭矩在300 N·m以后，盤扣節(jié)點各構件的塑性區(qū)域不斷擴張，接觸面積進一步增加，使M-θ關系曲線斜率有所上揚。

第3階段：模型1在盤扣節(jié)點扭矩到達約500 N·m時，插銷塑性區(qū)域貫穿整個截面，如圖11所示，扭矩增加緩慢，而轉角位移迅速增加，盤扣節(jié)點變成可變體系，達到極限抗扭承載力。

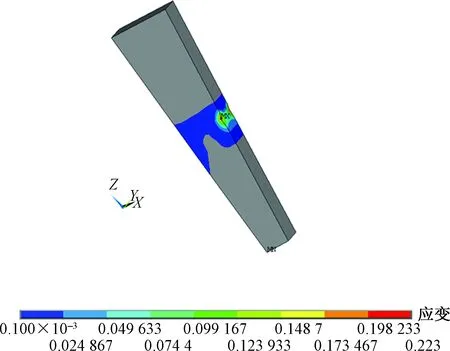
圖11 第3階段塑性變形Fig.11 The plastic deformation of the third stage

對比分析模型1～模型5的M-θ關系曲線，可得出以下結論。

(1)對比模型1～模型3，在插銷與連接盤接觸面積不同的情況下，第1階段盤扣節(jié)點抗扭剛度增加了7.9%，第2階段盤扣節(jié)點的受力變形性能得到明顯改善，第3階段曲線斜率近似一致，無明顯差別，插銷與連接盤接觸面積對盤扣節(jié)點抗扭剛度的影響可以忽略，但極限抗扭承載力得到提高。

(2)對比模型1、模型4、模型5，在材料應變硬化模量不同的情況下，第1階段盤扣節(jié)點抗扭剛度沒有變化；第2階段3條曲線逐漸趨于平滑，盤扣節(jié)點抗扭剛度得到較大提高。第3階段條曲線斜率基本一致，材料應變硬化模量對盤扣節(jié)點抗扭剛度的影響可以忽略。

由上述分析知：盤扣節(jié)點扭矩在0～150 N·m范圍內時，鋼材彈性模量得以保證的情況下，抗扭剛度變化范圍不超過7.9%。采用與試驗相同的二參數(shù)非線性模型擬合模型1的M-θ關系曲線，擬合函數(shù)為

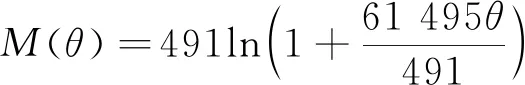
(10)

盤扣節(jié)點扭矩在大于150 N·m以后，5個模型的M-θ關系曲線雖然走向趨勢相同，但在變化程度上已發(fā)生較大差異，這是插銷與連接盤接觸面積和材料應變硬化模量共同作用的結果。由于插銷與連接盤接觸面積和鋼材應變硬化模量變化范圍較大，后兩個階段盤扣節(jié)點抗扭剛度應視具體構件規(guī)格，依據(jù)試驗數(shù)據(jù)確定。

3 抗扭剛度結果對比分析

3.1 盤扣節(jié)點抗扭剛度的影響因素

根據(jù)盤扣節(jié)點抗扭試驗和有限元數(shù)值分析結果，承插型盤扣式鋼管模板支架盤扣節(jié)點抗扭剛度影響因素分析如表3所示。

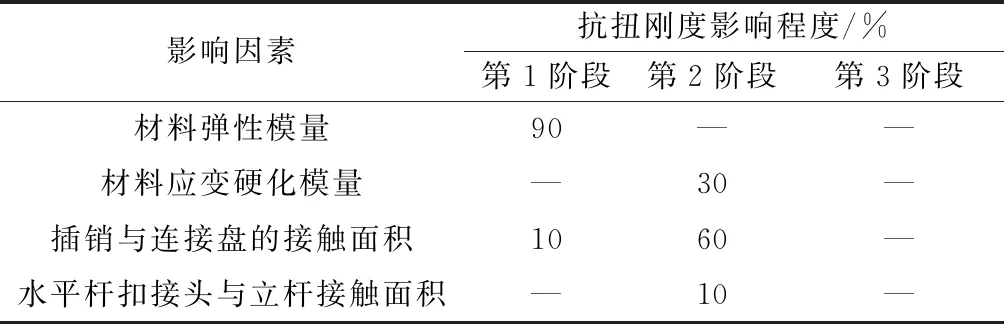
表3 盤扣節(jié)點抗扭剛度影響因素Table 3 The factors of torsional stiffness of disk-pin joint node

3.2 盤扣節(jié)點抗扭剛度值的確定

盤扣節(jié)點扭矩在0～150 N·m時，盤扣節(jié)點抗扭剛度的離散性較小，變化范圍約8%。承插型盤扣式鋼管支架結構設計中，盤扣節(jié)點構造及尺寸與表1相同，且盤扣節(jié)點扭矩不超過150 N·m時，盤扣節(jié)點抗扭剛度值建議取50～60 kN·m/rad。試驗曲線與模型1曲線第1階段初始抗扭剛度值和平均抗扭剛度值如表4所示。

表4 盤扣節(jié)點抗扭剛度Table 4 The torsional stiffness of disk-pin joint node

盤扣節(jié)點扭矩大于150～500 N·m后，插銷與連接盤接觸面積和材料應變硬化模量差異性較大，導致數(shù)值模擬的盤扣節(jié)點抗扭剛度離散性很大，可根據(jù)試驗擬合曲線函數(shù)進行選取，建議取20～25 kN·m/rad。

盤扣節(jié)點扭矩大于500 N·m后，盤扣節(jié)點構件塑形變形嚴重，不適宜繼續(xù)承受扭矩荷載，盤扣節(jié)點抗扭剛度建議取值為0～5 kN·m/rad。

4 抗扭剛度建議值驗證

采用長柱壓剪試驗機，通過三級分配鋼梁對承插型盤扣式支架鋼管支架進行壓載試驗。架體構件規(guī)格、材質同節(jié)點抗扭試驗，架體尺寸如圖12所示。

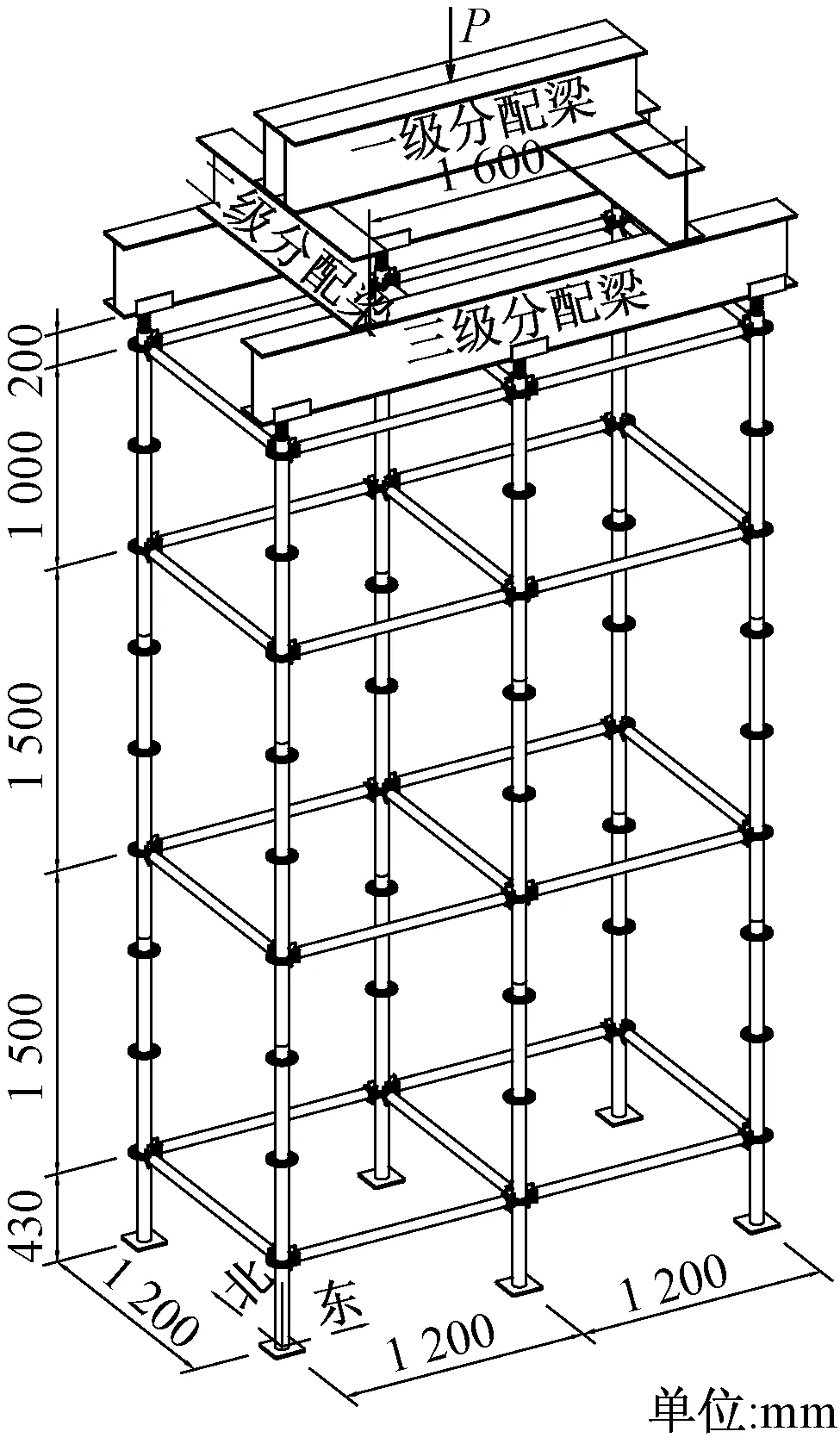
圖12 試驗架體Fig.12 Test frame

試驗架體荷載-側移曲線如圖13所示，當荷載達到282.44 kN時試驗架體失穩(wěn)屈曲。

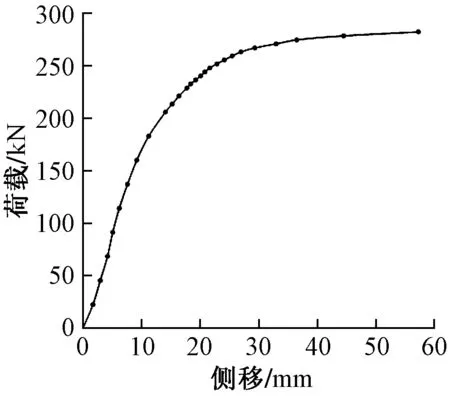
圖13 試驗荷載-側移曲線Fig.13 Test load-lateral displacement curve

采用有限元軟件ANSYYS創(chuàng)建2個試驗架體有限元模型，如表5所示。立桿和水平桿采用BEAM188梁單元，按理想彈塑性處理，材料模型采用雙線性等向強化模型BISO，應變硬化模量取0，材料屈服準則為Mises屈服準則。立桿屈曲強度取345 N/mm2，水平桿屈服強度取235 N/mm2。采用COMBIN39非線性彈簧單元模擬盤扣式節(jié)點處立桿和水平桿的半剛性連接。架體垂直度偏差取試驗架體實測值10 mm，立桿初始彎曲取規(guī)范[5]限值1.5 mm。

依據(jù)試驗架體現(xiàn)實邊界條件，設置架體有限元模型立桿底部和頂部為鉸接，對有限元模型進行非線性屈曲分析，數(shù)值分析結果與試驗結果對比如表6所示。試驗架體穩(wěn)定承載力數(shù)值分析值與試驗值誤差為-1.34%～-6.9%，滿足工程精度要求，且偏于安全，表明盤扣節(jié)點抗扭剛度建議值適用于實際工程。

表5 試驗架體有限元模型分類Table 5 The category of the test frame FEA model

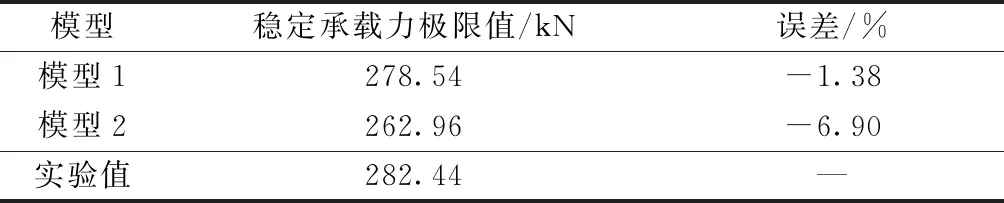
表6 穩(wěn)定承載力試驗值與數(shù)值分析值Table 6 The test value and the numerical analysis value of stability bearing capacity

5 結語

通過盤扣節(jié)點抗扭試驗和有限元數(shù)值分析，得出了承插型盤扣式鋼管支架盤扣節(jié)點抗扭剛度影響因素，其中插銷與連接盤的接觸面積和材料應變硬化模量影響較大。因此增大插銷與連接盤的接觸面積可以有效改善盤扣節(jié)點的抗扭性能。

盤扣節(jié)點抗扭剛度非線性特性明顯，分為3個階段進行選取比較合理，承插型盤扣式鋼管支架各階段的盤扣節(jié)點抗扭剛度建議值如下：盤扣節(jié)點扭矩小于150 N·m時，取50～60 kN·m/rad；盤扣節(jié)點扭矩在150～500 N·m時，取20～25 kN·m/rad；盤扣節(jié)點扭矩大于500 N·m時，取0～5 kN·m/rad。