基于文化螢火蟲算法-廣義回歸神經網絡的船舶交通流量預測
薛 晗,邵哲平,潘家財,張 鋒
(集美大學 航海學院, 福建 廈門 361021)
由于海上交通越來越繁忙,船舶交通流量快速増長,導致海上交通事故頻繁發生,造成巨大的經濟損失.船舶交通流量是海上交通工程學中一個重要的基本量,也是衡量海上交通基礎設施建設的一個重要指標,其預測結果能為相關主管部門制定科學航道管理規劃和做好船舶通航管理等工作提供基礎性依據.因此,保障船舶交通流量預測的準確性和合理性對于改善航道基礎設施建設與制定科學的航道管理策略等具有重要的意義.
船舶交通流量預測研究采用多種先進人工智能優化算法的預測模型,如人工神經網絡[1]、極限學習機[2]、模糊控制[3]、自回歸移動平均模型[4]、低秩稀疏分解[5]、支持向量機[6]、支持向量機回歸[7]、遺傳算法[8]及灰色理論[9]等人工智能算法.由于能處理復雜非線性問題,神經網絡取得了一定的成果.李俊等[10]采用遺傳算法改善神經網絡進行了船舶交通流量的預測.鈕浩東等[11]采用果蠅優化算法優化廣義回歸神經網絡(GRNN)進行了船舶交通流量預測.
然而,神經網絡本身存在一些不足,例如學習速度慢、容易陷入局部極值、學習及記憶不穩定性.文化算法(CA)是一種包含信仰空間與種群空間的雙層進化系統,種群空間的演化可以由信仰空間中保存的知識引導[12].螢火蟲算法(FA)是一種模擬自然界中成蟲發光的生物學特性優化算法[13-16].螢火蟲算法與其他算法結合,能改善螢火蟲算法的性能.Rizk-Allah等[17]將蟻群算法和螢火蟲算法結合起來求解無約束優化問題,該算法綜合了蟻群算法和螢火蟲算法的優點,螞蟻的演化是通過整合蟻群算法和螢火蟲算法來完成的,螢火蟲算法作為局部搜索來改進螞蟻發現的位置.Rahmani等[18]提出了一種混合進化螢火蟲遺傳算法,受螢火蟲社會行為和生物發光通信現象的啟發,將離散螢火蟲算法與標準遺傳算法相結合,提高了新算法的適應性,并應用于求解容量化設施選址問題.Kora等[19]提出了一種使用混合螢火蟲和粒子群優化技術,結合神經網絡分類器來檢測束分支塊的技術,新算法的光強吸引力是模擬最優解的主要控制力之一,光強吸引過程取決于搜索的隨機方向,局部搜索是通過粒子群優化算法(PSO)操作修改后的光強吸引步驟執行.本文設計一種新的文化螢火蟲算法,證明了算法的收斂性.利用新算法調整廣義回歸神經網絡(GRNN)的權值和閾值,提高神經網路的學習速度和性能,并將其應用于船舶交通流量的預測.
1 基于自動識別系統的航道交通流量統計
1.1 船舶交通流量模型
船舶交通流量的計算公式為
δ=ρvw
(1)
式中:ρ為船舶交通流密度;v為船舶交通流速度;w為船舶交通流寬度.
采用自動識別系統(AIS)進行船舶交通流量的測量統計,記錄某一段時間內船舶通過航道某一斷面的交通流量.如圖1所示,P1P2為觀測斷面,Q1Q2為船舶相鄰兩次AIS采集的位置軌跡連線.
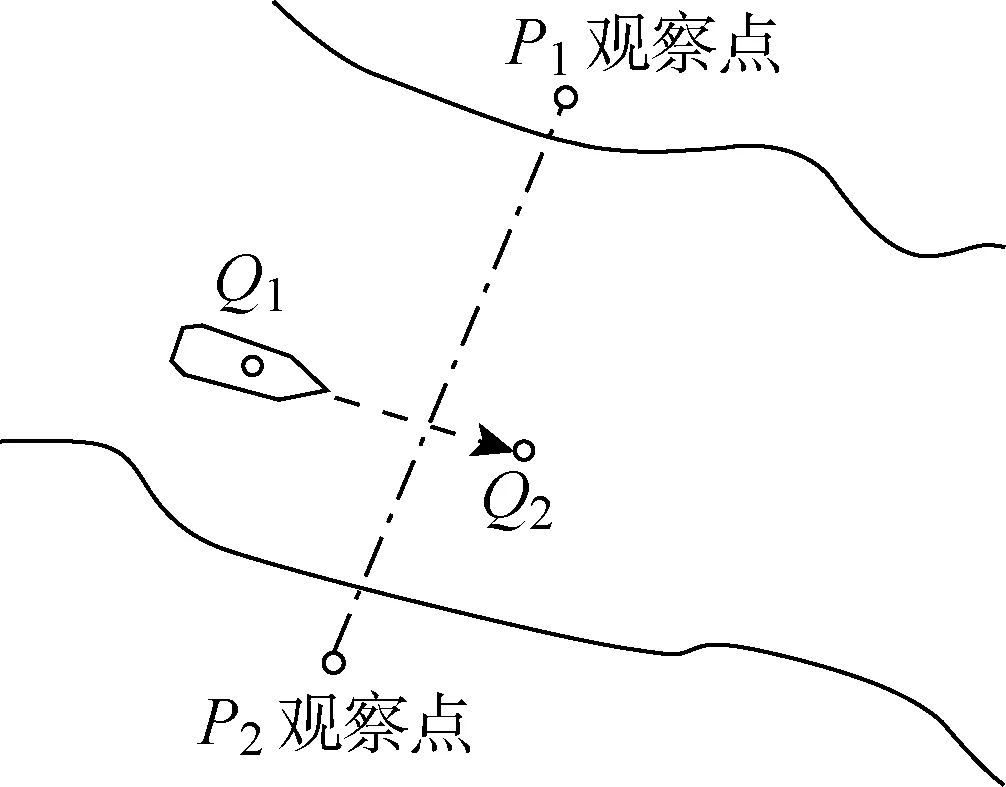
圖1 航行船舶航跡與航道觀察線Fig.1 Ship trajectory and channel observation line
兩條線段的位置關系有重合,相交及相離.按以下算法進行判斷圖1中船舶航跡Q1Q2與觀察線P1P2是否相交,如圖2所示.
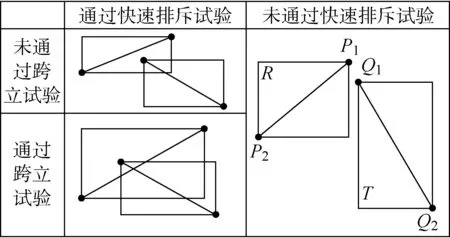
圖2 兩條線段相交關系判別Fig.2 Judge the intersection relationship of two line segments
(1) 快速排斥試驗:設以線段P1P2為對角線的矩形為R, 設以線段Q1Q2為對角線的矩形為T,如果R和T不相交,顯然兩線段不會相交.
(2) 跨立試驗:如果兩線段相交,則兩線段必然相互跨立對方.若P1P2跨立Q1Q2,則P1和P2兩點位于Q2和Q1的所在直線的兩側,用rxy表示x,y兩點間的矢量,則:
(rQ1P1×rQ1Q2)·(rQ1Q2×rQ1P2)>0
(2)
同理,判斷Q1Q2跨立P1P2的依據為
(rP1Q1×rP1P2)·(rP1P2×rP1Q2)>0
(3)
1.2 經緯度與直角坐標轉換
原始AIS數據只提供了船舶離散的地理坐標點位置,屬于經緯度類型的數據,而船舶的軌跡擬合基于船舶整體航行軌跡上進行分析處理.在軌跡擬合的過程中,需要將離散的軌跡點在擬合程序中有序重組,轉化為船舶航行軌跡線,在此過程中需要使用的數據是平面直角坐標系,所以在進行擬合之前需要將從AIS系統中獲取的經緯度數據轉換為墨卡托直角坐標系數據.
將經緯度數據轉換為墨卡托平面坐標系數據的方法如下[20].基準緯度處橢球的卯酉圈曲率半徑
(4)
式中:a為地球橢球長半徑;e為橢球體第一偏心率;φ0為墨卡托投影的基準緯度.基準緯度的緯圈半徑為
r0=N0cosφ0
(5)
等量緯度為
(6)
式中:φ為緯度.墨卡托直角坐標的橫坐標為
xn=r0λ
(7)
λ為經度.墨卡托直角坐標的縱坐標為
yn=r0q
(8)
2 廣義回歸神經網絡基礎

(9)
式中:k為訓練樣本數;Yi是y的第i個訓練樣本值;Di為X與Xi間歐氏距離;σ為平滑參數.模式層各單元傳遞函數為
(10)
求和層一個單元的傳遞函數為
(11)
其他單元傳遞函數為
(12)
式中:Yij式中為Yi的第j個元素.樣本預測值的第j個元素,即輸出層單元yj為
(13)
GRNN的結構如圖3所示.
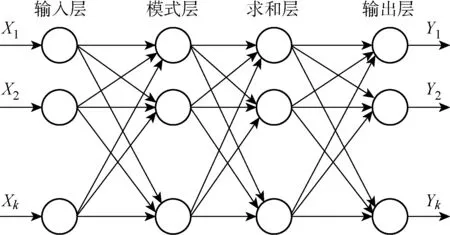
圖3 GRNN結構Fig.3 Structure of GRNN
3 文化螢火蟲算法
結合文化算法與螢火蟲算法的優點, 提出一種基于文化算法框架的螢火蟲優化算法,即CFA.
3.1 CFA的模型
螢火蟲個體i相對個體j的熒光亮度為
Ii=I0ie-γ rij
(14)
式中:I0i為個體i的最大熒光亮度,與其目標函數相關,目標函數越優則亮度越高;γ為光強吸收系數;rij為螢火蟲個體i和j之間的距離,
(15)
式中:d為問題的維數;xik為第i個螢火蟲的第k維分量.螢火蟲個體i和j之間的吸引力為
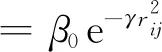
(16)
式中:β0為個體最大吸引力.若個體j的亮度高于個體i的亮度,即Ij>Ii,則個體j吸引個體i向自己方向移動,其位置x更新如下式:
(17)
式中:t為時間;α為步長;rand(0,1)為[0,1]之間均勻分布的隨機數.
信仰空間由在進化過程中獲取的經驗和知識組成,根據現有的種群經驗如最好個體以及新個體經驗進行更新.用當前最優個體xbest來更新信仰空間Belief的知識b,如下式:
(18)
信仰空間Belief通過下式規則來影響種群空間:
xik(t+1)=
(19)
式中:xij(t)為第t次迭代中第i個個體中第k維分量;ei為Belief中變量i可調整區間的長度;N(0,1)為服從標準正態分布的隨機數.
3.2 CFA流程
CFA的偽代碼如下所示:
(1) CFA程序;
(2) 開始;
(3)t∶= 0;
(4) 初始化算法參數,例如β0,γ,α;
(5) 初始化種群空間,例如螢火蟲位置;
(6) 計算每個螢火蟲的適應度,作為其最大亮度;
(7) 初始化信仰空間;
(8) 根據式(14)計算螢火蟲的相對亮度;
(9) 根據式(16)計算螢火蟲的吸引力;
(10) 根據式(4)更新螢火蟲的位置;
(11) 重新計算螢火蟲的亮度;
(12) 根據式(18)更新信仰空間;
(13) 根據式(19)影響種群空間;
(14)t∶=t+1;
(15) 當t (16) 輸出全局最優值和最優解; (17) 結束CFA. 先給出隨機優化算法收斂于全局最優的判據[22],再證明CFA的收斂性.設A為優化問題的可行解空間,f為目標函數,ξ為算法D在迭代中搜索過的最優解,第k次迭代結果生成的解為zk. 假設1若f(D(zk,ξ))≤f(zk),且ξ∈A,則f(D(zk,ξ))≤f(ξ). 假設2對于A的任意Borei子集B,若其勒貝格測度ν(B)>0,μk(B)為由測度μk獲得B的概率,則有: (20) 引理1假設目標函數f為可測函數,可行解空間A為Rn上的可測子集,R為實數集,Rε為全局最優解集,P(zk∈Rε)表示第k步算法生成的解zk屬于最優解Rε的概率,若假設1和2成立,則有: (21) 引理2有限齊次Markov鏈從任意非常返狀態出發依概率1要達到常返狀態. 定理1FA所表示的Markov鏈是有限時齊的. 證明螢火蟲個體位置更新的轉移概率P為 Pi j{xt+1=j|xt=i,xt-1=it-1,…,x0=i0}= P{xt+1=j|xt=i} 所以FA所表示的Markov鏈是有限時齊的. 定理2CFA中Belief的狀態的隨機變化屬于有限齊次Markov鏈. 證明CFA中Belief是用來記錄搜索過程中的進化知識,CFA對目標最優值的搜索是在離散的、有限的空間中進行的,因此用來記錄的Belief也是有限的.同時Belief每一次狀態轉移概率只和其當前狀態有關,而與t無關.因此,CFA的Belief的狀態的隨機變化屬于有限齊次Markov鏈. 定理3CFA依概率1全局收斂. 證明設信念空間Belief的全局知識的狀態空間為Ωg,局部狀態空間為Ωl,整個信念空間狀態空間為Π={(Ig,Is)},其中Ig表示全局知識集,Is表示螢火蟲群體空間的局部集. Π分為兩個子空間,即為常返狀態空間Π1和非常返狀態空間Π2,其中常返狀態空間可表示為 Π1={(Ig,Is)|Ig∈Ωg,Is∈Ωl} 則有Π2∩Π2=?,Π2∪Π2?Π. 若存在某知識狀態s∈Π1,則由全局知識的定義可知,將不再轉移到Π2,所以Π1為閉集.Π1中的狀態是相通的,所以Π1中狀態為常返狀態.若s∈Π2,由于Π2中的狀態為非常返狀態,進化過程中每一個體將在整個解空間范圍內運動,s由Π2轉向Π1的轉移概率大于0,故進化后的群體收斂于全局最優解的概率大于0.由引理2知,信念空間知識的進化由任意非常返狀態必然依概率1轉移到常返狀態,即依概率1收斂到全局最優解. CFA以神經網絡的輸出均方差為適應度函數,以神經網絡的輸入層和隱含層中的權值、隱含層和輸出層中的權值、隱含層的閾值及輸出層的閾值為編碼,對神經網絡進行優化,進化目標是得到最合適、最優的神經網絡結構.神經網絡用于預測前,需先進行訓練.預測流程如下: 步驟1初始化神經網絡模型; 步驟2輸入訓練樣本; 步驟3設置CFA參數和初始種群; 步驟4用CFA計算神經網絡的最優權值和閾值; 步驟5計算神經網絡隱藏層; 步驟6計算神經網絡輸出層; 步驟7計算神經網絡的輸出誤差; 步驟8若誤差不滿足學習要求,轉步驟 4,直至訓練結果達到要求為止; 步驟9用求得的最優權值與閥值初始化神經網絡; 步驟10輸入預測數據進行預測,輸出預測結果. 本文采用的AIS數據為舟山螺頭航道2016年1月的船舶交通流量數據.下列是預測過程使用的數據,并將原始數據轉換為墨卡托直角坐標系數據.水上移動通信業務標識碼(MMSI)為232971000的船在2016年1月28日的軌跡數據如表1所示. 我國學者提出考慮船舶尺寸大小和船舶總噸位的船舶換算系數,如表2所示,該系數能夠更準確地反映水域船舶交通狀況和繁忙程度. 表1 船舶AIS數據與轉換結果Tab.1 Ship AIS data and conversion results 表2 船舶大小和船舶總噸位的船舶換算系數Tab.2 Conversion coefficient of ship size and gross tonnage 舟山螺頭航道2016年1月1日至6日的船舶交通流量按每小時統計,如表3所示. 表3 舟山螺頭航道船舶交通流量Tab.3 Ship traffic flow in Zhoushan Luotou Channel 圖4 CFA優化的GRNN結構收斂曲線Fig.4 Convergence curve of GRNN structure optimized by CFA 用CFA優化GRNN的結構,進化收斂曲線如圖4所示,圖中n為進化代數,δ為適應度.CFA種群規模設置為30,最大進化迭代次數為30. 優化后的神經網絡結構參數如表4所示. 表4 優化后的神經網絡結構參數Tab.4 Optimized neural network structure parameters 本文采用前4 h的船舶交通流量數據,預測第5 h交通流量,如用2016年1月1日0∶00至4∶00的交通流量作為預測2016年1月1日4∶00至5∶00的船舶交通流量的訓練樣本數據,以此類推,實現對舟山螺頭航道船舶交通流量的預測.表5為所預測的2016年1月7日0∶00至5∶00的交通流量.圖5為船舶交通流量預測結果曲線. 表5 優化后的神經網絡預測結果Tab.5 Prediction results of optimized neural network 圖5 船舶交通流量預測結果曲線Fig.5 Prediction result curve of ship traffic flow 表6為不同算法預測2016年1月1日4:00至5:00的船舶交通流量的預測結果比較,算法分別為支持向量機(SVR),模糊控制(Fuzzy),不經過優化的原始GRNN,只用FA優化的GRNN(FA-GRNN)和用CFA優化的GRNN(CFA-GRNN). 結果表明,CFA優化神經網絡后,相比支持向量機, 模糊控制, GRNN和FA-GRNN都能提高神經網絡學習速度和預測準確度,具有泛化性能好、不易陷入局部最優等優勢.因此CFA優化神經網絡能夠更好地預測海域的船舶交通流量. 螺頭水道的船舶交通密度的變化受潮汐變化,晝夜變化的影響明顯,呈現出周期性的變化.舟山的潮汐情況如表7所示. 表7 舟山潮汐表Tab.7 Zhoushan tide 用高峰前10 h的船舶交通流量數預測高峰時段的船舶流量,如預測2016年1月10日 5∶00 至6∶00 的交通流量,2016年1月11日 6∶00 至 7∶00 的交通流量,2016年1月12日 7∶00 至 8∶00 的交通流量和2016年1月13日 8∶00 至 9∶00 的交通流量.預測結果如表8所示. 上表的結果進一步檢驗了模型和算法的有效性和正確性. 螺頭水道通航的大型船舶和小型船舶航行規律明顯不同,對交通環境的影響不同,交通組織優化的策略也不同.船長不小于200 m的船舶歸為大型船舶,船長小于120 m的船舶歸為小型船舶.流經舟山螺頭水道的不同類型船舶舉例如表9所示,具體信息包括MMSI、船長、國際海事組織(IMO)、呼號和船籍國. 表8 優化后的神經網絡預測結果Tab.8 Prediction results of optimized neural network 表9 舟山螺頭航道不同類型船舶 Tab.9 Different types of ships in Zhoushan Luotou Channel 類型MMSI船長/mIMO呼號船籍國大船5667960003699631955S6LT9新加坡4772744003669467299VRJS5香港56574700033793425169VBN2新加坡小船41359113059703936YYYY中國413508170899359234BMFA中國6360099481139065429ELQE5中國 對大型船舶和小型船舶分組進行預測.采用前10 h的船舶交通流量數據,預測接下來第11 h交通流量,如用2016年1月1日 0∶00 至 10∶00 的交通流量作為預測2016年1月1日 10∶00 至 11∶00 的船舶交通流量的訓練樣本數據,以此類推,來實現對舟山螺頭航道船舶交通流量的預測.表10為所預測的2016年1月7日 0∶00 至 9∶00 的大型船舶和小型船舶的交通流量結果. 表10 不同類型船舶的預測結果Tab.10 Prediction results of different types of ships 從上表可以看出,總體而言,漲潮時較多船舶進港,退流時較多船舶出港,通航密度大.大船的交通流量較穩定,交通流量隨時間變化相對不明顯;小船的交通流相對較為復雜,穿越航道的時間段也不是很固定,交通流量隨時間變化較大. (1) 設計了新的文化螢火蟲算法,證明了其收斂性,能有效改進GRNN的權值和閾值,泛化性能好,不易陷入局部最優,提高預測性能. (2) 應用CFA-GRNN對舟山螺頭航道船舶交通流預測,實驗結果和誤差分析證明了CFA優化廣義回歸神經網絡能夠更好地預測海域的船舶交通流量. (3) 用高峰前數小時的船舶交通流量數預測高峰時段的船舶流量,進一步檢驗模型和算法的有效性和正確性,并對大型船舶和小型船舶分組進行預測.3.3 CFA的收斂性分析
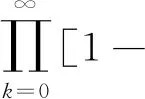
3.4 基于CFA的神經網絡預測船舶交通流量
4 實例與分析
4.1 實驗數據介紹
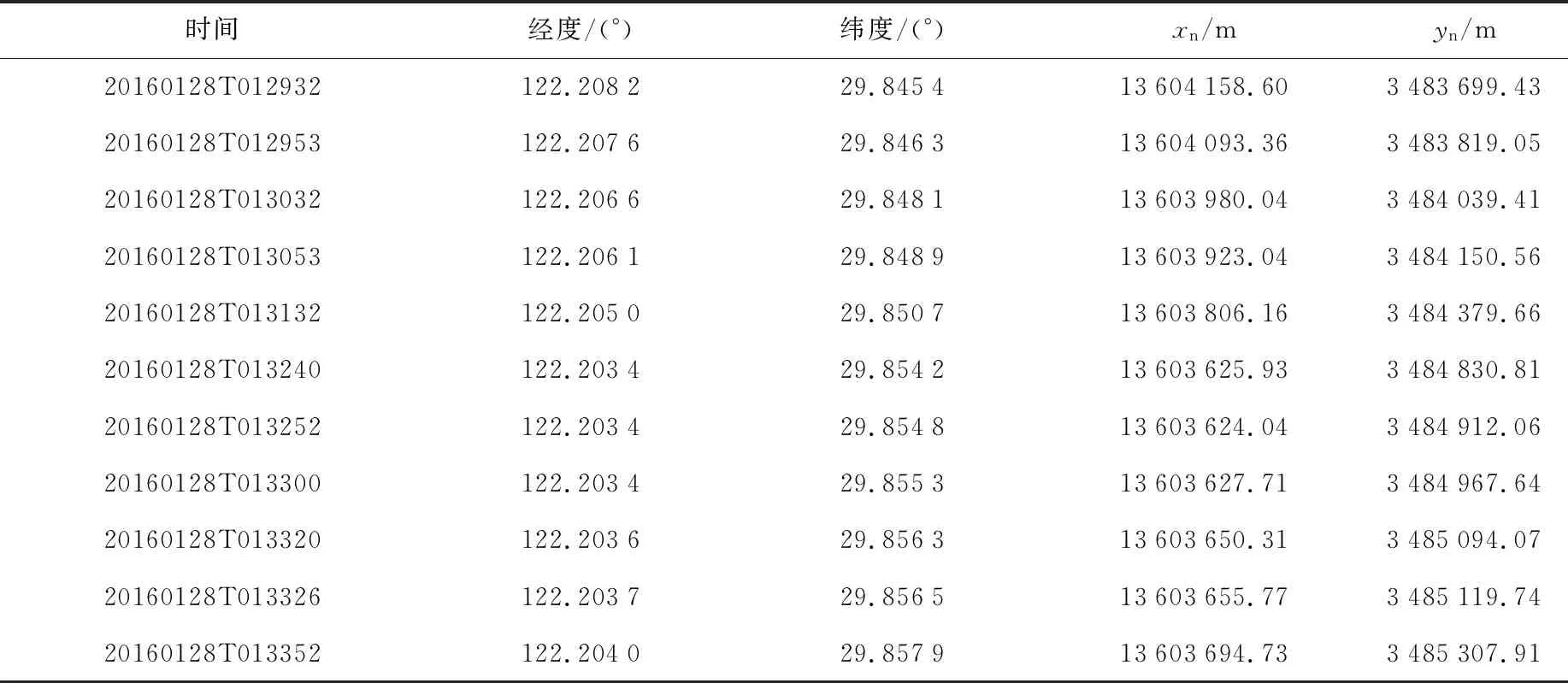

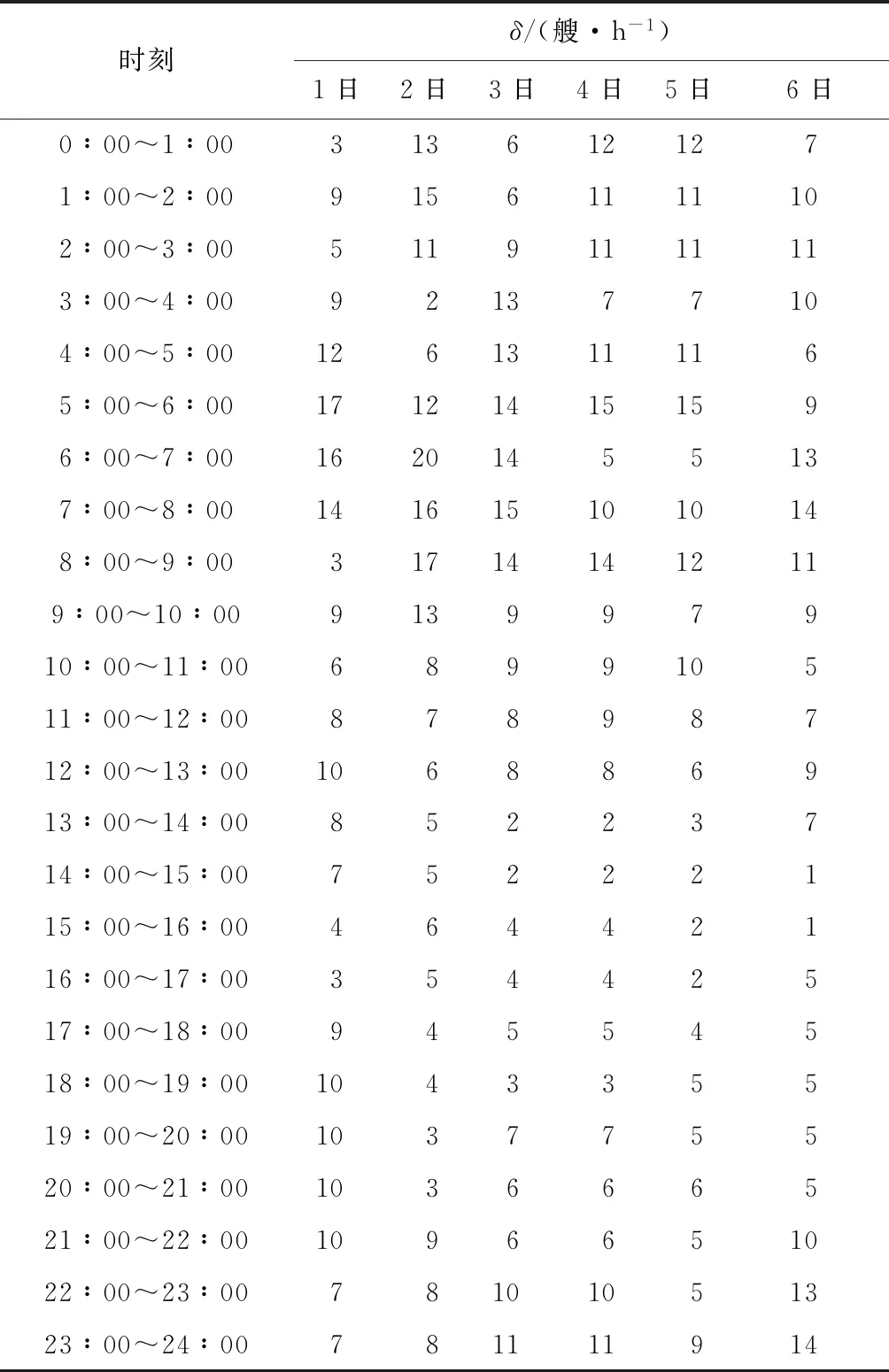
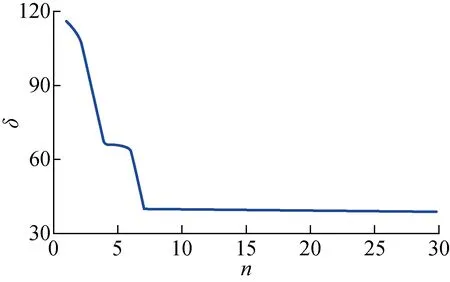
4.2 神經網絡結構優化

4.3 船舶交通流量預測
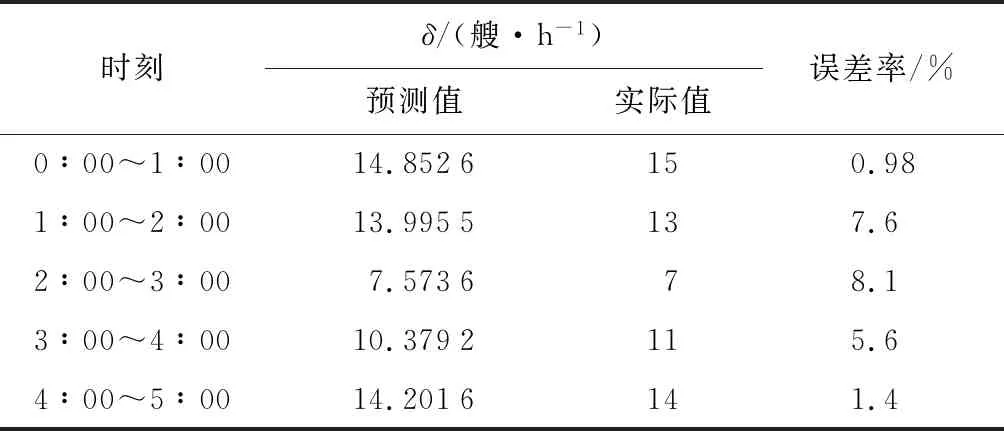
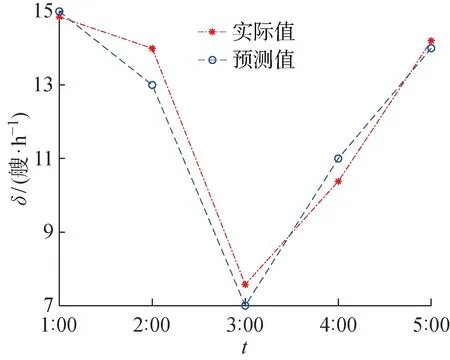
4.4 潮汐變化因素分析
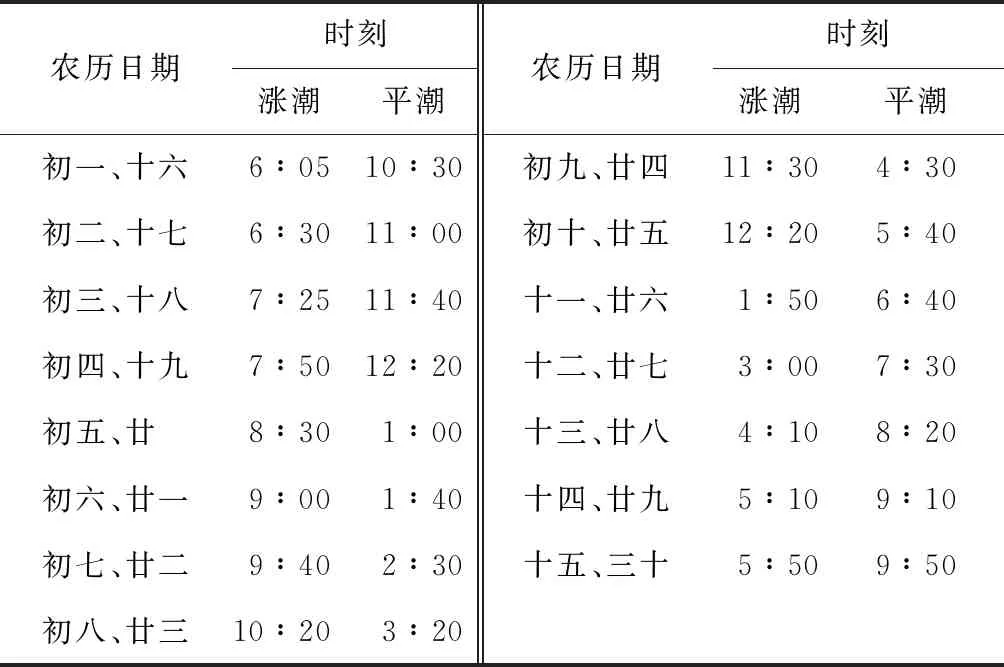
4.5 船舶類型因素分析
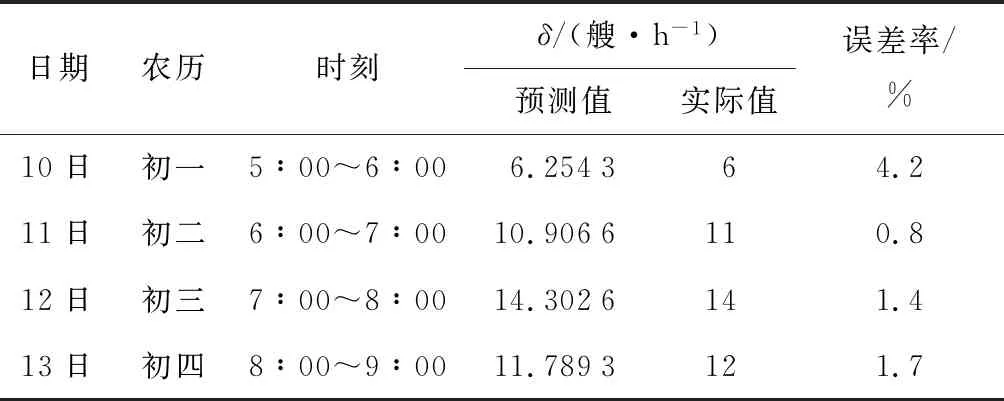
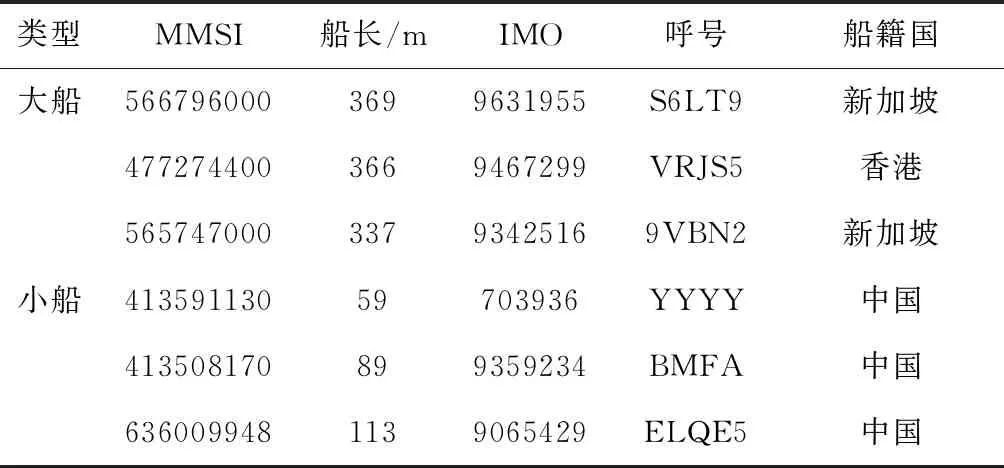
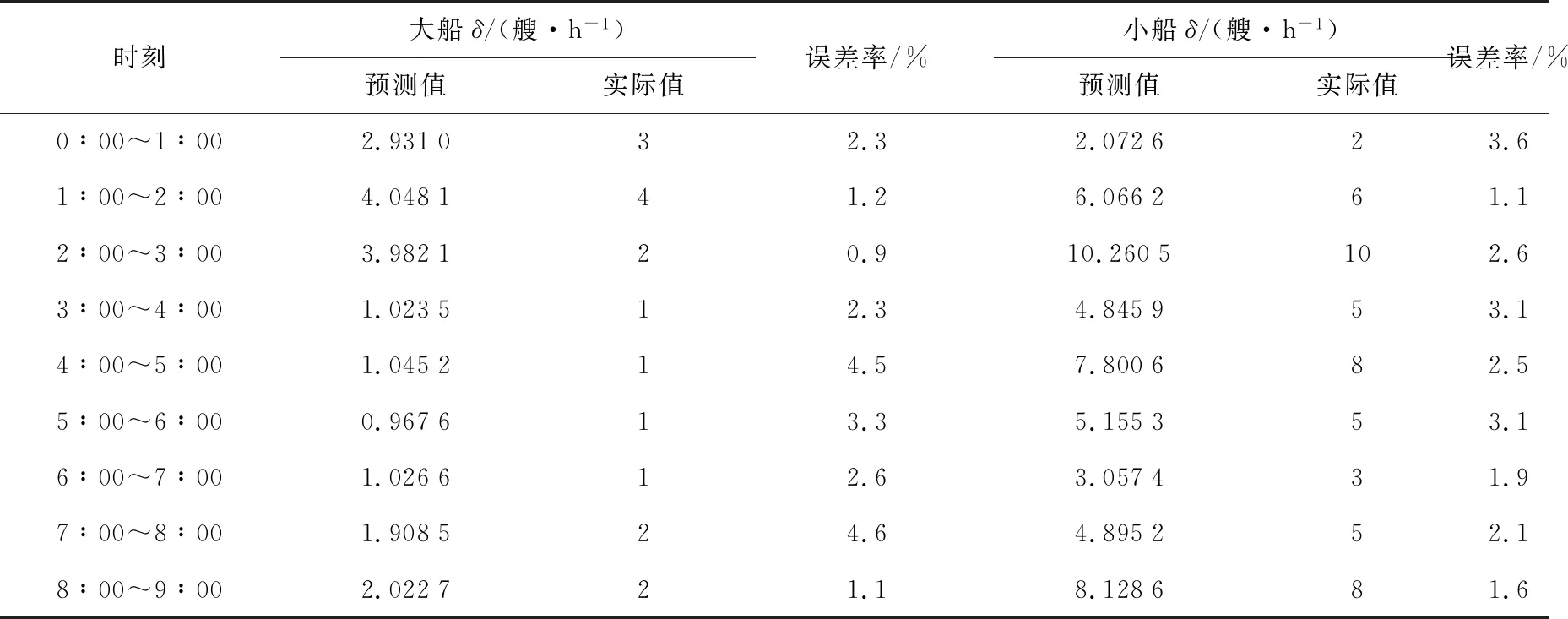
5 結論

