基于模糊迭代算法的曲面恒力跟蹤

張 鐵，肖 蒙，鄒焱飚，肖佳棟

(華南理工大學 機械與汽車工程學院， 廣州 510640)

機器人與環境接觸過程中，通過力控制能夠調節機器人與環境接觸狀態，從而達到理想的接觸效果，因此力控制廣泛運用于機器人打磨[1]、拋光[2]及曲面跟蹤等.利用機器人跟蹤未知曲面時，保持恒定的接觸力能夠得到精確的曲面輪廓.然而，在接觸過程中，由于機器人自身屬性[3](如機器人動力學特性，機器人剛度[4]以及未知環境是時變的(如曲面輪廓變化)，造成了機器人與曲面的接觸力不穩定，波動較大，從而導致采集的曲面輪廓不夠精確.

機器人恒力跟蹤的研究大致可以分為傳統控制(包括阻抗控制，力/位混合控制，自適應控制)和智能控制.傳統控制方法中，吳得祖[5]利用六維力傳感器對并聯機器人和曲面接觸點的剛度進行了測量，通過剛度控制對曲面進行恒力跟蹤.Winkler等[6]在力/位混合控制中加入額外的積分器來減少靜態控制誤差，同時通過改變機器人速度來達到跟蹤力恒定.智能控制中，Ye等[7]提出一種自適應模糊控制算法，在線對機器人的參數進行模糊補償以適應環境的變化，自適應模糊控制器具有良好的魯棒性.Jung等[8]在阻抗控制中加入了神經網絡補償，消除了不確定性的因素，包括環境中不確定性因素(如位置，剛度)以及機器人運動學中參數的變化造成的干擾.在三連桿機器人進行的仿真研究中，神經網絡補償的力控制器使得機器人能夠在未知環境中保持恒定的力，表現出良好的力跟蹤性能.Wang等[9]利用模糊神經網絡估計機器人在未知環境中所處的狀態，在不同狀態下通過調節不同的力控制參數來適應環境的變化，達到保持恒定力的狀態，最后通過兩自由度的連桿仿真驗證了算法的可行性.王磊等[10]通過模糊推理智能地預測阻抗控制模型中的參考軌跡，并根據力誤差變化調節參考比例因子，以適應未知環境剛度的變化，仿真結果證明了算法的有效性.

目前的研究中，傳統控制算法很難補償機器人跟蹤過程中的各種不確定性，如機器人運動學的不確定性[11]，機器人末端傳感器姿態的改變造成傳感器示數的變化，而智能控制算法設計比較復雜，大多停留在仿真階段.本文在力/位混合控制的基礎上針對力控部分提出一種模糊迭代的智能算法，在機器人內部傳遞函數未知和機器人末端傳感器姿態不改變的情況下，利用模糊算法補償軌跡的誤差，離線迭代更新機器人的軌跡，多次實驗后，使得接觸力在閾值范圍內波動，最終得到比較穩定的跟蹤力和較為精確軌跡.相比于傳統的比例積分(PD)控制和迭代算法，模糊迭代算法能夠得到更加穩定的跟蹤效果和軌跡.

1 曲面跟蹤運動受力分析

機器人恒力跟蹤實驗平臺如圖1所示，工作臺坐標系S，傳感器坐標系T和機器人基坐標系B的映射關系可以通過齊次變換矩陣來描述：

(1)

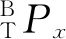
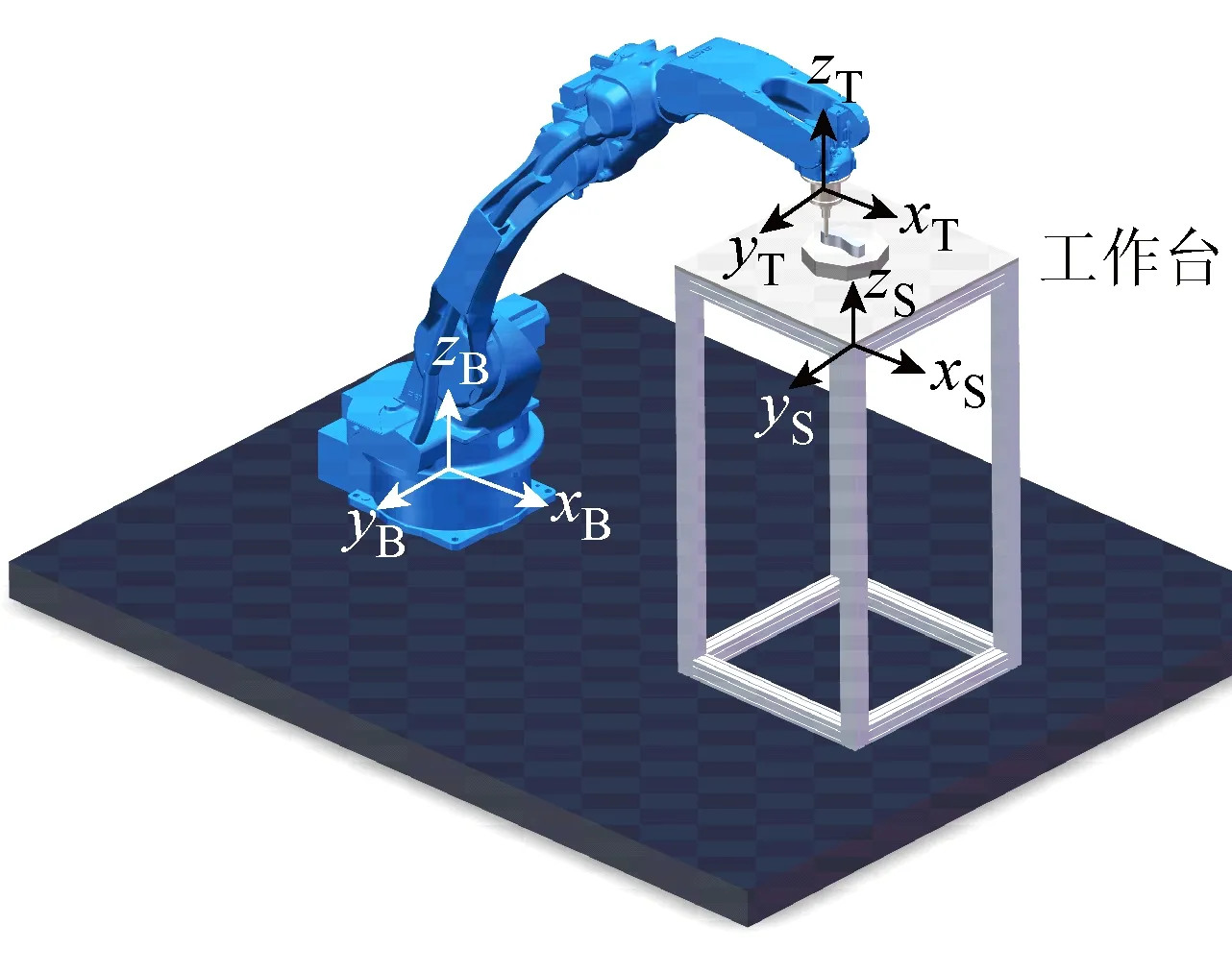
圖1 機器人恒力跟蹤實驗平臺Fig.1 Robot constant force tracking experimental platform

傳感器安裝在機器人末端，機器人通過安裝在傳感器上的探頭與環境接觸，如圖2所示，在跟蹤實驗中，機器人保持vs的速度沿著xV方向運動，機器人運動坐標系V和傳感器坐標系T的姿態始終相同.當探頭與曲面接觸時，探頭受到曲面的法向力Fn和切向力Fτ，恒定的Fn能夠反應出曲線的輪廓，為了得到Fn的大小，需要將曲面坐標系C中的力映射到已知的傳感器坐標系T中，曲面坐標系C中心與傳感器坐標系T中心重合，x軸方向與曲面的切向方向相同，y軸方向始終垂直于曲面輪廓，由圖3中受力分析可知:

(2)

圖2 機器人末端局部圖Fig.2 Partial view of the robot end-effector

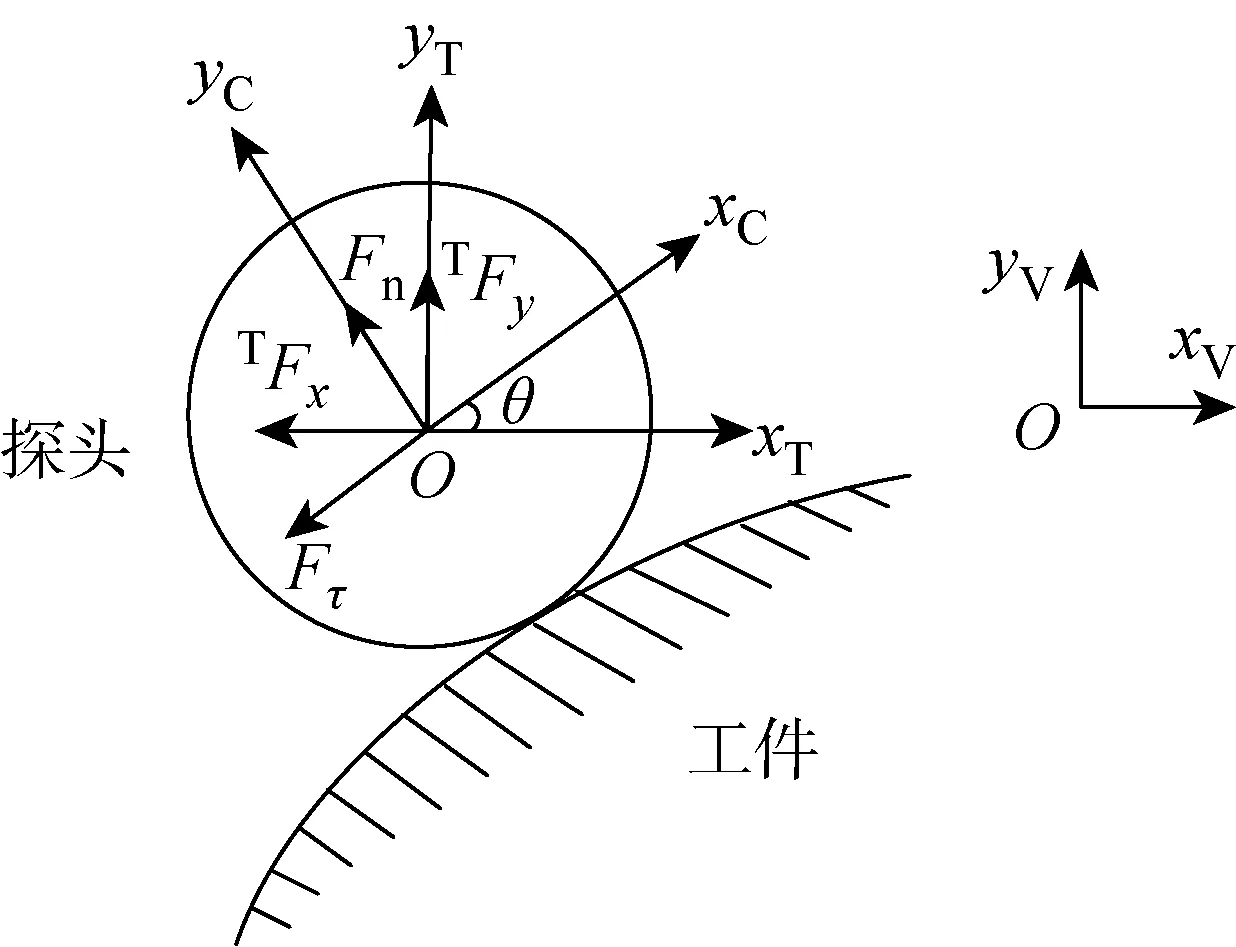
圖3 機器人末端受力分析圖Fig.3 Force analysis at the robot end-effector

式中：TFx和TFy分別為T坐標系下Fx和Fy；θ為xT與xC之間的夾角.將式(2)解耦可得:

(3)

TFx和TFy的大小可通過六維力傳感器測得.θ在T坐標系下等于曲面切線傾斜角，因此需要對θ進行估計.在傳感器T坐標系中，當機器人沿著xV方向和yV方向移動時，根據xV方向和yV方向上位移的差分可以得到每一小段的切線傾斜角為

(4)

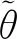
2 模糊迭代算法

迭代學習控制適合于具有重復運行特性的被控對象[12]，由于迭代算法在無需系統的傳遞函數[13]的情況下，根據誤差多次迭代就能達到所需要的狀態，所以大大降低了機器人控制算法設計的難度.

機器人跟蹤過程是離散的系統[14]，當機器人與環境剛性接觸時[15]，通過改變機器人與環境的接觸位移就能改變接觸力的大小，因此通過迭代機器人軌跡上單獨一段時間的偏移量可以修正機器人與環境的接觸力.在迭代的過程中，通過學習前期迭代的效果調整迭代策略，加快收斂，直到達到預期的軌跡，假設機器人和環境接觸時的狀態方程為

(5)

式中：A(t)為動態特征矩陣；B(t)為控制矩陣；C(t)為輸出矩陣；x(t) 為狀態變量；u(t)為輸入；y(t)為輸出力.可以將迭代算法設計為

(6)

(7)

因此式(6)迭代算法范圍為

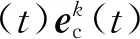
(8)

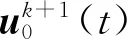
(2) 每一次迭代的初始條件一致，即

其中：x0為初始狀態；yd為初始期望輸出值.則算法單調收斂[16]，當k→∞時有：

yk(t)→yd(t), ?t∈[0,T]

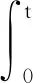
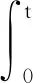
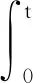
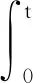
(9)

式中：τ，δ為0～t之間的變量.取Φ(t，τ)=exp[A(t-τ)]，則：

xk+1(t)-xk(t)=

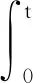
(10)

由于ek(t)=yd(t)-yk(t)，ek+1(t)=yd(t)-yk+1(t)，則：

ek+1(t)-ek(t)=yk(t)-yk+1(t)=

C(t)[xk(t)-xk+1(t)]=

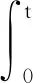
(11)

對式(11)整理可知，

ek+1(t)=ek(t)-

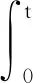
(12)

將式(8)的輸入代入式(12)，則第k+1次誤差為

ek+1(t)=ek(t)-

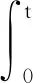
Γ(τ)eck(τ)]dτ

(13)

令G(t,τ)=C(t)Φ(t,τ)B(τ)Γ(τ)，有：

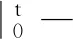
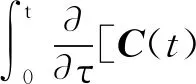
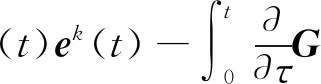
(14)

式(13)兩邊取范數：

‖ek+1(t)‖≤‖I-C(t)B(t)Γ(t)‖ ‖ek(t)‖+

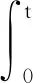
‖I-C(t)B(t)Γ(t)‖ ‖ek(t)‖+

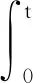
(15)

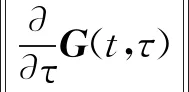
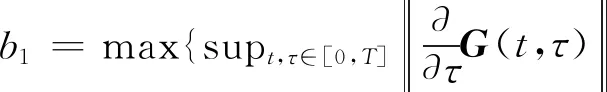
supt，τ∈[0，T]‖C(t)Φ(t，τ)B(τ)L(τ)‖}

其中T為迭代總時間.

定義1向量函數h:[0T]→Rn的λ-范數為

‖h‖λ=sup{exp(-λt)‖h(t)‖}(λ>0)

將式(15)兩端同時乘以exp(-λt)，則有：

exp(-λt)‖ek+1(t)‖≤

exp(-λt)‖I-C(t)B(t)Γ(t)‖ ‖ek(t)‖+

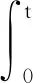
(16)

其中：

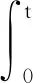
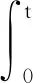
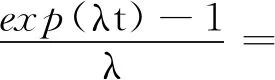
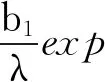
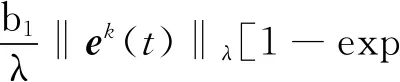
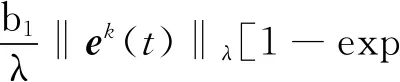
(17)

把式(17)代入式(16)中，則有：

exp(-λt)‖ek+1(t)‖≤

exp(-λt)‖I-C(t)B(t)Γ(t)‖ ‖ek(t)‖+

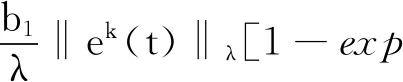
(18)

根據定義1可將式(18)化簡為

‖ek+1(t)‖λ≤‖I-C(t)B(t)Γ(t)‖ ‖ek(t)‖λ+

(19)

(20)

式中：

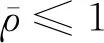
圖4 力控制算法Fig.4 Force control algorithm

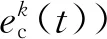
圖5 模糊算法流程圖Fig.5 Flow diagram of fuzzy algorithm

輸入變量和輸出變量的基本論域分別取：

(21)

隸屬度函數選擇三角形函數，在解模糊過程中，選用重心法，即

(22)

式中：w0為解模糊得到的輸出值；x為在論域v中的值；μN(x)為模糊集合N下對應x的隸屬度函數值.模糊規則選用：

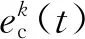
3 曲面輪廓恒力跟蹤實驗與分析

實驗采用安川機器人MH24，機器人在運動中控制器內置軟件MotoPlus接受外部 -10～10 V的模擬信號產生偏移，偏移位移方向與模擬信號符號一致，偏移位移與電壓絕對值大小成正比；六維力傳感器選用德國的ME-FKD40，由于傳感器末端安裝了探頭，因此采集六維力信號后，需要通過轉化矩陣得到沿著xT和yT方向的力，并對力的值進行標定，標定方法見文獻 [18]；采集的力信號通過上位機處理發送給倍福模塊，倍福模塊產生電壓模擬信號傳送給機器人控制器；曲面工件的尺寸如圖6所示，曲面的輪廓通過三維軟件中樣條曲線拉伸而成；曲面半徑R為34 mm，機器人運動的初始點為A，終點為B，機器人始終以1 mm/s的速度沿著xV方向移動；期望的力Fd為30 N.

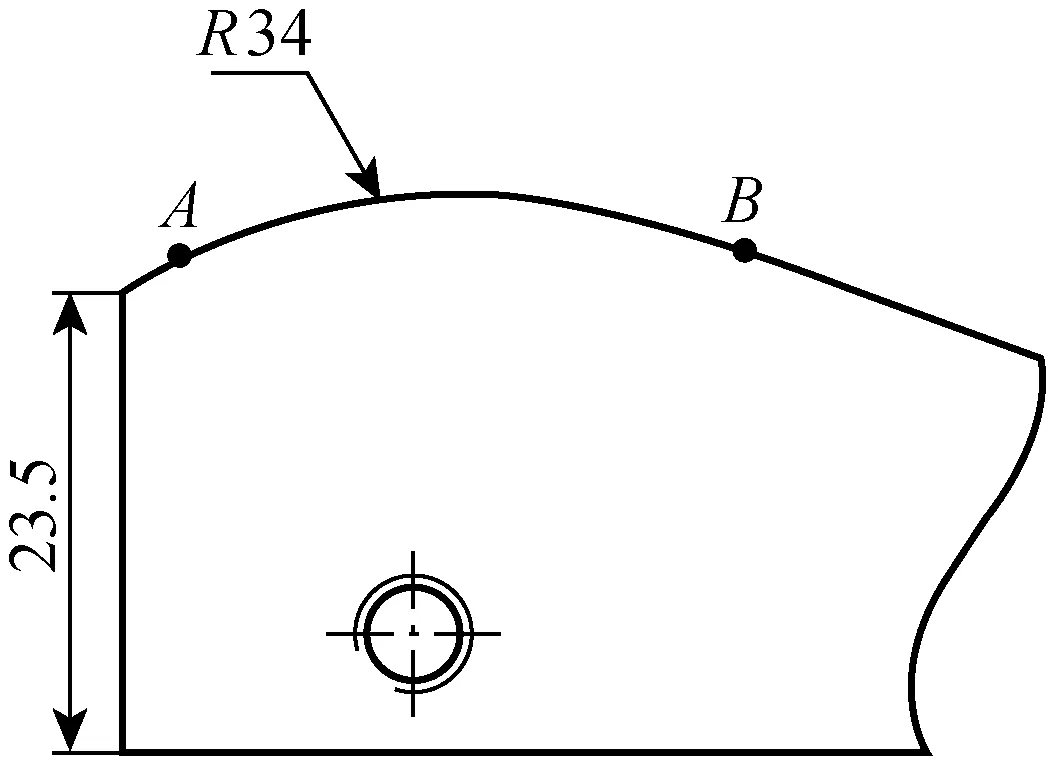
圖6 曲面工件(mm)Fig.6 Curved-surface workpiece (mm)

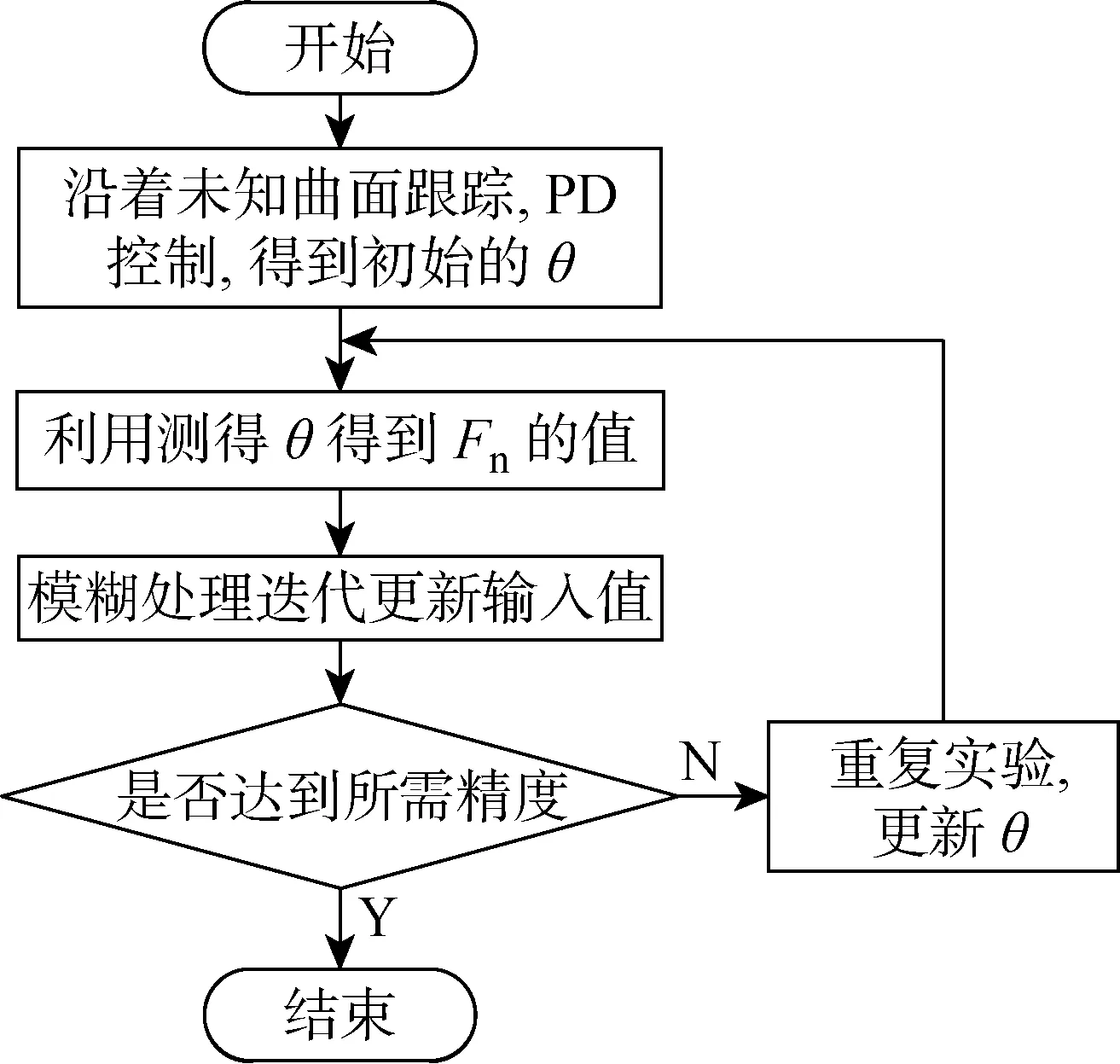
圖7 實驗流程圖Fig.7 Flow diagram of experiment

跟蹤實驗流程如圖7所示，在實驗過程中，機器人在運動過程中有以下幾種干擾：傳感器自身示數漂移干擾，底層算法插值運算處理時造成微小的丟步，運動過程中不確定性造成的干擾及摩擦力的干擾.為了避免干擾影響到整體的迭代效果，在迭代過程中每次改變力的大小不宜過大，迭代過程由前往后依次迭代.當實際接觸力F與期望力Fd之差ΔFe符號不同時，機器人偏移量方向是相反的，由于機器人的重復精度不高，同樣的迭代值下，每一次采集力的值一般會有較小的偏差，當ΔFe較小時，這種偏差會在重復實驗時迭代更新相同進給量卻造成相反的效果，加大誤差，故迭代過程只針對于 |ΔFe|>3 N 的時間段，設定每次迭代實驗力的閾值為10 N.

初始實驗PD參數中比例參數P=0.03，微分參數D=0.5，式(6)的kr(t)=3.2，kp(t)=3，kd(t)=1，采樣頻率為 1 000 Hz，檢測力信號中|ΔFe|>3 N的時間段，在超出閾值的時間段內，ΔFe的波形分為兩種情況，一種情況為力信號沒有回落，力信號一直增大或減小，為類型 I；另一種情況為力信號有回落，類似于拋物線，為類型 II.在迭代過程中，機器人在t時刻的總進給量等于t時刻進給量加上t時刻前進給量的總和，在更新當前時間段的偏移量時，為了保證后面時間段的偏移量不變，需要在后一段補償這段改變的值，因此對有回落過程的迭代更新方程為

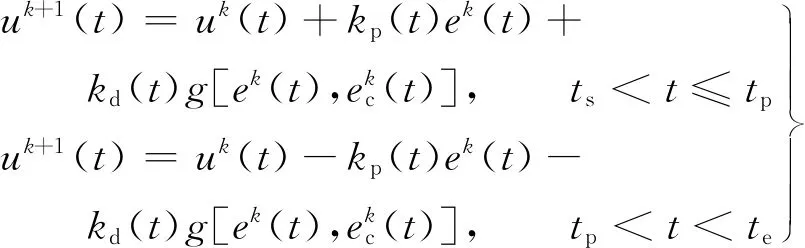
(23)

式中：ts為迭代開始時間；tp為ts到te時間段ΔFe絕對值的最大值對應的時間；te為迭代結束時間.迭代終止條件為：|ΔFe|<3 N.沒有回落過程時只更新不補償，迭代更新方程為

uk+1(t)=uk(t)+kp(t)ek(t)+

(24)

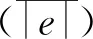
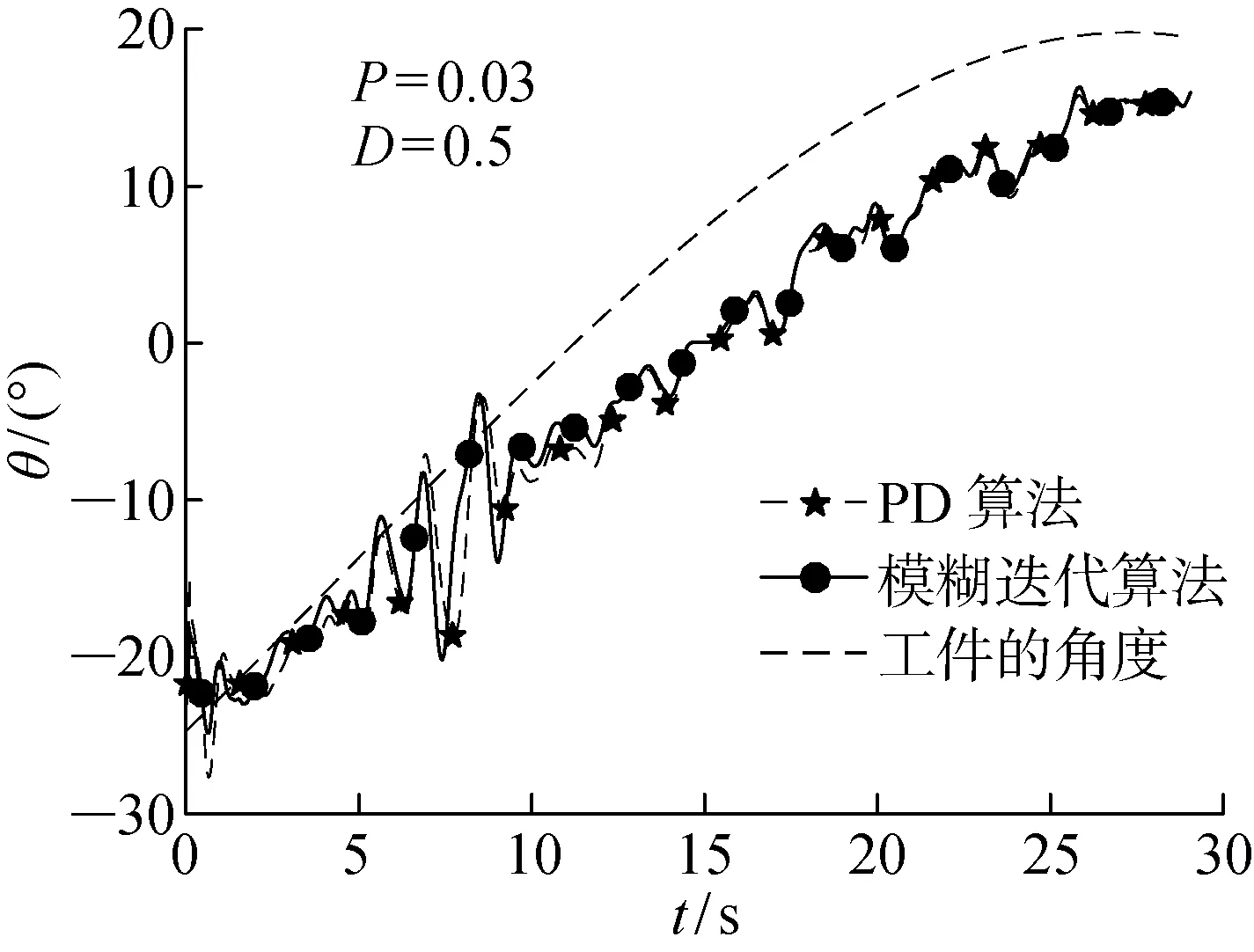
圖8 傾斜角對比圖Fig.8 Dip angle comparison chart

圖9 接觸力對比圖Fig.9 Comparison chart of contact force

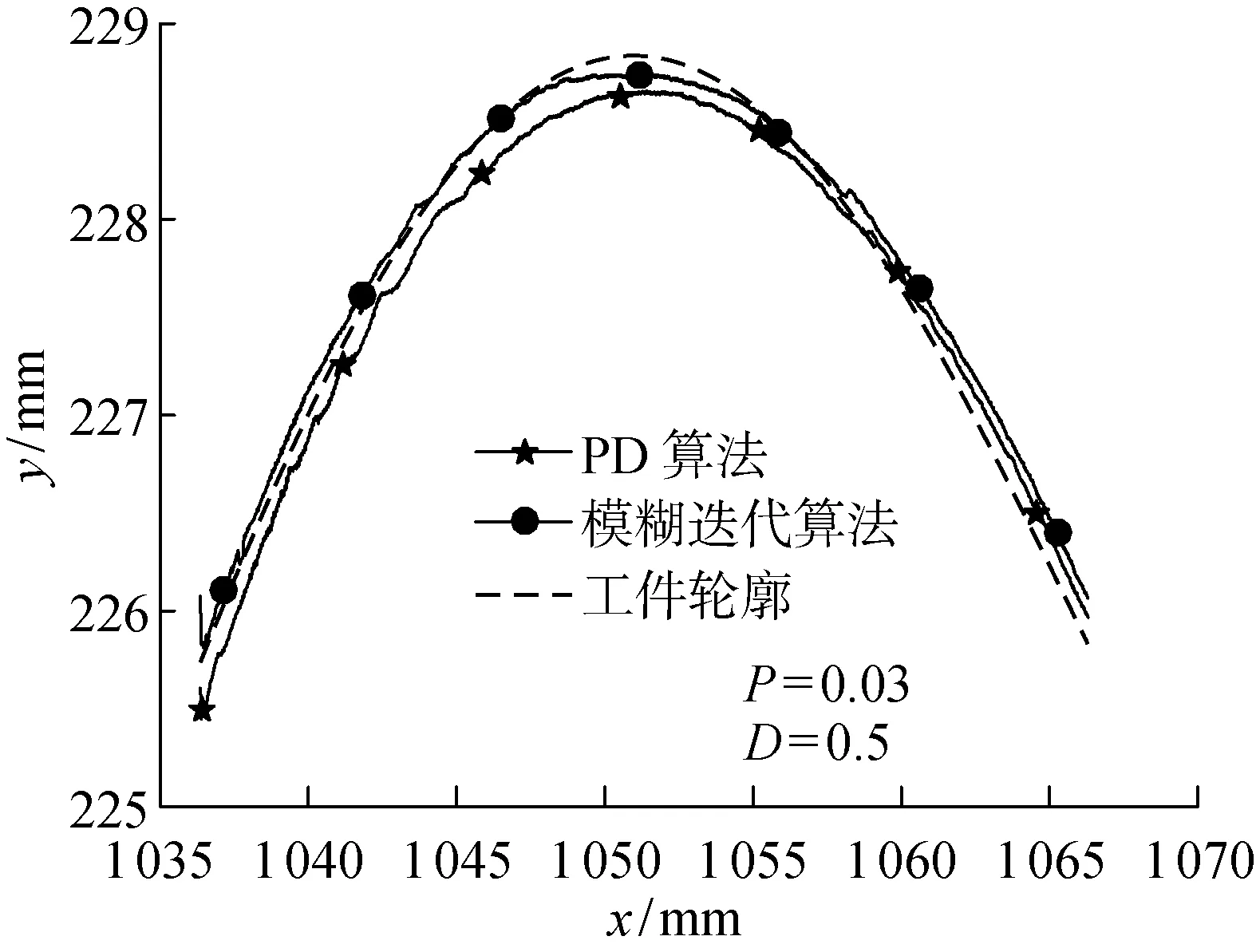
圖10 軌跡對比圖Fig.10 Trajectory comparison chart

實驗選取4段信號對模糊迭代算法和未進行模糊補償的迭代算法進行對比.未進行模糊補償的迭代次數分別為4，3，5，4次， 模糊迭代算法的迭代次數分別為2，2，3，3次.分別選取類型I和類型 II 兩種信號，對迭代過程進行對比，如圖11～14所示，在未進行模糊補償的迭代算法中每次迭代過程中根據力的大小選擇迭代量， 經過多次實驗后， 最終接觸力在目標范圍內，而在模糊迭代算法中，從第2次迭代開始利用前面實驗中迭代誤差補償后續實驗，加速收斂，如圖12和14所示.

表1 模糊迭代算法和PD算法對比

Tab.1 Comparison between fuzzy iterative algorithm and PD algorithm

算法|e|max/N|e|/Nσe/N|e'max|/mmPD算法8.53.24.20.25模糊迭代算法31.22.40.14

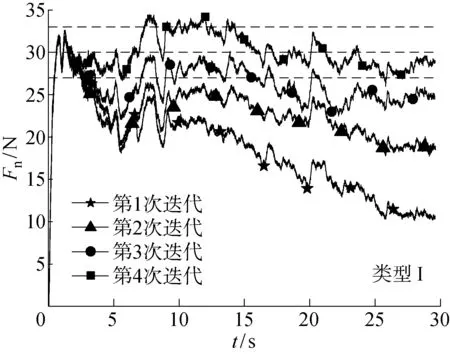
圖11 未進行模糊補償的迭代過程Fig.11 Iterative process without fuzzy compensation

圖12 模糊迭代過程Fig.12 Iterative process with fuzzy compensation

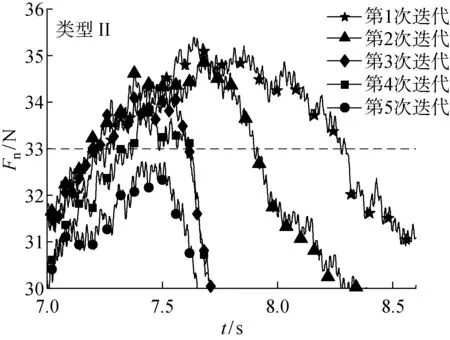
圖13 未進行模糊補償的迭代過程Fig.13 Iterative process without fuzzy compensation

圖14 模糊迭代過程Fig.14 Iterative process with fuzzy compensation

4 結論

(1) 對機器人末端執行器與曲面接觸進行受力分析，得到了各個坐標系之間的映射關系，構建了法向力和傳感器測量力之間的關系.

(2) 從理論上證明了提出的模糊迭代算法有界收斂，為實驗提供了理論基礎，實驗證明了算法可行性.

(3) 模糊迭代算法表現出較好的跟蹤性能，實驗得到法向力在期望值±3 N內波動.相比傳統的PD算法，接觸力誤差的均方差減少了42%，同時，曲面的跟蹤精度也得到了提高.

(4) 模糊迭代算法加速了收斂過程，與未進行模糊補償的迭代算法相比，在選擇的迭代周期內，迭代次數至少減少了1次.

利用模糊迭代算法得到精確的曲面輪廓為后續機器人打磨提供了較好初始軌跡.