一題一課小題大做

牛獻禮

【摘要】“一題一課”課程，就是教師通過對一道題或一個學習材料的深入研究，將這道題（或一則學習材料）拓展成一節課，讓其承載更多的教育價值。其順利實施的關鍵是教師對課程內容的教育價值的不斷追問與挖掘，以及對學情的準確把握。“一題一課”課程的內容取向基于教材而又不限于教材，可以是教材中富有內涵的習題、學生學習中的難點問題，以及其他有價值的學習材料等。在教學策略的應用上，更加注重以挑戰性的問題（或任務）引領學生圍繞知識的本質展開數學探究活動，并與“四基” “四能”的培養相結合。

【關鍵詞】一題一課 ? 價值定位 ? 內容選擇 ? 實施策略

“材料引起學習，材料引起活動。”學習材料是教與學的媒介，學習材料的選擇與使用往往會影響學生對數學知識的理解和數學素養的形成。許多教師在教學中一般不太關注教材習題等學習材料內涵的挖掘，或者蜻蜓點水、匆匆而過，滿足于問題答案的獲得，或者過于看重一節數學課解決題目的數量多寡，片面追求快節奏、大容量、高效率的所謂“高效課堂”。這兩種情況往往會造成學生習題做了不少，但若是碰到需要靈活、變式的問題就會不知所措、錯誤百出的現象。這歸根結底是因為沒有發揮好學習材料應有的教育價值，學生做的大量習題只是低水平的重復，很少體驗真正的“生活化”與“數學化”過程，導致學生的思維能力尤其是高階思維能力并沒有得到質的提升，核心素養的培育并沒有真正落地。

為此，筆者嘗試在教學實踐中開發“一題一課”課程，來拓展、豐富數學習題等學習材料的教育價值。所謂“一題一課”，就是教師通過對一道題（或一則學習材料）的深入研究，對其所涉及的知識內容進行拓展延伸，挖掘其內在的學習資源與線索，并科學、合理、有序地組織學生進行相關的數學探究活動，從而將這一道題（或一則學習材料）拓展成一節課，讓其承載更多的教育價值，以促進學生核心素養的形成與發展。

一、“一題一課”課程的價值定位與內容選擇

“一題一課”課程的順利實施，關鍵是教師對課程內容的深入研讀以及對學情的準確把握，并據此提煉出適切的課題。課題的選取應立足于培養學生研究數學、學好數學、用好數學的興趣;立足于數學思想方法的滲透，發展學生的高階思維能力，提升學生的思維品質;立足于豐富學生數學學習的方式，促進學生積累數學活動經驗;立足于拓寬學生的數學視野，體悟數學的價值。

“一題一課”課程作為數學基礎內容的有益補充，其內容取向基于教材而又不限于教材，注重結合學生實際去尋找數學核心素養的原始生長點，可以是教材中富有內涵的習題、學生學習中的難點問題以及其他有價值的學習材料等。選材宜精干，所涉及的主題應明確、具體，有利于學生深度參與到學習中去。

1.開發教材中的習題資源

小學數學教材凝聚了眾多專家學者對教育的認識、對數學的理解，是實現數學課程目標、實施數學教學的重要資源。教師應樹立正確的教材觀，尊重教材但又不“唯”教材，“基于”教材又能“創生”教材。對教材習題資源要進行深入研讀，既要讀懂每道習題的編寫意圖，把教材讀“厚”，整體考慮知識之間的關聯，挖掘習題中蘊含的數學思想方法;還應結合學生實際，將習題通過變式、引申、改造等方式，變封閉為開放、變單一為多元，充分發揮數學習題的教育價值，做到“題盡其用，小題大做”。

比如，“月歷表中的奧秘” “探秘三角板”等課題，都是將教材習題與探究學習相結合，指導學生通過合情推理去探索思路，推斷結果，發現結論，促使學生在“再創造”的過程中不斷迸發出學習熱情和創新思維的“火花”。有序思考、數學推理、幾何直觀一個不少，綜合地發生在探究性學習過程中，不僅加深了學生對相關知識的理解，同時也使學科核心素養的培育得到了有效落實。

2.研究學習中的難點問題

學習難點是在學習進程中學生感到難以理解、難以把握之處，常常表現為學習錯誤。學生在學習中出現的錯誤，展現了學生的真實思維歷程，也是寶貴的教學資源，在教學中同樣可以“小題大做”，進行合理的開發和利用。

比如，“長方形的周長和面積有何區別” “正方體的展開圖有哪些”等都是數學學習中的難點。教師可以對相關習題或材料進行深入研究，挖掘其內在的學習線索，并有序組織學生參與相關的數學探究活動。這不僅有利于突破難點、減少錯誤的發生，又能在學生收獲知識的同時，獲得數學思維的發展和活動經驗的積累。

3.補充有價值的學習材料

如前所述，教材是最重要的課程資源之一，但并不是唯一的課程資源。教師要增強課程意識，根據教材內容進行適度的延伸與拓展，增設一些有利于增強學習興趣、提升數學思維能力、落實數學核心素養培育的內容，拓展學生數學學習的空間。

比如，“好玩兒的‘對稱算式”一課，借助兩位數乘兩位數的“對稱”算式，引發學生的探究興趣，在探索驗證的過程中強化乘法口算、估算、筆算練習，提高學生的運算能力。在引領學生充分體會對稱之美的同時，經歷一次體驗深刻的“猜想—驗證—再猜想—再驗證”的科學研究過程，歸納出“對稱算式”中變與不變的規律，發展思維的嚴密性和推理能力，感受研究問題的方法，體驗數學學習的樂趣。

二、“一題一課”課程的實施策略

“一題一課”是以發展學生的數學核心素養為最終目標的，在教學策略的應用上，更加注重以挑戰性的問題或任務驅動學生主動去探究，一般以趣味性、實踐性、探究性的學習活動為主要形式。學生在啟發性問題的引領下主動參與、積極思考，在深刻理解知識本質的同時，感悟數學思想，積累數學思考與實踐的經驗。下面，以“探秘三角板”的教學為例加以說明。

北師大版數學四年級上冊“角的度量”單元中有一道思考題：利用一副三角尺你能畫出哪些不同度數的角？（如下圖）

此題內涵豐富，筆者沒有局限于解決這樣一個具體問題，而是深入挖掘三角板中有關數學思考的內容，努力放大題目的教育價值。教學中，讓學生圍繞“用一副三角板能畫出哪些不同度數的角”這個核心問題展開探究，指導學生從已有的事實出發，憑借經驗和直覺，通過合情推理去探索思路，推斷結果，發現結論，促使學生在“再創造”的過程中不斷迸發出學習熱情和創新“火花”。

【教學片段】

師：三角板是我們平時經常用到的一種學習用具，如果用數學的眼光來觀察，三角板中還有許多數學奧秘呢！今天這節課我們就來研究三角板中的奧秘（板書課題）。

師：你平時都用三角板做什么呢？

生1：畫線。

生2：畫角。

師（出示一塊含有30°角的三角板）：用這塊三角板你能畫出哪些度數的角？

生：能畫出30°、60°和90°的角。（板書）

師（出示另一塊含有45°角的三角板）：用這塊三角板畫角呢？

生：能畫出45°和90°的角。（板書）

師：用兩塊三角板分開畫角，一共能畫出哪幾個角呢？

生：30°、45°、60°、90°。

出示研究任務：用一副三角板拼起來畫角，還能畫出哪些度數的角？

要求：

（1）畫角時，兩塊三角板只能拼一次。

（2）在畫出的角中標出角的度數，并寫出是由兩個多少度的角拼成的。

（3）把用三角板拼起來畫出的角，連同用一塊三角板畫出的角，按照從小到大的順序排列起來。仔細觀察，你有什么發現嗎？

學生獨立思考、畫角，師巡視指導。然后，在指導小組交流的基礎上，進行全班交流。

生1：我們組一共畫出了10個角，從小到大是30°、45°、60°、75°、90°、105°、120°、135°、150°、180°。

生2：我們組還畫出了15°的角。（其他同學都很驚訝：怎樣畫15°的角呢？）

師：你是怎么畫的？能在黑板上畫一個15°的角嗎？

生2（邊在黑板上畫角，邊講畫法）：先畫出45°的角，再在里面畫出一個30°的角，剩下的就是15°的角。

（課件演示畫15°角的過程）

生3：我覺得還可以用60°和45°的角畫出15°，因為60°-45°也等于15°。

師：非常好！還能畫出別的角嗎？

生（搖頭）：沒有了。

師：好的，現在我們仔細觀察這些從小到大排列起來的角，有什么發現嗎？

生1：我發現它們都是15的倍數。（全班同學都表示贊同）

生2：我發現挨著的兩個角之間都是相差15°。

生3：不對，有兩個角相差的不是15°，150°和180°相差的是30°。

師：還真是這樣啊！前面這些角都符合“挨著的兩個角相差15°”這個規律，只是到了最后，規律“亂”掉了。看到這里，你有什么想法嗎？

生4（興奮地）：我有個想法！很可能有一個165°的角我們還沒有畫出來，如果畫出來了，150°+15°=165°，165°+15°=180°，每兩個角之間都會相差15°了。

該生的發言引起了班里部分同學的響應：對！對！有可能！

師：這倒是一個很有價值的猜想！（板書：猜想）你叫什么名字？

生4：我叫李晨星。

師：好，這個猜想就叫李晨星猜想（板書）！大家想想看，李晨星是瞎猜的嗎？他是根據什么提出的猜想？

生：他是根據前面“挨著的兩個角都是相差15°”這個規律提出的猜想，不是瞎猜的。

師：確實，李晨星的猜想是有依據的猜想。不過，數學上的猜想不見得都是正確的，還需要驗證。我們得想辦法把165°的角用一副三角板畫出來，而且是只拼一次三角板就能畫出165°的角。

全班學生又一次陷入了沉思，很快就熱烈地討論了起來。

生1：先畫出15°的角，再以一條邊為基礎，畫出150°的角，15°和150°加起來就是165°。

其他同學不同意生1的說法：只能用一副三角板拼一次呀！不能多次拼！

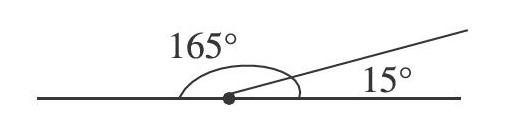
師：可不可以先畫出15°的角，再把15°角的一條邊延長，就得到了165°的角。（如下圖）

師：現在我們知道了，用一副三角板能畫出幾種不同的角來？

生：12種。

師：這么多種角，怎樣記不容易忘呢？

生：可以記它們的規律，兩個角之間差15°，比如我記住了90°，加15°就是105°，減15°就是75°，這樣就不容易忘了。

師：記住了規律，根據規律去找角就容易多了。現在，我們回顧一下剛才尋找角的過程，這12個角里面哪個角最不容易找到？

生：165°的角。

師：那我們是怎么找到165°的角的？

生：我們是先根據規律猜想到會有165°的角，再去畫一畫，去驗證。

師：沒錯！我們是先找到了這些角的排列規律，發現相鄰的兩個角都是相差15°，只有150°和180°相差了30°;接著，李晨星大膽地提出了一個猜想：可能我們漏掉了一個165°的角;然后，我們就想辦法去驗證，從平角里減去15°就畫出了165°的角。在這個過程中，你覺得什么最重要？

生：猜想最重要。

師：確實，猜想最重要，但猜想并不是“瞎猜”，而是從已有的事實出發，根據規律進行合情推理（板書：推理）。科學家們在科學研究中也經常用到這種思考問題的方法，比如：天文學家就是運用這樣的方法發現了海王星。

教師介紹科學史上“海王星的發現過程”：海王星最初并不是用望遠鏡發現的，而是在筆尖上被發現的。自從發現太陽系的第七顆行星（天王星）之后，天文學家便開始研究天王星運行的軌道，在研究過程中發現天王星實際運行的軌道和計算出來的軌道不完全一樣。天文學家推測有可能在天王星之外還有一顆未知的行星在干擾天王星的運行規律。但是，這顆新的行星究竟在哪里呢？天文學家運用數學的方法進行分析，用了2年多時間終于推算出了這顆新星的位置。后來，天文學家把望遠鏡指向用數學方法推算出的新星位置，在那里果真發現了一顆新的行星存在。這個“在筆尖上”發現的新星就是太陽系的第八顆行星——海王星。

師：李晨星同學很了不起！他發現了角度中的“海王星”！（同學們的掌聲又一次響起）

上述以解決問題“用一副三角板能畫出多少度的角”為載體的探究學習過程中，學生積極參與其中，經歷猜想、驗證等探索活動，在收獲經驗與感悟的同時，創新的火花不斷迸發。學生將畫出的角度從小到大有序排列，其實就是在進行理性思維;學生依據已有規律猜測出165°的角，實際上是在進行合情推理;“海王星發現過程的介紹”開闊了學生視野，增長了見識，讓學生更加深切地感受到數學的魅力與價值，數學核心素養的培育在上述探究性學習中得到了有效落實。

綜上所述，“一題一課”課程實施的主要策略在于，教師要不斷追問和發掘學習內容的教育價值，把教師理解的數學轉化為學生感興趣的數學活動，組織學生圍繞知識的本質內容展開數學探究活動，并與“四基” “四能”的培養相結合。