單一斷裂連續介質內地震發生的臨界條件*

劉培玄，李小軍，劉艷瓊

(1.北京工業大學 建筑工程學院，北京 100124；2.中國地震局發展研究中心，北京 100036；3.中國地震臺網中心，北京 100045)

0 引言

自古以來關于地震的起因就有多種說法，諸如地下雷、火山噴發、可燃性物質爆發燃燒、巖漿劇烈活動等。現在比較常見的地震成因學說有斷層成因說、巖漿沖擊成因說和相變成因說，其中斷層成因說最為人所重視。

地下巖石受到長期的構造作用積累了應變能，當積累的能量超過一定限度時，地下巖層突然破裂，形成斷層；或者是沿已有的斷層發生突然的滑動，釋放出很大的能量，其中一部分以地震波的形式傳播出去，形成地表震動，即彈性回跳理論(Reid，1910)，這是Reid(1910)研究1906年舊金山大地震發震斷層(圣安德烈斯斷層)的地表破裂所得到的結論。

地震描述可以等效為邊值條件下固體內部裂紋穩定性的力學問題(Rice，1976；Bigoni，2000)，在遠場邊界持續加載過程中，或地幔物質移動作用下，一定溫度下的巖石圈材料在裂紋處出現局部化變形。在分析域內，很多缺陷經歷不可逆的生長，如空洞和已有裂紋的匯合、位錯傳播、新的缺陷成核；同時不同類型的缺陷間會發生強烈的相互作用，促使位錯、裂紋快速進化、擴展，導致域內材料逐步劣化；裂紋周圍有限區域內積累的應變能突然釋放，促使裂紋失穩擴展，彈性回跳產生介質振動，以波的形式向四周傳播，隨后分析域進入調整期和新的積累期。

邊界應力持續加載是長時間的過程，失穩是瞬時發生的。關于裂紋穩定性定義，可歸結為：裂紋只有在外載荷不斷增加時，才能持續擴展，如果外載荷保持不變，裂紋就不繼續擴展，則可以認為裂紋狀態是穩定的；反之，若在外荷載不變情況下，裂紋持續加速擴展，則該裂紋狀態為不穩定(阿特金森，1992)。

設分析域中存在勢函數Π，在某一平衡狀態下有一任意小的擾動，此勢函數獲得一增量△Π，用Taylor級數在此平衡位置處展開：

(1)

式中：δΠ=0是平衡狀態保持穩定的充分條件。當ΔΠ＞0和δ2Π＞0時，系統是穩定的；當δ2Π＞0時系統是不穩定的；當δ2Π=0時，系統處于一個臨界點，系統有可能穩定，也有可能不穩定。

按照脆性失穩定義，地震發生是沒有前兆的，但由于人類知識的非完備性和地震發生的復雜性，應用GPS觀測裂紋的物理場，聯合斷裂力學方法，可以有效評估滑動斷層近期地震的危險性。本文從能量平衡原理出發，把地震觸發過程轉換為數學、力學中系統發生局部失穩問題，給出分析域內局部失穩臨界條件。計算了部分地震發震斷層的表面自由能，并給出了計算裂紋能量釋放率方法。

1 地震發生的臨界條件

(2)

固體本構關系形式為：

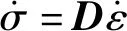
(3)

式中：D為介質的彈性剛度張量。

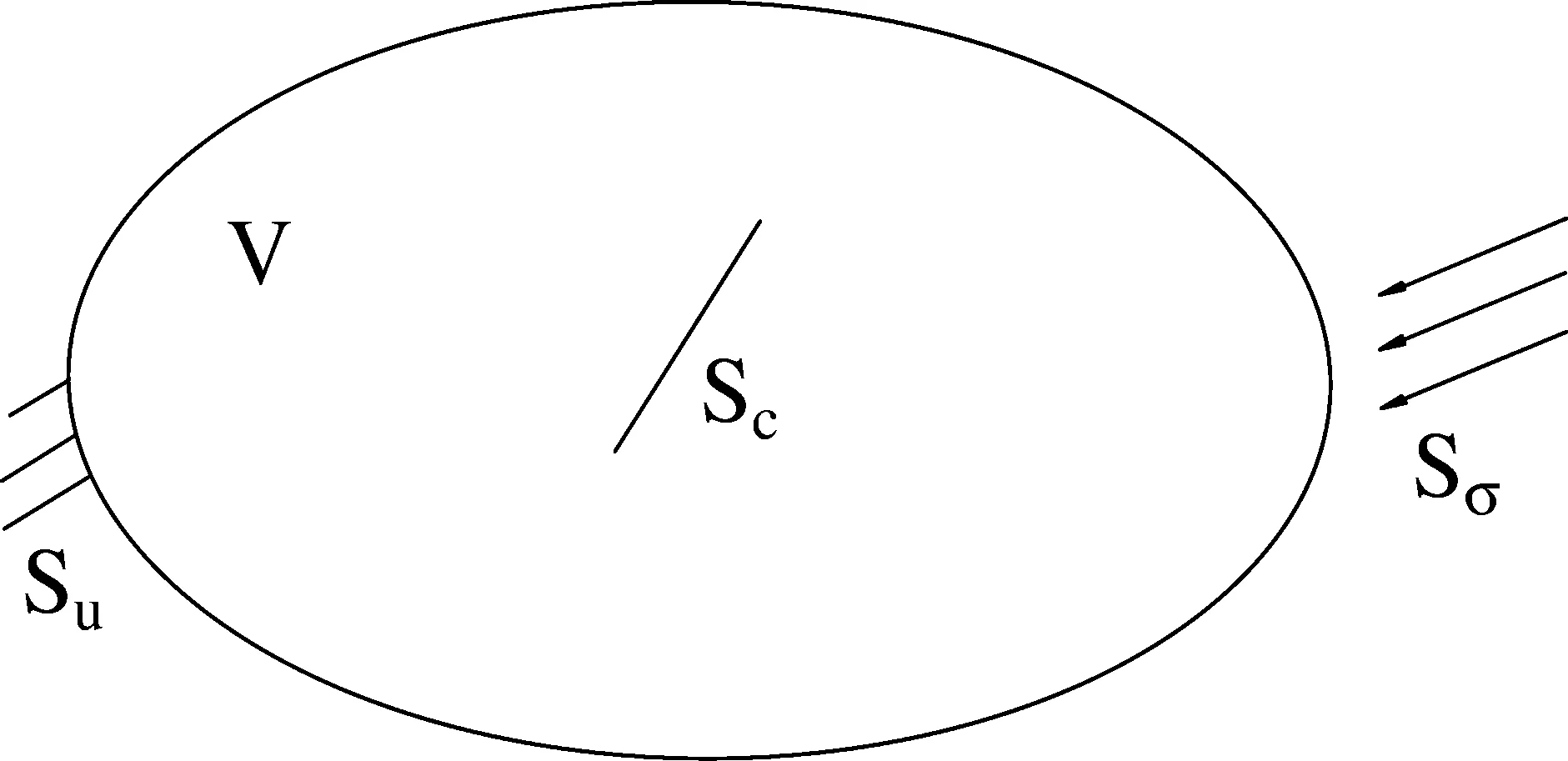
圖1 裂紋擴展和失穩破裂過程模型Fig.1 Model of crack propagation and instability rupture process

在擬靜力加載條件下，建立滿足式(2)和(3)初邊值條件的介質出現裂紋擴展和裂紋失穩破裂過程模型(圖1)，其中包括擬靜力應變能積累過程和系統失穩的地震過程。

由于裂紋存在，固體內部位移場為u=u+[[u]]HS，HS為裂紋處的階躍函數，裂紋處作用力為φc，相應的勢能原(Washizu，1982)為：

(4)

δΠ=0，即有：

(5)

式(5)左邊前3項分別對應平衡方程、應力邊界條件和位移邊界條件。筆者關注的是第四項，只有符合裂紋擴展條件，即：φc=n[σc(Gc)]，才存在裂紋穩態擴展，即：

σ(G)-σc(Gc)=0

(6)

式中：G是裂紋擴展的能量釋放率；σ(G)是以G表述的應力；Gc是裂紋表面自由能，其值為2Γ；σc(Gc)是以Gc表述的材料破壞應力。

式(6)也可以采用應力強度因子K和J積分來表述，三者存在確定的關系，且在擬靜態過程中等效。需要說明，在經典斷裂力學中，裂紋尖端的應力具有奇異性，式(6)中的σ(G)改為G(σ)可能更好理解；但在分子動力學分析中，材料破裂的本質是原子鍵的斷裂。

由式(1)知，臨界穩定性條件為：

(7)

對于巖石圈材料，σc(Gc)在裂紋擴展過程中有所變化，在均勻脆性材料中，僅當δσc(Gc)=0時，才能與線性斷裂力學一致；一般地，當分析域內存在一裂紋時，不管是基于線性還是非線性斷裂力學觀點，裂紋尖端存在應力集中區，裂紋附近區域積累的應變能消耗就會集中在裂紋擴展上。

域內剛度(式(7)第一項)會從加載階段進化為彈性卸載分叉狀態，即式(7)右邊第一項為0。因此裂紋失穩擴展的臨界條件為：

(8)

把裂紋剖分為有限個子段Sci，上式轉化為：

(9)

當子段足夠小，且能識別裂紋尖端時，式(8)等價于：

nδ[σ(G)-σc(Gc)]·δ[[u]]=0

(10)

由式(6)可知：

(11)

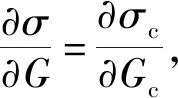
(12)

按照斷裂力學之能量釋放率的定義，無論裂紋擴展沿自身平面還是轉向，其尖端擴展均采用了移動坐標規定，即δSc與δ[[u]]反向(李世愚等，2010)。考慮特殊向量δ[[u]]=-g和δSc=h?n，其中，?h≠0，?g≠0,?n∈|n|=1,合并g·h=D，則式(12)變化為：

(13)

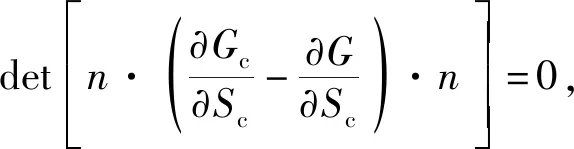
特殊情況下，當僅考慮3種基本斷裂情況時，失穩擴展臨界條件為：

(14)

失穩擴展條件為：

(15)

由此不難得出，若分析域內能量釋放率G與表面自由能Gc線性變化時，失穩擴展條件為Gc＞G。在滿足式(15)時，結合式(2)可判斷由新生破裂或斷層膠結后的再次破裂的地震發生。

2 能量釋放率與裂紋表面自由能

2.1 能量釋放率G

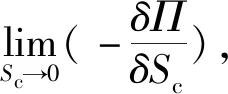
Gi=K2i/E′i,i=1,2,3

(16)

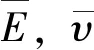
應力強度因子K僅與外加荷載形式、擴展路徑和巖體裂紋幾何形狀有關，具體見《應力強度因子手冊》(中國航空研究院，1981)。但對巖石介質來講，其中的裂紋不僅尖端存在應力，在裂紋面也存在著由摩擦律確定的應力，再加上巖層變化與缺失、巖體的微觀結構與組構、構造環境與自然環境等因素的影響，得到一段斷裂可靠的應力強度因子K也是不易的。

2.2 裂紋表面自由能Gc

表面自由能Gc定義為2Γ，Γ是形成單位裂紋所需的能量。一般應用Gc和Kc的關系進行轉換，對于3類基本斷裂形式有：

Gci=K2ci/E′i,i=1,2,3

(17)

到目前為止，巖石斷裂韌性Kc試驗已使用了許多不同的試件類型及方法，其結果相差很大，意味著測出的結果通常不能真正代表材料的性質。因此，國際巖石力學學會(ISRM)測試方法委員會推薦了試驗方法，盡管方法也有上述問題，但仔細的試件制作、加載條件和測量精度要求，對定量的比較應用還是具有重要意義的。

3 發震斷裂的表面自由能和能量釋放率估算

3.1 發震斷裂的表面自由能估算

現今巖石圈內的材料是不同時期的產物，不同地質構造期內主營造力不同，環境溫度、濕度、壓力不同，材料的結晶、解理等物理和化學過程存在差異，致使材料的結構和組構不同，造就了不同規模斷裂、裂隙、裂紋分割巖石圈內的不同級別的塊體。

不同規模斷裂形成是由熱過程或力學過程引起的，其擴展特性與系統內存儲的能量、巖體和裂紋特性相關。抵抗裂紋擴展的表面自由能不僅與裂紋尖端的微觀結構和組構特性直接相關，還與溫度、流體、應力腐蝕相關。在有壓流體作用下，活性物質的遷移會導致裂紋尖端的微觀結構變化；表面自由能除涉及到的機械能部分外，還有特定環境下裂紋尖端的塑性功、熱能、化學反應能量等。

因此，得到較可靠的Gc是困難的；但是應用已發生的地震參數和彈性斷裂力學可估算Gc。假定一次地震的地表破裂有效長度為L，應力降為Δσ，則破裂上位移分布為：

(18)

式中：μ和υ分別為巖石介質的剪切模量和泊松比，這里分別取35 GPa和0.25(阿特金森，1992)。

假定地震為中間破裂向兩側擴展，最大位移dmax在斷裂的中心，表面自由能為(阿特金森，1992)：

(19)

采用Mohammadioun和Serva(2001)研究中的地震資料和近年來發生的典型破壞地震資料(張勇等，2013；Shenetal，2017；申文豪等，2019)，計算了走滑、逆和正斷裂的Gc，見表1～3。如果考慮地震破裂發生在地殼淺層，比如巖石圈厚度為50 km的10 km處，那么表中Gc加權因子為5左右(阿特金森，1992)。由表1可知，走滑斷裂引起的地震表面自由能最大為5.2×107J/m2。由表2可知，逆斷裂引起的地震表面自由能最大為5.4×107J/m2。由表3可知，正斷裂引起的地震表面自由能最大為4.5×107J/m2。

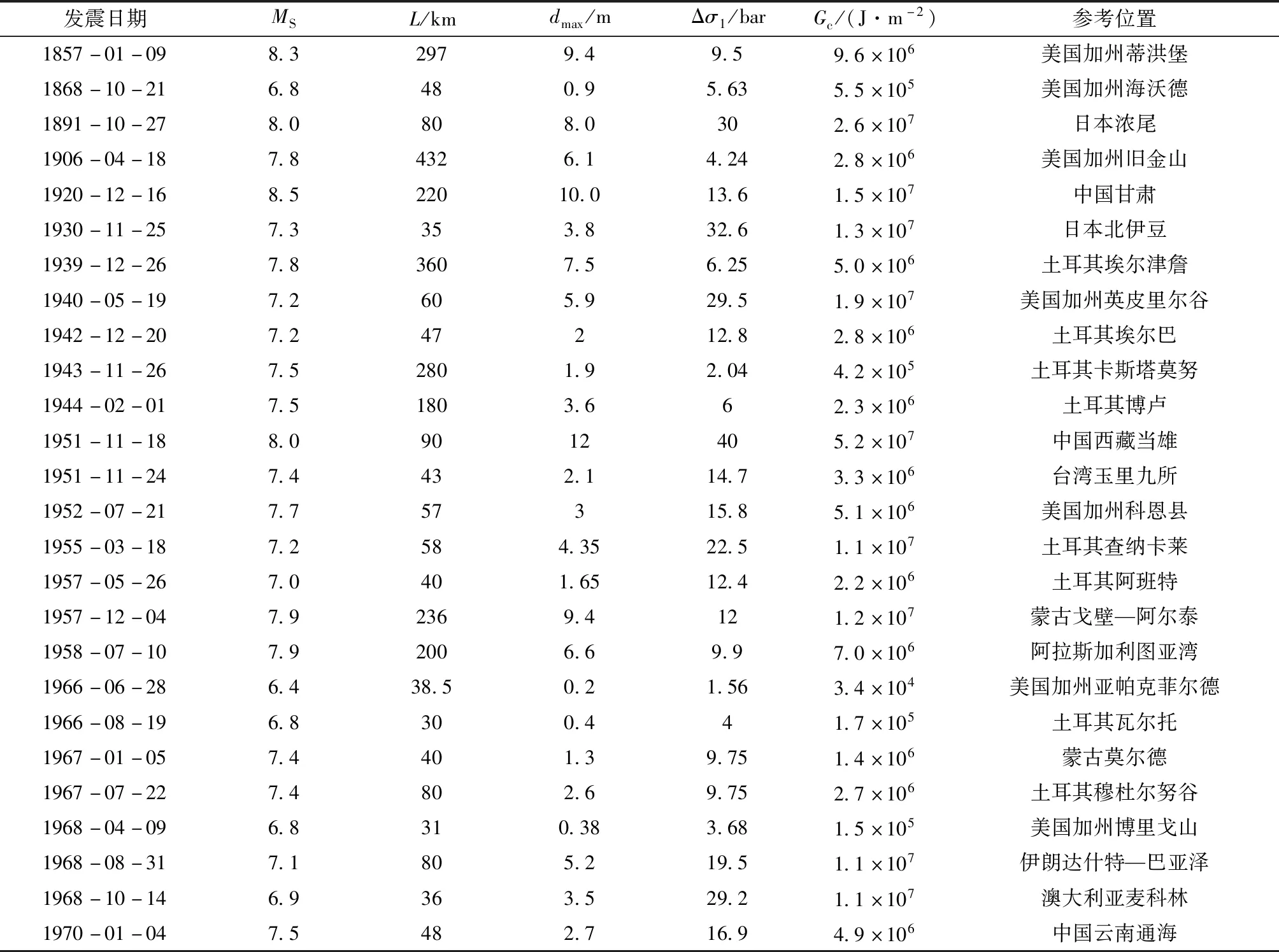
表1 地震震源參數(走滑斷裂)Tab.1 Earthquake source parameters(strike-slip fault)

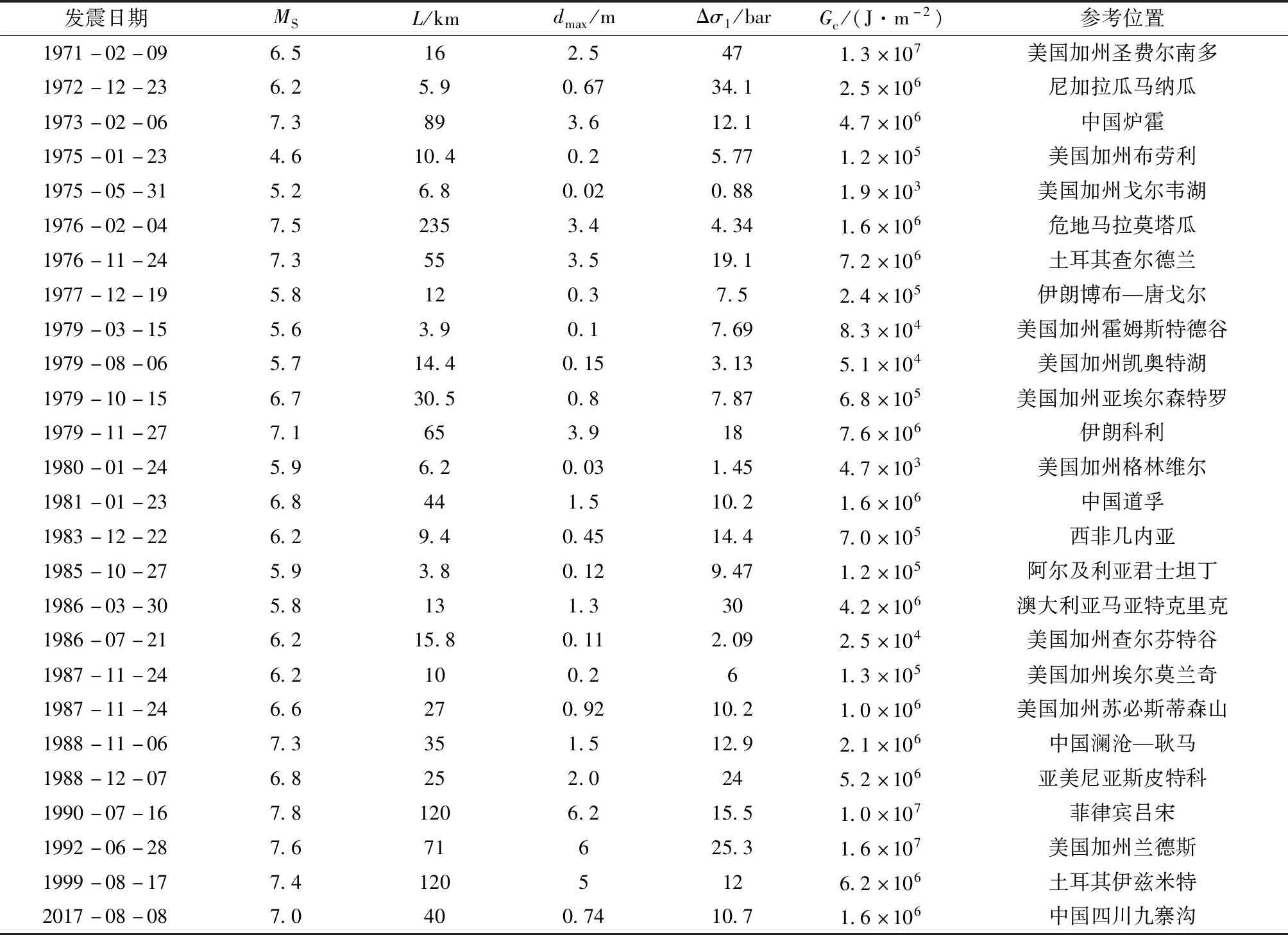
續表1

表2 地震震源參數(逆斷裂)Tab.2 Earthquake source parameters(reversed fault)

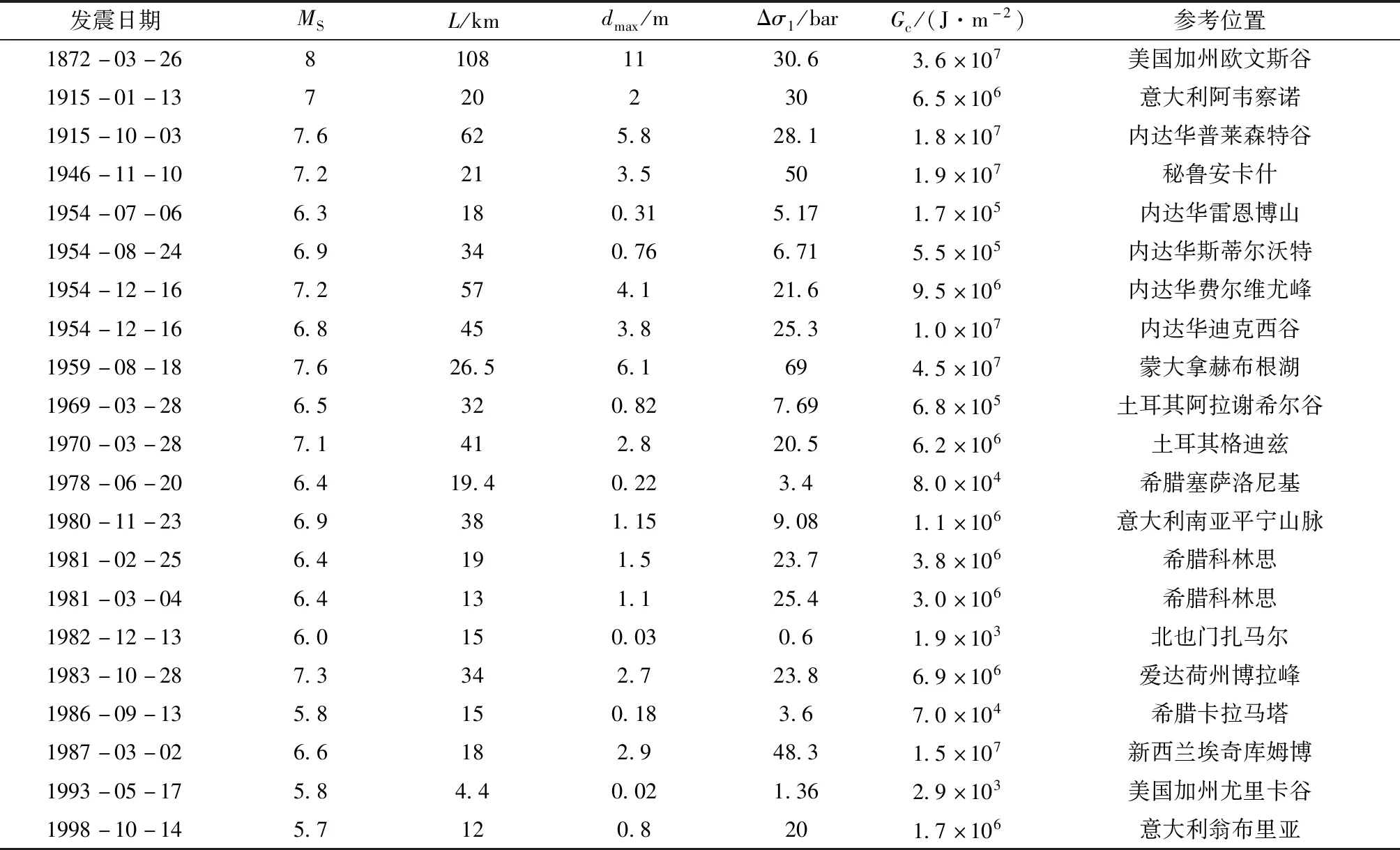
表3 地震震源參數(正斷裂)Tab.3 Earthquake source parameters(normal fault)

3.2 發震斷裂的能量釋放率估算

地質體內裂紋尺度跨越微米到千千米之間，求解發震斷層(段)的G值，目標是分析域內裂紋尺度最顯著的幾條。當裂紋尺度與分析域尺度之比很小時，即：相應塊體分析域內存在一條或多條較短的斷裂時，可以采用域內損傷來處理，得到等效的彈性參數(寧建國等，2012)。

在分析域內，以有限個跨越斷裂的GPS值和局部構造應力場方向，對K進行求解。具體的變分原理為：

(20)

式中：α是罰函數，Π見式(4)，域邊界處的測點GPS觀測值作為位移邊界。

遠離裂紋的位移采用有限單元標準離散，裂紋尖端采用半解析形函數，得到計算域內整體有限元格式，求解以上方程得到位移場、應變場和K(董玉文，2008)，通過式(16)得到斷裂現階段的G值。

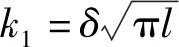
按照脆性失穩定義，地震發生是沒有前兆的，但實際上地震的孕育和發生是一個復雜的過程，加之對于地殼介質的多相性、斷裂深部幾何構造與物理特征、區域構造運動的非均勻性等的認知的非完整性，故不能排除一些地震存在的征兆。

此處不討論地震將要發生的前兆，而是限定在區域內幾條活動斷裂，進行長時間(最好10年以上)的跨斷層GPS觀測(張國安等，2002；王瑞平，潘振生，2009；吳云等，2003)以及應變和應力實地測量(陳啟林等，2002；胡衛建等，2002；謝富仁等，2005)，量化沿斷層位移場、應變場和應力場的變化，確定閉鎖范圍的尺度，估算未來發生地震的震級；在進行長時間沿斷層的考察時，尤其要注意裂紋(或閉鎖范圍)尖端的位移變化，比如出現鼓包、凹陷和剪切裂紋等局部現象，當局部變形變化劇烈時，理論分析能量釋放率和斷裂表面自由能之間的關系，評估地震發生的可能性。

4 結論與討論

本文針對單一裂紋連續介質內地震發生的臨界條件、能量釋放率與裂紋表面自由能進行了理論分析，得到的主要結論如下：

(1)從能量原理出發，可把地震觸發過程視為數學、力學中系統發生局部失穩問題，并推導出分析域內局部失穩臨界條件為新生破裂或斷層膠結后的再次破裂，即地震發生條件。

(2)基于線性斷裂力學理論，統計分析了震源參數較全的一些歷史地震發震斷層的表面自由能，結果表明，走滑斷裂、逆斷裂、正斷裂引起的地震表面自由能最大分別為5.2×107J/m2，5.4×107J/m2，4.5×107J/m2。

(3)依據應用勢能原理，提出了一個由GPS臺網觀測數據確定斷裂能量釋放率的計算公式，為進行特定斷裂近期發生地震的可能性的判定提供了方法。

按照脆性失穩定義，地震發生是沒有前兆的。然而由于對地殼介質、斷裂深部幾何構造、區域構造運動認知的非完整性，不能排除一些地震會存在前兆。通常地震發生前，發震斷裂區域范圍內的位移場會產生變化，尤其在斷裂端部產生諸如鼓包、凹陷和裂紋等局部位移異常，當這些異常顯著時，可由理論分析能量釋放率和斷裂表面自由能之間的關系，判斷地震發生的可能性。GPS是位移場觀測的一個重要工具，它不僅能給出斷層附近的位移場分布，還可以分析閉鎖區域的范圍和能量積累，這為本文方法的應用提供了數據基礎。

本文計算應力、裂紋能量釋放率等的方法基于實驗室中得到的材料和巖石力學原理公式，而實際中的地表斷層的大規模運動、物質遷移和地震現象與實驗室中的實驗有著顯著的不同。目前的實驗還無法完全真實地模擬出真實地震的應力積累和發生機制，這也是當前地震研究的難點之一。本文理論計算與實際的差異除了來自于數據來源的可靠性、模型的不確定性等因素之外，實驗中的巖石材料與實際地殼斷層的本質區別也是重要的因素。因此，本文提出的判定斷層危險狀態的方法可以作為一種思路的嘗試，但要形成完整理論體系、真正在實際地震中得到應用，還需要對模型、公式做大量的改進。