CG-5重力儀一次項系數變化特性分析及其對觀測數據的影響研究*

黃江培，王青華，徐聲鑫，劉 東，曹 穎，邱 奎

(云南省地震局，云南 昆明 650224)

0 引言

高精度的重力觀測資料能夠較好地反映伴隨活動斷層的物質遷移和構造變形所引起的地表重力變化(祝意青等，2015，2018a；王同慶等，2017)，在地震中長期預測中效果顯著(祝意青等，2018b)。云南省于20世紀80年代就開始進行地震相對重力觀測，至2018年已經實現云南省行政區域觀測全覆蓋。

加拿大SCINTREX 公司生產的CG-5相對重力儀，標稱測量精度達到5×10-8m/s2，讀數分辨率達1×10-8m/s2，同時具有較高的自動化程度(郝洪濤等，2011，2016)，被廣泛運用于中國礦產探測及地震科學研究。研究人員多年來對觀測數據進行分析發現，CG-5重力儀一次項系數在不同觀測周期均有所不同，且不同儀器的變化趨勢及數值均有差異(馮建林等，2017；梁偉鋒等，2015)。目前中國地震局重力學科組(以下簡稱“重力學科組”)每2～3年組織一次全國性的長基線標定，各個測區在每個測量周期開測之前也會進行短基線標定，用于修正儀器的一次項系數。長基線標定可以滿足測值跨度的要求，但在時間維度上無法滿足一年2期的修正要求；短基線標定在時間上能基本滿足每期一次修正要求，但是云南短基線標定300×10-5m/s2的測值跨度在空間上無法滿足整個云南測區的測值段跨度修正要求。一次項系數對觀測數據的影響為系統誤差，因此可通過數據分析處理進行消除。

本文收集2015年3月至2018年3月云南區域共7期相對重力觀測數據，基于同時同地觀測的2臺重力儀不存在觀測物理量偏差的原理，利用線性回歸分析獲取其在每期觀測中的一次項系數變化差異，并對在一個觀測周期內不同時間段及不同測值段的變化特性進行分析，計算一次項系數修正值，最終獲取每期觀測時儀器一次項系數的最或然值，并分析其對地震觀測數據的影響。

1 數據與方法

1.1 觀測數據

相對重力測量采用周期性復測的形式進行觀測，一年觀測2期，測區上半年觀測于每年的3—5月完成，下半年于7—9月完成。2017年以前云南省地震局主要承擔滇東北、滇中、滇西南的相對重力觀測任務，2018年以后，重力學科組根據屬地原則進行測區調整，云南省地震局除了接手中國地震局第一監測中心在云南區域的測量任務外，還在空白區域增設測點，實現了相對重力觀測對云南省行政區域的全覆蓋，監測區域如圖1所示。

2014年云南省地震局引進2臺CG-5相對重力儀(編號分別為CG-1169，CG-1170)，用于相對重力觀測。洪濤等(2016)對2014年的觀測數據進行研究，結果表明2臺儀器的一次項系數存在變化差異。云南高山谷地縱橫交錯，重力測值跨度超過1 000×10-5m/s2，微小的一次項系數偏差會對計算結果造成較大的系統誤差，直接對地震趨勢分析造成影響。

根據《國家重力控制測量規范》(GB/T 20256—2006)規定，段差是重力測量中相鄰2個點間的重力差值，互差為2臺儀器同時觀測同一段差之差。根據《地震重力測量規范》(國家地震局，1979)規定，G型相對重力儀的一次項系數一般每隔3年須使用長基線標定一次。因此，重力學科組于2014年底組織全國地震系統內的重力儀進行長基線標定，其中云南省地震局2臺儀器一次項系數標定結果分別為CG-1169：1.000 006，CG-1170：1.000 031。利用該標定結果，對2015年3月至2018年3月共7期的觀測資料進行計算，統計分析2臺儀器測值互差及段差的關系，結果如圖2所示(圖中橫坐標表示2點之間的重力差值，簡稱為段差，縱坐標表示2臺儀器同一段差的差值，簡稱為互差)。

從圖2可以看出，在2015年3月觀測時，2臺儀器互差隨段差的變化成離散狀態，總體呈正態分布，符合偶然誤差的分布規律；2015年8月至2017年8月2臺儀器互差隨段差的變化趨勢逐漸明晰，但是絕對差異值均在規定的限差(30×10-8m/s2)之內，到2018年3月時2臺儀器互差與段差的關系總體已經成線性關系，差異值已經突破100×10-8m/s2，這種情況下，繼續使用2014年長基線標定的一次項系數進行計算必然會導致較大誤差，因此必須進行一次項系數修正。因為互差隨段差變化趨勢總體呈成線性關系，可以采用線性回歸分析的方法進行分析，首先建立數學模型。

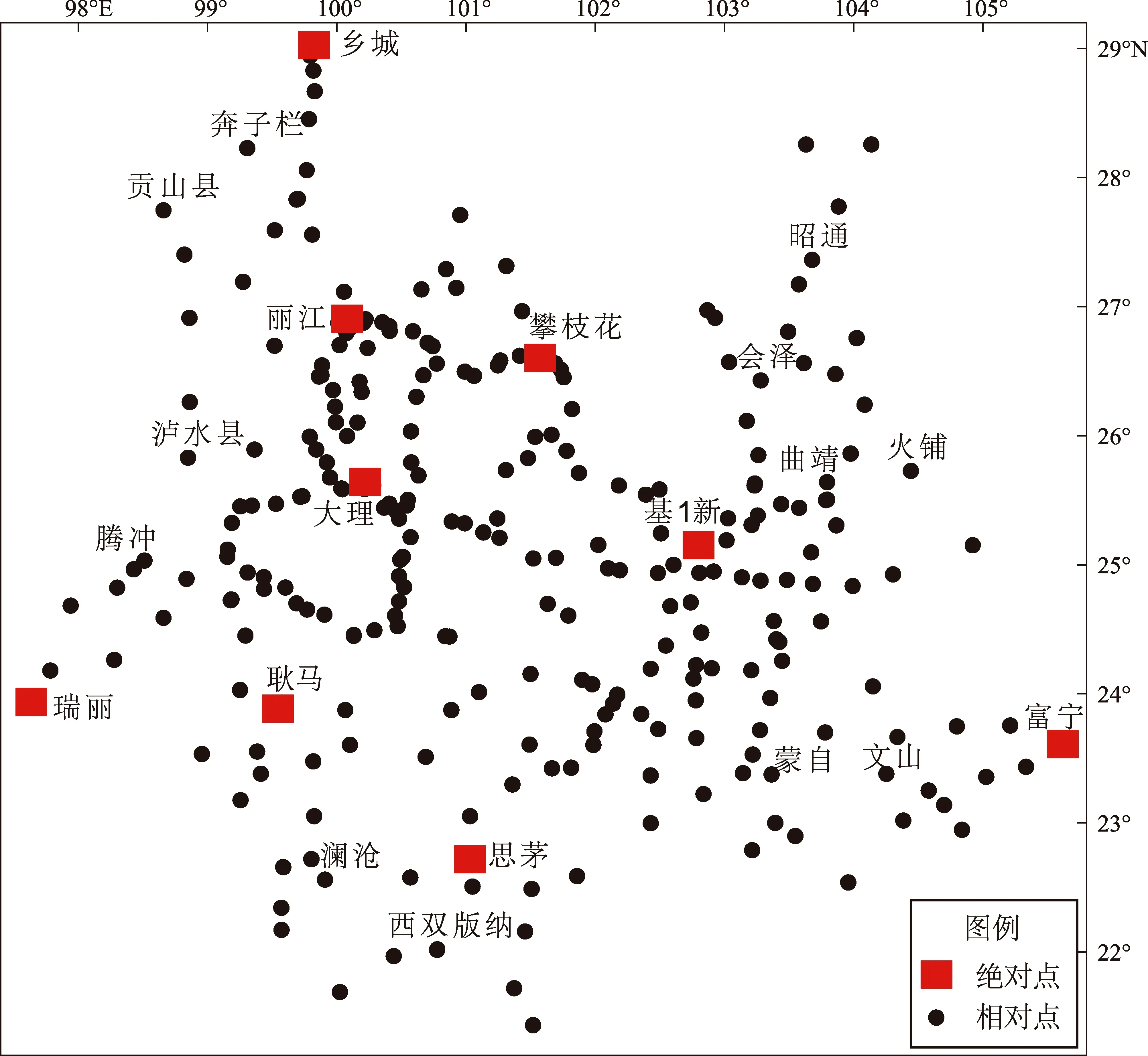
圖1 云南省相對重力觀測點分布圖Fig.1 Map showing relative gravity observation sites in Yunnan province

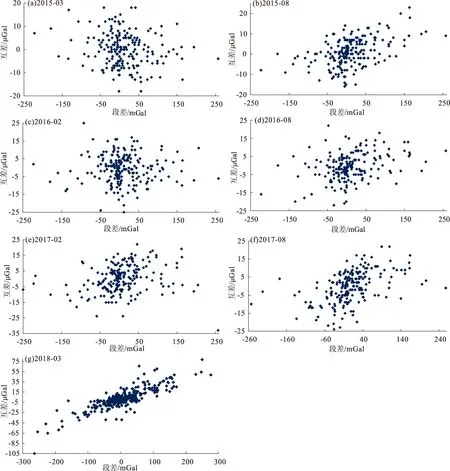
圖2 不同觀測周期2臺儀器互差與段差關系Fig.2 The relation diagram of mutual difference and segment difference between two gravimeters in different observation periods

1.2 數學模型

根據CG-5重力儀出廠參數，其非線性系數已經調整為0，觀測值僅考慮其一次項標定系數即可。在不考慮偶然觀測誤差的情況下，某個測點上的讀數值數學模型為：

F(Xi)=E(Xi+x0+δ漂+δ固+t溫+p壓+h高)

(1)

式中：E為一次項系數；Xi為該點重力值；x0為儀器零重力值讀數；δ漂為零漂改正；δ固為固體潮改正；t溫為溫度改正；p壓為氣壓改正；h高為儀高改正。

CG-5為相對重力觀測儀器，式(1)中x0為未知數，如果沒有聯測基準點，在某一個測點上的儀器讀數不具備物理意義，但是對相鄰2個觀測點進行差值計算后消除x0，剩下的各項改正均可通過觀測其他物理量或經驗公式獲取，最終結果即為2個測點的段差。

因此，CG-5重力儀對相鄰2個測點的段差觀測值數學模型可簡化為：

F(Xij)=(E+ΔE)(Xi-Xj)

(2)

式中：ΔE為一次項系數差異。

由于2臺儀器同時同地觀測，其觀測結果不存在物理量差異，如果觀測二者存在系統誤差，可以判定為是由于一次項系數差異ΔE引起的，其數學模型可表示為：

DXij=(E1+ΔE1)(Xi-Xj)-(E2+ΔE2)(Xi-Xj)=ΔE12(Xi-Xj)

(3)

其誤差方程為：

(4)

將7期觀測數據分別帶入式(4)，利用經典平差方法結算，計算出每期2臺儀器一次項系數變化的差異ΔE見表1。

從表1可以看出，2臺儀器的一次項系數變化差異在各期均不一致，隨著時間推移總體呈增大趨勢，在2018年3月觀測時，已經達到萬分之二以上，對重力值跨度超過1 000 000×10-8m/s2的云南區域影響明顯。

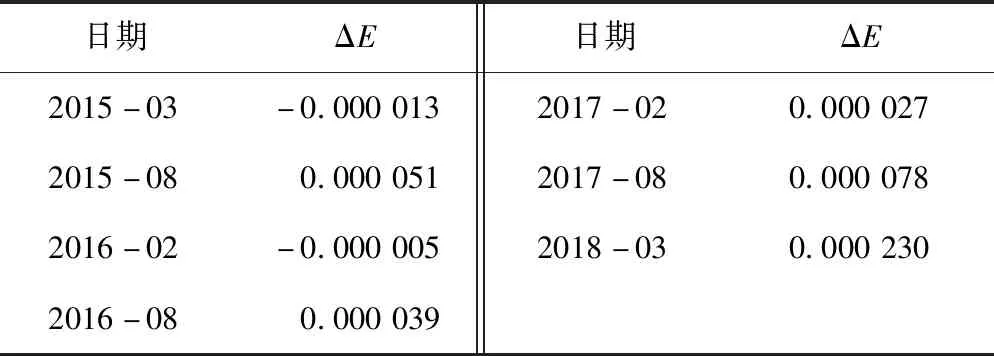
表1 各個觀測周期內2臺儀器的一次項系數變化差異Tab.1 Differences of primary term coefficient between two gravimeters in each observation period

1.3 在同一觀測周期內一次項系數隨時間變化分析

每一期觀測時，重力儀一次項系數與上期均有變化，且2臺儀器變化是存在差異的。完成一個觀測周期大概需要60～100 d，為了分析此期間內2臺儀器的一次項系數的變化差異特性，本文以差異較為明顯的2018-03期為例，在一個觀測周期內，以15 d為間隔，對2臺儀器的一次項系數差異進行計算，結果如圖3所示。

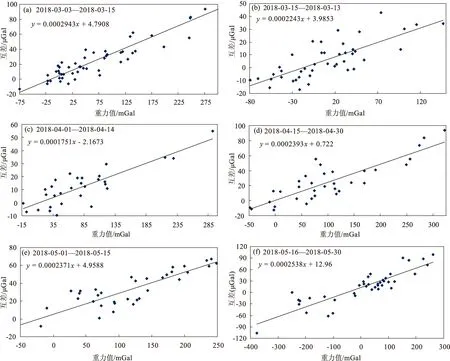
圖3 同一觀測周期內不同時間段2臺儀器一次項系數差異Fig.3 Differences of primary term coefficient between two gravimeters in different time periods in an observation period

從圖3可以看出，由于總樣本被拆分成多個小樣本，數據量減少，觀測誤差對回歸分析結果影響增大，但是在一個觀測周期的不同時間段，2臺儀器一次項系數差異總體趨勢是一致的，不同時間段變化并不大。通過線性回歸分析，不同時間段2臺儀器一次項系數差異如表2所示。

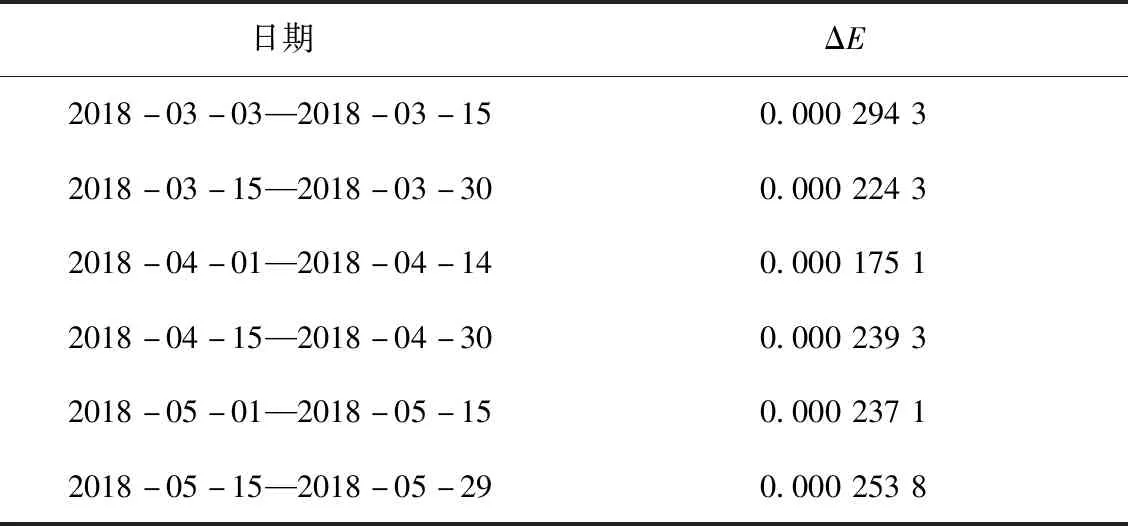
表2 同一觀測周期內不同時間段的一次項系數變化差異Tab.2 Differences of primary term coefficient between tow gravimeters in different time periods in an observation period

從表2可以看出，在一個觀測周期內的不同時間段里，2臺儀器的一次項系數差異變化不大，與全樣本量總體計算的一次項系數差異的偏差均在萬分之一以內。因此，可以認為在一個觀測周期內的不同時間段可采用同一個一次項系數。

1.4 在一次觀測周期內一次項系數隨測值段的變化分析

測值段的變化包含兩部分：一是由于零漂造成的儀器自身測值段變化，二是由于空間重力變化引起的測值段變化。根據觀測經驗及已有文獻分析可知，CG-5儀器漂移較大，日變化率能達到1 000×10-8m/s2(汪健等，2016；邢樂林等，2010)，造成觀測值段一直在增大。直觀上看，一次項系數與測值段似乎存在相關性，為了研究云南測區內2臺儀器一次項系數變化與觀測值段的關系，以2018-03期觀測結果為例，在合理分配測值段及樣本量的情況下，將觀測結果大致按150 mGal的間隔拆分，分別計算每個測值段的2臺儀器一次項系數差異，結果如圖4所示。

從圖4可以看出，雖然樣本量減少，觀測誤差影響增大，但是不同觀測值段內2臺儀器的一次項系數差異總體趨勢一致，與全樣本量計算結果偏差較小，因此可以認為，在一個觀測周期內的不同觀測值段，均可采用統一的一次項系數。

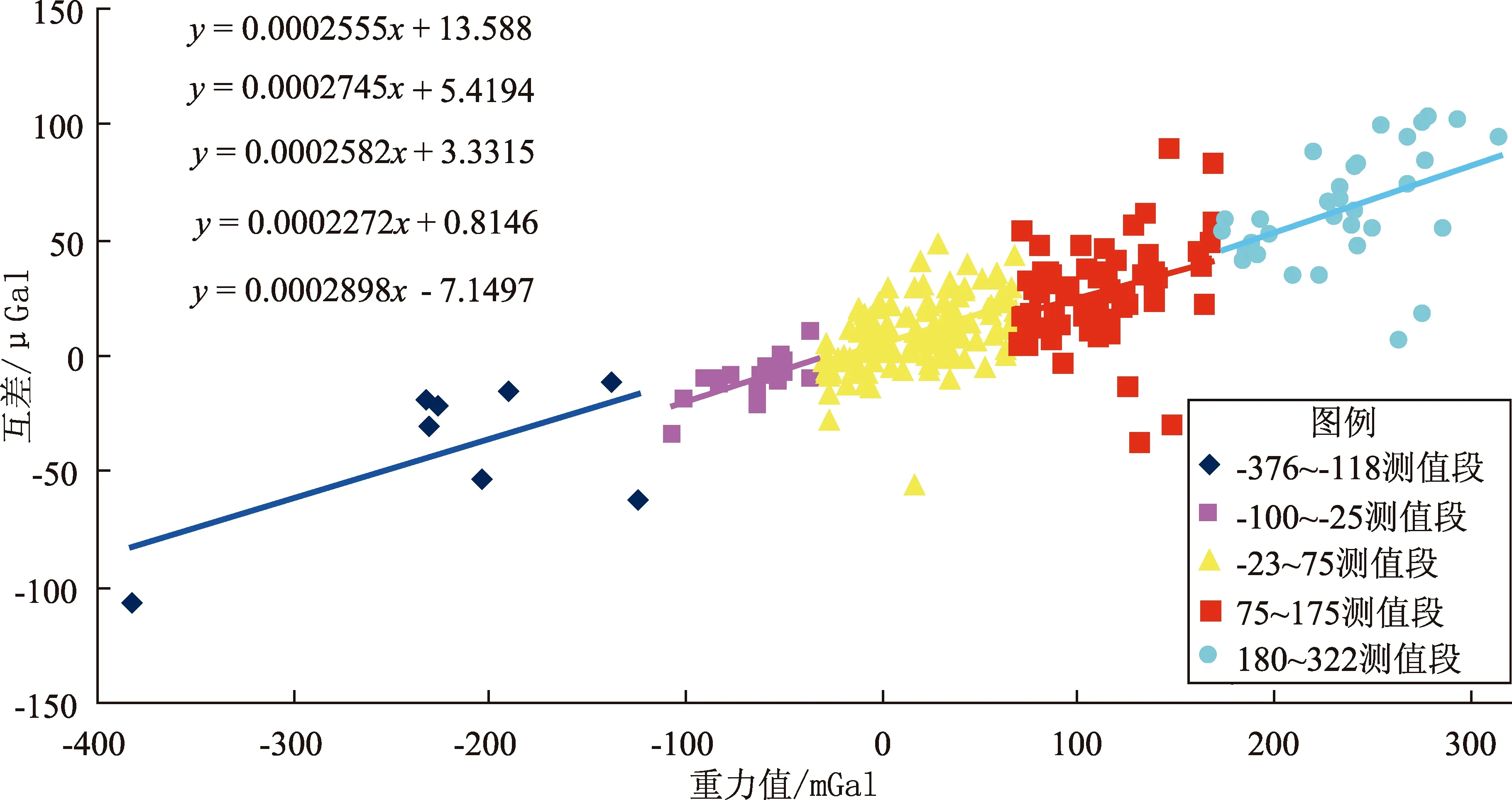
圖4 同一測量周期不同測值段內2臺儀器的一次項系數差異Fig.4 Differences of primary term coefficient of two gravimeter in different measurement periods in an observation period

1.5 各觀測周期一次項系數計算

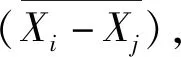
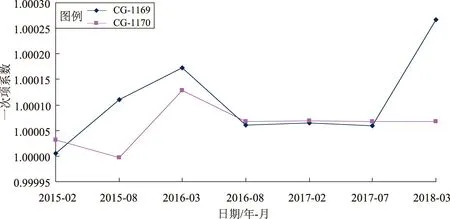
圖5 2臺儀器各觀測周期的一次項系數Fig.5 Differences of primary term coefficient of two Gravimeter in each observation period

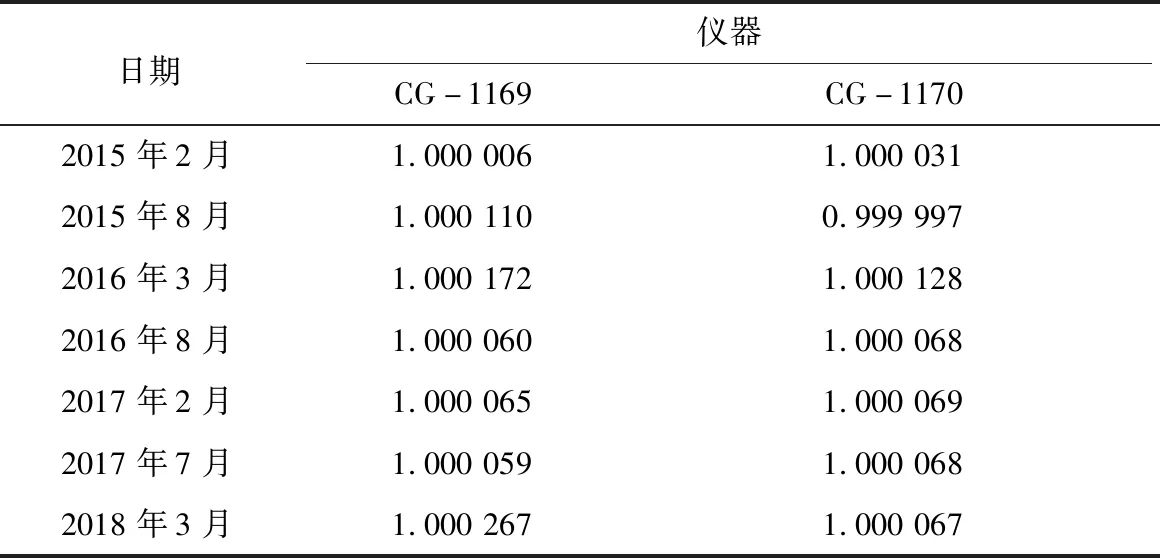
表3 各觀測周期2臺儀器的一次項系數Tab.3 Primary term coefficient of two Gravimeter in each observation period

通過圖5及表3可以看出，編號CG-1169儀器一次項系數從2015年3月至2016年8月有所變化，2016年8月至2017年7月相對穩定，2018年3月出現突變，3年內隨時間變化達到0.000 261；編號CG-1170儀器2015年3月至2016年8月有所變化，其后一直比較穩定，3年內一次項系數累計變化為0.000 036。2臺儀器3年內累計變化差異為0.000 224，與獨立分析2018-03期得出的差異基本一致，可以認為表3結果為儀器觀測時的實際一次項系數。

2 結果分析

2.1 一次項系數修正前后與絕對重力觀測值比對結果

通過上述分析發現，在一個觀測周期內，一次項系數并沒有隨著時間及觀測值段發生明顯變化，可以認為一個觀測周期內均可采用同一個一次項系數。

重力學科組在每個相對重力測區內均布設了部分絕對重力觀測點作為基準值，對相對重力觀測起到控制作用。本文以2018-03期為例，對比一次項系數修正前后相對測量結果與絕對值測量結果，對表3中的一次項系數修正結果進行驗證，驗證結果如表4所示。

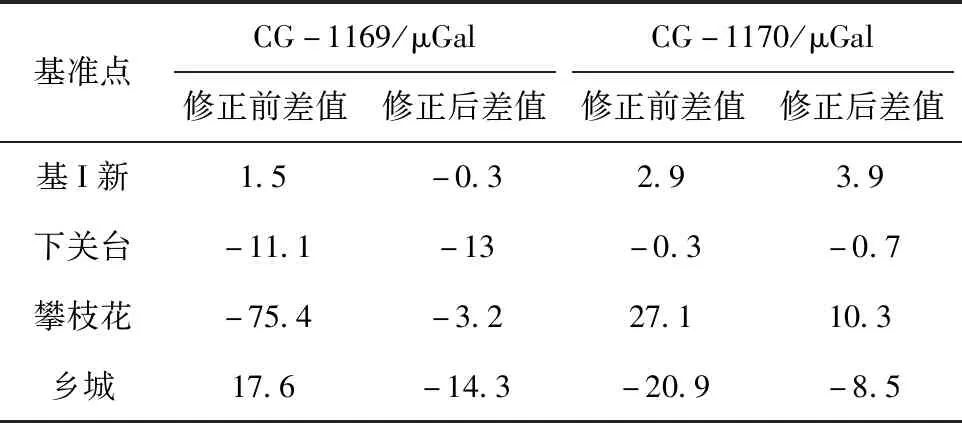
表4 一次項系數修正前后與絕對重力值的對比Tab.4 Comparison with the absolute gravity value before and after primary term coefficient correction

從表4中可以看出，一次項系數變化較大的CG-1169號儀器修正前后最大變化有72.2 μGal，并且修正后與基準值較為接近，修正效果明顯；CG-1170號儀器由于一次項系數變化不大，修正前后沒有明顯變化。綜上所述，表3中的一次項系數是合理可用的。

2.2 修正前后重力變化趨勢對比

利用修正后的一次項系數，對2015年8月至2018年3月共計6期的觀測數據進行重新計算，并繪制變化趨勢圖，本文仍然以一次項系數變化較為明顯的2018-03期觀測數據為例，對比修正前后2015-02期至2018-03期3年期重力變化趨勢情況，對比結果如圖6所示。

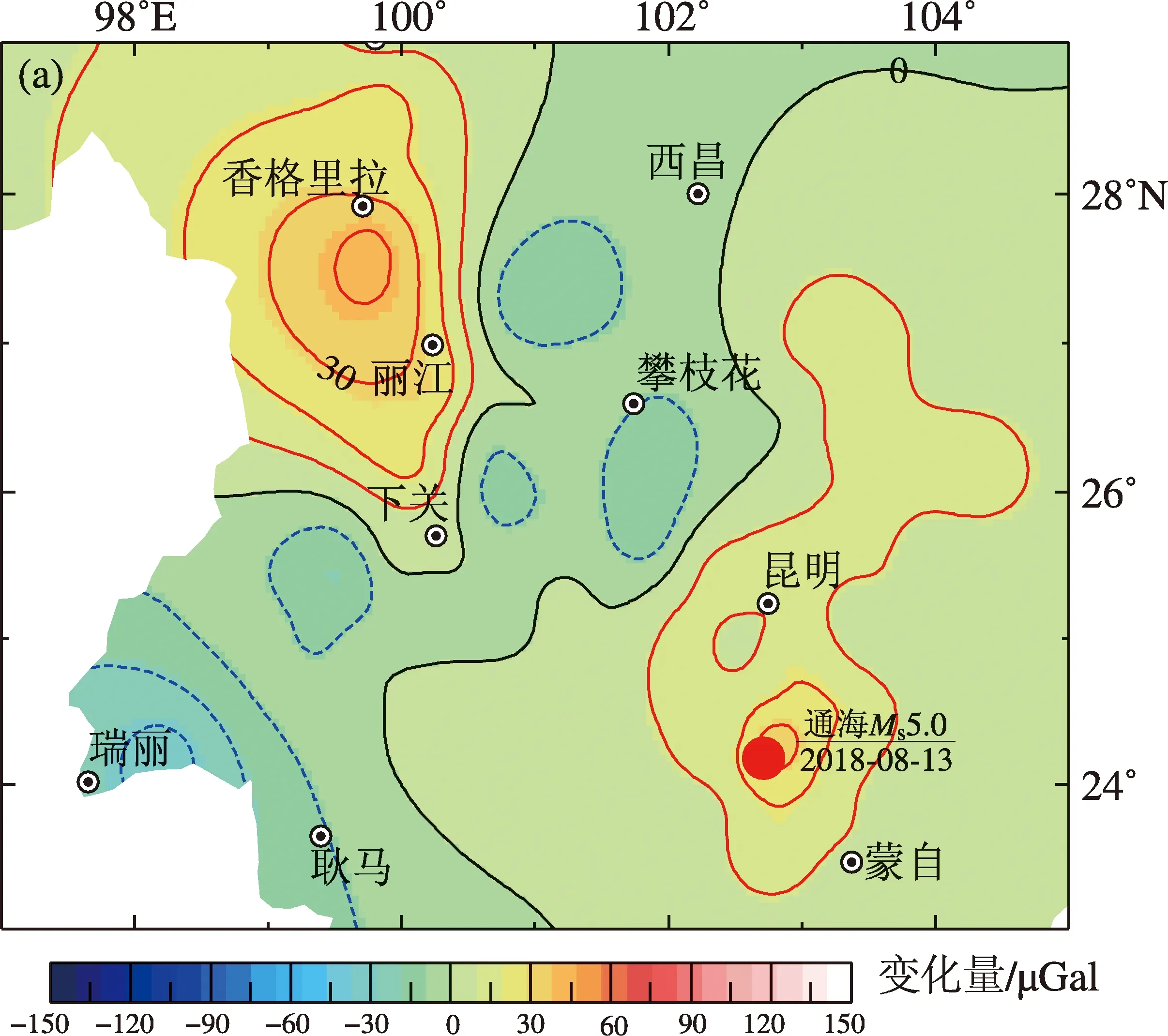
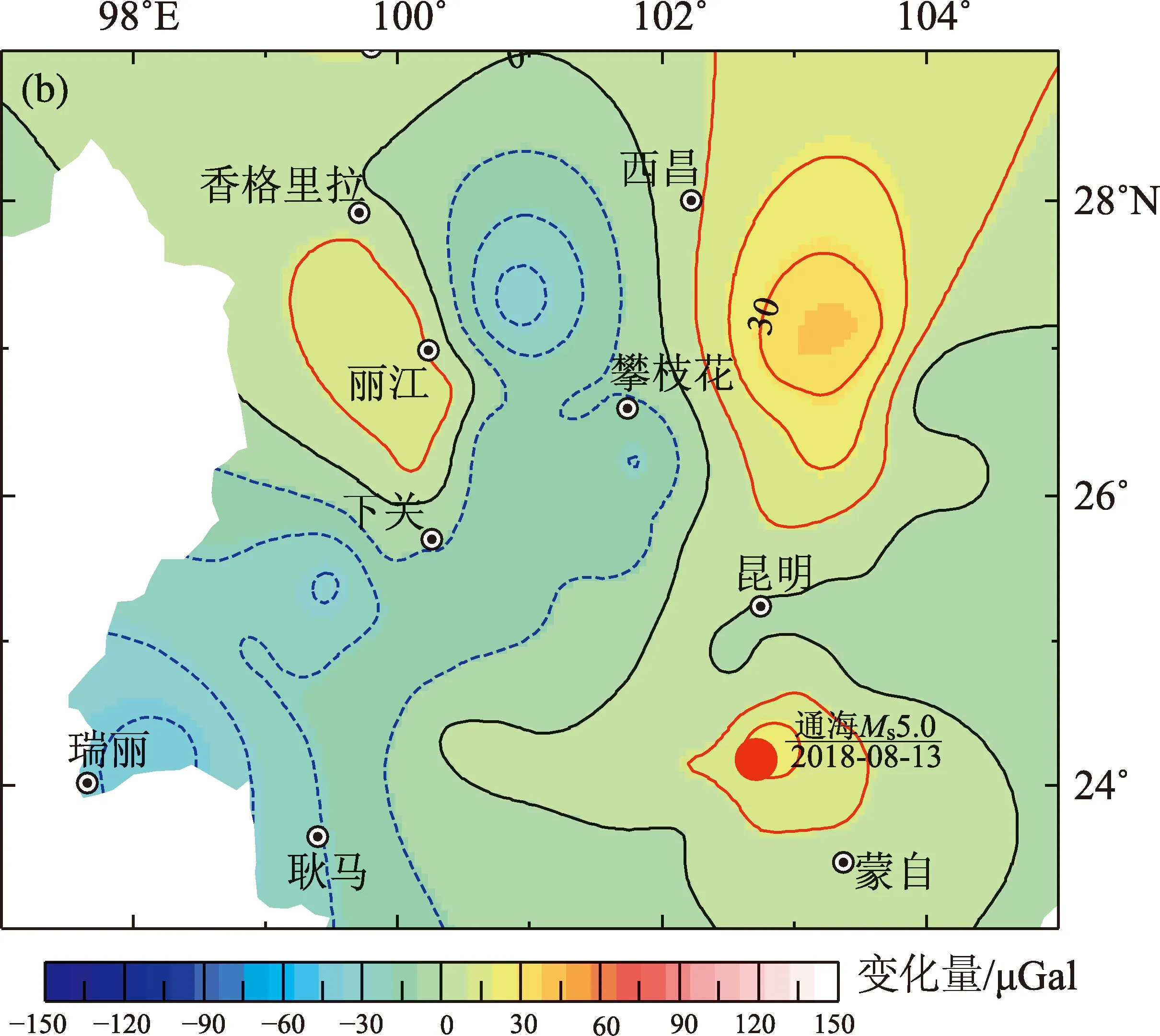
圖6 一次項系數修正前(a)、后(b)3年期重力變化趨勢圖
Fig.6 Gravity change trend map in three years before and after primary term coefficient correction

從圖6可以看出，通過一次項系數修正以后，香格里拉地區強烈的重力場增大趨勢有所減弱，但是在麗江、香格里拉、西昌至攀枝花中間形成了一個明顯的重力場減弱區域，根據以往震例經驗推斷(祝意青等，2015；張永奇等，2017)，該區域在未來中長期是具備孕育中強震的可能；通海附近的變化趨勢也更加獨立，形成了一個明顯增大的區域，與2018年下半年的通海地震相符性更強，同時可以看出魯甸地震后，其周圍區域重力恢復性增大明顯。

3 結論

通過線性回歸方法分析2015—2018年云南區域內相對重力觀測數據，結合獲取到的云南省2臺CG-5相對重力儀3年內一次項系數變化差異，利用線性回歸方法獲取3年內每個觀測周期的一次項系數，對得出的一次項系數進行驗證，分析重力變化與2018年地震相關性。得出以下結論：

(1)3年內云南測區內2臺CG-5相對重力儀一次項系數存在變化，且變化量存在差異。

(2)在一個觀測周期內，一次項系數隨觀測時間及測值段的變化會發生變化，但不明顯。

(3)通過一次項系數修正后，相對重力觀測結果與絕對重力觀測結果更為接近，說明一次項系數修正是有效可行的。

(4)通過一次項系數修正以后，測區內重力變化趨勢與地震發生的相對關系更為明顯。

利用線性回歸的方法獲取儀器一次項系數是可行的，克服了長基線標定和短基線標定在時間和空間上的限制，同時可以隨著觀測數據的增多實時進行修正，該方法在野外工作中更加適用。通過一次項系數的修正，重力觀測結果的映震效果更佳，能夠為中長期的地震預測預報提供較為有效的支持。

云南區域內的2臺CG-5型相對重力儀承擔了云南全境及貴州、四川部分區域的流動重力觀測任務，一直處于高強度工作狀態。隨著時間的推移，儀器逐漸老化，彈性疲勞明顯。在以后的觀測中，儀器在一個觀測周期內是否會隨著時間和測值段發生明顯變化，變化過程是漸進的還是會出現跳格現象，這些都需要在不斷的觀測過程中繼續分析和研究。