Majorana準粒子與超導體-半導體異質納米線*

于春霖 張浩

1) (中國長城量子實驗室, 長沙 410006)

2) (清華大學物理系, 低維量子物理國家重點實驗室, 北京 100084)

3) (北京量子信息科學研究院, 北京 100193)

Majorana準粒子是凝聚態物理版本的Majorana費米子.由于Majorana準粒子間的交換操作服從非阿貝爾統計, 并基于此可構建更穩定的量子計算機, 近年來在凝聚態物理界引起廣泛關注.為幫助初學者快速理解Majorana準粒子的形成機理, 本文回顧了在一維超導體-半導體異質納米線系統中Majorana準粒子模型的提出和理論演化過程, 介紹Kitaev鏈模型并分析了模型中各要素所起的作用.還介紹了典型Majorana器件的構成和測量方法, 并結合最新的實驗進展對探測到的零能電導峰進行了分析和述評.最后對超越一維系統的超導體-半導體異質系統的實驗前景進行了展望.

專題：拓撲物理前沿與應用

1 引 言

當今人類面臨的很多迫切問題, 例如預測全球氣候變化、開發新型藥物等, 都需要超強的計算能力來找到解決方案.隨著晶體管尺寸趨近經典物理定律極限, 傳統計算機的發展面臨巨大挑戰.在這種背景下, 量子計算作為新型計算技術的代表被寄予厚望.理論預言量子計算在一些特定的算法上會優于經典計算, 量子計算的優越性(或稱“量子霸權”)近日也被谷歌公司宣稱實現[1].然而, 可容錯的量子計算機在實際工程上面臨一個嚴峻挑戰: 量子態退相干.這是由于量子比特(量子計算的基本單元)和周圍環境不可避免的相互作用所引起的對量子疊加態或糾纏態的破壞.為了在一個量子態相干時間內進行足夠多的量子門操作, 現今主流的量子計算實現方式(比如超導量子比特)一般通過捆綁多個物理比特形成一個邏輯比特進行現場冗余糾錯來解決退相干問題.但是, 在當前物理比特的錯誤率下, 形成一個可大規模集成的邏輯比特所需的物理比特的數量可能高達成千上萬個.這給容錯量子計算機的實現設置了一個巨大的技術障礙, 目前仍然沒有實現一個邏輯量子比特.

為此, 理論物理學家在21世紀初的時候提出了利用物質的拓撲性來解決量子比特退相干的問題[2].這種思路是利用低維系統中遵循非阿貝爾統計的準粒子(或稱非阿貝爾任意子[3], non-Abelian anyon)來進行量子信息編碼.對這種任意子進行交換操作 (braiding operation, 俗稱“辮織”), 操作的結果僅與系統全局的拓撲性(也即交換的順序)相關, 從而使其免受一般局域性環境噪聲的干擾.因此, 非阿貝爾任意子被預言為可被用于實現自容錯的拓撲量子計算機[4].

非阿貝爾任意子中被研究的最廣泛的一種叫Majorana準粒子(在不同語境下又稱為Majorana零模態或Majorana束縛態), 它同時也是Majorana費米子[5]的凝聚態版本.根據理論預測, Majorana準粒子可存在于分數霍爾效應[6]、p波超導體[7]、超導-拓撲絕緣體異質體系[8]、磁性原子鏈[9]或超導-半導體異質體系[10–13]等.其中, 超導-半導體異質結構, 特別是其一維形態, 因為對材料合成要求較低且可用門電極進行調控等原因成為當前被研究最廣泛的體系之一.

在這篇綜述中, 我們將聚焦超導-半導體異質納米線體系中的Majorana準粒子.第一部分介紹Majorana準粒子的實現機理, 第二部分概述超導-半導體異質納米線體系中Majorana準粒子的實驗探測工作進展, 最后一部分展望Majorana準粒子的應用前景、技術挑戰和應對方案.

2 Majorana準粒子的實現機理

2.1 Majorana費米子

在介紹Majorana準粒子之前有必要回顧一下Majorana粒子態(即Majorana費米子)的提出過程.

在Dirac方程中, 系數 →α 和 β 的選擇需要滿足很多約束條件以及非對易關系, 1937年Ettore Majorana在考慮數學對稱性的基礎上找到了滿足該約束條件的新的一組系數以及所對應的解.用現代的方程表現形式可記為:

Majorana本人猜測中微子是一種Majorana粒子, 但至今尚未有定論.

2.2 Majorana算符

在粒子物理學里, 電子的反粒子是正電子, 而在半導體中, 可將電子的反粒子看成是空穴, 也就是說, 從系統里拿走一個電子等同于創造一個空穴.在二次量子化的表述中常用算符描述產生一個電子(或者是湮滅一個空穴), 而其共軛算符ci則描述在i態上創造一個空穴(或者是湮滅一個電子).因為電子是費米子, 需要遵循Fermi-Dirac統計, 因此和ci遵循三個很關鍵的關系[16].

在遵循以上法則的基礎上, ci和可以寫成實部和虛部分開的形式:

據此, 新定義的γi算符可以被寫成:

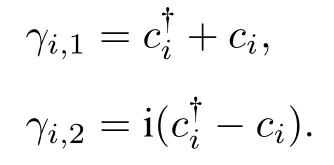
容易證明以上三條法則也適用于γi.γi是共軛對稱的:即γi是 Majorana 算符.

2.3 Kitaev-Chain模型

以上Majorana算符的推導只是一個數學游戲, 因為需要將一個電子c?空間上拆分成兩個Majorana 粒 子 (γ1和 γ2)才 有 物 理 意 義.但 是Majorana算符作為一個電子的產生和湮滅算符的疊加給了理論學家們靈感, 如果把一個電子和一個空穴疊加起來即可產生一個中性的態.例如, 超導體中的Bogoliubov準粒子便是電子和空穴的疊加態:其中 σ =↑,↓ 為自旋.可以看出, 當不考慮自旋且 u = v 時, b?=uc+uc?=b ,即得到了Majorana準粒子態.

在這種想法的指導下, Alexei Kitaev 提出了一個一維無自旋超導體鏈的玩具模型, 見圖1(后來稱為Kitaev鏈模型[18]).在Kitaev鏈模型中, 電子自旋被略去(無自旋), 其哈密頓量的離散形式可寫為

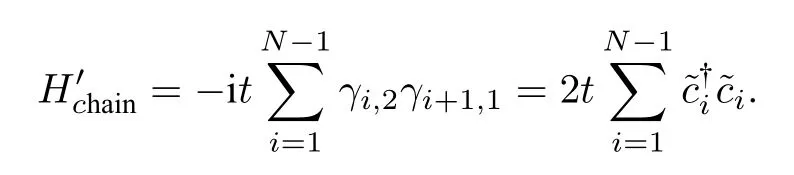
新的哈密頓量包括了除 γi, 1和 γN, 2外所有重新配對的γ算符.也就是說有一對未配對的Majorana 算符被留在了 Kitaev 鏈的兩端.γi, 1和γN, 2可以被合并為一個非局域化的費米算符沒有出現在哈密頓量里, 因此占據這個態所需要的能量為零.換句話說, 這個態被占據和未被占據兩種情況構成一個雙重簡并態,這兩個基態也就是拓撲簡并態.在理想情況下, 一個無限長Kitaev鏈兩端的Majorana態是完全無耦合的, 因此對局域噪音是免疫的.

Kitaev鏈模型的本質是在相鄰一維費米態中間提供了除電子(移動)之外的其他耦合項, 即p 波超導配對項, 使得原本的γi和γi+1?發生了位錯配對, 從而遺留了兩端未湮滅的Majorana態.

下一步便是如何在實驗室里實現電子的這種無自旋超導配對.

圖1 Kitaev 鏈模型示意圖[17]Fig.1.Schematic of Kitaevchain model[17].

2.4 Kitaev鏈的物理實現

無自旋臨近電子配對模型在實際情況下對應的是自旋極化配對(也被稱為自旋三重態配對), 因為這種超導模型的對稱性與原子模型中的p軌道類似, 因此又常稱為p波超導體(常見的BCS超導體則對應s波超導體).本征的p波超導體在自然界中很罕見, 有些超導體被認為有可能是自旋三重態配對超導體, 例如Sr2RuO4, 但目前仍處于爭論中[19].

為了得到p波超導配對, Fu和Kane[8]設想把傳統的s波超導體和拓撲絕緣體耦合成一個異質體系后, 超導的臨近效應會使得拓撲絕緣體表面的自旋鎖定態出現p波配對的超導表面態, 而Majorana準粒子態就會出現在超導表面態的邊緣、端點或漩渦處.受此啟發, Sau等[10]又證明了可以把上述人工結構中的拓撲絕緣體替換為實驗室中更加常見的半導體而使得Majorana異質系統的實現更加容易.他們預言的新系統為一個三明治系統: 一層具有強自旋軌道耦合 (spin-orbit interaction, SOI)的半導體量子阱材料夾在一層鐵磁絕緣體和一層超導體中間.隨后, Alicea[11]又發現其實相對罕見的鐵磁絕緣體也不是必須的, 可以用一個垂直于SOI場的外部磁場進行替代.緊接著, Lutchyn等[12]和Oreg等[13]又證明了具有強SOI的一維納米線也可以實現一維版本的Majorana系統, 該系統數學上和Kiteav鏈模型等價.

因此, 利用具有強SOI的半導體納米線[例如砷化銦(InAs)[20]或者銻化銦(InSb)[21], 并將其與常見的s波超導體[例如鈮(Nb)或者鋁(Al)]進行耦合, 在外加磁場的幫助下, 納米線兩端便可出現Majorana準粒子態(圖2).為了清晰地分析在此模型中SOI、超導體能隙?和外加磁場B對Majorana準粒子產生的影響, 我們建立了數值模型對每個參數進行獨立分析.為此, 異質納米線的哈密頓量可以寫為

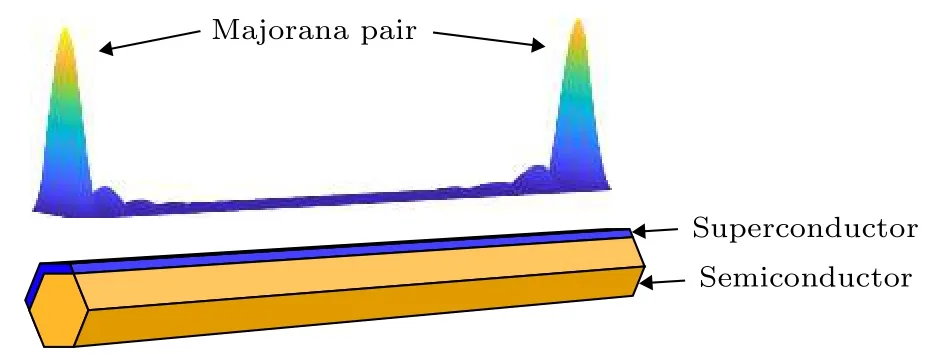
圖2 一維超導體-半導體異質結構與 Majorana 準粒子態波函數示意圖Fig.2.Schematic sketch of a nanowire-superconductor hybrid structure and the wave function of the Majorana quasiparticle.

圖3 超導體-半導體異質納米線體系在不同的?-Ez-α 配置下的能量色散圖譜 (μ = 0).其中, 藍線和紅線分別對應兩個自旋分支(SOI方向投影), 實線對應粒子項分支, 虛線對應空穴項分支Fig.3.Energy dispersion of a superconductor-semiconductor hybrid nanowire at different ?-Ez-α configurations with μ = 0.Blue and red lines correspond to the two spin branch (along SOI direction), respectively, solid lines are particle branches, while dashed line are hole branches.

3 超導-半導體體系Majorana零模態的實驗進展

在以上理論研究指導下, 實驗上在超導體-半導體納米線復合系統中尋找Majorana準粒子迅速成為過去十年凝聚態物理研究的一個熱點方向.其實在Majorana準粒子相關理論提出之前, 針對強SOI半導體納米線就已經有了很多實驗研究.例如, 對InAs和InSb納米線的電子輸運測量表明它們是強 SOI、高 g-因子、高遷移率材料[20–23], 且可與超導體形成較好的耦合[24,25]等.

2012年荷蘭Delft理工大學團隊報道了在高轉變磁場超導材料NbTiN與InSb納米線的耦合系統圖4(a)中觀察到的零能電導峰信號作為Majorana存在的可能證據[26], 且發現該零能電導峰與三維磁場的指向有關.不久, Lund大學和Weizimann研究所分別利用InSb-Nb[27]和InAs-Al[28]等結構觀察到類似的零能電導峰.

這些零能電導峰實驗用到的典型器件結構是由普通金屬(如鈦/金等)作為探測端與半導體納米線連接, 被探測端則是將超導體覆蓋到半導體上形成異質結構.探測端與被探測端有一小段裸露的半導體納米線, 可通過門電極控制其勢壘高度從而形成隧穿結.超導體-半導體異質結構部分也有相應的門電極用于調控其電化學勢.對這樣的器件再施加一個與SOI垂直的磁場, 磁場足夠強時即可誘發拓撲相變從而形成Majorana準粒子態.

圖4 超導體-半導體異質器件與探測到的零能電導峰 (a)?(c) NbTiN-InSb 器件與零能電導峰[26]; (d)?(f) 全外延 Al-InAs納米線及純凈超導能隙中的零能電導峰[29]; (g), (h)全外延Al-InSb納米線器件中量子化的零能電導峰[40]Fig.4.Superconductor-semiconductor hybrid devices and the detected zero-energy conductance peaks: (a)?(c) NbTiN-InSb nanowire device and zero-energy conductance peak[26]; (d)?(f) Fully epitaxial Al-InAs nanowire and zero-energy conductance peak in hard gap[29]; (g), (h) Quantized zero-energy conductance peak in fully epitaxial Al-InSb nanowire devices[40].

比較理論所預測Majorana零能電導峰[30,31]和實驗探測的零能電導峰會發現有兩個顯著的不同點.一是理論預測的Majorana引起的零能電導峰是處在超導體所形成的能隙中, 而實驗所得的零能信號則是伴隨很多雜態;二是由于Majorana準粒子態引起的安德烈夫反射過程具有完美的粒子-空穴對稱性, 其引發的電導峰應該是一個值為2e2/h的量子電導, 而實驗中觀察到零能電導峰并未出現量子化行為.為了解決這些理論與實驗的不一致性, 實驗上對材料和器件的制備工藝的優化成為該方向發展的瓶頸和突破口.

首先, 與零能電導峰伴隨的其他雜態一般被認為是由于器件中存在大量缺陷所致.這其中很大一部分原因要歸結于超導體與半導體界面的不平整.在實驗器件制備過程中, 為了使超導體與半導體形成均勻的電接觸, 需要移除納米線外面的氧化層.這個過程最先是通過氬離子轟擊刻蝕的方式進行,但同時會對納米線表面造成損傷而產生大量雜質.后來通過化學溶液有選擇性地腐蝕掉氧化層并進行鈍化[32], 器件的界面質量得到了顯著提高, 并在輸運上表現出彈道輸運的量子化電導平臺[33,34], 但能隙內部的雜態數量(特別是在高磁場情況下)仍然較多[35].

器件質量更大的突破來自于分子束外延(MBE)超導體-半導體生長技術日趨成熟所帶來的原子級平整的界面[36], 從而直接導致無雜質態的近鄰超導能隙[37].利用MBE外延Al-InAs材料, 純凈能隙中的零能電導峰很快也被探測到, 實驗信號的干凈程度比上一代實驗有了顯著提高[38].全外延技術很快也被成功應用到Al-InSb系統的生長上[39].由于InSb本身的彈道輸運特性和更小的系統耗散, 配合以遮擋法形成的天然隧穿結, Majorana理論所預言的量子化的零能電導峰在實驗中也很快被探測到[40].

自第一代實驗以來, 零能電導峰雖然符合Majorana理論預言, 但同時也有很多其他可能的平庸解釋.隨著材料和器件質量的不停優化以及理論模型的完善[41–46], 每當在更干凈的器件中觀察到信號質量更好的零能電導峰, 一部分平庸的解釋就會被排除掉, 人們對納米線體系中Majorana存在的信心就會進一步增加.迄今為止, 當初大部分的平庸解釋已被排除, 但在極少數的條件下仍然有可能有平庸的解釋.因此零能電導峰并不能成為Majorana準粒子態存在的最終證據, 特別是有一些平庸Andreev束縛態在特定形狀的勢阱中仍有可能出現類似Majorana束縛態的信號[47–54].該勢阱通常要求電化學勢在空間緩慢變化, 故寬度更窄(高度更高)的隧穿結可能成為下一步努力方向[55].最終能充分證明Majorana準粒子態及其拓撲特性的實驗只有通過辮織操作來驗證其非阿貝爾統計性[18,56].

除零能電導峰外, 另一個探測Majorana零模的輸運手段是引入電子的充電能(charging energy).將超導-半導體納米線做成島狀器件結構時, 庫侖相互作用導致電子只能逐個通過該島.而當超導能隙大于充電能時, 電子能以庫珀對的形式兩兩通過該島, 輸運上表現為兩電子周期的庫侖阻塞峰.在此基礎上加磁場后在島的兩端產生兩個Majorana零模時, 電子可以以‘隱形傳態’的方式從島一端的Majorana零模進去, 然后從另一端的Majorana零模隧穿出來[57], 輸運表現為單電子的庫侖阻塞峰.這種從雙電子到單電子的庫侖阻塞峰的演變在解決了納米線器件中雜質(hard gap)問題后也在實驗上被觀察到[58?60].不過該實驗手段也面臨著和隧穿實驗類似的問題: 如何排除其他的平庸解釋(比如Andreev束縛態)[54,61,62].

該方向過去數年理論的進展大致可分為三個方面: 1)提出其他可能的平庸解釋, 主要是細致研究Andreev束縛態和Majorana零模之間的相似與不同[46?48,50?53].2)建立更精確的納米線實驗器件的理論模型.理論模型從簡單的一維擴展到三維(多個子能帶)[31]; 研究無序(電化學勢、自旋軌道耦合、超導配對等)帶來的變化[48,50,63]; 用Schr?dinger-Poisson等自洽的方法研究納米線器件中的門電極、超導半導體耦合等效應[42,43].3)提出新的Majorana探測和辮織方案.第一代辮織方案要求用門電極實現對Majorana零模在空間上的快速移動[56].這一方案因超導的屏蔽效應而在實驗上非常具有挑戰性.后來隨著理論發展, 不需要移動Majorana零模, 只利用充電能和單電子在兩個Majorana之間的隱形傳態就可實現在數學上等價的辮織操作[64,65].這種基于測量的辮織方案(measurement-based braiding)是當前實驗努力的主流方向[66?68].而基于此, 實驗上也實現了各種復雜的納米線網格結構[39,69], 最近的突破是源自于選區外延生長技術的發展[70?72].

4 展 望

除了非阿貝爾辮織操作這一長遠目標, 短期內利用超導-半導體納米線還可以做很多相對容易的實驗以揭示Majorana物理的不同方面[73].例如,用來檢驗Majorana非局域特性的雙端電導對照實驗[74], Majorana-量子點耦合實驗[75]等.另外, 比一維納米線更加復雜的納米線交叉結構[69]、納米線網格結構[70]和二維拓撲材料體系[76]也被成功合成出來, 并展現出廣闊的應用前景.特別地, 多維體系對實現Majorana辮織操作[56]和最終的拓撲量子計算有著至關重要的意義.毫無疑問, 接連不斷的技術挑戰和嶄新的物理發現在未來Majorana器件研究中是并存的, Majorana準粒子的研究才剛剛開始.