束勻滑光束偏折現象的模擬*

李斌 劉占軍 郝亮 鄭春陽 蔡洪波 何民卿

(北京應用物理與計算數學研究所, 北京 100094)

達到高能量密度物理狀態后, 光束在介質中的傳播行為與經典光學研究范疇相比, 會出現一些新現象.比如在各向同性介質內可出現光束傳播方向改變的現象.另一方面, 高能量密度物理實驗中由高功率激光器產生的束勻滑光束較為常見.本文分析了空間和時間束勻滑光束在各向同性等離子體傳播中出現束偏折現象的機制和條件, 并利用三維激光等離子體相互作用程序LAP3D進行了驗證.模擬表明只有當同時發生成絲不穩定性和存在離子聲速量級的橫向流時束勻滑激光才會產生顯著的束偏折現象.

1 引 言

在經典光學范圍內, 光束在各向同性介質內的傳播方向不會發生改變, 傳播方向改變的現象通常發生在不同介質的交界面處.但當能量驅動源如激光, 使介質能量增加并達到高能量密度狀態后, 激光強度足以改變介質折射率, 在這種介質內也會發生光束傳播方向改變的現象(束偏折)[1].另一方面在高能量密度物理研究中, 隨著近年來高功率激光器技術的發展, 采用激光束輻照產生高能量密度狀態成為一種常用的方式.許多采用大型高功率激光器的實驗, 通常輸出束勻滑光束[2?8].針對高能量密度狀態下, 束勻滑光束發生束偏折的機制和條件, 本文給出了相關研究結果.

束勻滑光束按光束勻滑方式可分為空間束勻滑和時間束勻滑兩種.它們的共同特點是光束包絡較為平滑, 但內部結構較為復雜, 內部包含數千個小光斑, 縱向長度為 8 F2λ0[1,2], 橫向長度為 2 Fλ0[1,2],這里F為透鏡光學F數, λ0為激光波長.分析束勻滑光束發生束偏折的條件, 要從光束內部多個小光束相互作用角度考慮, 涉及到多體相互作用, 僅應用理論分析較為困難.如果不考慮光束內部結構, 僅從整個光束角度考慮, 其發生束偏折的條件在一定程度上可類比單個光束, 如高斯型光束發生束偏折的機制和條件, 本文從這個角度展開了對束勻滑光束發生偏折現象所需條件的分析和研究.

實驗研究[9,10]和近期利用LAP3D程序對高斯型光束的模擬研究[11]都表明, 高斯型激光束發生顯著偏折需滿足兩個條件: 發生成絲不穩定性和存在聲速量級的等離子體橫向流[11].前者在聚焦光斑處形成密度凹坑并改變此區域折射率, 后者使這種密度空間結構能在橫向整體移動.據此認為研究束勻滑光束發生束偏折的條件可進一步細化為研究以下兩點: 束勻滑光束發生成絲不穩定性的條件以及聲速量級的等離子體橫向流對成絲不穩定性的影響.

本文根據以上兩個條件對束勻滑光束偏折現象的產生機制和條件進行了研究, 給出了用于模擬三維束勻滑光束偏折現象的數值模擬程序LAP3D的物理建模, 分析了橫向流大小對不穩定性發展的影響, 給出了研究空間束勻滑光束和時間束勻滑光束發生束偏折條件的數值模擬結果和分析.

2 物理模型

2.1 光束傳播模型

為描述光束在等離子體中的傳輸和等離子體響應, 三維激光等離子體相互作用程序LAP3D分別采用了激光包絡方程和雙溫流體方程組[12,13]的物理模型.由于束偏折現象發生與否跟光束成絲現象緊密相關, 因此在激光傳播模型中只考慮衍射項和折射項, 忽略激光受激散射項, 對應的包絡化激光傳播方程為

其中, E 為激光電場強度; vg為激光波包傳播群速度; c 為真空中激光光速; ω0為激光頻率; ν 為逆軔致吸收率; me為電子質量; δ nef為電子擾動數密度;為廣義衍射算子[12], 在下文推導中為簡化用來代替.

2.2 流速對束偏折(成絲)發展影響的分析

設沿激光傳播方向為z方向, 存在橫向(沿x方向)流速為 u⊥的等離子體流場, 考慮流體方程組中的質量連續方程:

和動量方程:

其中, S 為電子動量, u 為流速, Q 為人為粘性應力張量, ψ 為有質動力勢, p 和 pe為離子壓力和電子壓力.

對上面兩個方程線性化, 設 E =E0+δE ,n=n0+δnef, 則質量連續方程和動量方程經化簡后, 可得 δ nef滿足的密度漲落方程為

其中, cs為離子聲速, M 為離子質量, 對 (1)式和(4)式做傅里葉分析可得色散關系為

A-A′剖面(圖2)顯示，F3斷層在熱水塘村一帶上覆有良好的保溫蓋層，熱儲層中的熱液沿該斷裂上升出流，在地表形成溫泉，其中S18溫泉溫度45 ℃，水量較大。C-C′剖面(圖3)直觀地反應出該區燈影組地層是良好的熱儲層，但因蓋層較薄，鉆孔抽水人為加劇地下水循環，進而導致降雨入滲混入熱儲層造成論證區熱儲層溫度不會太高。

考慮 ω =iγ ? ω0并且 k ·k0=0 , 化簡得到光束傳播過程中存在橫向小擾動及有橫向流場發生成絲不穩定性對應的空間增長率:

式中, γ 為成絲增長率, k⊥為橫向擾動波數, k0為入射光束波數, vos和 ve分別為電子在光場中的抖動速度和熱速度.

對于在各向同性等離子體中傳播的高斯光束,可認為在給定參數下 (6)式中物理量 ve、 vos、 ne、ncr、 k0、 cs均為定值.在光束的擾動波數 k⊥范圍內,以 kopt為例考察(6)式中橫向流大小對不穩定性發展的影響.這里 kopt為沒有橫向流時, 在此條件下使成絲不穩定性增長率取最大值時對應的擾動波數.進一步分析(6)式可知, 當橫向流速為離子聲速時, 對應不穩定增長率為極大值; 當流速逐漸小于離子聲速時, 不穩定性增長率逐漸減小, 發生成絲的空間位置也逐漸“靠后”; 當流速大于離子聲速時, 成絲發展受抑制.

結合本節第一段所描述的模擬結果[11], 上面分析表明, 對高斯型光束, 橫向流對其束偏折的影響本質上是橫向流對成絲不穩定性發展的影響.考慮到束勻滑光束包絡內部包含多個小焦斑, 其光強分布可近似等同于高斯光束, 因此可推斷束勻滑光束發生顯著的束偏折現象也需滿足發生成絲不穩定性和存在聲速量級橫向流的條件.本文下面兩節將采用數值模擬研究的方法來進一步分析和判斷.

3 空間束勻滑入射光束數值建模和束偏折模擬結果

激光器產生的入射光束通過位于聚焦透鏡前的相位板后, 被分割成多個子光束, 在遠場疊加形成空間束勻滑光束.本文模擬中應用連續相位板(continuous phase plate, CPP), 它使子光束間相位差在 0到 π 之間連續變化, 對比隨機相位板, 不僅在遠場可產生更為平滑的包絡分布, 也使焦斑中能量提高到入射光能量的95%[14].

焦平面內經CPP后生成的空間束勻滑光束的電場幅值分布可表示為下式:

其 中, f為 透 鏡 焦 距 , E (x,y) 為 入 射 光 復 振 幅,t(x,y)為CPP的相位信息.

LAP3D程序采用笛卡爾坐標系, 模擬三維大尺度上發生的空間束勻滑光束偏折現象.模擬中激光從 (x, y) 面入射, 沿 z 方向傳播.(x, y, z) 方向上對應的模擬尺度分別為 ( 2048λ0,2048λ0,2048λ0) ,單位為激光波長 λ0, λ0= 0.351 μm.模擬空間內等離子體均勻分布, 初始等離子體密度為 0.1nc, 電子溫度 Te為 3 keV , 離子溫度 Ti為 1 keV , 離子電離度 Z =1.

模擬中采用光學 F數為 11, 長軸約為200 μm, 短軸約為 100 μm 的橢圓焦斑 F200, 橢圓焦斑內的電場幅值分布如文獻[15]中圖1所示.根據空間束勻滑光束入射面平均光強大小, 設計了5個模型.首先模擬了在沒有橫向等離子體流的條件下, 空間束勻滑光束在均勻等離子體中的傳播行為, 重點考察是否發生了光束成絲現象.然后引入聲速量級的橫向流, 再次計算上述5個模型, 重點考察是否發生了光束偏折現象.等離子體橫向流由x方向左邊界流入, 從x方向右邊界流出, 垂直于激光傳播方向.這些模擬結果如表1所示.

對于空間束勻滑激光在均勻等離子體傳播過程中能否發生成絲現象, 可根據下面公式[15]來判斷,

其中, Iav, λ0, ne, nc, Te和 F 分別為光斑平均光強、激光波長、電子密度、等離子體臨界密度、電子溫度和光學F數.當空間束勻滑入射光束平均光強大于 Iav時, 空間束勻滑光束在傳播過程中會發生成絲現象; 反之, 小于此值時, 空間束勻滑光束不成絲.根據上文給出的模擬參數, 可知表1中模型 3, 4, 5 可發生成絲不穩定性情況, LAP3D 模擬結果也證實了這一點.

表1 空間束勻滑光束F200成絲和束偏折現象模擬結果Table 1.Simulation results for filamentaion and beam deflection in the case of CPP smoothed beam F200.

圖1 不同激光強度下空間束勻滑光束對應的束偏折模擬結果 (a) F200模型2加橫向流; (b) F200模型5加橫向流.圖中橫縱坐標對應模擬空間坐標z和x, 其量綱為激光波長.橫向流速等于離子聲速Fig.1.Beam deflection simulation results at different incident intensity: (a) Transverse flow and average intensity lower than filamentation threshold; (b) transverse flow and average intensity higher than filamentation threshold.x and yaxes of two figures corresponding to xand z axes of simulation coordinates, respectively.The spatial scale is in unit of laser wave length.The transverse flow speed equals ion sound speed.

圖2 對比空間束勻滑光束發生束偏折時F200模型5加橫向流的入射面和出射面內光斑電場幅值分布 (a)入射面; (b)出射面.圖中橫縱坐標對應模擬空間坐標x和y, 其量綱為激光波長.橫向流速等于離子聲速Fig.2.Comparison of spatial distribution of laser electric field between laser entrance and exit planes as beam deflection presents:(a) Laser entrance plane; (b) laser exit plane.x and y axes of two figures corresponding to x and y axes of simulation coordinates,respectively.The spatial scale is in unit of laser wave length.The transverse flow speed equals ion sound speed.

對于束偏折現象的模擬表明, 如果空間束勻滑光束發生了成絲現象, 則引入聲速量級的橫向流后, 光束會發生顯著的束偏折現象; 反之, 如果光束沒有發生成絲現象, 則不會出現束偏折現象.如圖1所示, 模型2中沒有發生激光成絲現象, 加橫向流時對應的模擬結果中光束傳播方向沒有變化;而模型5中發生了激光成絲現象, 加橫向流后對應模擬結果顯示光束傳播方向隨傳播距離增加明顯偏向等離子體流方向, 即發生了束偏折現象, 這些模擬結果與物理預期相同.

此外從空間束勻滑光束入射面和出射面內光斑電場幅值空間分布情況也可判斷光束是否發生了明顯的束偏折現象.如圖2所示, 對比F200模型5加橫向流時模擬結果給出的電場幅值在入射面和出射面內的分布, 可以發現在出射面內光斑整體偏向等離子體流的方向, 表明發生了束偏折現象.

F200對應的模擬結果表明, 影響空間束勻滑光束明顯發生束偏折的物理條件與高斯光束時的主要物理因素相一致, 即空間束勻滑光束滿足成絲條件和存在流速在離子聲速量級的等離子體橫向流.

4 時間束勻滑入射光束數值建模和束偏折模擬結果概述

采用時間束勻滑的典型應用為譜色散勻滑化技術, 它利用光柵、三倍頻晶體, 展寬入射光束頻率, 然后使光束通過相位板和聚焦透鏡, 形成遠場的譜色散勻滑 (smoothing by spectral dispersion,SSD)光束, 其傳播主要特征表現為光束在橫向上的“掃描”行為[16].SSD光束在焦平面上的光強分布為

式 中, 3δ 為 調 制 振 幅; ?m為 調 制 頻 率; (p,q)=(x,y)k?/(2f), x ,y 為焦平面上的空間坐標, k 是三倍頻后的波數, ? 為相鄰相位板面元之間的距離;?KL為 ( K,L) 通過相位板面元造成的相移;γ=α?/2, 是由不同頻率以不同角度入射造成的位移.修改(9)式可得LAP3D程序中采用的入射面上光強分布的數值計算模型為[16]

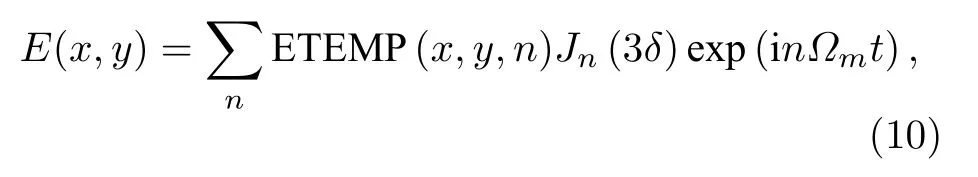
其中

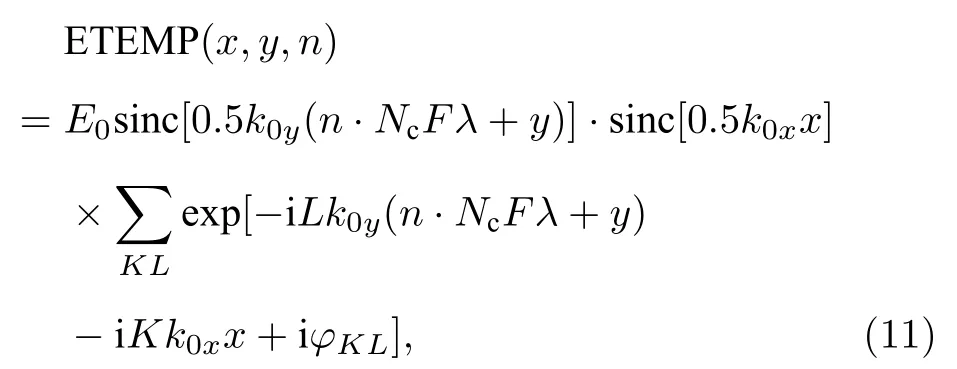
仿照上節研究空間束勻滑光束出現束偏折現象條件的思路, 可認為對于SSD勻滑光束, 發生束偏折的前提是發生成絲不穩定性.因此這里首先考察SSD光束發生成絲的條件.美國學者Kruer等[17?21]研究分析了有一定帶寬的激光抑制不穩定性發展的條件, 指出當不穩定性增長率為 γ0的波引入帶寬?ω時, 不穩定性引發的振幅增長可被削弱為沒有帶寬時的 γ0/?ω 倍, 即

為考察SSD帶寬對其在等離子體傳播過程中發生束偏折的影響, 用LAP3D模擬了三種不同調制頻率的SSD光束在均勻等離子體中的傳播, 這里取調制頻率分別為 1 0?3ω0, 1 0?4ω0和 1 0?5ω0.模擬中取入射SSD光束光斑平均光強為2.11×1015W/cm2, 其余模擬參數與上節中算例相同.

根據模擬參數, 可分析哪種調制頻率會出現束偏折現象.成絲不穩定性最大增長率 γmax為

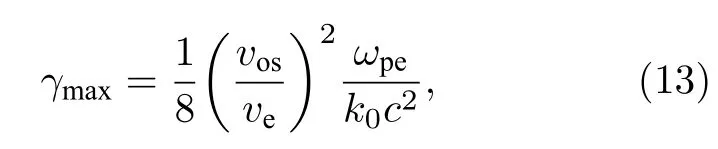
其中, vos, ve, ωpe, k0, c 分別為電子在光場中的抖動速度、電子熱速度、等離子體頻率、光束波矢和真空光速.根據上文模擬參數可知成絲不穩定性最大增長率 γmax≈ 2.56×10?4ω0.SSD光束帶寬?ω為

其中, δ 為調制深度, 模擬中取 δ =12 , fSSD為調制頻率.由本文算例所取的SSD光束調制頻率可知,當 SSD 光束調制頻率 f SSD 為 1 0?3ω0和 1 0?4ω0時,SSD光束帶寬均遠大于算例對應的成絲最大增長率 γmax≈ 2.56× 10?4ω0.但當SSD光束調制頻率fSSD為 1 0?5ω0時, SSD光束帶寬小于成絲最大增長率.

根據上面的理論分析, 可以預期在取10?3ω0和 1 0?4ω0這兩種調制頻率時, 時間束勻滑光束可以抑制成絲不穩定性; 相應束偏折現象也不會出現.當 SSD 光束調制頻率為 1 0?5ω0時, 可發生成絲不穩定性; 當同時存在聲速量級橫向流時會出現顯著的束偏折現象.下面給出的模擬結果也證實了這些判斷.

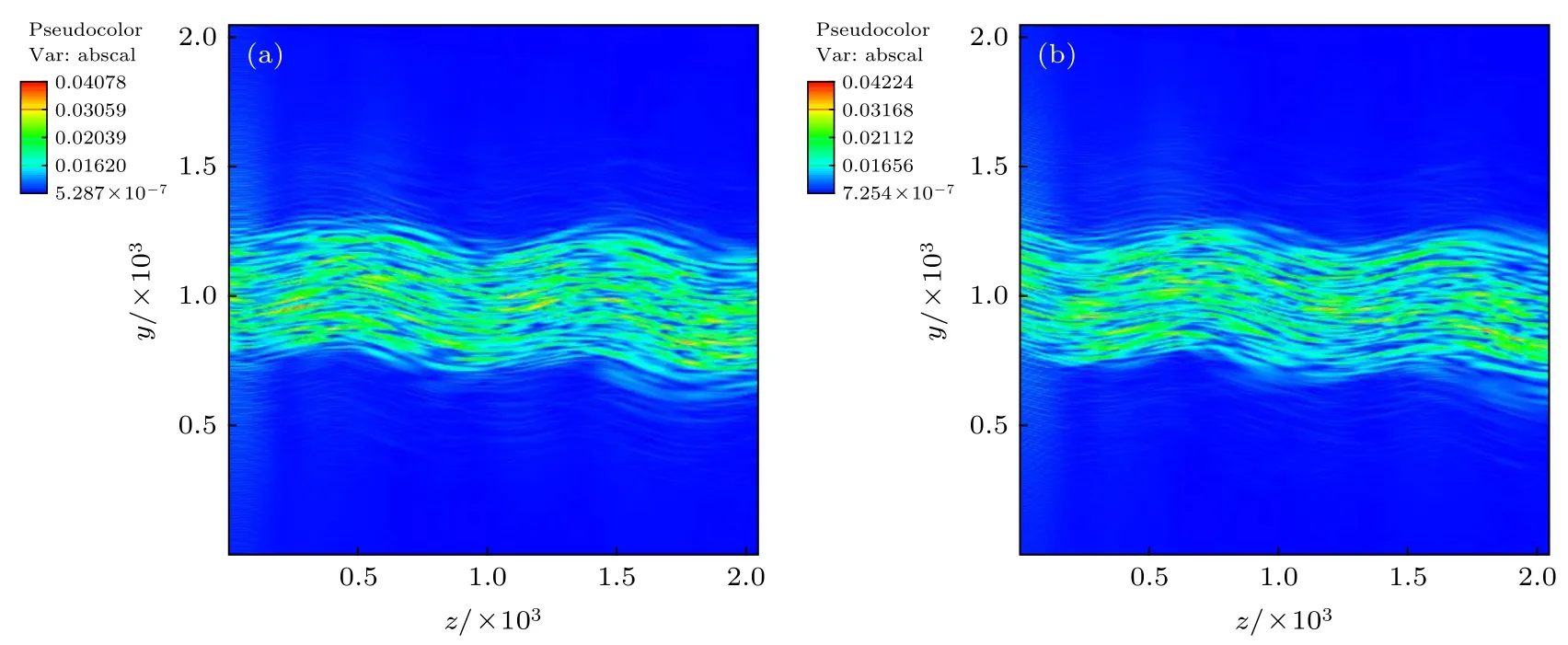
圖3 調制頻率為 1 0?3ω0 的時間束勻滑光束傳播行為 (a)對應11000激光周期; (b)對應13750激光周期.圖中橫縱坐標對應模擬空間坐標z和y, 其量綱為激光波長Fig.3.Propagation of SSD beam at modulation frequency of 10–3w0: (a) Corresponding simulation result at 11000 th laser periods;(b) corresponding simulation result at 13750 th laser periods.x and y axes of two figures corresponding to z and y axes of simulation coordinates, respectively.The spatial scale is in unit of laser wave length.

圖3給出了當SSD光束調制頻率為 1 0?3ω0且沒有橫向流時的傳播過程的模擬結果.模擬發現,在給定的傳播距離內(約2000個激光波長), 與空間束勻滑光束成直線傳播相比, SSD光束在空間傳播中表現出明顯的“掃描”行為, 這和已有模擬結果[16]和理論預期相符.

由上一節給出的模擬結果可知在給定的等離子體條件下, 本節算例中的SSD光束強度遠大于成絲閾值, 但圖3中顯示SSD光束并沒有出現束發散現象.這表明當SSD光束取調制頻率為10?3ω0時, 抑制了成絲不穩定性.由此可以預期,當加入等離子體橫向流時, 也不會明顯發生束偏折現象, 模擬結果證實了這一點(圖4).

除調制頻率為 1 0?3ω0的情況, 還模擬了SSD光束調制頻率為 1 0?4ω0時, 無橫向流和有橫向流時的激光傳播情況.模擬結果表明, 無橫向流時算例沒有出現激光成絲現象, 相應模擬流速在離子聲速量級的橫向流時的算例如圖5所示, 也沒有出現束偏折現象.當調制頻率為 1 0?5ω0時, 模擬結果表明: 無橫向流時, SSD 光束會出現成絲現象; 有橫向流時, 光束會出現束偏折現象.由于其調制頻率較低, 所以在本文所選的模擬空間尺度內, SSD光束傳播行為類似于前一節的空間束勻滑激光, 如束發散時光場空間分布的模擬結果與圖1(b)類似,故這里略去.

圖4 有橫向離子聲速量級等離子體流時調制頻率為 1 0?3ω0 的時間束勻滑光束的傳播行為 (a)對應11000激光周期; (b)對應13750激光周期.圖中橫縱坐標對應模擬空間坐標z和y, 其量綱為激光波長.橫向流速等于離子聲速Fig.4.Propagation of SSD beam with transverse flow at modulation frequency of 10–3 w0: (a) Corresponding simulation result at 11000 th laser periods; (b) corresponding simulation result at 13750th laser periods.x and y axes of two figures corresponding to z and y axes of simulation coordinates, respectively.The spatial scale is in unit of laser wave length.The transverse flow speed equals ion sound speed.

圖5 對比時間束勻滑光束在調制頻率為 1 0?4ω0 時的光束傳播行為 (a)等離子體橫向流速為零; (b)等離子體橫向流速等于離子聲速.圖中橫縱坐標對應模擬空間坐標y和z, 其量綱為激光波長Fig.5.Propagation of SSD beam at modulation frequency of 10–4w0: (a) No transverse flow; (b) the transverse flow speed equals ion sound speed.x and y axes of two figures corresponding to y and z axes of simulation coordinates, respectively.The spatial scale is in unit of laser wave length.

綜上理論分析和模擬結果都表明, 當SSD光束帶寬遠大于成絲穩定性最大增長率時, 通過抑制成絲不穩定性發展, 可抑制束偏折現象出現.

5 結 論

通過對高斯型光束發生束偏折所需條件進行引申, 提出了束勻滑光束發生束偏折的條件, 并應用數值模擬程序進行了驗證和研究.模擬證實, 對于空間束勻滑激光和時間束勻滑激光來說, 只有同時滿足發生成絲不穩定性和存在離子聲速量級的橫向流時, 才會產生顯著的束偏折現象.這表明束勻滑光束發生束偏折的物理成因與高斯型光束類似, 即成絲不穩定性產生的密度空間結構變化——“凹坑”, 以及在等離子體橫向流作用下產生橫向移動.結合初步理論分析表明, 橫向流速為離子聲速時束偏折現象最顯著.

研究表明, 在均勻等離子體及存在離子聲速量級橫向流時, 如果空間束勻滑光束入射光斑平均光強大于成絲閾值, 可引發成絲不穩定性從而發生束偏折現象; 對于時間束勻滑光束, 當其帶寬遠大于成絲不穩定性最大增長率時, 可以抑制成絲不穩定性從而避免束偏折現象產生, 反之則會發生束偏折現象.