基于MATLAB的牛頭刨床機構運動分析

季佳俊

（河南理工大學 機械與動力工程學院，河南 焦作 454000）

牛頭刨床是用刨刀對工件的平面、溝槽或成形表面進行刨削的直線運動機床，主要用于平面的刨削式加工。其主要由曲柄搖桿機構和滑塊機構構成，加工時工作臺上的工件固定不動，刨刀做平面往復運動，加工工件。當刨頭右行時，刨刀進行切削，稱為工作行程。當刨頭左行時，刨刀不切削，稱為空回行程。對刨床運動機構進行運動學和動力學分析是下一步對牛頭刨床在工作過程中各桿件進行強度分析的基礎，也是進行刨床機構設計的重要參考。

1 牛頭刨床機構的運動學分析

牛頭刨床機構簡圖如圖1所示，該牛頭刨床的運作過程可看作原動件桿O2A以勻角速度繞O2點處的固定鉸支座做定軸轉動，并且帶動從動件桿O4A繞固定鉸支座O4擺動，然后帶動桿BC做平面運動，最終帶動構件6和刨刀P在水平導軌上做往復運動，使刨刀P完成對工件的刨削加工。

圖1 牛頭刨床機構簡圖

1.1 位置分析

在圖1所示的機構簡圖中，以O4點為坐標原點建立平面直角坐標系，標出各桿矢量及其方位角。利用兩個封閉圖形O2O4A和O4BCG（G點為O4O2延長與滑塊C運動導軌的交點），分別建立矢量方程為

將（1）式分別向x軸和y軸投影可得

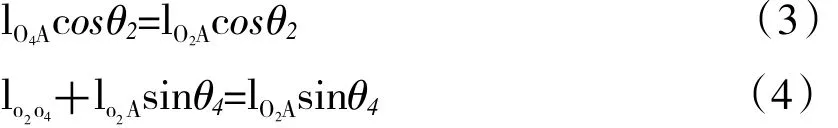
將（2）式分別向x軸和y軸投影可得

式中 θi為各桿矢量的方位角，i=2，4，5;lGC為滑塊C的位移。

由（3）式和（4）式即可求得導桿2的方位角和滑塊3在導桿 4上的位置，代入（5）式和（6）式，即可求得導桿4的方位角和滑塊C的位置。

1.2 速度分析

將（3）式～（6）式對時間求一階導數，并寫成矩陣形式，即可得以下速度矩陣：

其中：

由（7）式可得到滑塊C的速度υC和滑塊3的相對速度υAO4，桿4的角速度ω4和桿5的角速度ω5。

1.3 加速度分析

將（7）式對時間求一階導數，即可得到加速度矩陣：

由（8）式可得到滑塊C的加速度αC，桿4的角加速度α4和桿5的角加速度α5。

牛頭刨床機構中的構件6的運動即為刨床中刀具P的運動，機構各桿件尺寸及重量如表1所示，利用MATLAB輸出得到的刀具的運動學分析曲線如圖2所示，從數據中得到刀具的最大速度為：+1.3826m/s（正號表示方向水平向左），最大加速度為：-9.0278m/s2（負號表示加速度方向和速度方向相反）。刀具P在加工過程中會受到因加速度引起的慣性力而產生的柔性沖擊，所以分析時還要考慮構件的受力產生的影響。

表1 各構件尺寸及重量

如圖2所示，從速度曲線圖可以知道，當桿lO2A從初始的極限位置到圓周運動的最高點時速度逐漸減小，越過最高點后速度開始逐漸增大，通過最低點后速度又會開始減小，機構做急回運動，以縮短刨刀回程的時間，完成一個刨削運動。

從加速度曲線圖可以知道，當桿lO2A從初始的極限位置到桿lO2A第二次與桿lO4B垂直，此時為死點位置，加速度最小，越過死點位置后，加速度開始逐漸增大，通過圓周運動最低點后加速度又會開始減小，完成一個刨削運動。

2 牛頭刨床機構的動力學分析

牛頭刨床機構對工件進行刨削加工，其對桿件受力的要求較嚴格，同時機構受到的約束反力是對其進行強度分析的基本要素。通過運動學分析得到各構件的質心角速度和加速度數據，可求出構件4和構件6的慣性力FI4，FI6和慣性力偶矩MI4，MI6。在用矩陣法對導桿機構進行分析時，通過分別建立以O4為原點的平面直角坐標系，然后將整個機構分為兩個二級基本桿組和一個原動件，分別對各個基本桿組列出力平衡方程，對于任意基本桿組，都列出3個力平衡方程式，因此導桿機構可列出6個力平衡方程式，得到各運動副的約束反力如圖3所示。

圖2 滑塊C的運動曲線分析圖

圖3 運動副反力曲線

如圖3所示，因為切削阻力只在刨刀切削工件時存在，空回行程時為零，所以各運動副反力在一個工作周期內會有迅速變化，同時由于切削阻力作用于水平方向，所以圖中X方向上力的變化較大。

3 利用動能定理求解平衡力矩

為了減少在一個工作過程中由于切削阻力帶來的轉軸速度的周期性波動，通常利用飛輪的畜能的性質進行調速，從而減小電機負擔提高刨削質量，飛輪的設計參量通常是通過對平衡力矩的計算得到的。通過動能定理列出能量方程，等式左邊是微元時間段內機構的總動能改變量，右邊是該時間段內外力的總功率。左邊對時間求導可得平衡力矩的表達式。

化簡得：

將上式數據代入MATLAB中得到平衡力矩圖如圖4所示。

圖4 平衡力矩曲線圖

如圖4所示，由于整個工作過程中切削阻力的變化，平衡力矩分別在曲柄2轉角位于191°和350°處發生改變，其中平衡力矩最大值為849.864Nm（逆時針為正），最小值為-113.498Nm（負號表示與正方向相反）。

4 結語

為了得到牛頭刨床機構運動學和動力學規律，首先對牛頭刨床機構進行運動學分析和動力學分析，通過列出其矢量方程，然后借助MATLAB，以獲得其運動學和動力學特性，并將結果可視化，以獲得刨刀的位移、速度、加速度、和各桿件的約束反力隨原動件lO2A轉動角度變化的規律，最后利用動能定理求出平衡力矩。