進口集裝箱堆存和翻箱策略兩階段規劃模型

游鑫夢 梁承姬 張悅

摘要：為提高進口集裝箱提取作業效率，制定合理的堆存策略和翻箱策略，考慮集裝箱堆存作業與提取作業的關聯性建立兩階段規劃模型。從降低期望翻箱率的角度，優化進口集裝箱的箱位分配，構建第一階段箱區貝位分配模型，并采用遺傳算法求解。基于第一階段的箱區貝位分配結果，在提箱順序已知的情況下，優化障礙箱的落箱位，構建第二階段提箱優化模型，并設計啟發式算法求解。通過算例將該算法與已有算法進行對比，結果表明設計的算法在降低貝內二次翻箱率的效果上更顯著，進而表明提出的兩階段規劃模型能有效降低翻箱率，提升進口集裝箱提取作業效率。

關鍵詞： 進口集裝箱; 堆存策略; 翻箱策略; 啟發式算法

Abstract： In order to enhance the efficiency of import container picking-up operation and formulate reasonable storage and re-handling strategies， a two-stage programming model is established with the consideration of the relationship between storage and picking-up operations of containers. From the point of view of reducing the expected re-handling rate， the position allocation of import containers is optimized， and the bay-in-block allocation model of the first stage is constructed and solved by the genetic algorithm. Based on the bay-in-block allocation results of the first stage and the known picking-up order of containers， the positions of obstacle containers are optimized， and an optimization model of container picking-up operation of the second stage is constructed and solved by the designed heuristic algorithm. The algorithm is compared with the existing algorithms through examples. The results show that the designed algorithm is more effective in reducing the double re-handling rate， which shows that the proposed two-stage programming model can effectively reduce the re-handling rate and improve the efficiency of import container picking-up operation.

Key words： import container; storage strategy; re-handling strategy; heuristic algorithm

0 引 言

近年來，我國水路運輸業發展迅速，碼頭吞吐量急速上升，導致堆場堆放的集裝箱越來越多，堆場翻箱率居高不下。進口集裝箱（以下簡稱進口箱）進場堆存和提取過程均涉及翻箱問題，而翻箱作業制約了集裝箱作業效率，因此本文目的是制定合理的進口箱堆存和翻箱策略，從降低翻箱率的角度提升進口箱提取效率。

對于集裝箱堆存過程中的箱位分配問題：BAZZAZI等[1]在考慮集裝箱類型的條件下研究了每個時段箱區的集裝箱分配問題，并采用遺傳算法求解;YU等[2]提出非隔離、單周期隔離和多周期隔離3種堆存策略，并對這3種策略進行了對比分析;周鵬飛等[3]提出通過統計箱組堆存時間獲取提箱優先級的方法，對卸船箱組的箱位分配進行優化，并設計了啟發式算法進行求解;嚴偉等[4]基于聚類算法設置出口集裝箱集港堆存規則，并通過仿真進行了驗證;周思方等[5]通過預估箱組提取時間范圍建立了箱位指派模型;梁承姬等[6]基于網絡流方法對箱區分配進行了動態研究，并采用禁忌搜索算法進行求解;武慧榮等[7]以海鐵聯運集裝箱碼頭進出口集裝箱為研究對象，構建了堆場箱區分配模型，并采用模擬退火算法進行求解。

對于集裝箱提取過程中的翻箱問題：文獻[2]借鑒KIM[8]提出的計算期望翻箱量的方法，研究了箱區貝位堆存箱量和棧高與翻箱量之間的關系;LEE等[9]提出一種改進模型來預估編組集裝箱的箱位，并設計了啟發式算法進行求解;徐亞等[10]提出一種啟發式算法及其改進算法，對提箱過程中的翻箱問題進行了優化;PETERING等[11]采用一種新的混合整數規劃模型研究了箱區集裝箱的重定位問題，并采用擴展性的啟發式算法求解;鄭斯斯等[12]通過對多種翻箱規則下的優先級進行排序建立了倒箱路徑優化模型，并采用啟發式算法求解;郭瑞智等[13]考慮提箱過程中場橋作業時間構建了整數規劃模型，并設計了啟發式算法求解。

本文在前人研究的基礎上，從降低堆場翻箱率的角度對進口箱的堆存策略和翻箱策略進行研究。首先，以場橋期望提箱完工時間最短為優化目標，建立第一階段箱區貝位分配模型。其次，基于第一階段進口箱分配優化結果，以翻箱總次數最少為目標，構建第二階段提箱優化模型。通過設計啟發式算法減少對障礙箱的二次操作。最后，借助算例將啟發式算法求解的結果與已有算法求解的結果進行對比，驗證本文提出算法的有效性。

1 問題描述

進口箱從待卸船舶被卸載，并被送入堆場進行堆存。根據文獻[8]的研究結論，箱區貝位堆存箱量和棧高與翻箱量之間存在定量關系，而且可以預估進口箱在提取過程中的期望翻箱量。因此，進口箱的堆存優化需要在箱區貝位合理分配集裝箱堆存量，降低箱區首次翻箱率。

在上述研究的基礎上獲取貝內集裝箱的堆存量。將每個階段需取走的集裝箱記作目標箱，將目標箱上方的集裝箱記作障礙箱，則優化障礙箱的落箱位置是降低貝內二次翻箱率的關鍵。

針對障礙箱的落箱位置選擇問題，設計提箱作業啟發式算法。設障礙箱的提箱優先級為p0，障礙箱落箱候選堆棧的優先級選擇順序如下：（1）若某堆棧內堆放的集裝箱的最高優先級低于p0，則該堆棧為障礙箱落箱最優堆棧;（2）空棧為障礙箱落箱次優堆棧;（3）比較每個堆棧現有集裝箱的最高優先級，選擇集裝箱最高優先級值最低的堆棧為障礙箱落箱末優堆棧。若以上每種類型的堆棧存在多個，則優先考慮鄰近堆棧上的空箱位為障礙箱落箱位置。本文中提箱優先級指提箱先后次序，依該次序為集裝箱編號。

綜上所述，進口箱堆存和提取均涉及翻箱問題，且兩個過程相互關聯。本文從堆存和提取方面進行兩階段研究。第一階段以單箱區為研究對象，確定在初步降低箱區期望首次翻箱率的同時，優化箱區各貝位的進口箱量分配。第二階段在箱區各貝位集裝箱堆存狀態和提取順序已知的情況下研究貝內翻箱問題。通過優化障礙箱的落箱位置進一步降低貝內二次翻箱率。本文建立進口箱堆存和提取兩階段規劃模型來實現上述過程。

2 進口箱堆存和提取兩階段規劃模型

2.1 第一階段箱區貝位分配模型

2.1.1 模型假設

某時段被分配到箱區的集裝箱量已知;集裝箱進入堆場時，分配到箱區各貝位的概率相同;貝位堆棧的最大層數為H時，為滿足所有情況下障礙箱的落箱需求，貝內需留有H-1個空箱位;在無懸臂軌道吊的箱區布局中，只有一臺場橋進行作業。

2.1.2 模型參數與變量

已知參數：Cu表示在某時段內分配到箱區的卸船箱總量;n表示箱區的貝位總數;i表示貝位編號（i=1，2，…，n）;S表示貝位最大堆棧數（s=1，2，…，S）;H表示貝內堆棧最大層數（h=1，2，…，H）;C表示貝位堆放集裝箱的最大容量;Coi表示貝位i的初始集裝箱堆存量;to表示場橋單位翻箱作業時間;tc表示場橋單位提放箱作業時間;tm表示場橋單貝位移動時間;R（C）表示當貝內集裝箱堆存量為C時，提取所有集裝箱的預估期望翻箱量。

決策變量：Ci表示從船舶卸載的集裝箱分配到箱區貝位i的箱量。

2.1.3 貝位期望翻箱量估計

借鑒文獻[8]估計貝位期望翻箱量的方法，研究得出箱區每個貝位期望翻箱量與堆存箱量和棧高有關。當貝位最大堆棧數S已確定時，根據貝位的堆存箱量C計算提箱過程中產生的平均翻箱量R（C）。

2.1.4 箱區貝位分配模型

以場橋期望提箱完工時間最短為目標，建立箱區貝位分配模型如下：

式（2）為目標函數，表示目標是箱區場橋期望提箱完工時間（由場橋期望翻箱作業時間、移動時間和提放箱作業時間組成）最短，第一項中R（Coi+Ci）-RCoi表示貝位i新增的期望翻箱量;式（3）保證分配到各貝位的箱量之和等于卸船進口箱總量;式（4）表示當堆棧最底層的集裝箱出現翻箱作業時，確保貝內有充足的空箱位提供，即限制貝內集裝箱的分配數量不超過其最大容量;式（5）是對決策變量的取整約束。

2.2 第二階段提箱優化模型

2.2.1 模型假設

貝內堆存的集裝箱均為20英尺（1英尺≈0.304 8 m）的標準箱;考慮場橋作業的安全性，翻箱限制在同一貝內進行;貝內集裝箱初始堆存狀態和提取順序已知;進行提箱作業時，不考慮新的集裝箱入貝堆存。

2.2.2 模型參數與變量

已知參數：根據上述箱區貝位分配模型，可得到貝內集裝箱堆存量C。在本階段研究中，共同參數部分與第一階段模型中的一致，其他具體參數有：集裝箱的提箱優先級p（p=1，2，…，P）、障礙箱的提箱優先級p0、提箱階段l（l=1，2，…，L）、貝內集裝箱的初始堆存狀態Ipsh（表示提箱優先級為p的集裝箱堆存在堆棧s的第h層）。

決策變量：xlpsh，若第l階段提箱優先級為p的集裝箱堆存在堆棧s的第h層，則其值取1，否則為0;ylpshab，若第l階段提箱優先級為p的集裝箱從堆棧s的第h層被翻至堆棧a的第b層，則其值取1，否則為0;zlpsh，若第l階段提箱優先級為p的集裝箱被從堆棧s的第h層提走，則其值取1，否則為0。

2.2.3 提箱優化模型

基于上述參數和決策變量，以貝內翻箱總次數最少為目標，建立進口箱提箱優化模型：

式（7）表示貝內集裝箱初始堆存情況與第0階段的堆存情況一致;式（8）表示每次操作只作業一個集裝箱，且該集裝箱只能被提取或被翻倒至其他堆棧[14];式（9）表示若某個階段產生翻箱作業，則為障礙箱選擇的落箱位必須是空箱位;式（10）等號右邊第2項和第3項表示提箱過程中翻箱操作對位置變量xlpsh的影響，第4項表示提箱操作對xlpsh的影響[15];式（11）表示在堆存集裝箱或翻箱過程中不能出現懸空位置;式（12）確保貝內所有集裝箱最終被提取完畢;式（13）表示任一提箱優先級為p的集裝箱在貝內均有確定的箱位，或已被提取離場，或仍堆存在貝內;式（14）表示貝內任一箱位最多只能堆放一個集裝箱;式（15）表示按照既定的提箱順序依次提箱;式（16）表示決策變量的取值范圍。

3 模型求解

根據模型的特點，對第一階段箱區貝位分配模型采用遺傳算法進行求解，對第二階段提箱優化模型設計啟發式算法來求解。兩種求解方法均在MATLAB平臺上操作運行。

3.1 遺傳算法主要求解步驟

（1）初始種群。在進行編碼時采用整數編碼的形式，假設箱區貝位數為n，需要生成n個貝位的分配量，即染色體可以表示為：C1，C2，C3，…，Cn。其中，基因值C1，C2，C3，…，Cn分別對應箱區各貝位進口箱的箱量分配。圖1為染色體編碼示例。

（2）適應度函數和選擇策略。目標為場橋期望提箱完工時間最短，因此取目標函數的倒數作為適應度函數。

采取精英保留策略，即在父代種群中選擇適應性強的個體插入子代種群中，從而保證子代中一定存在優于上一代的個體。

（3）交叉。對每代種群以一定的交叉率pc進行染色體交叉。由于染色體設計的特殊性，參考文獻[1]中的線性組合交叉策略，線性組合系數為k，在兩個個體P1，g、P2，g之間進行算術交叉，產生新的個體。計算方式如下：

圖2為父代（第g代）染色體交叉示例：箱區設置10個貝位，分配到箱區的進口箱總量為100 TEU，P1，g和P2，g為兩條父代染色體。當k=0.85時，子代P1，g+1在1號貝位的數值為：0.85×9+0.15×8=8.85。按照此方法計算其余位置數值從而得到子代P1，g+1。子代P2，g+1在1號貝位的數值為：0.85×8+0.15×9=8.15。采取相同的方式得到子代P2，g+1。為滿足染色體的基因值為正整數，線性交叉后子代個體采用奇數貝位對應的基因值向負無窮方向取整，偶數貝位對應的基因值向正無窮方向取整的方式進行保留。基因修復后子代P1，g+1在1號貝位的數值為8，子代P2，g+1在1號貝位的數值為8。若基因總值不等于100，則在超過或小于額定值的染色體中尋找最大或最小的基因值，并進行相應的刪減或增加，從而使得染色體滿足條件。

（4）變異。對每代種群以一定的變異率pm進行染色體變異。變異方式采用將兩個父代染色體上相同基因位置的進箱量相互置換，同時重新獲得箱區各貝位所對應的進口箱分配量。

（5）結束規則。當算法迭代到設定的最大次數時，結束并輸出結果。

3.2 提箱作業啟發式算法

貝內集裝箱在被提取之前均有確定且唯一的優先級別。視一個優先級別的集裝箱為一個提箱階段。當提箱過程中出現翻箱操作時，需尋找其余未滿額定層數的堆棧，作為翻出障礙箱的可落堆棧集。為障礙箱選擇合適的落箱堆棧是降低二次翻箱率的關鍵，而可落堆棧集中包含以下6種堆存情形：（1）僅有一個堆棧內現有集裝箱最高優先級低于p0，且無空棧;（2）與情形1的類似，但有多個滿足條件的合適堆棧;（3）存在某堆棧內現有集裝箱最高優先級低于p0的情況，也存在空棧;（4）存在空棧且唯一，而不存在某堆棧內現有集裝箱最高優先級低于p0的情況;（5）存在多個空棧，而不存在某堆棧內現有集裝箱最高優先級低于p0的情況;（6）除以上5種情形之外的其他堆存情況。

確定貝內每個提箱階段目標箱所存箱位，將可落堆棧集中包含的6種堆存情形設置成相應的落箱規則，并將其嵌套至提箱作業過程中;外集卡依次到港，提取已經獲得優先級的集裝箱。嵌套落箱規則的提箱作業啟發式算法流程見圖3。

4 算 例

4.1 第一階段箱區貝位分配模型求解

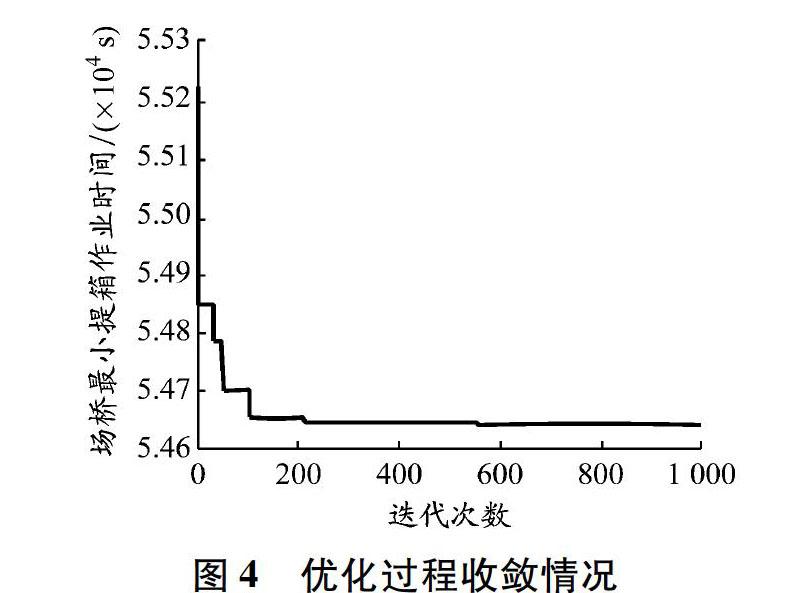
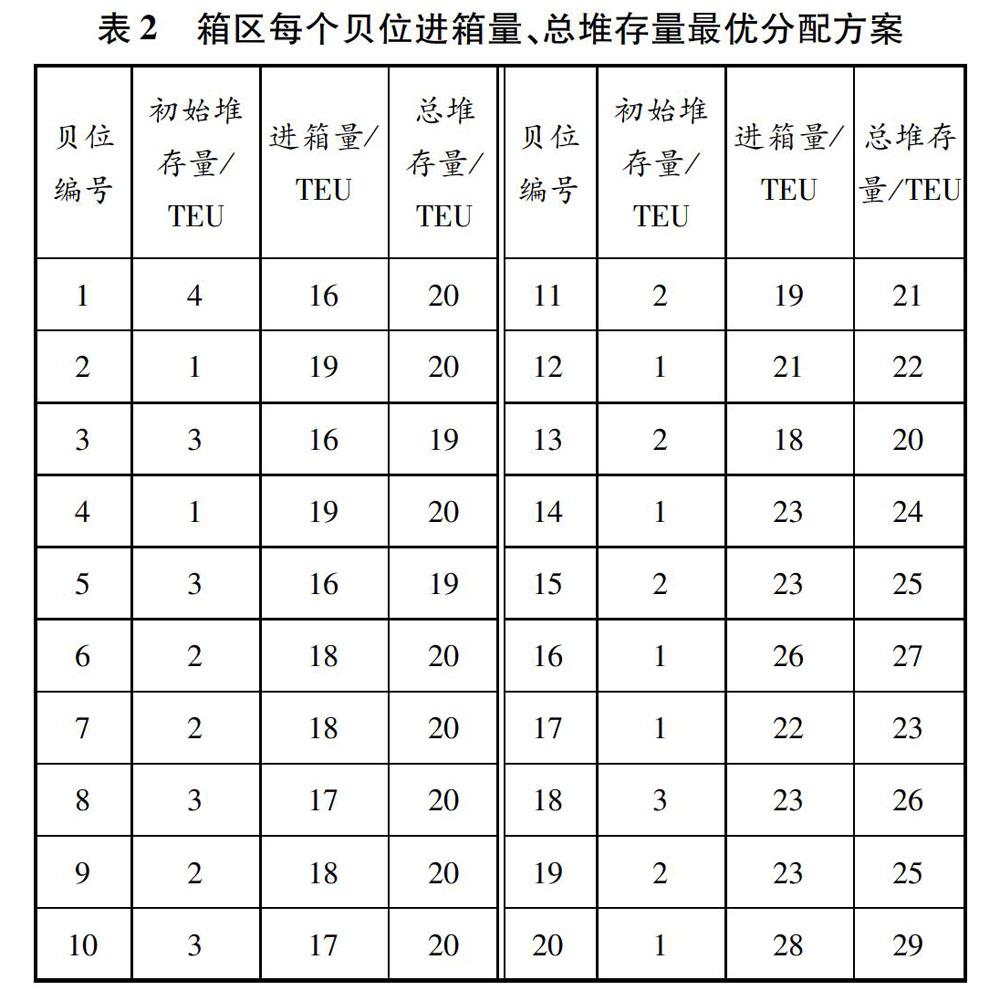
以自動化碼頭單箱區為研究對象，參數設置見表1。箱區每個貝位初始集裝箱堆存量已知，見表2。遺傳算法中：最大迭代次數設為1 000;種群規模設為100（100條染色體）;交叉系數pc設為0.85;變異系數pm設為0.15;交叉線性組合系數k設為0.8。應用MATLAB R2018a編程環境，使用遺傳算法計算10次，取最優的收斂效果，見圖4。當算法迭代至第550次時，目標函數值趨向收斂，用時約54 638 s，場橋期望提箱完工時間達到最短。當目標函數值最小時，對應決策變量的最優結果見表2，例如，1號貝位所分配的進口箱最優箱量為16 TEU，總堆存量最優結果為20 TEU。

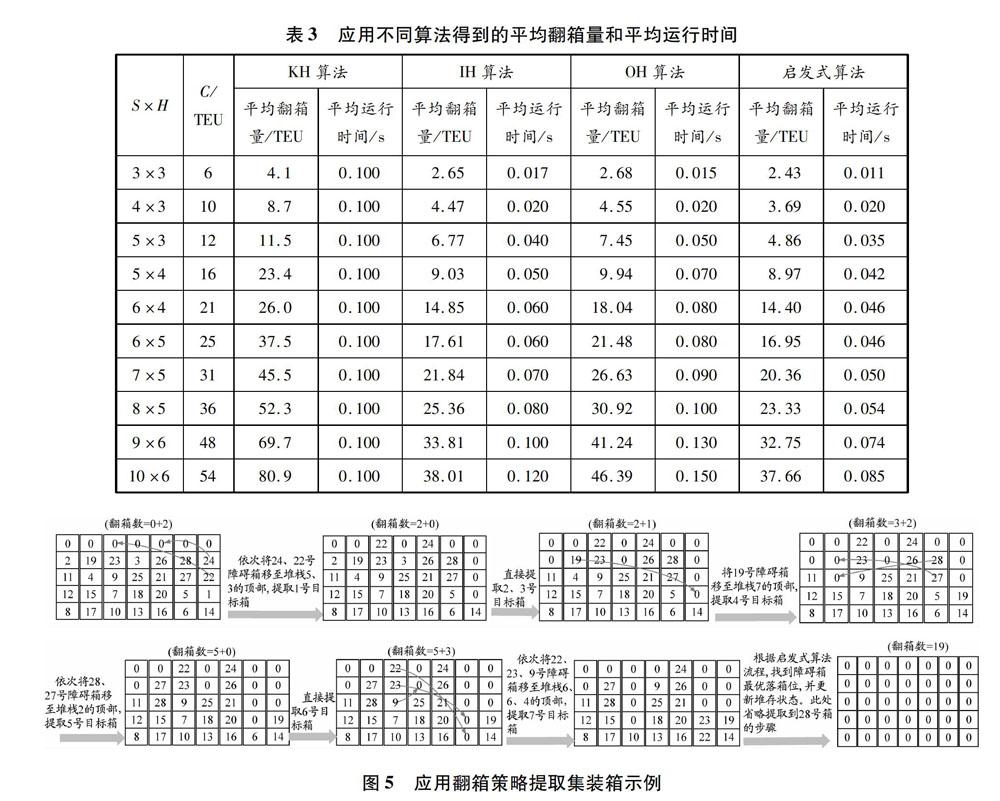
4.2 第二階段提箱優化模型求解

在提箱優化問題上，為驗證所設計的啟發式算法的有效性，采用MATLAB R2018a編程將本文提出的啟發式算法與KH算法[16]、IH算法[10]和OH算法[14]的運行結果進行對比。選取10種不同的貝位規模，并在每種規模下隨機生成100個算例實驗，最后以平均翻箱量和平均運行時間這兩個指標評比算法的性能，見表3。第二階段進一步落實到在提箱過程中對貝內集裝箱的翻箱問題，基于第一階段箱區貝位分配模型的求解結果，取其中優化的進箱量為28 TEU的貝位進行研究，應用翻箱策略提取集裝箱的示例見圖5。集裝箱上的編號表示提箱優先級，0表示空箱位。當場橋提取1號集裝箱時，存在壓箱現象，需依次將24號和22號箱翻倒至同貝的其他堆棧。根據提箱作業啟發式算法，結合當前階段貝內集裝箱的堆存狀態，直接將24號和22號集裝箱分別移至堆棧5和3的頂部。

當目標箱上的障礙箱全部翻倒后，場橋可提取1號箱離場。同理，應用設計的啟發式算法，依次提取每個提箱階段的目標箱，最終將貝內集裝箱提取完畢。

4.3 結果分析

第一階段優化以單箱區為研究對象，目標是降低箱區首次翻箱率。當場橋的期望提箱完工時間最短時，從船舶卸載的集裝箱分配到箱區的箱量在每個貝位內大致呈現均衡性。而由于場橋的單位翻箱作業時間遠大于其在單位貝位內的移動時間，故箱區內鄰近陸側貝位的進箱量比海側端口的多。

第一階段僅僅從研究堆存策略的角度，初步使堆場箱區首次翻箱率得到降低。在進行第二階段提箱優化后，通過合理設計障礙箱倒箱落位的啟發式算法，并結合算例表明，即使擴大貝位規模，本文設計的啟發式算法在翻箱量和程序運行時間上也優于已有算法，驗證了本文算法的有效性。因此，可將設計的算法應用于提箱過程中，進一步降低堆場二次翻箱率。

5 結 論

本文為制定合理的堆存與翻箱策略，對進口箱堆存與提取過程進行了優化研究，并考慮兩個過程的關聯性，構建了兩階段規劃模型。第一階段以場橋期望提箱完工時間最短為目標，在初步降低箱區期望首次翻箱率的情況下，建立箱區貝位分配模型進行堆存優化。將第一階段求解的貝位進箱分配結果作為輸入，并在集裝箱堆存狀態和提箱順序已知的條件下，優化障礙箱的落箱位，建立第二階段提箱優化模型，并設計啟發式算法進行求解。該算法與已有算法的對比結果表明，應用該算法降低貝內二次翻箱率的效果更顯著，從而表明提出的兩階段模型能夠降低堆場翻箱率，使進口箱提箱作業效率得到提升。

參考文獻：

[1]BAZZAZI M， SAFAEI N， JAVADIAN N， et al. A genetic algorithm to solve the storage space allocation problem in a container terminal[J]. Computers & Industrial Engineering， 2009， 56： 44-52. DOI： 10.1016/j.cie.2008.03.012.

[2]YU Mingzhu， QI Xiangtong. Storage space allocation models for inbound containers in an automatic container terminal[J]. European Journal of Operational Research， 2013， 226： 32-45. DOI： 10.1016/j.ejor.2012.10.045.

[3]周鵬飛， 李丕安. 集裝箱堆場不確定提箱次序與卸船箱位分配[J]. 哈爾濱工程大學學報， 2013， 34（9）： 1119-1123. DOI： 10.3969 /j.issn.1006-7043.201301022.

[4]嚴偉， 朱夷詩， 黃有方， 等. 基于聚類分析的集裝箱碼頭堆場策略[J]. 上海海事大學學報， 2014， 35（1）： 35-40， 59. DOI： 10.13340 /j.jsmu.2014.01.008.

[5]周思方， 張慶年. 基于提箱同步的進口箱堆存策略研究[J]. 交通運輸系統工程與信息， 2018， 18（5）： 151-157. DOI： 10.16097/j.cnki.1009-6744.2018.05.022.

[6]梁承姬， 賈茹， 盛揚. 基于網絡流的自動化集裝箱碼頭堆場空間分配[J]. 計算機應用與軟件， 2018， 35（1）： 77-84. DOI： 10.3969 /j.issn.1000-386x.2018.01.013.

[7]武慧榮， 朱曉寧， 鄧紅星. 集裝箱海鐵聯運港口混堆堆場箱區均衡分配模型[J]. 重慶交通大學學報（自然科學版）， 2018， 37（4）： 109-115. DOI： 10.3969 /j.issn.1674-0696.2018.04.17.

[8]KIM K H. Evaluation of the number of rehandles in container yards[J]. Computers & Industrial Engineering， 1997， 32（4）： 701-711.

[9]LEE Yusin， CHAO Shih-Liang. A neighborhood search heuristic for pre-marshalling export containers[J]. European Journal of Operational Research， 2009， 196： 468-475. DOI： 10.1016/j.ejor.2008.03.011.

[10]徐亞， 陳秋雙， 龍磊， 等. 集裝箱倒箱問題的啟發式算法研究[J]. 系統仿真學報， 2008， 20（14）： 3666-3669， 3674. DOI： 10.16182/j.cnki.joss.2008.14.006.

[11]PETERING M E H， HUSSEIN M I. A new mixed integer program and extended look-ahead heuristic algorithm for the block relocation problem[J]. European Journal of Operational Research， 2013， 231： 120-130. DOI： 10.1016/j.ejor.2013.05.037.

[12]鄭斯斯， 王愛虎. 路徑優化算法求解集裝箱碼頭堆場翻箱問題[J]. 工業工程與管理， 2017， 22（3）： 31-40. DOI： 10.19495/j.cnki.1007-5429.2017.03.005.

[13]郭瑞智， 史瑪君， 林昊堃. 集裝箱倒箱問題的模型與啟發式算法研究[J]. 數學雜志， 2017， 37（4）： 805-810. DOI： 10.13548/j.sxzz.2017.04.005.

[14]KIM K H， HONG G-P. A heuristic rule for relocating blocks[J]. Computers & Operations Research， 2006， 33（4）： 940-954. DOI： 10.1016/j.cor.2004.08.005.

[15]朱明華， 程奐翀， 范秀敏. 基于定向搜索算法的集裝箱堆場翻箱問題[J]. 計算機集成制造系統， 2012， 18（3）： 639-644. DOI： 10.13196/j.cims.2012.03.193.zhumh.013.

[16]KIM K H， KIM H B. Segregating space allocation models for container inventories in port container terminals[J]. International Journal of Production Economics， 1999， 59： 415-423.

（編輯 賈裙平）