一種改進(jìn)的頻移鍵控調(diào)制信號盲識別方法研究*

席建民，邱 濤，吉 磊

（中國電子科技集團(tuán)公司第三十研究所，四川 成都 610041）

0 引 言

頻移鍵控（FSK，F(xiàn)requency Shift Keying）信號是一種以數(shù)字序列控制載波頻率變化的調(diào)制信號。根據(jù)已調(diào)相位是否連續(xù)，頻移鍵控可分為兩類：連續(xù)相位頻移鍵控和非連續(xù)相位頻移鍵控。由于較易實(shí)現(xiàn)，抗噪與抗衰減性能良好等特點(diǎn)，因此在民用和軍事通信領(lǐng)域中都得到了廣泛的應(yīng)用，如跳頻電臺網(wǎng)、無人機(jī)遙控系統(tǒng)、關(guān)鍵基礎(chǔ)設(shè)施及物聯(lián)網(wǎng)射頻傳輸系統(tǒng)和美軍Link4A 數(shù)據(jù)鏈等。頻移鍵控信號調(diào)制識別是進(jìn)行后續(xù)解調(diào)的基礎(chǔ)，分析得到的頻移鍵控調(diào)制樣式具有重要意義，作用也十分廣泛。對調(diào)制信號進(jìn)行成功識別可運(yùn)用于認(rèn)知無線電，干擾信號識別，電磁頻譜管理，通信偵察等方面，尤其是認(rèn)知無線電的設(shè)計和推動已被公認(rèn)為無線電領(lǐng)域里能感知環(huán)境并作出智能響應(yīng)，滿足頻譜接入效率和可靠性需求增加最有希望的解決方案，而調(diào)制識別即為認(rèn)知無線電系統(tǒng)的一個關(guān)鍵環(huán)節(jié)，尤其是對于認(rèn)知無線電環(huán)境監(jiān)測方面，識別出信號的調(diào)制樣式極有助于成功地進(jìn)行頻譜感知以及自主學(xué)習(xí)。調(diào)制類型盲識別算法通常有基于假定檢驗(yàn)的最大似然識別思路與基于特征提取的統(tǒng)計模式識別思路[1]，其中基于假設(shè)檢驗(yàn)的識別方法的判斷法則相對較簡單，但缺點(diǎn)是運(yùn)算量很大且必須獲取到調(diào)制信號的先驗(yàn)信息，不易進(jìn)行實(shí)時處理，魯棒性差；故目前比較普遍采用的是基于特征提取的識別方法，便于計算且能根據(jù)提取出的信號特征完成判別，相對更簡單。

由于在實(shí)際復(fù)雜環(huán)境中存在各種噪聲和干擾信號，并非所有的特征都可用于正確識別信號的調(diào)制樣式，因此，尋求有效的信號特征參數(shù)并探索更好的調(diào)制識別方法已引起了國內(nèi)外許多研究人員和學(xué)者的關(guān)注。過去的一些基于特征提取的統(tǒng)計模式識別方法有：使用功率譜特征識別、信號時頻域特征識別、信號瞬時頻率及相位特征識別等。例如Nandi 提出了一種基于多種瞬時特征參數(shù)的模擬調(diào)制和數(shù)字調(diào)制識別算法，該算法可一定程度上識別5 種調(diào)制樣式，但對信噪比因素很敏感，性能急劇下降[2]；K.C.Ho 等人設(shè)計了基于小波變換的識別思路，該算法的問題是識別的調(diào)制種類有限，且變換的尺度與信號碼速率有關(guān)，導(dǎo)致特征量值易受影響[3]；郭雙冰研究了一種基于混沌時間序列預(yù)測及混沌理論的方法，不足之處是計算復(fù)雜度高，且需要的信號樣本點(diǎn)數(shù)較多[4]。

針對上述的多方面問題，本文深入分析了各進(jìn)制的M-FSK（M-ary Frequency Shift Keying）信號在低信噪比復(fù)雜電磁環(huán)境中的循環(huán)平穩(wěn)特征，并對其融合提取思路進(jìn)行研究，在此基礎(chǔ)上提出了一種改進(jìn)的頻移鍵控調(diào)制信號盲識別新方法。該算法基于循環(huán)平穩(wěn)統(tǒng)計量特征的計算，得到擴(kuò)展的循環(huán)頻率與循環(huán)矩參數(shù)，具體實(shí)現(xiàn)時采取了優(yōu)化計算的思路。優(yōu)點(diǎn)是不需要先驗(yàn)條件和事先符號定時、載波恢復(fù)等步驟，能較好地適應(yīng)于頻移鍵控信號自身特點(diǎn)，不需要任何先驗(yàn)條件和事先符號定時、載波恢復(fù)等步驟。該算法穩(wěn)健性強(qiáng)，有利于不同調(diào)制指數(shù)頻移鍵控信號的判斷，不僅能正確識別類間調(diào)制信號，也可用于處理類內(nèi)信號，精細(xì)區(qū)分出頻移鍵控信號的不同進(jìn)制階數(shù)。

1 信號模型分析

設(shè)收到的下變頻及濾波處理后的M-FSK 信號基帶波形計算表達(dá)式為：

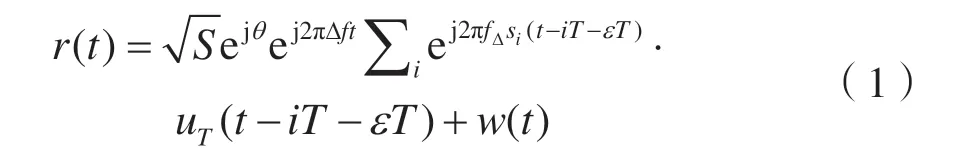
其中，S 表示信號功率，θ 表示載波的相位，Δf 表示載波頻率偏移量，fΔ表示剩余頻差，T 表示符號周期，0 ≤ε<1 代表定時誤差，uT(t)為單位幅度的矩形脈沖響應(yīng)，其幅值為1，持續(xù)時間為T。w(t)表示零均值復(fù)高斯噪聲，其功率為N，si表示在第i 個周期傳輸?shù)姆枺冶硎緩?fù)數(shù)單位。并且數(shù)據(jù)符號{si}被設(shè)為零均值獨(dú)立同分布隨機(jī)變量，其值可根據(jù)M-FSK 調(diào)制信號的定義得出，如：

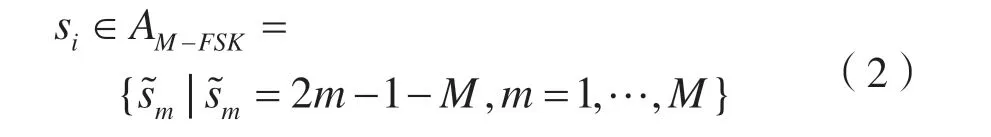
這里的調(diào)制進(jìn)制階數(shù)為M，其值可取為2 的冪。

在接收端，基帶信號的歸一化是相對于接收信號的功率進(jìn)行的，先去除數(shù)據(jù)中可去掉的縮放因子然后以采樣率fs進(jìn)行采樣，從而產(chǎn)生離散時間的歸一化信號如下：

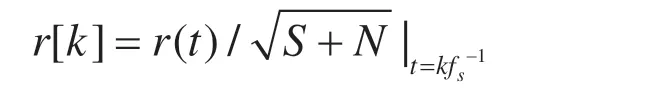
典型的2FSK 信號調(diào)制原理框圖如圖1 所示。

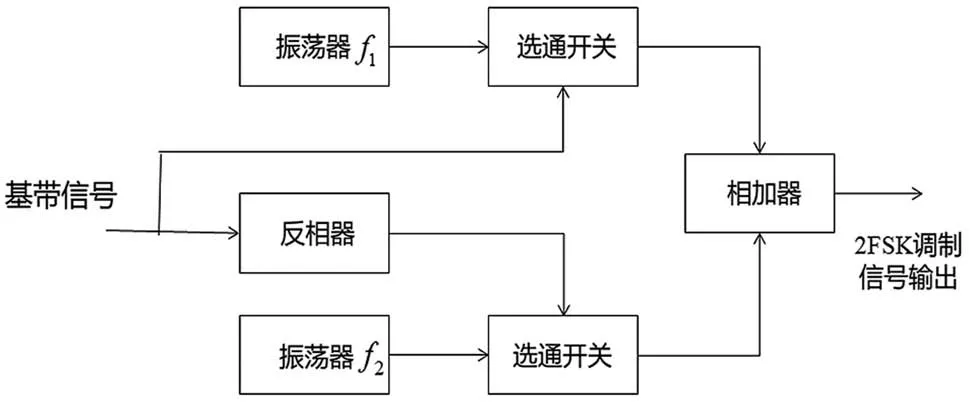
圖1 2FSK 信號調(diào)制原理

圖1 中，采用鍵控法實(shí)現(xiàn)了2FSK 調(diào)制模型，該方法是較容易實(shí)現(xiàn)的一種思路。兩個獨(dú)立的載波振蕩發(fā)生器的輸出f1和f2受控于輸入的基帶二進(jìn)制信號，按照或分別利用選通開關(guān)選擇一個載波作為輸出，可生成FSK 數(shù)字調(diào)制信號。M-FSK 與其它樣式的調(diào)制信號不同，它具有多個載頻信息。在信道化處理流程中，可能將其分離為單頻信號，破壞頻譜的完整性，因此需要分析信號的頻域相關(guān)性，通過其循環(huán)平穩(wěn)特性避免此問題。

下面詳細(xì)分析信號的循環(huán)平穩(wěn)統(tǒng)計量。設(shè)r(t)為典型的非平穩(wěn)連續(xù)時間復(fù)值過程，其一階時變矩可定義為：其中E[·]表示統(tǒng)計期望。若r(t)為一階循環(huán)平穩(wěn)統(tǒng)計過程，則時變矩參量可作為時間的近似周期性函數(shù)。當(dāng)周期函數(shù)經(jīng)過傅里葉級數(shù)計算展開處理后，可用下式表示成：

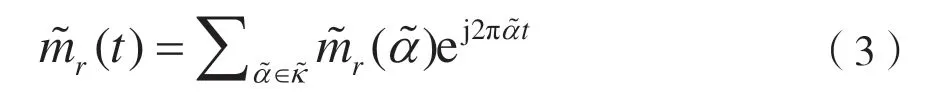
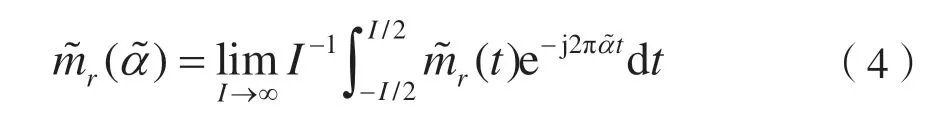
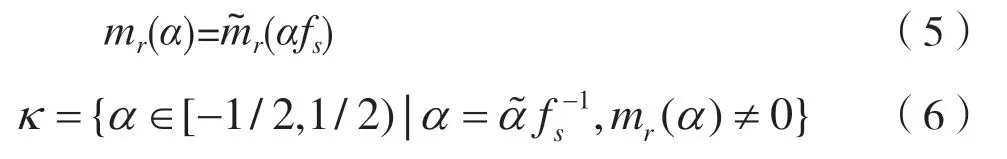
注意到式子里在循環(huán)頻率以外的頻率處循環(huán)矩都為0。可得基于K 個采樣點(diǎn)，在循環(huán)頻率為α 處的一階循環(huán)矩估計器的運(yùn)算表達(dá)式如下：

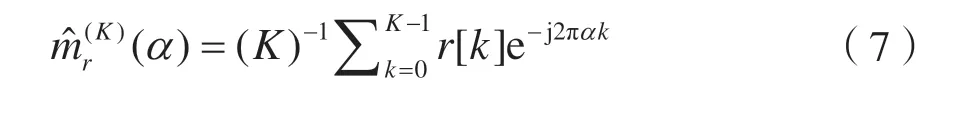
2 識別算法分析

信號識別方法的典型主要流程如圖2 表示。

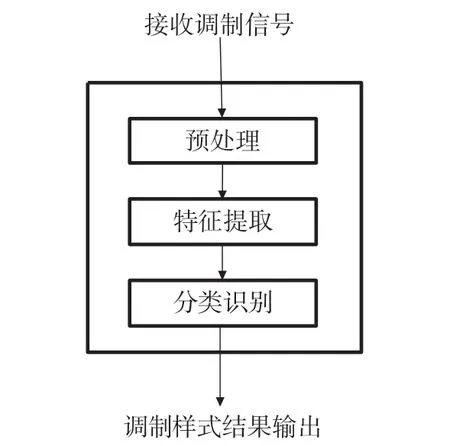
圖2 信號識別的典型主要流程

特征提取模塊的主要作用是獲得能夠顯著表征各種調(diào)制信號之間差異的參數(shù)特征。理想的特征可以非常明顯的區(qū)分不同樣式的調(diào)制信號，而且對于同一種調(diào)制類型信號能夠保持較好的一致性[5]。本文采用信號的循環(huán)平穩(wěn)統(tǒng)計量作為頻移鍵控調(diào)制的關(guān)鍵識別特征，具有很強(qiáng)的穩(wěn)健性。M-FSK 基帶接收信號的循環(huán)平穩(wěn)統(tǒng)計量表達(dá)式為：

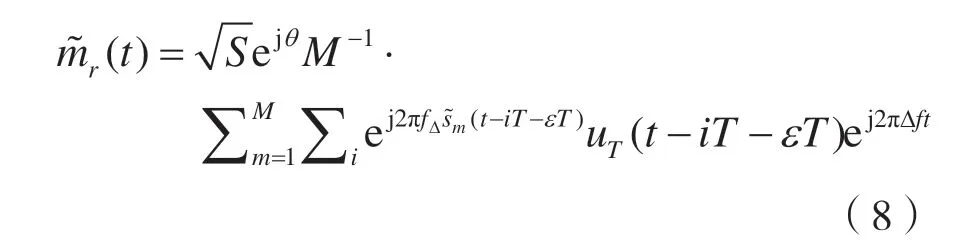
式中，其取平均值是針對未知數(shù)據(jù)符號執(zhí)行的，前提是在第i 個周期內(nèi)的符號在頻移鍵控進(jìn)制階數(shù)映射表中取等概率值。式（8）還可進(jìn)一步寫為：

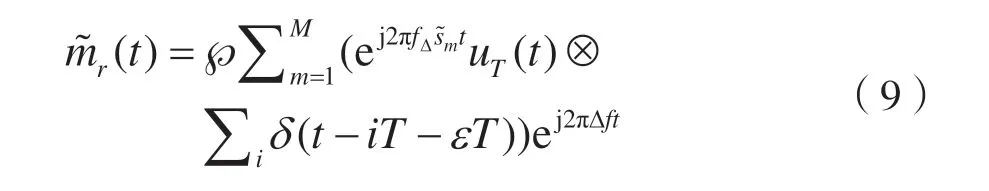
期函數(shù)，其基本周期為T。調(diào)制信號循環(huán)矩可較易的計算展開表示為傅里葉級數(shù)形式。當(dāng)Δf ≠0時，式（9）的傅里葉變換式為：

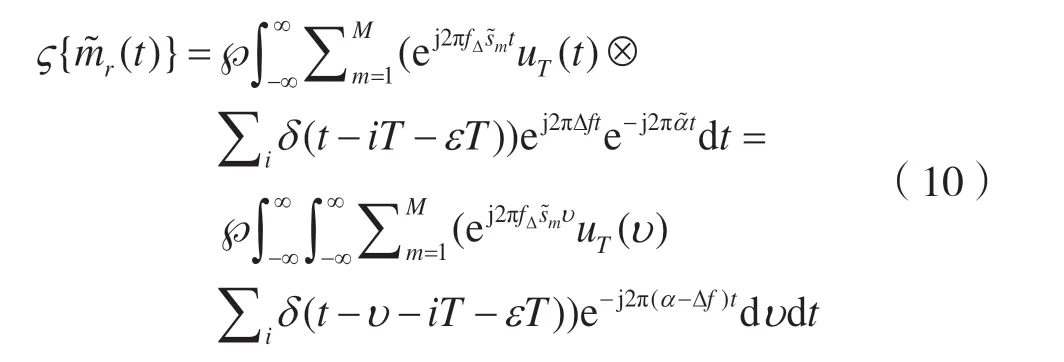
其中， ?{}·表示傅里葉變換，且有：

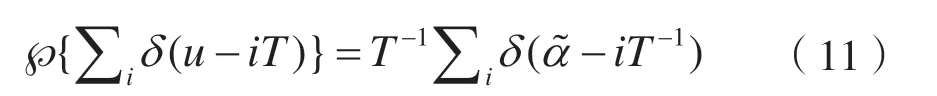
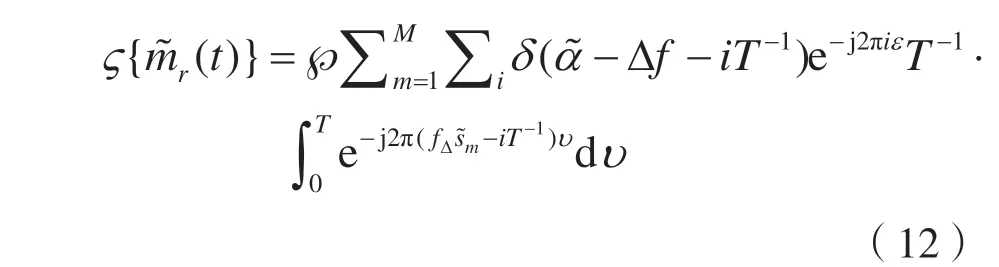
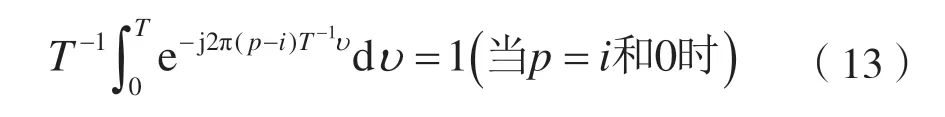
前述計算式（12）可轉(zhuǎn)化為：

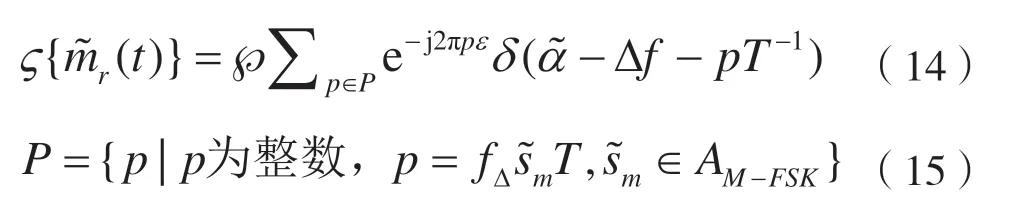
如果fΔ=lT-1，l 為整數(shù)，且易有p=±l,±3l,…,±(M-1)l，此外其循環(huán)譜由M 個有限幅度的附加分量組成，可得：

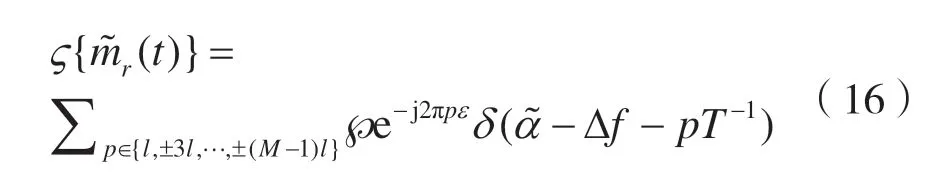
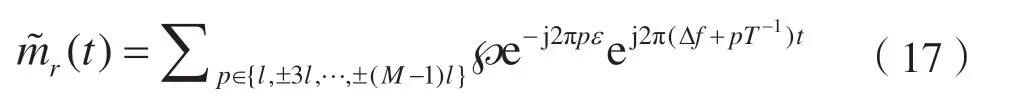
顯然，此處有：

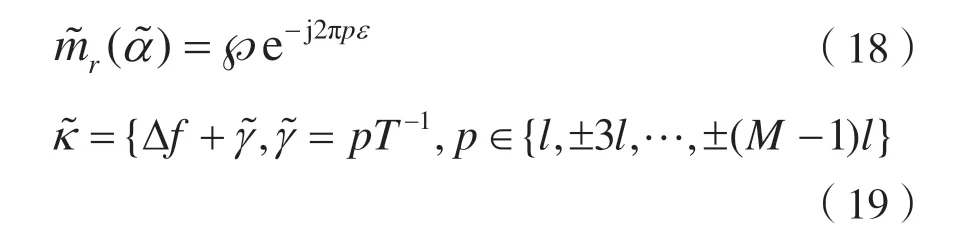
利用之前對連續(xù)時間信號r(t)的計算結(jié)果，并考慮信號歸一化，可以很容易地得到歸一化離散時間信號的表達(dá)式為：

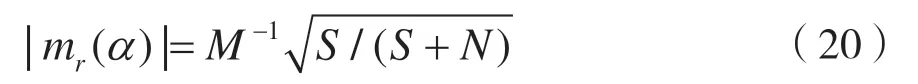
式（20）表示在循環(huán)頻率α 處的循環(huán)矩幅度，取決于調(diào)制的進(jìn)制階數(shù)M 和信噪比SNR，其值隨著M 的增加而減小，隨著SNR 的減小而減小。此外，循環(huán)頻率的數(shù)目等于調(diào)制階數(shù)，并且對于任何給定M，循環(huán)頻率取決于載波頻率偏移量Δf、采樣頻率fs和頻率偏差fΔ[6-7]。

本文設(shè)計了一種提取FSK 信號循環(huán)平穩(wěn)特征的思路，對于復(fù)雜環(huán)境中受噪聲、相偏、頻偏和定時誤差影響的FSK 接收信號也能適應(yīng)。首先對接收信號的帶寬進(jìn)行估計，然后對不同信號在相同帶寬的假設(shè)下進(jìn)行分類，從接收信號中提取循環(huán)頻率的個數(shù)，用于決策分析。接收端也不需要任何接收信號的先驗(yàn)知識。此外，也不須進(jìn)行載波恢復(fù)和符號預(yù)處理。改進(jìn)的新盲識別方法包括以下主要步驟——

（1）基于K 個樣本的觀測間隔對歸一化接收信號的一階循環(huán)矩進(jìn)行估計，選擇在待識別循環(huán)頻率α′位置處，分布范圍為[-1/2,1/2)。根據(jù)理論推導(dǎo)，高斯白噪聲的循環(huán)矩幅值為零，幅度在式（3）中給出的頻率下為非零值，即循環(huán)頻率。當(dāng)依據(jù)有限長的數(shù)據(jù)序列（K 個樣本）估計循環(huán)矩的幅度時，會出現(xiàn)非零的剩余噪聲，在其它位置處也為非零值以外的循環(huán)頻率僅作為基于有限長度數(shù)據(jù)序列的估計結(jié)果出現(xiàn)。另一方面，在循環(huán)頻率處的一階循環(huán)矩幅度隨著信噪比的降低而減小，因此，在一定信噪比下，循環(huán)矩的幅度值可與待識別循環(huán)頻率的非零統(tǒng)計量估計值近似相等。設(shè)置閾值為VCO，使得在微小幅度的循環(huán)矩計算值出現(xiàn)在VCO以下。顯然，接收的數(shù)據(jù)序列長度越長，循環(huán)矩估計值越精確，則在循環(huán)頻率以外的待識別頻率位置處的循環(huán)矩估計值等于零并且VCO的值比可設(shè)置的更低。利用式（20），可以較易得出在循環(huán)頻率處循環(huán)矩幅度等于VCO，其對應(yīng)的判決信噪比SNR 理論閾值，即：

實(shí)際上，當(dāng)SNRSNRCO時，取值則都在VCO以上。并可得到在循環(huán)頻率處的循環(huán)矩幅度的一些估計量低于VCO，然而在SNR取值附近，盡管在小于SNRCO的情況，一些估計量仍大于VCO。

循環(huán)平穩(wěn)特性統(tǒng)計量可用于測量待識別循環(huán)頻率，以Ncf作為待識別循環(huán)頻率的數(shù)目來判決確定是否接收到目標(biāo)信號的循環(huán)頻率，所以基于以下識別分類準(zhǔn)則來決定調(diào)制進(jìn)制階數(shù)：

（1）若M/2+1 ≤Ncf≤M，則FSK 信號的相應(yīng)進(jìn)制階數(shù)為M；

（2）當(dāng)Ncf<2，即Ncf=0,1 時，則待識別信號為非FSK 的其它調(diào)制樣式信號。

圖3、圖4 和圖5 說明了在待識別循環(huán)頻率α′處的2FSK 信號循環(huán)矩幅度估計量分別在SNR=10 dB、0 dB、-5 dB 的取值。

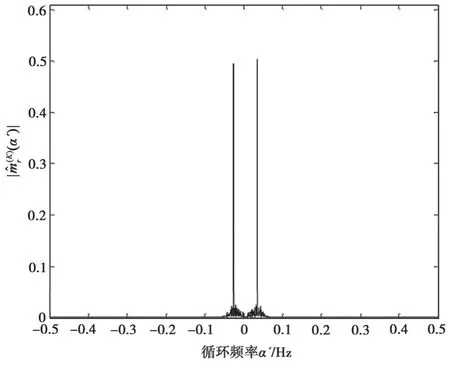
圖3 信噪比為10 dB 時2FSK 循環(huán)矩幅度估計量

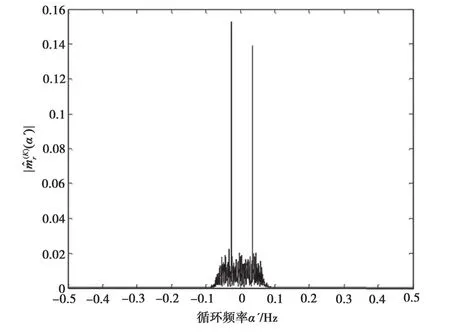
圖4 信噪比為0 dB 時2FSK 循環(huán)矩幅度估計量

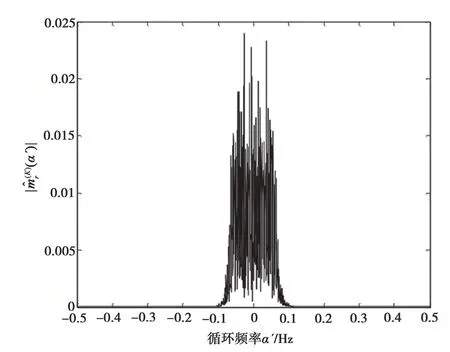
圖5 信噪比為-5 dB 時2FSK 循環(huán)矩幅度估計量

可見，當(dāng)SNR=10 dB 時，循環(huán)頻率α 處的循環(huán)矩幅度估計峰值約為0.5。α′=α 處的峰值隨著信噪比的減小而變小。

3 仿真結(jié)果及性能分析

對本文改進(jìn)的識別方法有效性開展驗(yàn)證，開展了以下仿真試驗(yàn)。設(shè)信號采樣率為200 MHz，信號載波頻率為60 MHz，Monte-Carlo 仿真次數(shù)為1 000次。采取改進(jìn)思路對目標(biāo)信號盲識別，得出了識別正確率。其仿真結(jié)果如圖6 所示，其中橫軸代表信噪比SNR，單位為dB，縱軸代表正確識別率，不同形狀的曲線表示不同進(jìn)制階數(shù)的FSK 信號。

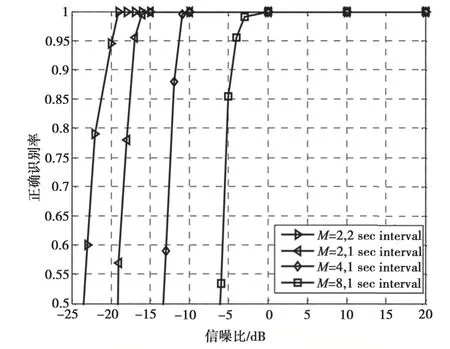
圖6 新方法對不同進(jìn)制數(shù)和觀測間隔FSK 信號識別率曲線

圖6 顯示了使用該方法實(shí)現(xiàn)的分類性能。對于高階調(diào)制，要達(dá)到一定的分類性能，需要較高的信噪比。例如，2FSK、4FSK 和8FSK 信號達(dá)到正確識別概率為90%時分別須要-17.31 dB、-11.82 dB和-4.56 dB 的信噪比。并且，樣本觀測間隔（interval）越大也即信號樣本周期的點(diǎn)數(shù)越多，根據(jù)循環(huán)矩估計量得到的判斷則越準(zhǔn)確，分類性能越好。對于2FSK 信號觀測間隔等于2 s 的情況相比間隔等于1秒的情況，識別正確率達(dá)到90%時所需的信噪比相對更小。并且對傳統(tǒng)的調(diào)制識別方法和本文中新改進(jìn)識別方法進(jìn)行性能仿真比較，橫軸表示信噪比，縱軸表示FSK 信號調(diào)制識別率，如圖7 所示。

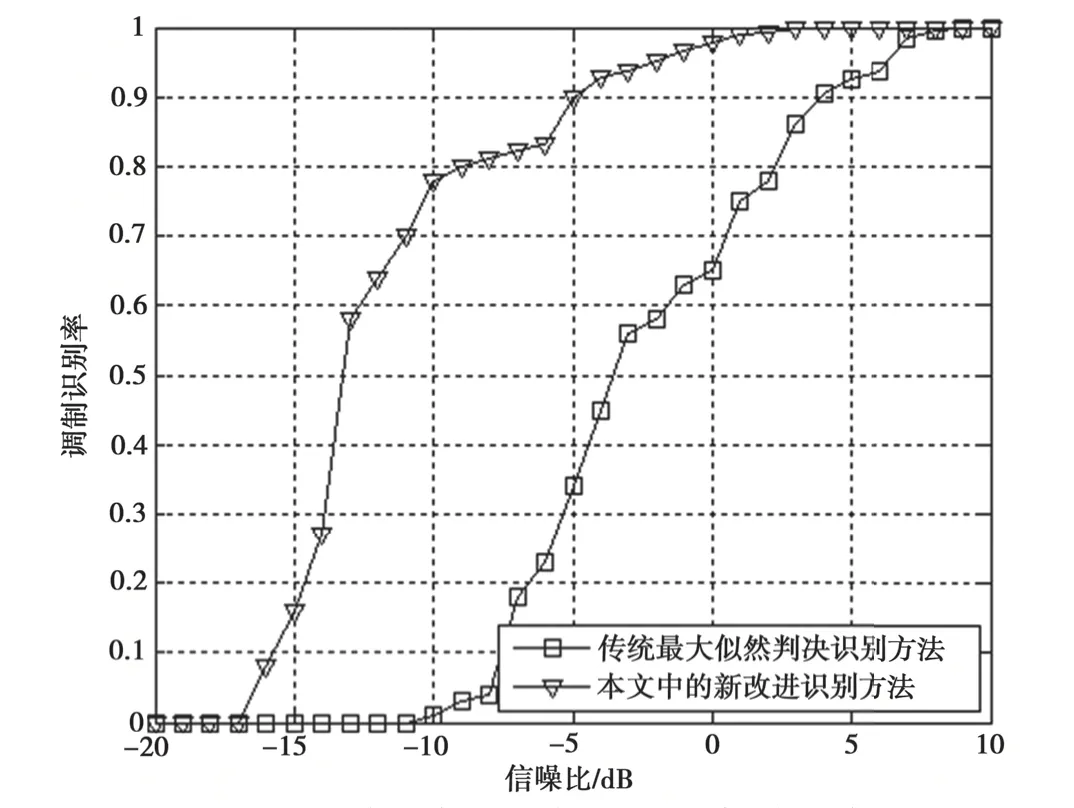
圖7 改進(jìn)方法與過去方法的識別性能比較

由圖7 可以看出，新改進(jìn)識別方法比起傳統(tǒng)的調(diào)制識別方法具有相對更優(yōu)的性能，也適用于較低信噪比環(huán)境條件下對FSK 調(diào)制信號的處理。

4 結(jié) 語

隨著電磁環(huán)境的日益復(fù)雜與認(rèn)知無線電技術(shù)的不斷發(fā)展，信號盲識別處理的研究越來越受到重視。本文通過對頻移鍵控信號模型深入地進(jìn)行分析，提出了一種基于循環(huán)平穩(wěn)特性的FSK 信號盲識別算法，該算法無需任何先驗(yàn)條件，也不依賴于載波和定時恢復(fù)等預(yù)處理，具有良好分類性能，識別正確率優(yōu)于過去一些方法。今后將進(jìn)一步擴(kuò)展優(yōu)化，為解決非協(xié)作信號的分析和處理提供更有效的手段，并為網(wǎng)電空間監(jiān)測與智能信號處理領(lǐng)域的研究貢獻(xiàn)力量。