守正考綱 著眼能力 彰顯素養
——2019年高考全國理綜Ⅰ卷第21題評析與教學思考

許冬保

(九江第一中學,江西 九江 332000)

1 原題再現

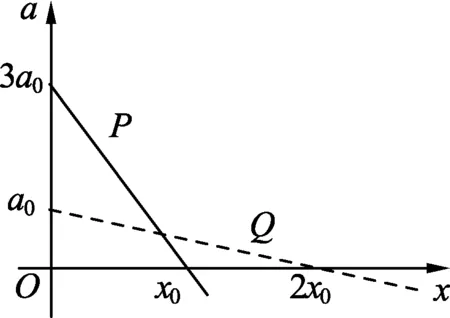
圖1 a-x圖像

題目.(2019年全國理綜Ⅰ卷第21題)在星球M上將一輕彈簧豎直固定在水平桌面上,把物體P輕放在彈簧上端,P由靜止向下運動,物體的加速度a與彈簧的壓縮量x間的關系如圖1中實線所示.在另一星球N上用完全相同的彈簧,改用物體Q完成同樣的過程,其a-x關系如圖1中虛線所示,假設兩星球均為質量均勻分布的球體.已知星球M的半徑是星球N的3倍,則

(A)M與N的密度相等.

(B)Q的質量是P的3倍.

(C)Q下落過程中的最大動能是P的4倍.

(D)Q下落過程中彈簧的最大壓縮量是P的4倍.

2 試題解析

解法1：物體剛放在彈簧上端時,彈簧彈力為零,圖2(甲)所示,物體的加速度為重力加速度.由牛頓運動定律,有

mg-kx=ma.

可見,隨著物體向下運動,彈簧的形變量不斷增大,物體做加速度不斷減小、速度不斷增大的變加速運動.當加速度為0時,速度有最大值,圖2(乙)所示.此后,由于慣性物體繼續向下運動,加速度不斷增大且方向向上,物體做減速運動,直到速度減到0,圖2(丙)所示,此后物體來回做往復運動.

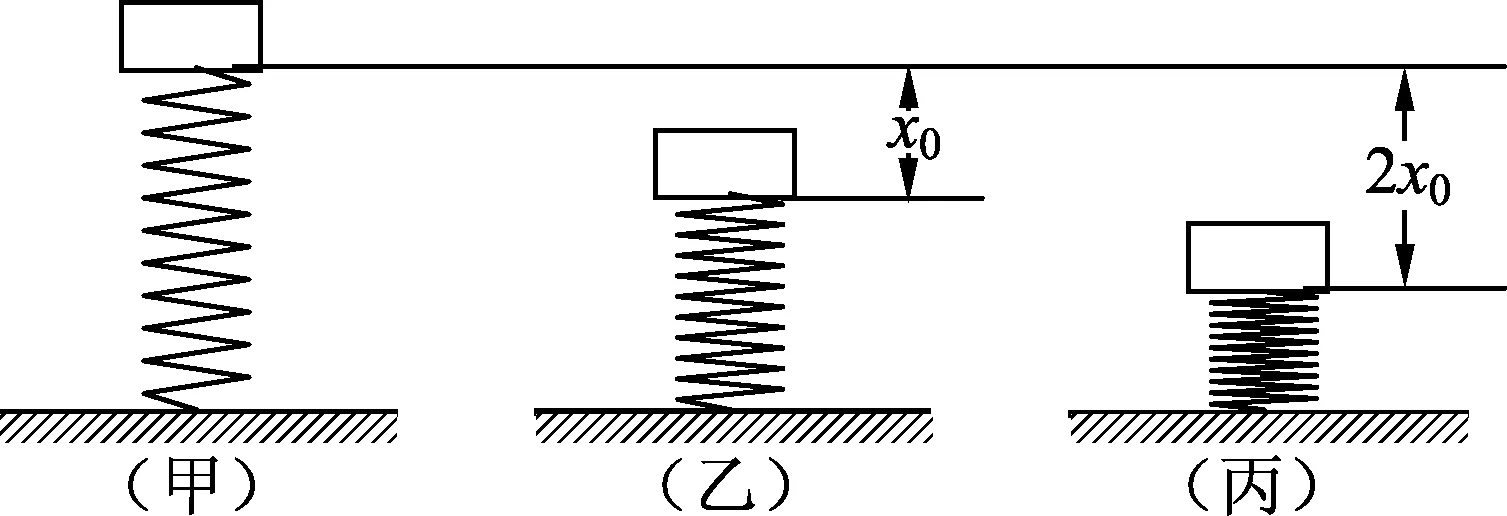
圖2 物體P壓縮彈簧的過程分析

在圖1中,物體P、Q的最大加速度分別等于星球表面的重力加速度,即在星球M表面的重力加速度大小為星球N的3倍.

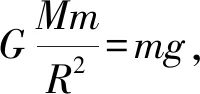
由圖1知,物體的加速度為0時,物體P、Q作用下彈簧的壓縮量分別為x0，2x0.若x0對應的彈簧彈性勢能為Ep,則物體P、Q作用下相應的彈簧彈性勢能分別為Ep、4Ep.物體P作用下,對于彈簧與物體P所組成的系統,在由靜止釋放至平衡位置(即最大速度)的過程中,由機械能守恒定律,有

mP·3a0·x0=EkP+Ep.

mQ·a0·2x0=EkQ+4Ep.

式中EkP、EkQ分別為P、Q的最大動能.

由于mQ=6mP,解得EkQ=4EkP,選項(C)正確.

對于物體與彈簧所組成的系統,在物體由靜止釋放至壓縮量達最大值xm的過程中,由機械能守恒定律,有

綜上分析,該題正確選項是(A)、(C).

解法2：僅對選項(C)、(D)給出另類解法.

物體輕放在彈簧上端由靜止向下運動,物體壓縮彈簧,該過程物體做加速度不斷減小的加速運動,隨后,做加速度不斷增大的減速運動,而后又向上運動,如此往復運動,即機械振動中的簡諧運動.

圖3 P的a-x圖像分析

研究物體P的運動.如圖3所示,考察圖1中圖線與橫軸所圍成的“面積”,若該“面積”乘以物體的質量,所得結果表示合外力所做的功.因此,物體的最大動能可以用圖3上部分圖象的“面積”與質量的乘積來計算.

設物體P、Q的最大動能分別為EkP、EkQ,則由動能定理,有

根據解法1中的結果mQ=6mP,因此,EkQ=4EkP,結果同上.

由圖3還可以得到:物體P向下運動的速度減為0時,對應的加速度及壓縮量分別為-3a0，2x0,因此最大壓縮量為2x0.同理,物體Q壓縮彈簧,最大壓縮量為4x0.

關于最大壓縮量的分析,還有一種更為簡單的方法來判斷.由于簡諧運動具有時間、空間的對稱性,因此,物體P、Q在下落中彈簧的最大壓縮量分別為2x0、4x0,即Q下落過程中彈簧的最大壓縮量是P的2倍,所得結果同上.

3 試題評價

物理學科核心素養是學生通過物理學習形成的關鍵能力和必備品格[1].核心素養理念下的命題,凸顯知識、能力與科學素養的考查.通過命題導向引導中學教學從“解題”向“問題解決”轉變,強化綜合能力和創新思維的考查,[2]以此促進物理學科核心素養的發展.試題評價堅持得、失兩方面考量.

3.1 守正考綱,突出基礎性與綜合性的考查

解法1是受傳統思維影響下的一種經典解法,思路中規中矩.由于涉及彈簧彈性勢能的表達式,因此,試題的出現立即引發了廣大一線教師的爭議,認為彈簧彈性勢能的考查具有超綱[2，3]之嫌.然而解法2,直接回避了彈簧彈性勢能的表達式,且解法簡潔明了,以物理科學方法(微積分思想方法、轉化方法、對稱性方法)的考查化解了“超綱”嫌疑,良苦用心,令人拍手叫絕.

試題以物體與彈簧的相互作用為載體,依托a-x圖像,呈現相關信息.要求能綜合萬有引力定律、牛頓運動定律、胡克定律、動能定理等力學中的重要規律來解決問題;涉及到星球的均勻球體模型、彈簧振子及其簡諧運動的理想化模型;此外,試題解答中涉及較多的研究對象,如星球M與N、物體P與Q、物體P及Q與彈簧構成的系統.眾多信息的分類、提取與處理,使試題具有較高的區分度.

3.2 著眼能力,落實科學思維能力的考查

高考作為選拔性考試,能力的考查置于首要位置.試題考查了引力、重力、加速度、形變、密度、動能、功等物理學中的核心概念,考查了幾乎涵蓋全部力學規律的運用.作為壓軸選擇題,試題力求通過知識的理解及其運用來鑒別考生能力的高低,所考查的能力主要有:理解能力、信息處理能力、推理能力、分析綜合能力.

此外,試題非常重視對圖像的考查.a-x圖像中的橫軸截距、縱軸截距、圖線與橫軸所圍成的“面積”等信息所對應的物理意義的理解與應用,體現了應用數學處理物理問題能力的考查.通過圖像“面積”與物體質量的乘積來計算物體的最大動能、通過對稱性方法(圖像對稱或運動對稱)的應用來確定彈簧最大壓縮量等,對考生發散思維能力及創新思維能力進行了一定層次的考查.

3.3 彰顯素養,關注物理核心素養的考查

高考物理試題著重考查考生的知識、能力和科學素養.物理學科核心素養是科學素養的重要組成部分.學科核心素養是學科育人價值的體現,是學生通過學科學習而逐步形成的正確價值觀念、必備品格和關鍵能力.

試題考查了引力場的物質、運動與相互作用以及能量等重要物理觀念;考查了模型構建、科學推理等科學思維能力;考查了基于a-x圖像探究物理規律的方法;考查了綜合運用所學規律,根據情境,加工信息、縝密推理,追求科學本質的態度.在試題設計中,巧妙地根據圖像“面積”,通過考查科學方法的應用來規避彈簧的彈性勢能的定量表達式,體現了命題設計者嫻熟的命題技能.要求考生具有較強的洞察力和發散的思維能力.關于應用對稱性判斷物體壓縮彈簧的最大壓縮量,要求考生結合圖像“面積”的意義,通過延伸圖線,繪出圖3所示的圖像進行直觀分析,得出結論.或者根據簡諧運動模型,從運動的整體上來思考問題,從而獲得空間位移對稱性的重要特征.綜上分析,試題較好地考查了考生的物理學科核心素養.

3.4 簡諧運動模型的引入,一定程度上挑戰考試的公平性

物體與彈簧所構成的系統的運動即為簡諧運動.但是,簡諧運動是選考模塊3-4中的內容,對于只學習模塊3-3的考生,關于物體的運動分析則增加思維的難度,特別是彈簧最大壓縮量的分析,考生很難從運動對稱性的角度來進行思考.而對于學習模塊3-4的考生,關于該運動模型的分析可謂“輕車熟路”.基于此,該題對于部分考生有失公平性.

3.5 彈性勢能表達式的介入,可能會引發超綱教學與超綱訓練

考試大綱關于“彈性勢能”只字未提.考慮到機械能中包含彈性勢能,因此,關于彈簧彈性勢能的教學,多年來遵循一個潛規則:知道彈性勢能的概念,定性掌握彈簧彈性勢能與勁度系數、形變量有關,或知道其數學表達式,但不要求用表達式來定量求解有關問題.

如上所述,試題沒有超綱.但是,解法1表明,在已知彈簧彈性勢能表達式的前提下,雖然通過比較麻煩的方法,但還是得到了正確答案.這種解法在認知心理學中屬于弱方法,且思維品質較低.如果以分數論,這種以犧牲時間、精力為代價的勞動在某種意義上是值得的.高考試題對教學的導向性是不容低估的.在應試背景下,可能會導致中學物理的超綱教學與超綱訓練.因此,在追求分數的理念下,試題為超綱教學與超綱訓練帶來了“借口”,難免會由此而增加學生的學習負擔.

4 教學思考

4.1 重視模型教學,發展科學思維能力

科學思維是對客觀世界本質屬性、科學規律的認識方式,是基于經驗事實建構物理模型的抽象與概括過程,是分析綜合、推理論證等科學方法在問題解決中的具體應用.

科學思維作為重要的科學素養,高考試題關于科學思維的考查,主要包括能否將實際問題中的對象和過程轉化成物理模型;能否對綜合性物理問題進行分析和推理,獲得結論并作出解釋;能否采用不同方式分析解決物理問題.[4]試題分析中對于物體與彈簧構成的系統及其往復運動模型的建構、定性分析、定量分析等的綜合應用,是試題解答中科學思維能力的集中表現,通過試題解答能較好地甄別考生科學思維發展的水平.

發展學生的科學思維能力是重要的教學目標之一.建構模型是一種重要的科學思維方法.靈活地建構物理模型來解決問題是解題中不可缺少的認知與能力.在高中物理教學中,共涉及到5類典型的運動模型,即勻速直線運動模型、勻變速直線運動模型、勻速圓周運動模型、拋體運動模型、簡諧運動模型等.教學中要求能對各類模型的建構、拓展、應用進行梳理,通過梳理讓學生體會建構模型的思維方法,理解物理模型的適用條件,掌握應用模型解決具體問題的思維方法,促進科學思維能力的發展和提升.

4.2 依據考綱教學,重視科學方法教育

考試大綱是命題的規范性文件與標準,也是考試評價與復習備考的依據.多年來高考試題堅持不超綱命題,但考綱邊緣或綱外知識點,如彈簧的彈性勢能、引力勢能、流量概念等在高考試題中頻頻出現.對于新的知識點,試題可能給出文字信息或表達式,以已知條件來呈現有關綱外知識內容;也可能是通過物理科學方法來考查綱外有關知識.彈簧的彈性勢能不是考綱規定的內容,但若通過有關科學方法來考查彈性勢能的問題則不屬于超綱命題.如借助于彈簧彈力與彈簧形變量的關系圖像,通過圖線下方的“面積”來求彈簧彈力功(或彈性勢能)的方法的考查屬于能力考查的層次.在人教版物理必修2[5]中,有一節內容是探究彈性勢能的表達式,而探究的方法是微積分思想方法或微元法的應用.

物理學家費恩曼認為,科學的核心或者說全部就是科學方法.換句話說,科學方法比科學知識更重要.已有研究表明:方法是通向能力的橋梁,能力既依賴于知識,更依賴于方法.在某種意義上,方法本身是能力的一部分.[6]因此,科學方法的教育是與概念、規律教學同等重要的教學目標和教學內容.

如上所述,不要因為涉及彈簧彈性勢能的定量表達式,就進行大規模的超綱教學與超綱訓練,當然適度的超綱是無可非議的.以物理科學方法的隱性滲透或顯化教學,來解決所謂的超綱問題,符合課程理念和時代要求.

4.3 關注選考模塊,全面提高學科素養

試題以彈簧振子做簡諧運動的模型為情景立意設問,創新命題思路可圈可點.對于最大形變量的分析,若依簡諧運動模型進行對稱性方法分析,問題解答既簡潔快捷又提升思維品質.在必考試題中,考查選考知識內容.從學科素養的發展和提高的角度來認識,這一命題導向具有積極的意義,對教學的影響是巨大的.

物理選考模塊有3-3及3-4.由于多方面因素的影響,時下多數學校只安排一個模塊的教學.單一模塊的教學造成的后果主要有三:首先,模塊的選擇由學校統一安排,并未考慮學生的興趣、愛好,剝奪了學生自主選擇模塊學習的權利;其次,導致高中物理知識結構缺乏系統性,學生知識結構的斷裂,對于學生跨入高校的進一步學習帶來障礙,直接影響學生學科素養的發展;最后,由于高校自主招生的命題不受考綱約束,模塊3-3及3-4均在考試命題范圍之列,單一模塊的教學直接影響參與自主招生考試學生的測試結果.因此,同時進行兩個模塊的教學,有利于學生的個性發展,有利于學生知識結構的完善及學科素養的全面提升.

如果能在必考模塊中,適當增加選考內容,使得沒有系統學習相關選考模塊內容的考生在分析時帶來困難,而使得已經系統學習相關選考模塊內容的考生輕松解答.這對于選考模塊的教學導向具有十分重要的指導意義.