基于時差收斂算法的聲發射源定位方法
張延兵,宋高峰,朱 峰
(1.江蘇省特種設備安全監督檢驗研究院南通分院, 南通 226011;2.東南大學 機械工程學院, 南京 211189)
基于聲發射(AE)信號到達時差的定位計算是聲發射檢測中最為常用的定位方法,其主要原理為將聲發射信號超過信號采集門檻值時聲發射信號到達傳感器的時刻作為參與定位計算的起始時刻,進而獲取聲發射源的準確位置坐標[1]。此種定位方法,在傳感器信噪比較低、聲發射信號在介質中的距離衰減、實際構件中不同方向聲波傳輸速率的差異、結構不連續帶來的波形畸變等諸多因素的綜合作用下,數據采集門檻設定值與檢測儀器靈敏度間會出現不匹配而引起較大的定位誤差。針對上述問題,筆者嘗試采用一種基于收斂算法的AE源定位方法,通過對基于聲發射信號到達時刻的定位結果進行循環迭代計算,使得可以參與某聲發射事件定位計算的各定位組重構的位置坐標,越來越接近收斂于同一點(或區域),并最終實現理想精度的定位結果。
1 延時對算法定位精度的影響
傳統的聲發射激勵響應時間測量方法主要采用門檻分析法[2-3],即根據材料的塑形特性、現場檢測環境(如噪聲)、檢測儀器配置、加載方式等因素綜合選取檢測門檻值,最終將傳感器獲取的信號第一次超過門檻的時間,作為AE信號首次被接收的時刻,并據此計算各通道采集到的聲發射信號到達時差。在實際的計算過程中,閾值電平的設置會直接影響到最終聲發射源定位結果的精度。為分析此問題,以聲發射中較為直觀的線定位試驗進行論證分析,將傳感器S1、S2相距100 mm成直線布置,并在兩個傳感器之間的P點進行激勵,P點與S1距離為70 mm。
圖1和圖2為S1、S2采集到的聲發射信號波形,分別記為x1和x2。根據實驗室環境及試件材料選取檢測門檻值為0.019 96 V,此時兩個傳感器測得的信號到達時差為9μs;當調整檢測門檻值為0.034 0 V時,兩個傳感器測得的信號到達時差為11μs。依據上述數據計算信號源的位置,所得的定位結果如表1所示。

圖1 聲發射波形圖(門檻值為0.019 95 V)
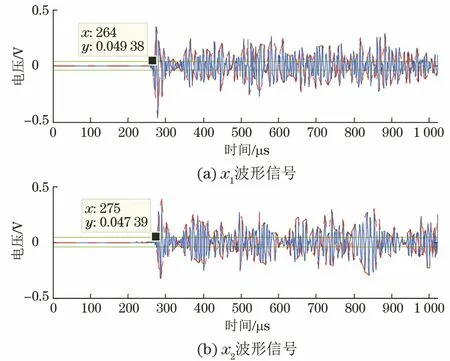
圖2 聲發射波形圖(門檻值為0.033 9 V)

表1 聲發射線定位結果分析
從表1可見,信號采集門檻的差異,導致定位源位置出現了較大的偏差,相對于定位組最遠兩個傳感器間距100 mm,其比例已近7.5%,這顯然不符合NB/T 47013.9-2015 《承壓設備無損檢測 第9部分 聲發射檢測》中5%的要求。通過以上分析可知,采集門檻的選擇稍微有所不同都會導致定位精度的較大偏差,而采集門檻的選擇受到諸多因素影響,例如:傳感器所處位置的環境噪聲、結構類型、距離加載位置的遠近等,在實際的檢測中不可避免會選擇適宜的信號采集門檻閾值,而這些微秒級別的誤差,也會大大影響定位的精度。
為解決門檻閾值差異對于傳感器時差獲取的影響,也可以采用互相關算法[4],其主要的原理為:對于相同的聲發射事件,無論被多少個傳感器接收,其信號在特性上具有很強的匹配程度,唯有信號在傳播時會出現不同程度的衰減或信號模式變化,因此可以通過對其在時域內進行互相關計算,以確定信號相對于不同采集通道的到達時間,進而計算聲發射源的精確位置。此種方法在細長型結構中的應用效果較好,但在面積結構、大型體積型結構,尤其是復雜結構件中,結構的不連續和材料的各項異性會使得聲發射信號在傳播過程中產生大量反射、散射、波形畸變與疊加效應等,信號特征相較于原始波形也就產生非常大的差異,此時簡單通過相關計算時差的方法就失去了作用。對于此問題也有通過經驗模態分解、小波分析[5]等方法提取有效聲源信號的缺陷特征頻段進行重構后,再進行互相關分析獲取時差,從而提高聲發射源定位精度計算結果的有效性[6],但實際的工程應用效果還不是很理想。
2 收斂算法的聲發射源定位方法

為測試收斂算法的聲發射源定位方法,選取4個傳感器進行試驗,分別記為S1,S2,S3和S4,在某一區域進行一個信號激勵,假定S2,S4,S3號傳感器相對于S1號傳感器的時差為T(Δt1,Δt2,Δt3)。將4個傳感器中每任意3個作為一個定位組,得到4組定位數據,其編組信息如表2所示。

表2 傳感器編組信息


圖3 聲發射源定位點區域圖
進而,可通過此次試驗結果中4組定位的中心位置L反求出理想定位目標點的時差T′(Δ1,Δ2,Δ3),如式(1)所示。
Δ1=(R2-R1)/v
(1)
式中:R1、R2、R3、R4為目標中心點L到每個傳感器的距離(見圖4);v為波速。

圖4 聲發射傳感器布置圖
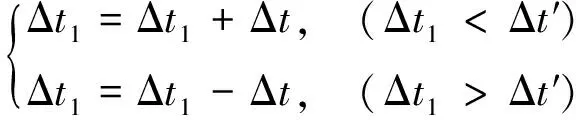
(2)
式中:Δt為修正步長,一般為0.050.5μs。
以此可類推修正Δt2,Δt3的值,最后依據修正后的Δt1,Δt2,Δt3,用三角定位算法重新計算,得到新的4組聲發射源定位L1,L2,L3和L4。重復上述步驟,直至四邊形L1L2L3L4越來越收斂,最終接近于同一個區域。在此計算過程中,以四邊形L1L2L3L4的邊長和作為優化目標函數進行計算,即:
F(T)=d(L1,L2)+d(L2,L3)+
d(L3,L4)+d(L1,L4)
(3)
式中:d(L1,L2)為L1與L2之間的距離;d(L2,L3)、d(L3,L4)和d(L1,L4)分別為L2與L3,L3與L4,L1與L4之間的距離。
通過循環迭代計算,使F(T)函數漸趨收斂直至穩定,此時即可認為該算法在多定位組條件下重構的聲發射源位置坐標最為理想且誤差最小。算法的具體流程如圖5所示。
3 斷鉛試驗及分析
3.1 試驗過程
為了從試驗角度驗證基于收斂算法的AE源定位方法的準確性,設計制造了一塊正方形鋼試板進行測試,傳感器位置陣列如圖6(a)所示,其坐標(單位為mm,下同)分別為(0,0),(140,0),(140,140)和(0,140)。各采集通道靈敏度測試結果顯示響應靈敏度在±4 dB之間,傳感器耦合性能良好。首先在試板上進行4次斷鉛試驗,坐標分別為(40,40),(40,100),(100,100)和(100,40),每個點測試5次。

圖6 聲發射源定位試驗傳感器布置
3.2 試驗結果分析

圖7 3種方法的聲發射源定位圖
使用美國物理聲學公司PAC的AEWin聲發射采集系統進行試驗,并對獲取到的聲發射檢測數據進行解析處理,得到各通道采集到的聲發射信號及相應的到達時間及定位數據。為驗證新的定位算法的準確性以及其相對于傳統時差定位的優勢,試驗通過收斂算法的聲發射源定位算法對此次檢測數據進行重構迭代計算,以形成新的定位源位置,從而與原有時差計算的位置進行比對。選擇4組傳感器進行定位測試,對于同一聲發射源事件,每任意3組傳感器均可進行獨立的定位計算,將試驗定位結果與最小平方法聲發射源定位以及基于時差收斂算法計算的結果等三者進行對比。表3為AEWin系統定位結果,表4為最小平方法定位計算結果,表5為基于收斂算法的定位計算結果。圖7為3種方法的聲發射源定位圖。

表3 AEWin聲發射源定位結果 mm

表4 最小平方法聲發射源定位結果 mm

表5 基于收斂算法的聲發射源定位結果 mm
由圖7可以看出,基于收斂算法的聲發射源定位方法獲取的定位事件的集中度更好,而其他方法由于定位精度的差異,定位事件的離散度較高;另一方面,從定位誤差(見表6)的均值和方差(與實際模擬聲發射源的真實位置進行對比)也可以看出,基于收斂算法的源定位位置偏差明顯小于其他兩種方法的。而在實際的檢測環境中,設備的尺寸和結構相對于試驗試板的幾何參數更大,型式更復雜,必然導致時差獲取的誤差大大增加,進而嚴重影響定位的精度。

表6 3種方法定位誤差結果比較
4 結語
針對傳統聲發射定位計算方法的不足導致定位精度下降的問題,提出了一種基于收斂算法的聲發射源定位方法,并通過理論分析和試驗測試,驗證了該定位算法在解決多定位組過定位、復雜結構、信號畸變、采集門檻差異、信號距離衰減等問題時,比傳統時差定位具有更好的定位精度和定位源位置收斂的穩定性。

