沖擊荷載作用下地基土變形及動力特性

王俊林, 許 琨

(1.鄭州大學水利與環境學院，鄭州 450001；2.機械工業第六設計研究院有限公司，鄭州 450007)

分布在中國中西部地區的黃土大多具有濕陷性，濕陷性黃土遇水后會強度降低，原狀土體顆粒重新排列，出現大幅度沉降變形等現象，對周邊構筑物造成一定危害。目前對濕陷性黃土處理的方法有強夯法、預浸水法、換填法等，強夯法因造價低、施工方便等原因被廣泛應用。

許多學者對強夯加固機理進行了研究，Leon[1]、吳銘炳等[2]、左名麒[3]采用三角形荷載，通過波動理論對強夯加固地基機理進行了分析。田水等[4]通過大變形數值根據強夯過程中土體密度的變化分析了加固深度的影響因素。賈敏才等[5]通過室內試驗和數值計算分析了土體顆粒在強夯過程中的運動規律，闡釋了強夯動力特性。姚占勇等[6]采用施加初速度方式模擬真實動力沖擊荷載，對強夯過程中土體應力-應變特征和加固范圍發展規律進行了研究。羅啟添[7]基于現場實測結果對強夯震動衰減規律進行研究，明確在施工過程中需要設置安全距離。夏東超等[8]、韓云山等[9]從動力學角度分析夯錘的沖擊行程，探索了表征夯錘沖擊效能的方法，為優化強夯設計提供參考。

在ABAQUS框架內，應用Mohr-Coulomb模型、施加剛體沖擊荷載、非線性大變形有限元算法及ALE自適應技術，對變形、應力和加速度進行系統研究。結合現場試驗驗證計算模型合理性，研究了不同能級、不同沖擊次數、不同土體彈模對地基土體變形、應力、速度及加速度的影響。對沖擊荷載作用下土體變形規律、能量傳遞規律等進一步分析，為今后強夯加固機理研究和設計施工提供理論支持。

1 分析模型建立

1.1 本構模型

采用能夠很好地模擬沖擊荷載的Mohr-Coulomb本構模型(圖1)，且計算過程中不考慮孔隙水壓力。

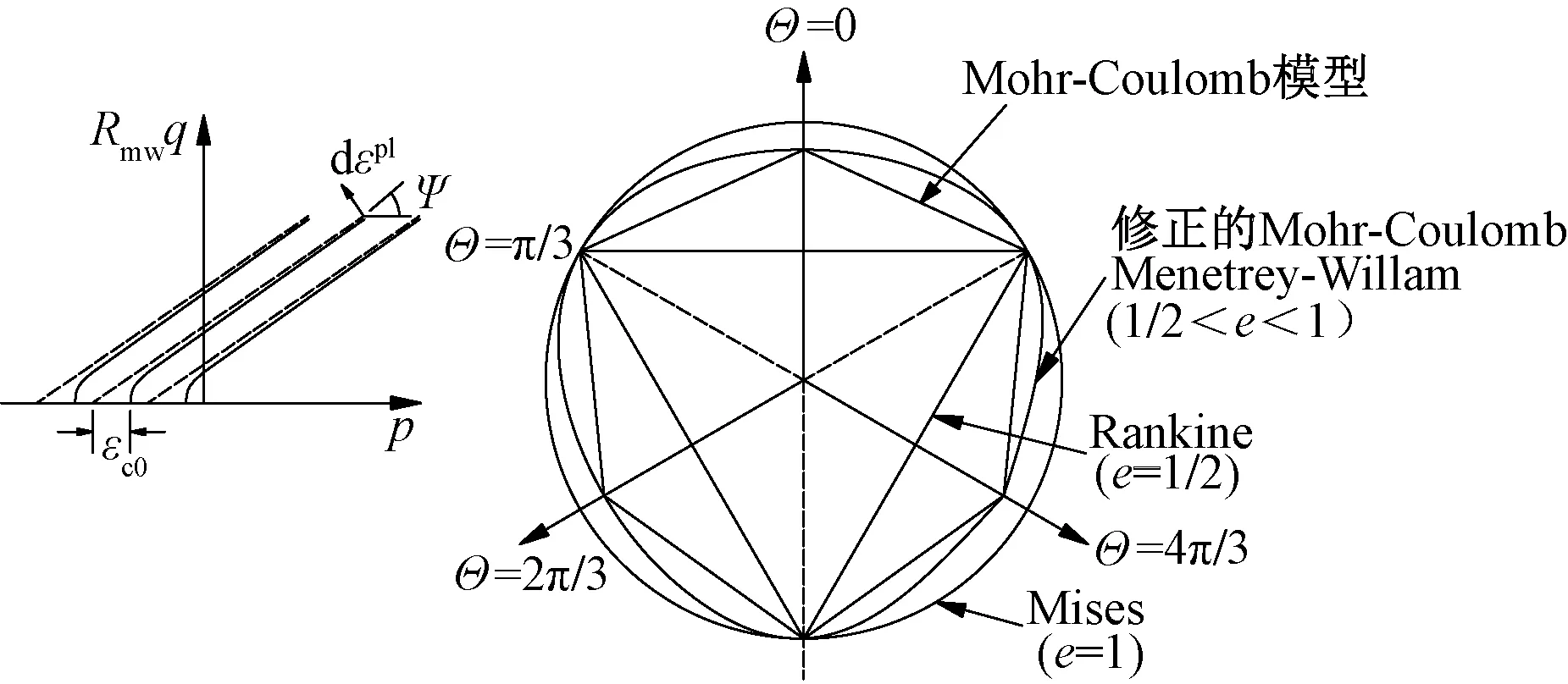
Ψ為膨脹角；ε為子午面上的偏心率；e為π面上的偏心率；Θ為極偏角

1.2 土體參數

洛陽市某中學地基處理工程，位于澗河旁沖積二級階地，場地較平整，根據勘察結果，原狀地面以下7 m深范圍，黃土有濕陷性。通過現場試驗測得的應用于模型計算所需土體各項物理力學性質指標如表1所示。

表1 強夯計算所需參數

錢家歡等[10]指出在沖擊荷載作用下，土體彈性模量E=E0N0.516，其中，E0為初始彈模；N為夯擊次數；E為N次夯擊后土體彈模。在計算過程中所需參數參照文獻[11]計算公式，如式(1)所示：

(1)

式(1)中：E為彈性模量；Es為壓縮模量；μ為泊松比。

(2)

式(2)中：G為剪切模量。

(3)

式(3)中：cc為縱波的傳播速度；ρ為材料密度。

(4)

式(4)中：cs為橫波的傳播速度。

波的傳播頻率，假設f=10 Hz，波長L=c/f≈ 9.4 m。

1.3 荷載與邊界條件

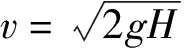
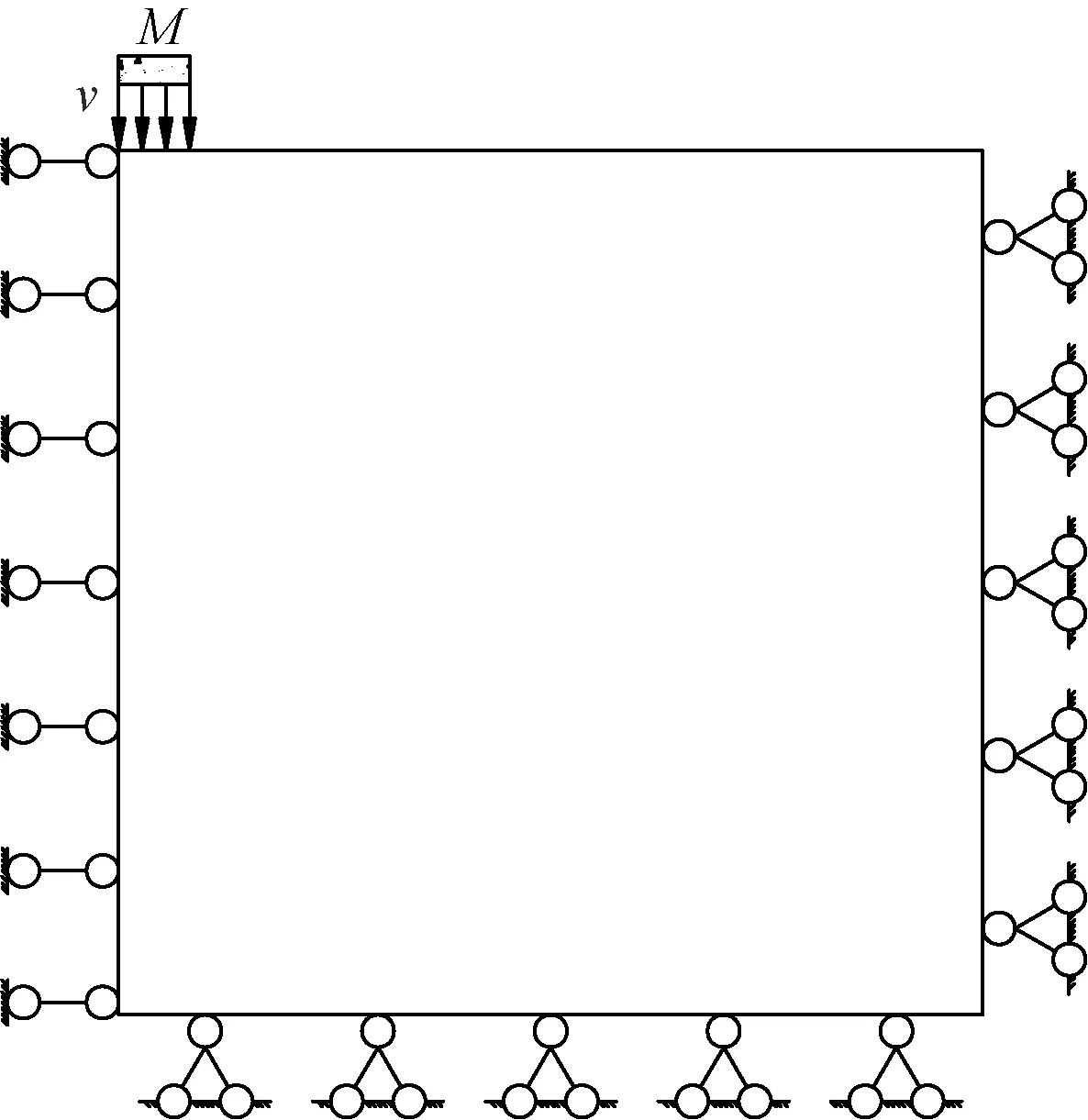
M為夯錘重量

為較少計算過程中沖擊波在邊界產生反射而影響計算精度，采取黏性邊界條件，同時在計算時考慮阻尼效應。

1.4 單元選擇和網格的處理

劉毓氚等[13]發現在模擬爆炸或沖擊荷載時，一節單元效果更好，所以采取一階線性4節點單元。計算采用軸對稱模型，網格采用每波長10個節點，時間步Δt不大于Δx/c(Δx為網格增量；c為波速)。

2 強夯特性計算結果分析

2.1 模型合理性驗證

圖3所示為夯擊能2 000 kN·m、不同夯擊次數作用下夯沉量。通過將計算結果和現場實測夯沉量對比，發現計算結果和實測夯沉量較為相似，說明計算模型具有可行性。

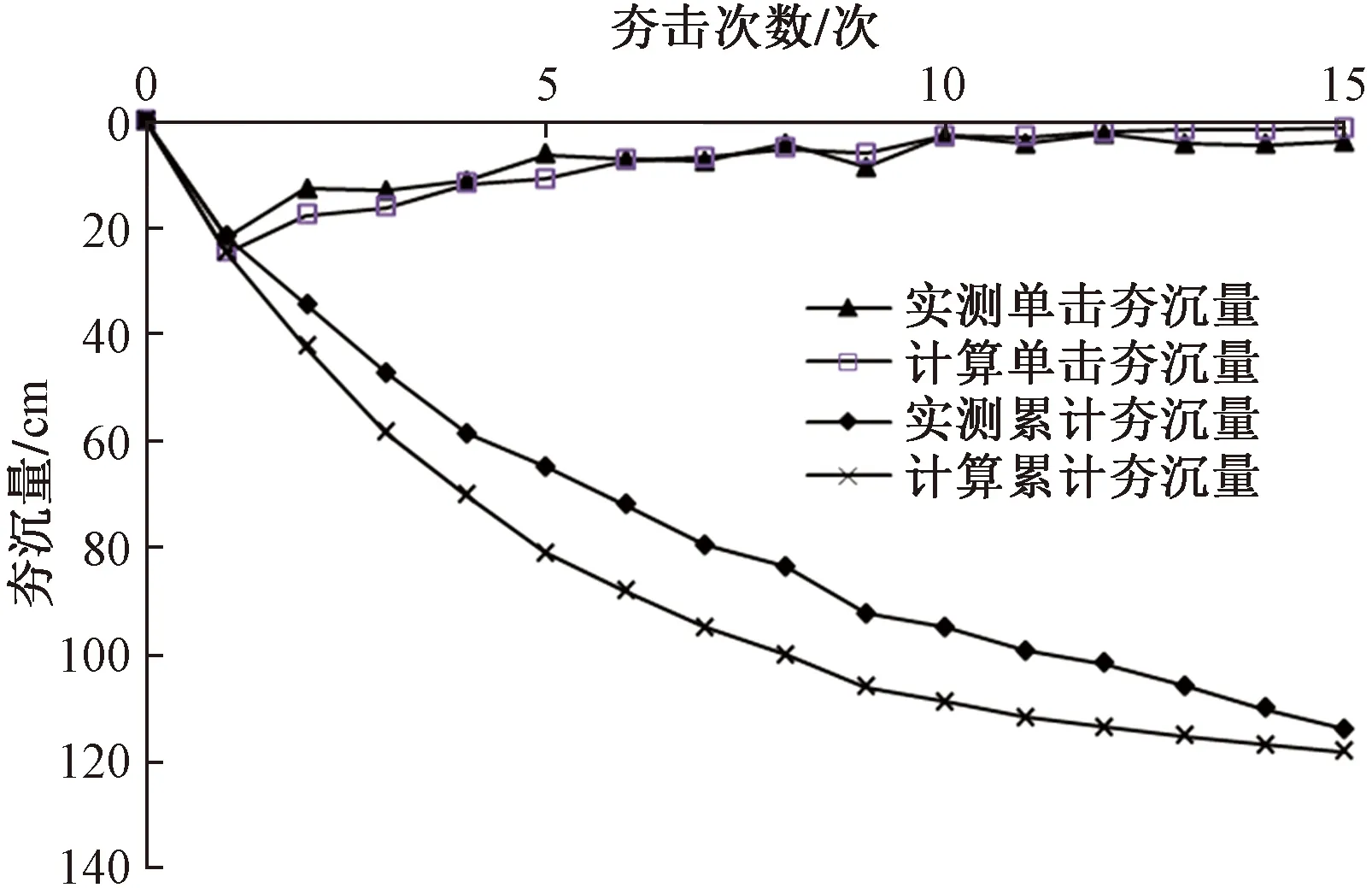
圖3 計算結果與實測夯沉量比較

2.2 強夯變形特性計算結果分析

圖4所示為沖擊荷載下不同深度變形，錘體中心下方沉降和周邊隆起高度隨深度的增加而減小，錘體中心線周邊2～5 m出現不同程度隆起，說明錘體向下沖擊壓縮錘下土體的同時也對周邊土體產生一定的側擠，也會造成周邊表層土體出現松散現象。

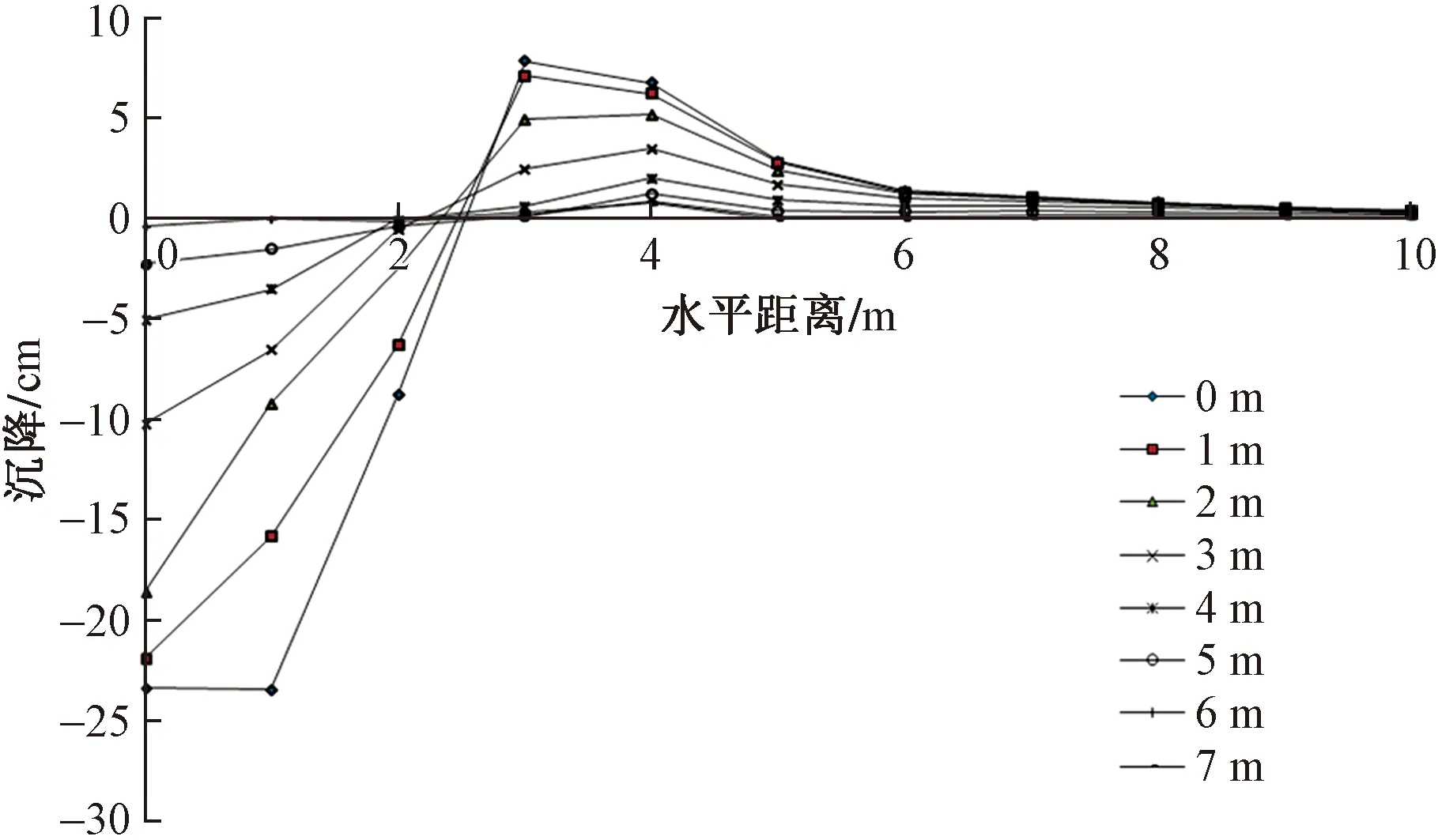
圖4 沖擊荷載作用下不同深度沉降變形

圖5所示為在不同能級沖擊荷載作用下，錘下土體沉降量與周邊隆起量隨夯擊能增加呈線性增長狀態：y=0.009 2x+7.467 3(x為夯擊能；y為沉降量)，y=0.003 5x+1.356 2(x為夯擊能；y為隆起量)，說明沖擊能量越大，錘下土體壓縮量和周邊側擠隆起量越，影響范圍也就越大。圖6表明在2 000 kN·m沖擊能量作用下，當彈模E>10 MPa時，錘下土體沉降量與土體彈性模量為線性關系：y=-0.116 6x+25.296(x為彈性模量；y為沉降量)，隆起高度隨彈模增大而漸小且逐步趨于平穩，說明彈模較大時土體在沖擊荷載作用下塑性變形愈發不明顯，而彈模E<10 MPa時，土體在錘體沖剪作用下主要產生塑性變形。

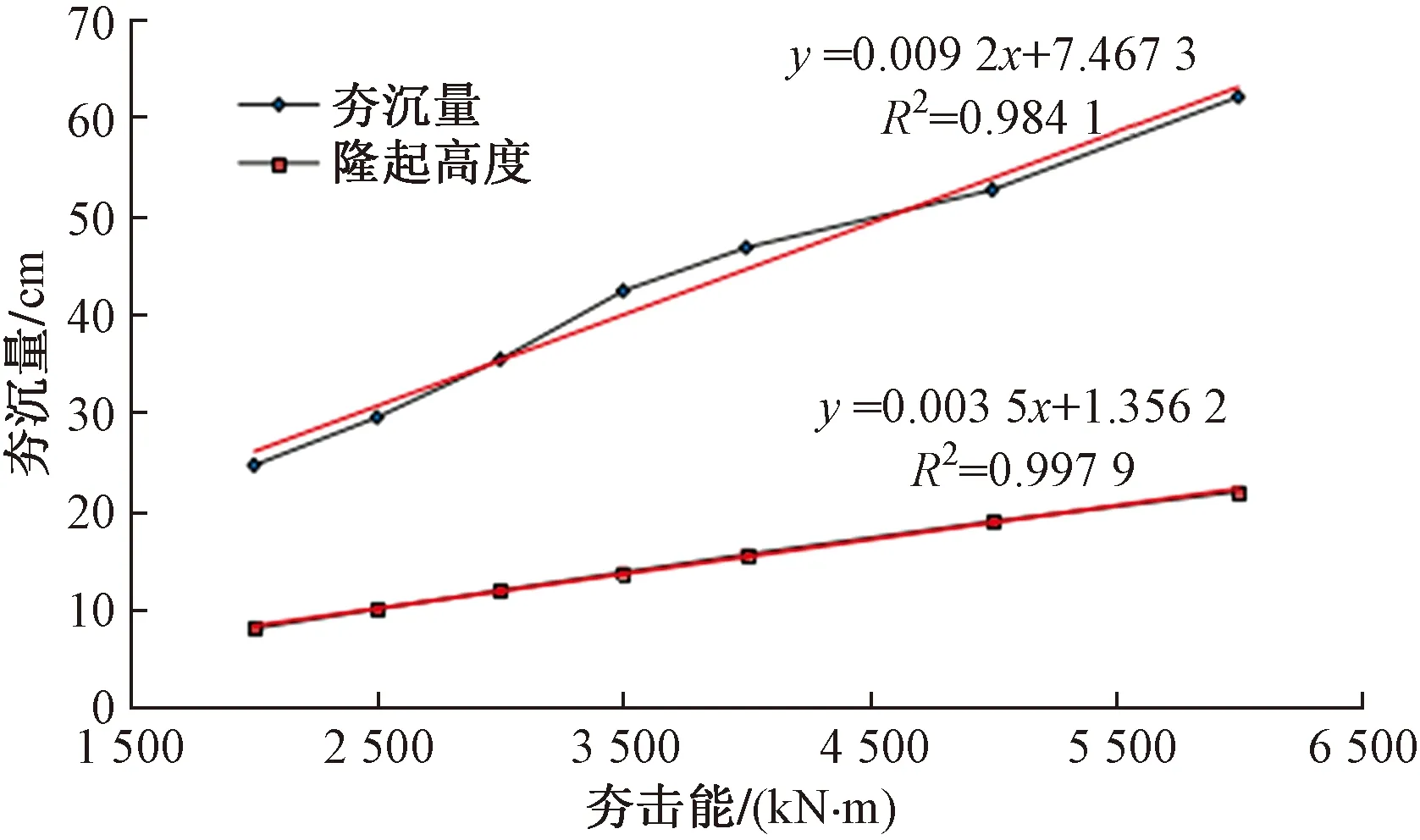
圖5 不同能級下地表變形

圖6 不同模量下地表變形

由圖7、圖8所示，在不同能級或同一沖擊能量不同深度下錘下土體豎向位移隨著時間的推移，呈現先迅速增大后減小最后逐步趨于穩定的狀態，說明在沖擊荷載作用下土體先出現彈塑性變形，隨時間推移彈性變形逐漸恢復，最后僅剩余塑性變形。分析圖8可知，隨著深度加深，最終土體產生的塑性變形逐漸減小，在6 m深度處最后彈性變形恢復后，塑性變形幾乎為零，這也說明在2 000 kN·m沖擊能量下土體的加固深度約為6 m。同時隨深度的增加，錘下土體出現位移變形的時間也不斷延后，最大位移出現時間約為0.22 s，說明能量隨時間推移不斷向深處傳遞。

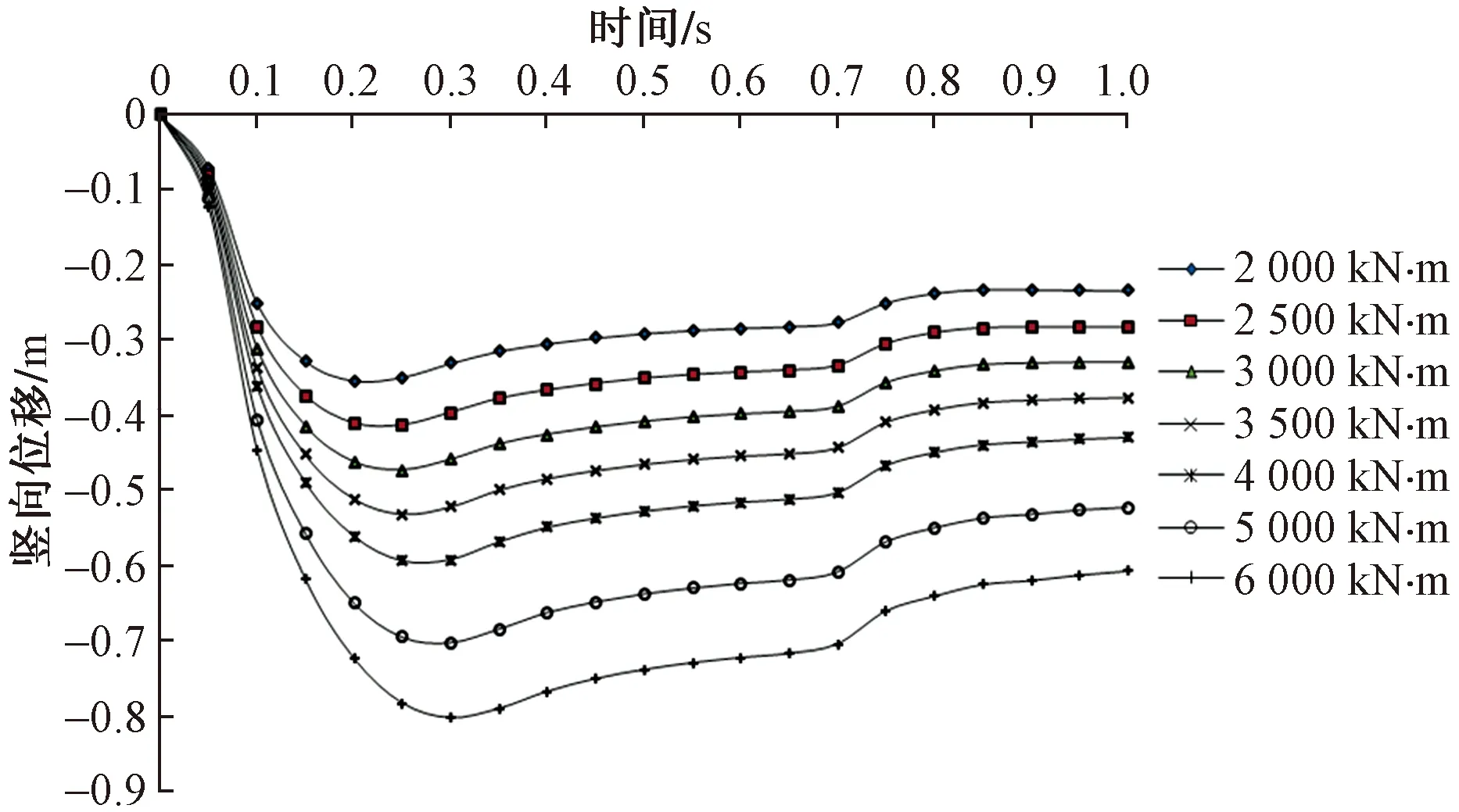
圖7 不同能級下豎向位移時程曲線

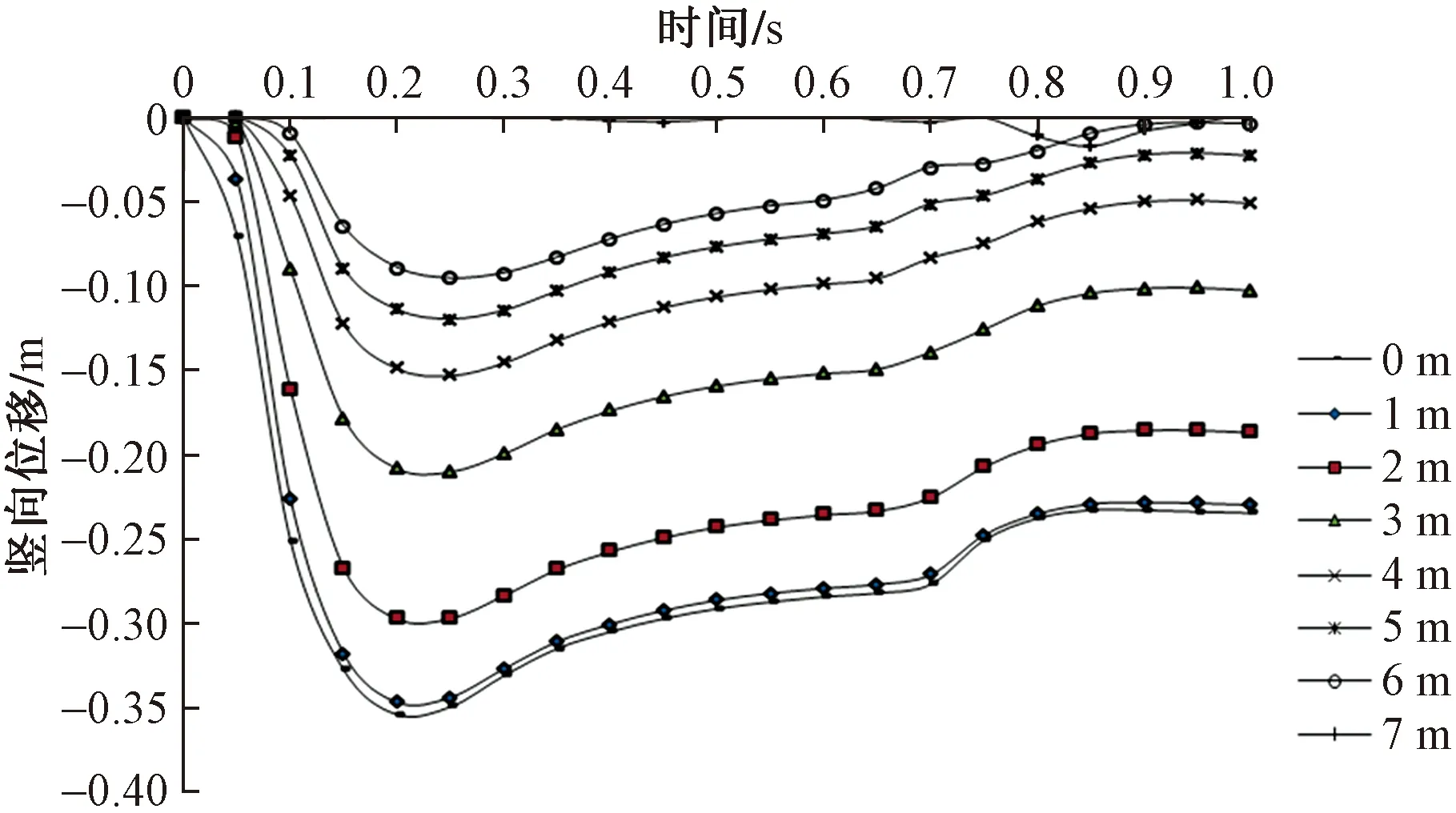
圖8 不同深度豎向位移時程曲線

由圖9、圖10不同沖擊能量和不同夯擊次數作用下不同深度處的豎向位移可以看出，隨著深度的增加豎向位移逐步減小。單次沖擊荷載作用下影響深度也為6.5 m左右，而隨夯擊次數增加影響深度不斷加深，第7次夯擊時影響深度已達9.6 m，說明在沖擊荷載作用下，錘下土體越來越密實，能量向下傳遞越來越多。

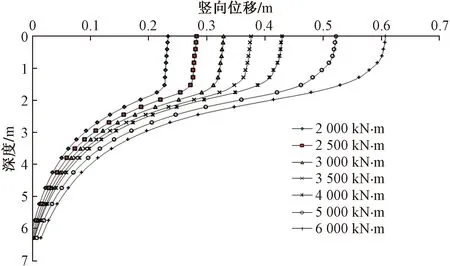
圖9 不同能級下豎向位移-深度曲線

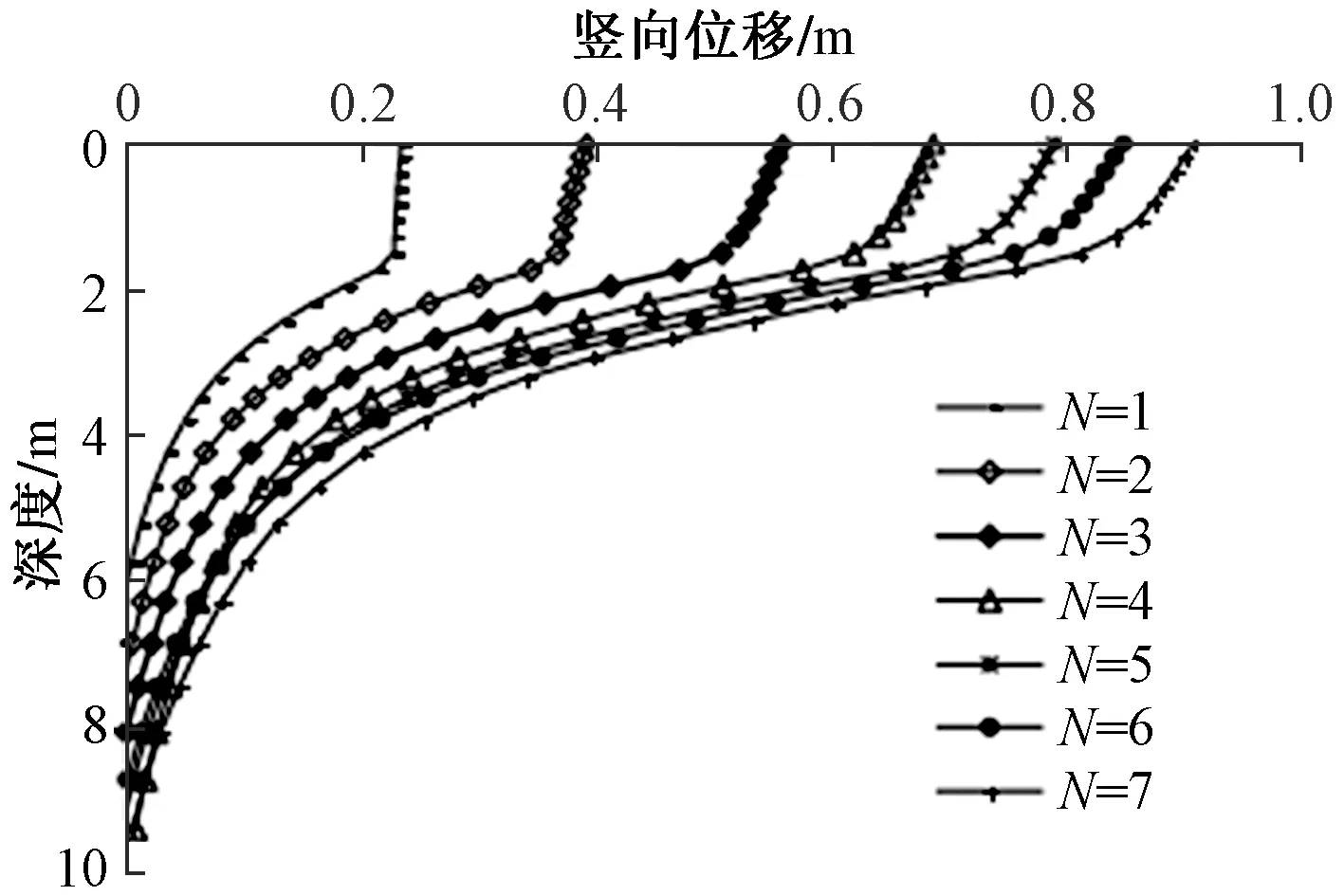
圖10 不同夯擊次數下豎向位移-深度曲線

2.3 強夯動力特性計算結果分析

圖11、圖12所示為錘下土體不同深度豎向應力和距離中軸線不同距離的垂直速度的時程曲線，豎向應力最大值出現在0.05～0.1 s，且隨著深度的增加最大豎向位移逐漸減小；周邊土體距離中軸線距離越遠振動垂直速度越小，且隨時間推移不斷衰減，出現最大豎向應力和垂直速度的時間隨著深度和與中軸線距離而延遲。沖擊荷載引起的土體震動會對一定范圍內周邊構筑物產生影響，在施工過程中應設置安全距離或設置隔振溝等措施。

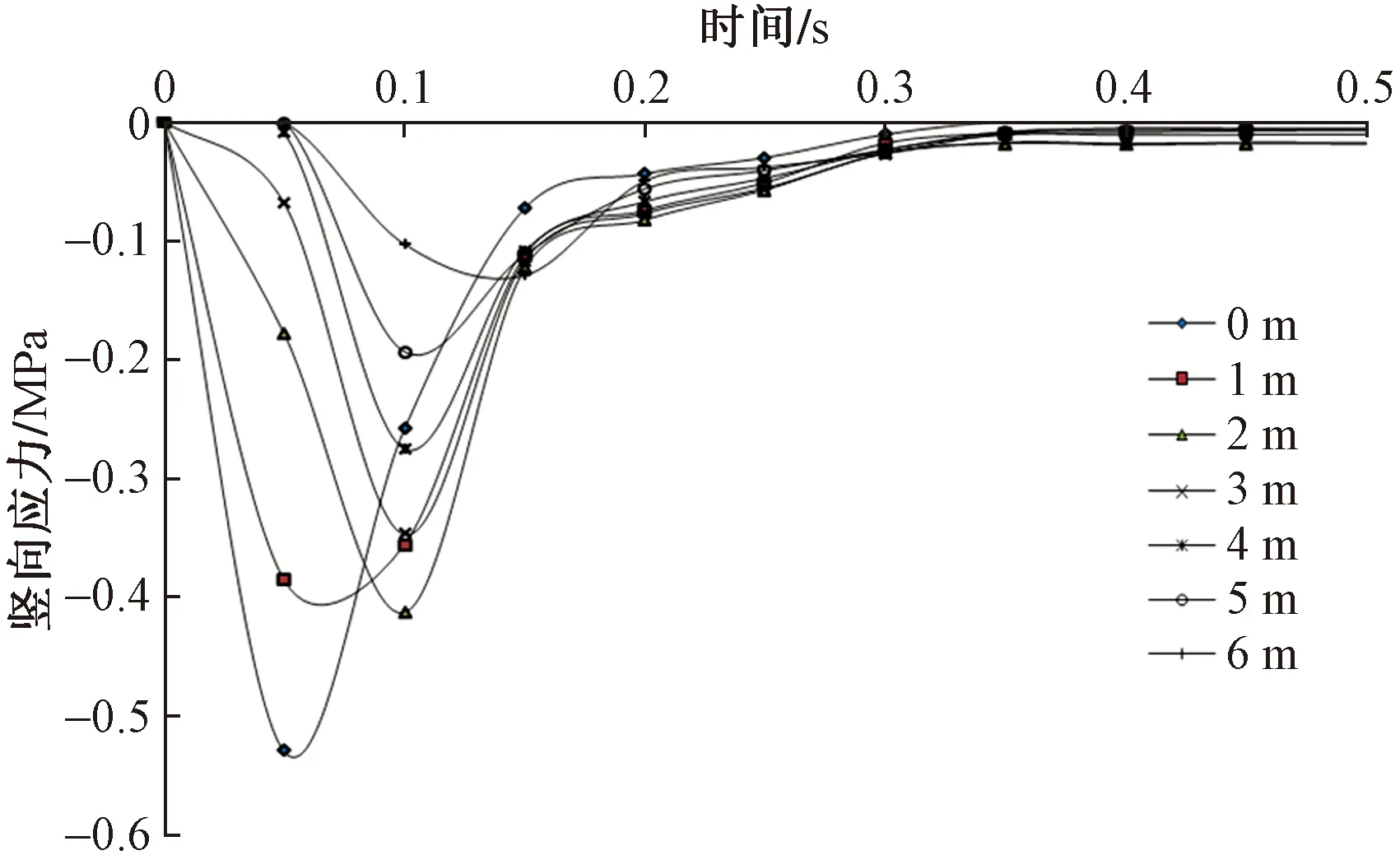
圖11 豎向應力時程曲線

圖12 垂直速度時程曲線

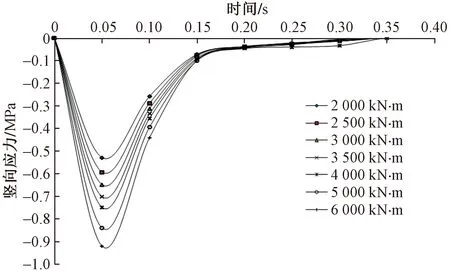
圖13 豎向應力時程曲線

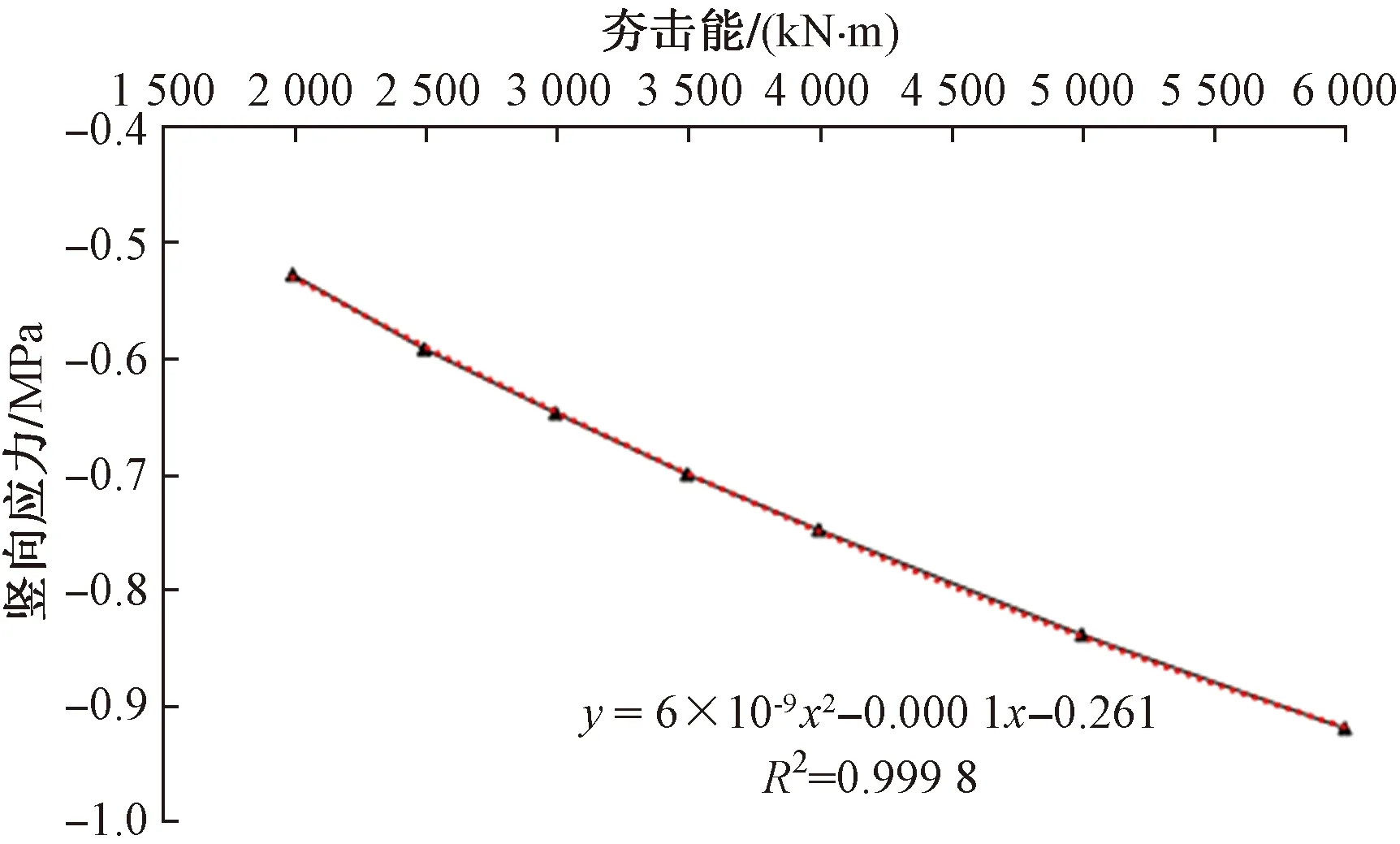
圖14 夯擊能-峰值豎向應力關系

由圖13、圖14可以看出，不同能級沖擊荷載作用下，豎向應力時程曲線呈近似三角形形狀，僅出現一次峰值應力，且隨著夯擊能增加豎向應力峰值越來越大，近似二次函數關系y=6×10-9x2+0.000 1x-0.261(x為夯擊能，y為峰值豎向應力)。隨夯擊能增加，在能量轉換過程中更多的轉換為土體內部勢能和摩擦熱能，所以擬合曲線呈現非直線關系。

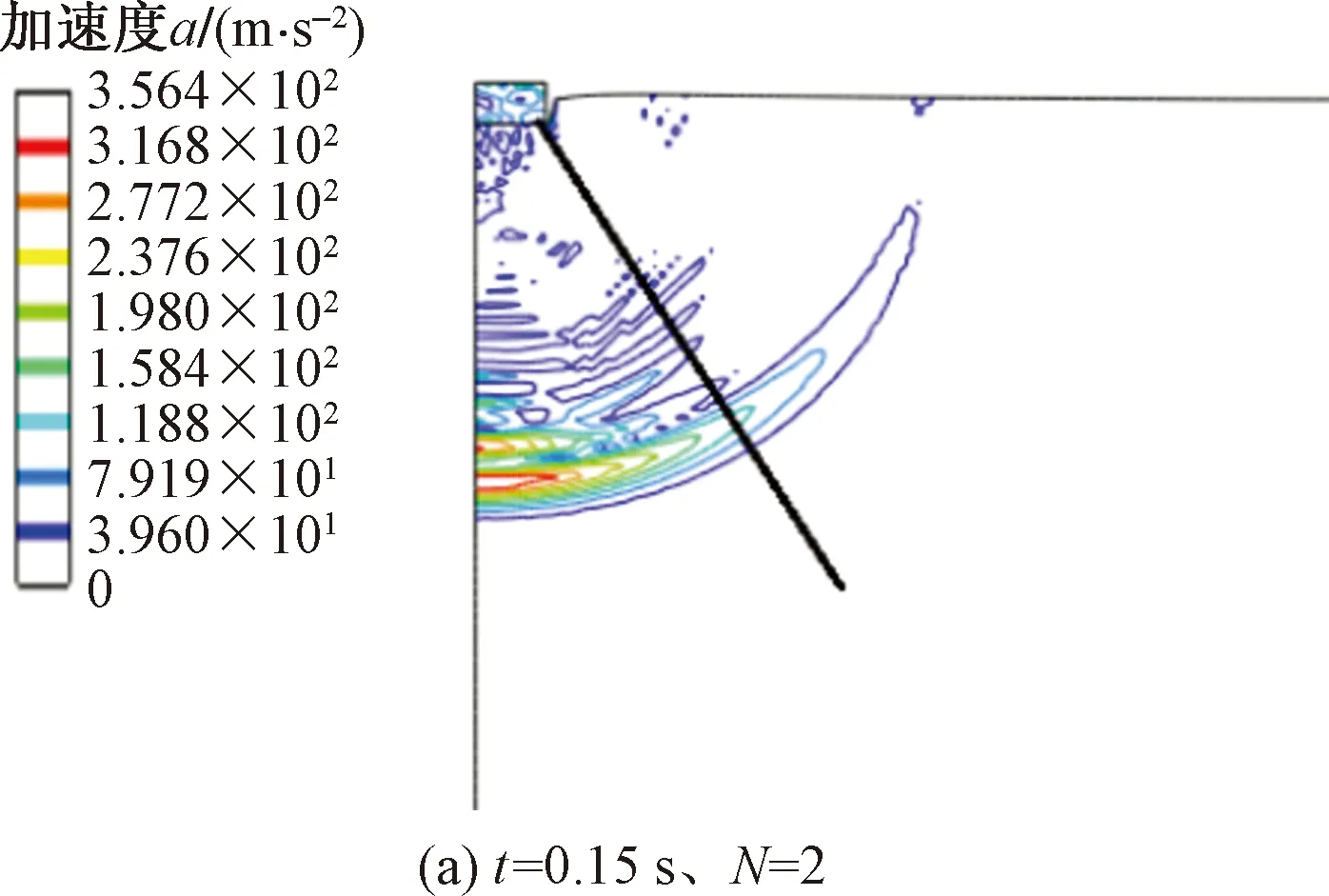
圖15 加速度等值線

圖15所示為沖擊能量E=2 000 kN·m、t=0.15 s、沖擊次數N分別為2、7時錘下土體顆粒振動加速度等值線圖，加速度沿40°～45°向下傳播，能量傳播過程伴隨著土體顆粒高速振動，從而使地基土體得以處理，在施工過程宜合理確定夯間距，分遍錯位夯實，確保土體得以有效處理。

3 結論

根據工程實際土體參數建立計算模型，計算結果與試驗結果較為相似，說明模型具有合理性，進而計算分析得結論如下。

(1)錘下土體沉降量與周邊隆起量隨夯擊能增加呈線性增長狀態：y=0.009 2x+7.467 3，y=0.003 5x+1.356 2；當彈模E>10 MPa時，錘下土體沉降量與土體彈性模量為線性關系：y=-0.116 6x+25.296，隆起高度隨彈模增大而漸小且逐步趨于平穩，說明彈模較大時土體在沖擊荷載作用下塑性變形愈發不明顯，而彈模E<10 MPa時，土體在錘體沖剪作用下主要產生塑性變形。

(2)在沖擊荷載作用下土體先出現彈塑性變形，隨時間推移彈性變形逐漸恢復，最后僅剩余塑性變形，隨著深度加深，最終土體產生的塑性變形逐漸減小，錘下土體出現位移變形的時間也不斷延后，最大位移出現時間約為0.22 s，說明能量隨時間推移不斷向深處傳遞，且錘下土體越來越密實，能量向下傳遞越來越多。

(3)豎向應力時程曲線呈近似三角形形狀，僅出現一次峰值應力，且隨著夯擊能增加豎向應力峰值越來越大，近似二次函數關系y=6×10-9x2+0.000 1x-0.261。隨夯擊能增加，在能量轉換過程中更多的轉換為土體內部勢能和摩擦熱能，所以擬合曲線呈現非直線關系。

(4)沖擊能量在碰撞發生后沿40°～45°向下傳遞，且不斷衰減。能量傳播過程伴隨著土體顆粒高速振動，從而使地基土體得以處理，在施工過程宜合理確定夯間距，分遍錯位夯實，確保土體得以有效處理。