板材沖壓成形過程有限元網格優化算法＊

高孝書，王旭東

板材沖壓成形過程有限元網格優化算法＊

高孝書1，王旭東2

（1.寧夏職業技術學院（寧夏廣播電視大學），寧夏 銀川 750021；2.寧夏鎂業有限公司，寧夏 銀川 750021）

板材沖壓成形是一個復雜的大變形過程，包含幾何非線性、材料非線性、接觸非線性等強非線性問題。因板材局部大變形導致有限元網格形狀的畸變，會嚴重降低有限元網格質量，甚至造成模擬計算失敗。針對此問題，提出了一種有限元網格優化算法，通過消除碎小單元網格和優化網格形態的方法，賦予網格節點結構關聯權重，量化網格節點加疊值，在保留板材變形模型特征及精度的同時，優化了板材沖壓成形的有限元網格，以實例模型驗證了算法的有效性。

板材沖壓；結構關聯權重；加疊值；有限元網格

在板材沖壓成形有限元模擬過程中，由于沖壓模具幾何結構的復雜性，板材隨沖壓進程產生局部非線性大變形，使得有限元網格劃分[1]時生成大量碎小或狹長的劣質單元。這些劣質單元將造成后期有限元分析結果的不穩定或迭代計算不收斂[2]，因此有限元網格的形態優化是決定模擬計算成敗的關鍵。

有限元網格優化算法是在保持板材變形模型特征及精度的前提下，賦予有限元網格節點結構關聯權重，建立網格節點結構關聯權重計算規則和網格節點加疊規則，量化網格節點加疊值，通過定向移動和合并網格節點實現網格節點的加疊，消除碎小或狹長的劣質單元，達到優化網格形態、提高網格質量的目的。

1 加疊算法

目前國內外主要的網格簡化算法有加疊簡化算法[3]、頂點聚類簡化算法[4]、區域合并簡化算法等。加疊算法是選取三角網格中小于臨界點距的2個點（和），將其中一個點加疊映射至點，然后修改拓撲關系，刪除多余的邊和面，完成簡化操作。一次簡化可以減少源模型的1條邊和2個面。加疊過程如圖1所示，算法將點加疊映射至點，三角形④⑧在加疊后從原網格中消失，而三角形⑤⑥⑦的頂點由點修改至點，網格形態發生了變化。

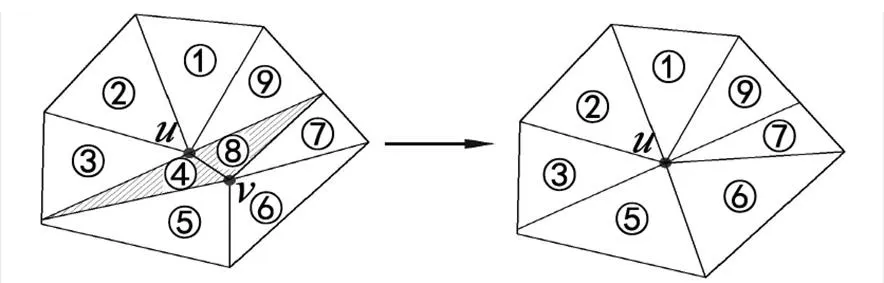
圖1 加疊過程示意圖

加疊后采用原始頂點，不引入新的頂點，不需要額外存儲計算節點，有效簡化了算法的復雜程度。通過連續多次加疊操作，直到滿足需要的簡化目標為止。

1.1 確定臨界點距

臨界點距m是判定啟動加疊簡化算法的一個閾值，即在三角網格中任意兩點之間的距離（簡稱點距）小于此閾值時，開始啟動疊簡化算法，通過特定節點的加疊和拓撲關系的修訂，消除碎小或狹長的劣質單元，實現有限元網格優化的目的。

當臨界點距選取過小時，加疊量過小，有限元網格優化程度不足；當臨界點距選取過大時，需要加疊的次數越多，加疊計算量越大，網格簡化程度也越大，局部區域過度簡化，易導致板材變形模型精度的降低，影響后期有限元分析的準確性或迭代計算的收斂性。因此，選取的臨界點距是否合適，將直接影響網格質量和有限元計算效率。

1.2 確定加疊映射點

加疊方向如圖2所示。選定臨界點距m后，對應的點和點有兩條加疊路徑：點加疊映射到點，如圖2（b）所示；點加疊映射點，如圖2（c）所示。

圖2 加疊方向示意圖

為保持板材變形模型精度和有限元模型準確度，需保留更重要、更具有代表性的網格節點，即判斷點和點的取舍問題。本文從網格節點結構關聯權重入手，通過量化節點的加疊值來量化節點的重要程度，優先保留結構關聯權重較大的節點，保證有限元分析的準確性。

分析沖壓模具幾何結構特征，對板材重要變形部位（如凸模圓角半徑或直壁圓角半徑較小處）和板材破裂高風險部位（如拉深變形聚集處或非弧面過度處）賦予結構關聯權重，權重值與特征性、重要性、風險性成正比。根據結構關聯權重計算節點加疊值，算法如下。

設某節點的節點加疊值為，結構關聯權重為，節點處有個相關權重i（1≤≤），則節點的加疊值的公式如下：

通過比較、兩點的節點加疊值為，可以解決、兩點的取舍問題，從而確定加疊映射點。

1.3 確定加疊順序

鄰接節點組間接加疊如圖3所示。確定加疊映射點后，需要確定加疊順序。當點距小于臨界點距m的節點組為鄰接關系時，其中一個節點組的加疊可能會影響另一個節點組的點距，不同的加疊順序會導致不同的加疊效率。如圖3中點距uv和vw是小于臨界點距m的鄰接節點組，當點加疊映射至點時，vw拉長等于uw，若uw大于臨界點距m，則通過一次加疊操作，間接完成了兩個節點組的加疊任務，很大程度上減少了加疊的次數和節點移動的距離，對提升加疊效率和板材變形模型精度具有重要意義。

圖3 鄰接節點組間接加疊示意圖

為了達到這一目的，在進行網格優化時，應先對點距小于臨界點距m的節點組進行排序，優先加疊點距最短的節點組，充分利用間接加疊效應，用最少的加疊次數和節點移動的距離實現有限元網格的優化。但是這種算法的缺陷是每次加疊后，被加疊節點的點距發生了變化，破壞了加疊前的排序。若每次加疊后都重新排序，則會增加很多計算量，反而降低優化效率。

為了避免重新排序，本文提出鄰接均值排序法。由于加疊只會影響與之鄰接的節點組點距，因此非鄰接節點組不予考慮。在對點距小于臨界點距m的節點組進行排序時，若節點組存在（≥0）個彼此鄰接的節點組，則此個彼此鄰接節點組的鄰接均值點距a為：

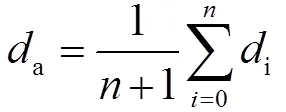
依據鄰接均值點距a，對所有小于臨界點距m的節點組進行組外總體排序；依據各節點組點距i，對鄰接節點組進行組內排序。按照排序依次進行加疊。在加疊鄰接節點組時，每次加疊后對組內節點組的i與m比較，直至組內i＜m的所有節點組加疊完畢；在加疊非鄰接節點組時，不需要考慮其他節點組的影響，按排序加疊即可。

1.4 加疊算法流程

本文的加疊算法基于臨界點距、節點結構關聯權重、加疊值三個要素，采用鄰接均值排序法，在避免重復排序的情況下，整體上實現了對點距較短節點組的優先加疊，加疊算法基本流程如圖4所示。

圖4 加疊算法流程圖

2 實例驗證

為了驗證加疊算法的有效性，利用NX10.0 Open API結合C++編程加疊算法，然后導入DEFORM有限元分析軟件，驗證加疊算法優化后網格的收斂性。實驗在Intel Core i7-9700K 3.6 GHz CPU，16 GB內存環境下進行。加疊前的板材沖壓成形有限元模型如圖5所示。A處部分網格加疊前后對比如圖6所示。

圖5 加疊前的板材沖壓成形有限元模型

圖6 A處網格加疊前后對比

從局部放大圖中可以明顯看出，由同一區域網格在加疊優化后很好地消除了狹長或碎小的單元網格，保留了板材變形模型特征及模型精度，達到了預期網格優化效果。文中加疊算法減少了排序和加疊次數，響應時間短、處理速度快、收斂效果好，在大型復雜板材沖壓成形有限元網格優化中效果顯著。

3 結語

文中加疊算法通過賦予網格節點結構關聯權重，量化節點加疊值，在保持板材變形模型特征及精度的同時，消除了網格中狹長或過于碎小的單元。通過實例驗證，加疊算法有效地優化了板材沖壓成形的有限元網格形態，提高了網格質量，具有較強的實用性。

［1］曹增歡，黃常標，鄭紅.三角網格模型的特征保持混合折疊簡化［J］.光學精密工程，2019，27（4）：971-983.

［2］章志兵，鄒騰，王麗榮，等.考慮結構特征權重的船舶有限元網格優化算法［J］.武漢理工大學學報， 2018，40（5）：89-94.

［3］HOPPE H，DEROSE T，DUCHAMP T.Mesh optimization ［C］//SIGGRAPH93. Anaheim：ACM Press，1993.

［4］ROSSIGNAC J，BORREL P.Multi-resolution 3D approximation for rendering complex scenes ［M］.Berlin：Springer-Verlag，1993.

高孝書（1986—），男，碩士，講師，主要研究方向為板材沖壓成形有限元數值模擬。王旭東（1972—），男，高級工程師，主要研究方向為鎂合金板材加工。

寧夏重點研發計劃基金資助（編號：2018BEE03027）；寧夏職業技術學院（寧夏廣播電視大學）重點研究項目（編號：XJ201802）；寧夏青年科技人才托舉工程（編號：2019TJGC053）

2095－6835（2020）06－0041－02

TG386

A

10.15913/j.cnki.kjycx.2020.06.013

〔編輯：嚴麗琴〕