深度學習在地質儲層屬性預測中的應用研究

侯 曉 琳

(北京大學地球與空間科學學院 北京 100871)

0 引 言

借助于計算機技術解決地質學相關問題的方法研究已經成為地質學科中的重點和熱點。地質體建模方法研究的目的就是能夠根據多來源地質數據，解釋較難直接觀察到的地質條件，分析并預測地質相關特征，采用可視化方式還原地質構造和巖石特征分布，為地質學科學研究和工程實踐提供理論依據[1-2]。目前，三維地質建模技術已經廣泛應用于油氣勘探開發、礦山開采、城市地質、資源儲量評價等多個領域的項目工程中[3-4]。三維地質建模主要包括構造建模和屬性建模。構造模型采用幾何網格結構表征斷層等地質界面、地質體之間拓撲關系，展示地質體儲層構造形態。屬性模型依賴于構造模型單元，量化表征地質儲層特征與巖石特征，反映地質屬性分布情況。地質屬性概念包含儲層屬性。儲層屬性主要是指如孔、滲、飽等反應儲層分布、巖性、物性等非均質性特征。地質屬性描述范圍更大，巖體的幾何特征如產狀、間距同樣屬于地質屬性，用來描述地質構造。

由于地下空間的變異性，利用有限地質數據和地質約束對地下空間屬性特征進行預測，建立地質儲層屬性模型是三維地質建模研究重點和難點。研究內容從克里金方法等確定性建模方法[5-6]，發展到序貫高斯建模等隨機建模方法[7]，再到多點指示方法[8]、模擬退火[9]、Simpat[10]等多點地質學統計方法，盡可能利用更多相關數據來推測地質體模型中未知地質儲層屬性值。地質體模型中地質單元的屬性值與其所在三維空間位置具有一定的關系，利用地質單元所在空間位置及其所在空間特征統計預測未知地質儲層屬性值具有一定的研究價值。

基于深度學習解決地質學問題的方法逐漸成為研究熱點，相較于在其他領域中已經獲得的應用成果，還有很多應用研究的空間和價值。目前，深度學習方法已在遙感圖像分類、礦物識別等關鍵研究領域獲得了一些成果[11]。張野等[12]基于巖石圖像利用深度學習遷移模型實現了巖性自動識別和分類。徐述騰等[13]利用Unet卷積神經網路模型實現了礦石礦物智能識別和分類。劉大偉等[14]利用深度信念網絡實現對高分辨率遙感影像的基于光譜-紋理特征的分類，有效提高分類精度。付超等[15]設計一種卷積神經網絡與支持向量機相結合的方法預測多波地震油氣儲層分布。段友祥等[16]采用卷積神經網絡應用于地質儲層參數預測，為儲層地質建模與測井資料解釋提供理論支持。還有很多地質學問題可嘗試采用深度學習方法解決，將更多的研究成果應用到油氣勘探開發等工程項目中，為決策提供數據支持和理論依據。

地質數據特點明顯，種類多樣，但樣本數量較少，獲取成本較高，空間分布不均，受限于測井、地震等地質數據獲取手段，地質儲層屬性建模方法受到地質數據樣本點分布的影響較大。通過分析空間中地質儲層屬性特征來預測某空間位置屬性值的方法具有一定的研究意義和價值。在三維空間中某點的地質儲層屬性值與其所在空間的屬性值特征具有一定的關系，以該點為中心，在一定距離為半徑的三維空間內的屬性值作為參考數據，計算空間屬性樣本點均值和方差的無偏估計，量化分析空間地質儲層屬性特征。空間統計特征值作為訓練數據，設計全連接網絡和一維卷積網絡，訓練并生成屬性預測網絡模型，實現三維空間中地質儲層屬性預測。

1 三維地質儲層屬性預測模型

1.1 研究思路

基于深度學習建立三維地質儲層屬性模型的主要研究實現思路見圖1。首先，從整理地質數據入手，地質數據可分成構造建模數據與屬性建模數據，采用構造建模數據分析地質元素(地層面、斷層、地質體等)之間拓撲關系，建立三維地質構造模型，選取合適的網格模型形式表達地質構造和地質元素之間的拓撲關系。基于構造網格模型，對地質儲層屬性樣本數據進行采樣，每個最小三維網格單元對應一個屬性值(例如六面體網格單元)。然后，分析網格單元所在三維空間分布特征，隨機地將采樣屬性值分成訓練集與驗證集兩個部分訓練深度學習網絡，建立三維網格單元的屬性預測模型。

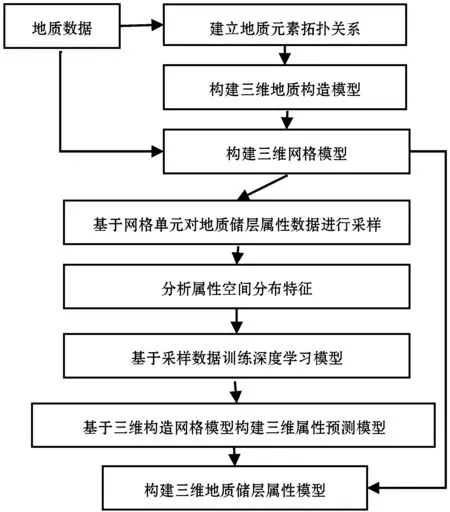
圖1 構建三維地質儲層屬性模型主要研究思路

通過分析地質儲層屬性分布特征，生成屬性分布特征數據，訓練全連接網絡和一維卷積網絡，生成地質儲層屬性預測模型。基于全區地質儲層屬性分布特征數據建立三維地質模型。

1.2 地質儲層屬性空間分布特征

利用有限的地質樣本數據計算地質區域局部特征，采用樣本均值和方差的無偏估計計算某個空間區域的地質儲層屬性均值和方差，作為特征樣本數據。

在三維空間中，假設某一網格單元Pi(六面體)所在的某個空間S內的所有樣本點屬性值表示為P1,P2,…,Pn,Pi=(xi,yi,zi,pi)。以Pi為中心，r1,r2,…,rm為半徑劃分m個球形子空間區域S1,S2,…,Sm，統計每個子空間Sj的屬性特征，包括屬性值均值和方差，其無偏估計可以分別表示為：

(1)

屬性樣本點pjk在子空間sj中。特征樣本數據的計算方式采用近鄰原則，以固定長度為半徑，計算多個半徑尺度下的子空間內樣本點屬性值的均值與方差作為訓練集特征數據。以二維平面空間內特征樣本計算為例說明(見圖2)，屬性網格點p1為中心，以半徑為r1、r2、r3、r4的子空間s1、s2、s3、s4分別計算樣本點期望和方差的無偏估計，在子空間s3中，屬性樣本點數據集合S3={p2,p3,p4,p5,p6,p7}，s3內屬性樣本均值和方差值為：

(2)

采用同樣方法計算并獲得4個空間區域的屬性值期望和方差(M1,V1)、(M2,V2)、(M3,V3)、(M4,V4)。通過研究多個子空間統計特征值與地質儲層屬性值之間的關系，確定屬性值受到子空間的影響范圍。

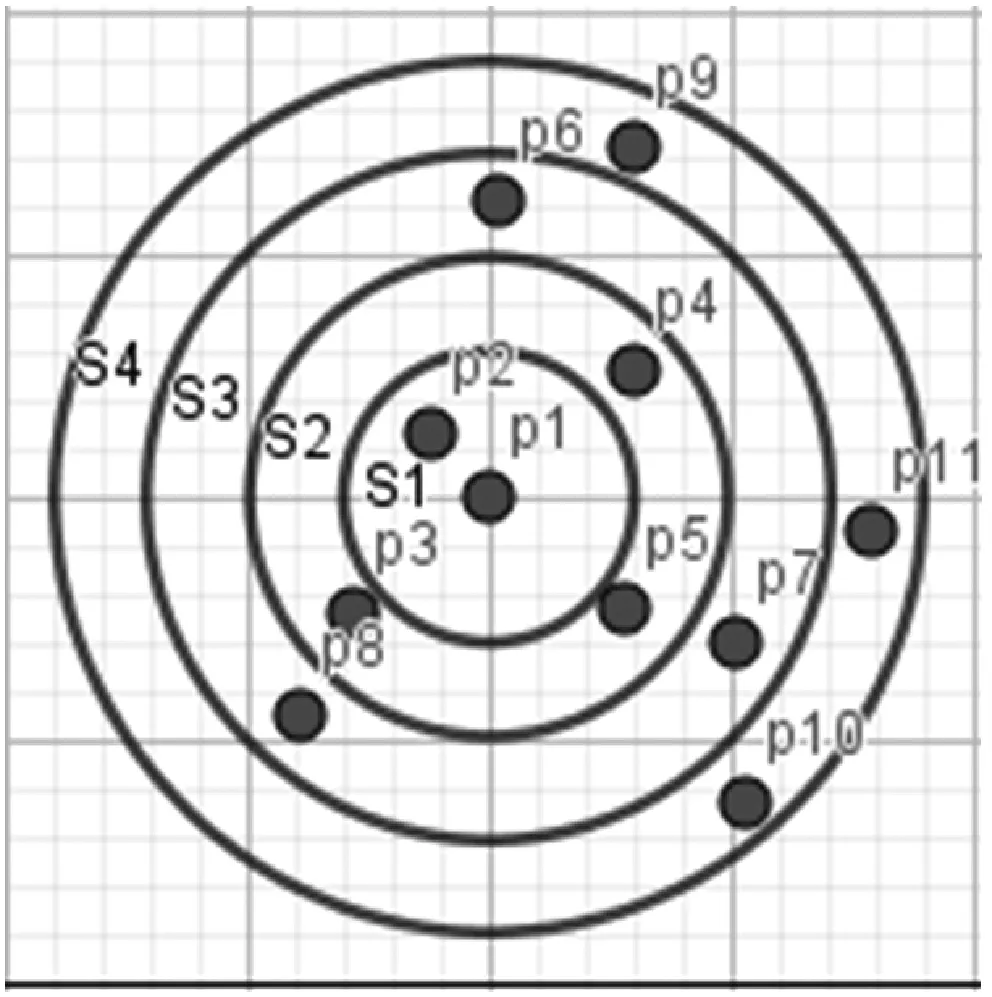
圖2 二維空間平面樣本點關系圖例

基于測井數據獲取地質儲層屬性數據，分析三維空間中網格單元屬性值與以其為中心的不同半徑的子空間中屬性期望值之間的關系。以某地質區塊A為例，該區塊內共有79口井(見圖3)。基于角點網格建立三維地質體構造模型，對測井數據進行抽樣作為屬性值樣本點，在區塊A中共有5 398個網格單元的屬性值樣本點，分析以這些網格單元樣本點為中心的子空間區域特征與網格單元屬性值之間的相關性。

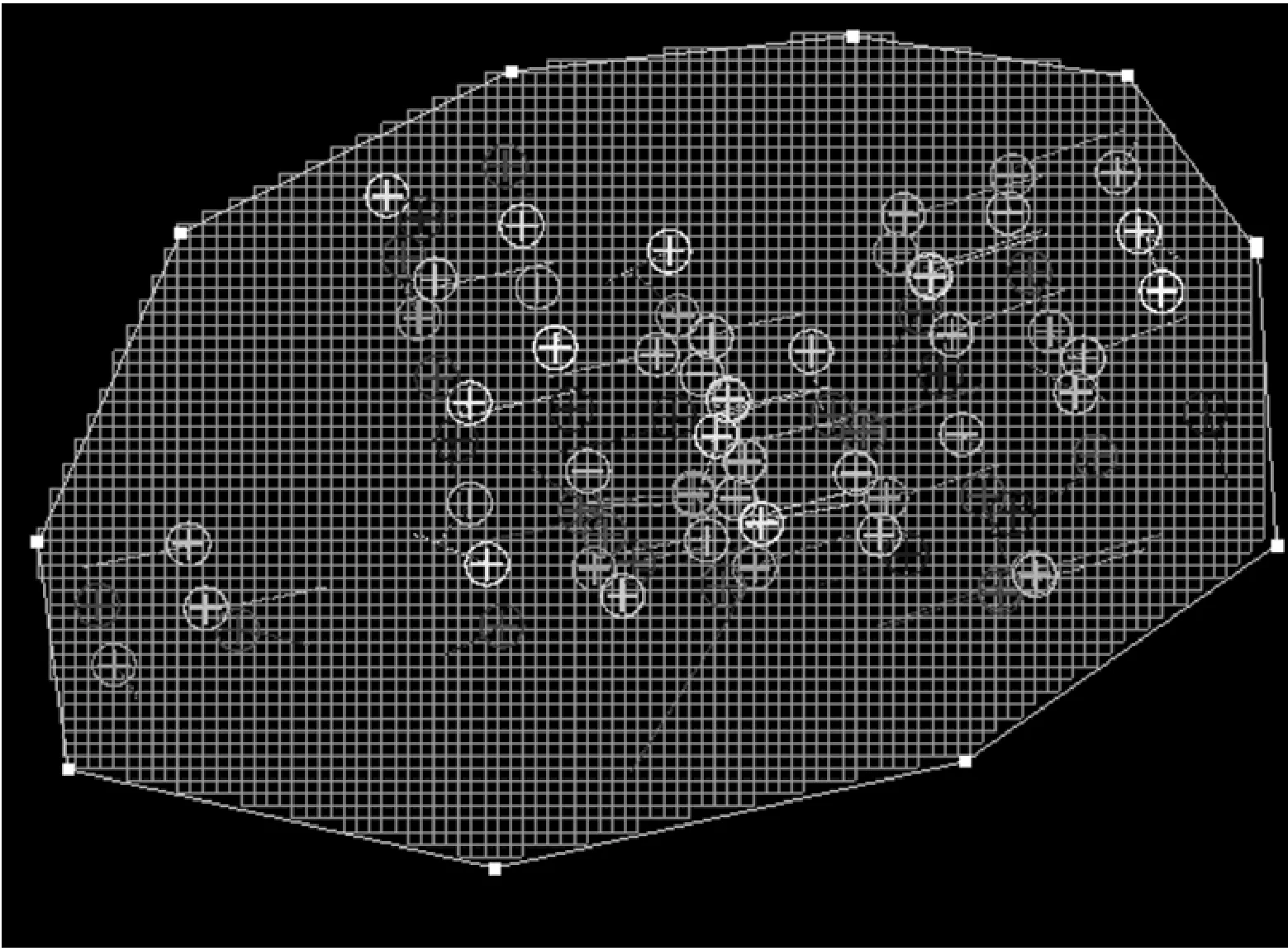
圖3 79口井所在地質區塊A俯視圖

以滲透率屬性為例，隨機選取某個網格單元，在以固定長度遞增半徑的多個子空間區域中期望和方差值如圖4所示。顯而易見，隨著子空間大小增加，子空間的均值和方差的變化規律明顯，均有兩次明顯跳躍，這是由于不斷增加子空間的范圍引入新的屬性樣本點會導致子空間特征發生較大的改變。因此，只有一定范圍內的子空間特征與待測屬性的地質單元具有一定的相關性，僅需要在一定范圍獲取子空間的特征數據作為訓練數據集。

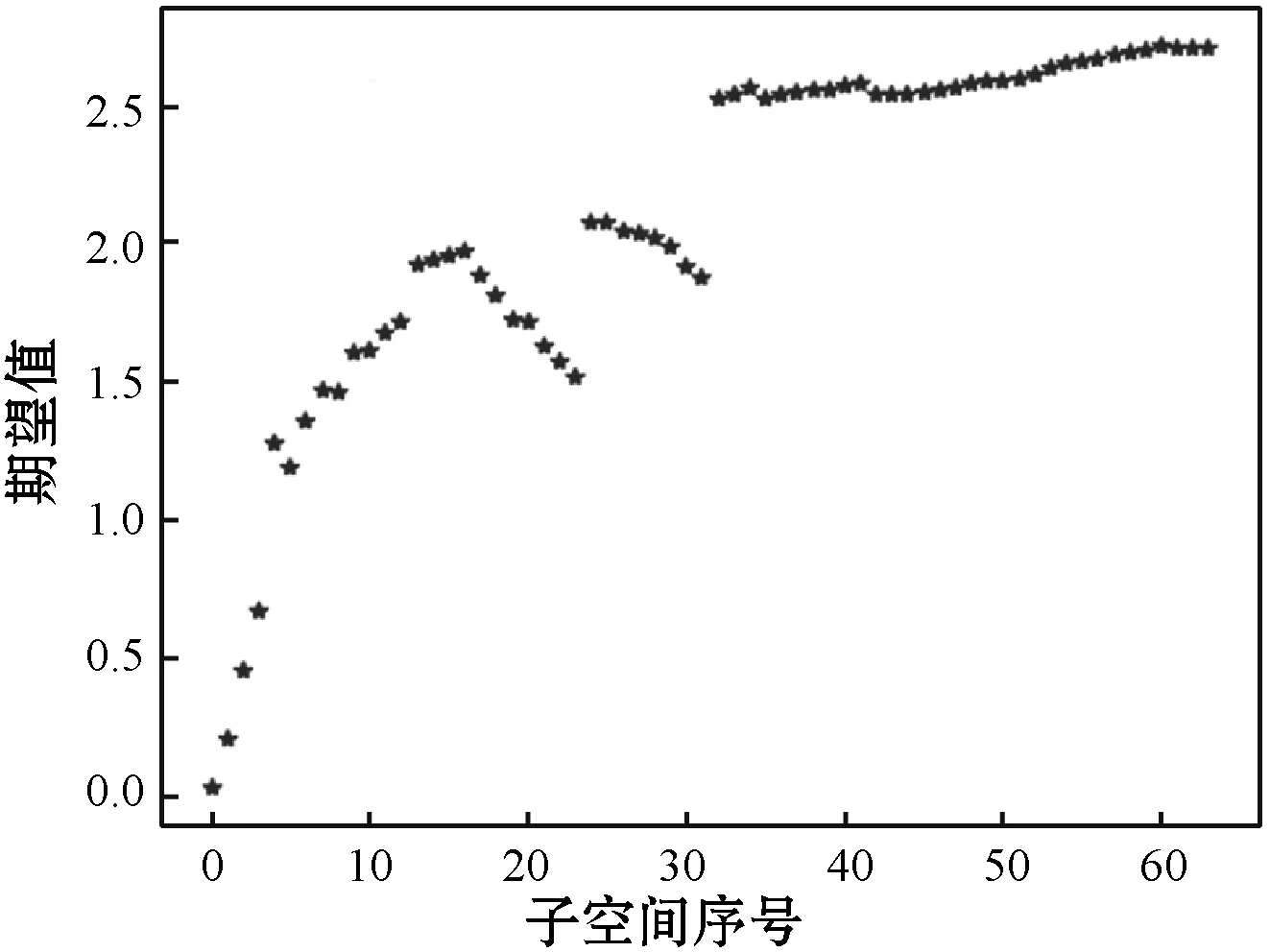
(a) 多個空間區域滲透率屬性期望值

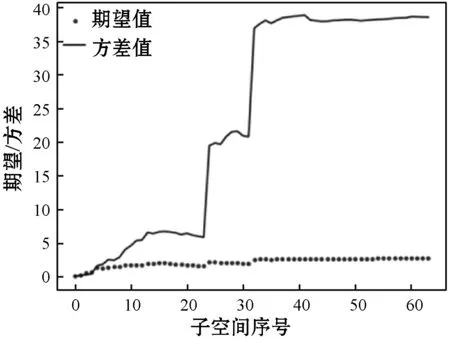
(b) 多個空間區域滲透率屬性期望值與方差值圖4 某網格單元為中心的多個子空間均值和方差特征圖

不失一般性，隨機抽取5個網格單元滲透率屬性樣本點，以各自為中心的子空間特征統計期望值與方差見圖5，子空間期望和方差的變化規律具有相似性。在三維空間中，以網格單元為中心的前15個子空間與該網格單元滲透率屬性值具有一定的相關性，將這15個子空間期望值特征作為訓練數據，利用這些具有一定相關性的子空間特征值訓練并建立深度學習模型來預測單元網格點屬性。

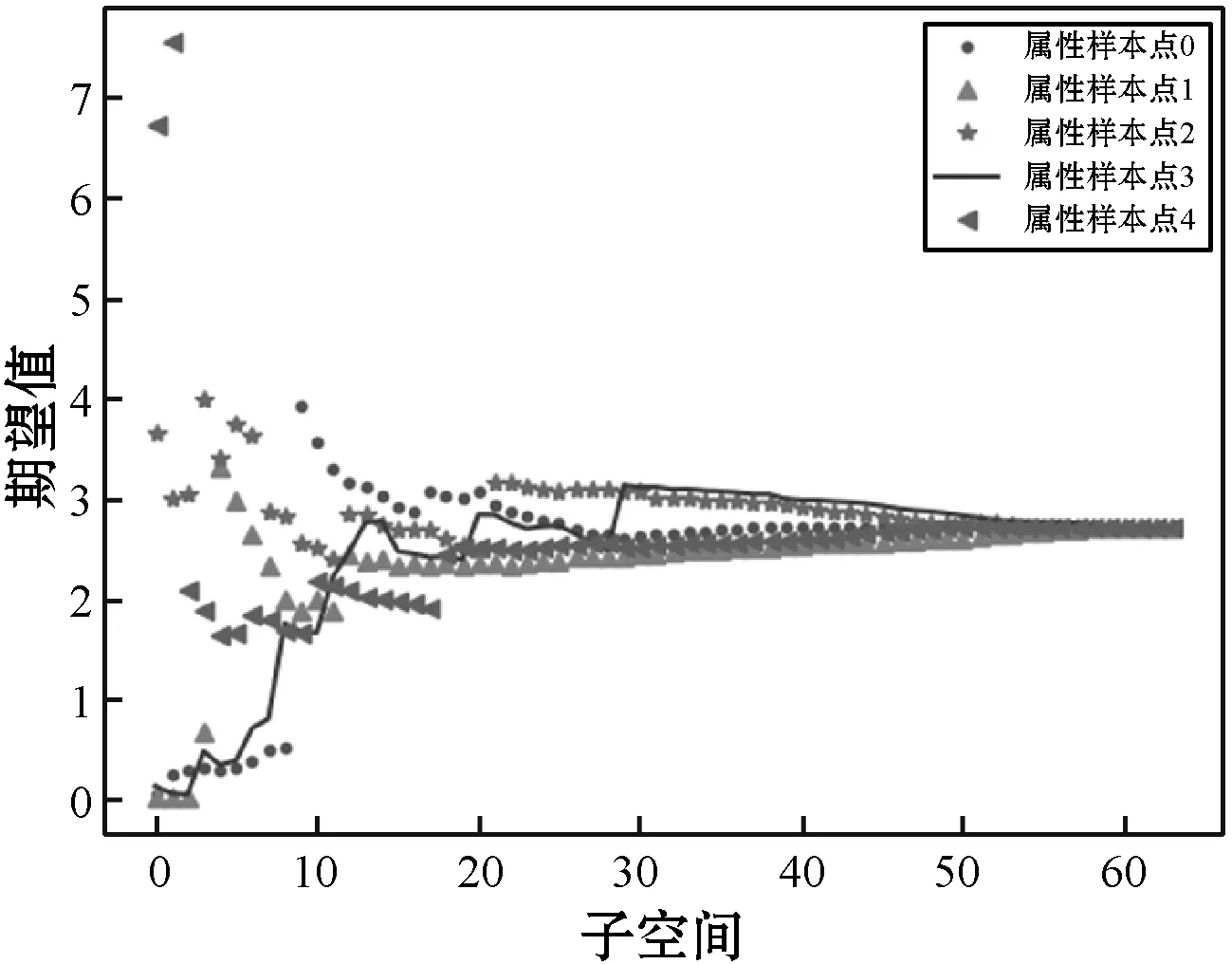
(a) 多個空間滲透率期望值

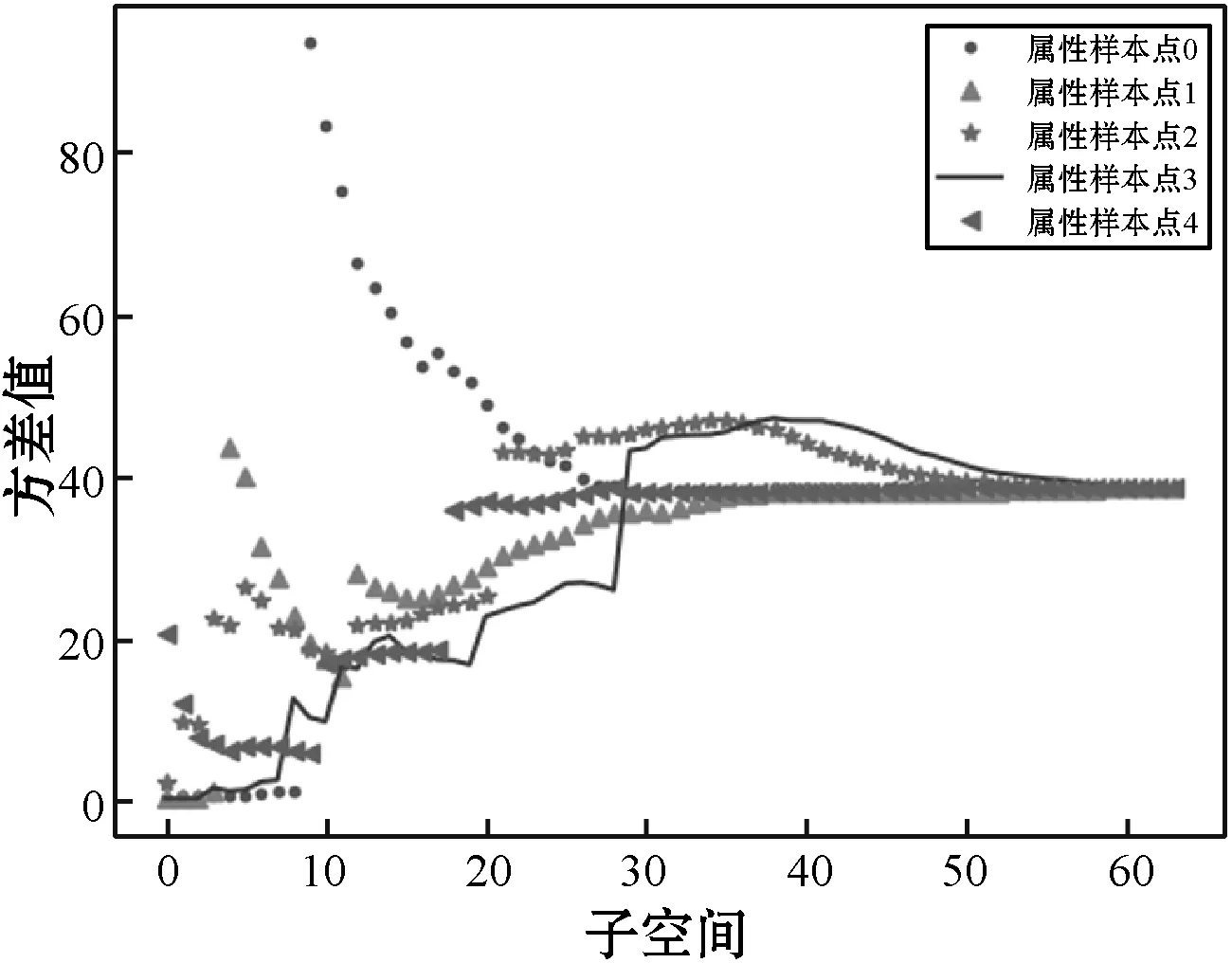
(b) 多個空間滲透率方差值圖5 以5個隨機網格單元為中心的多個子空間 滲透率期望值與方差值

2 基于深度學習網絡儲層屬性預測

采用實際地質儲層屬性值樣本點數據，基于深度學習網絡，以網格單元為中心的n個子空間屬性特征期望值作為輸入，預測屬性值作為輸出值，建立并訓練深度學習網絡模型預測三維地質體網格單元點的屬性值。本文將采用全連接網絡和卷積網絡兩種模型建立三維地質體屬性預測模型，對比分析訓練集與驗證集屬性預測屬性值與實際屬性值，評估網絡模型預測效果。

2.1 全連接網絡模型屬性預測模型

在深度學習方法中，全連接網絡作為基礎模型，應用廣泛。基于全連接網絡建立屬性預測模型，網格單元i屬性值pi(y)作為一維輸出層，以其為中心的n個子空間特征期望值(x1,x2,…,xn)作為n維輸入層。全連接網絡模型包含一個n維輸入層、一個一維輸出層、三個隱藏層(見圖6)，其中隱藏層i、隱藏層j、隱藏層k維度為32、32和16，并分別在三個隱藏層后連接三個激活層(tanh函數，tanh函數，relu函數)，建立非線性屬性預測模型。

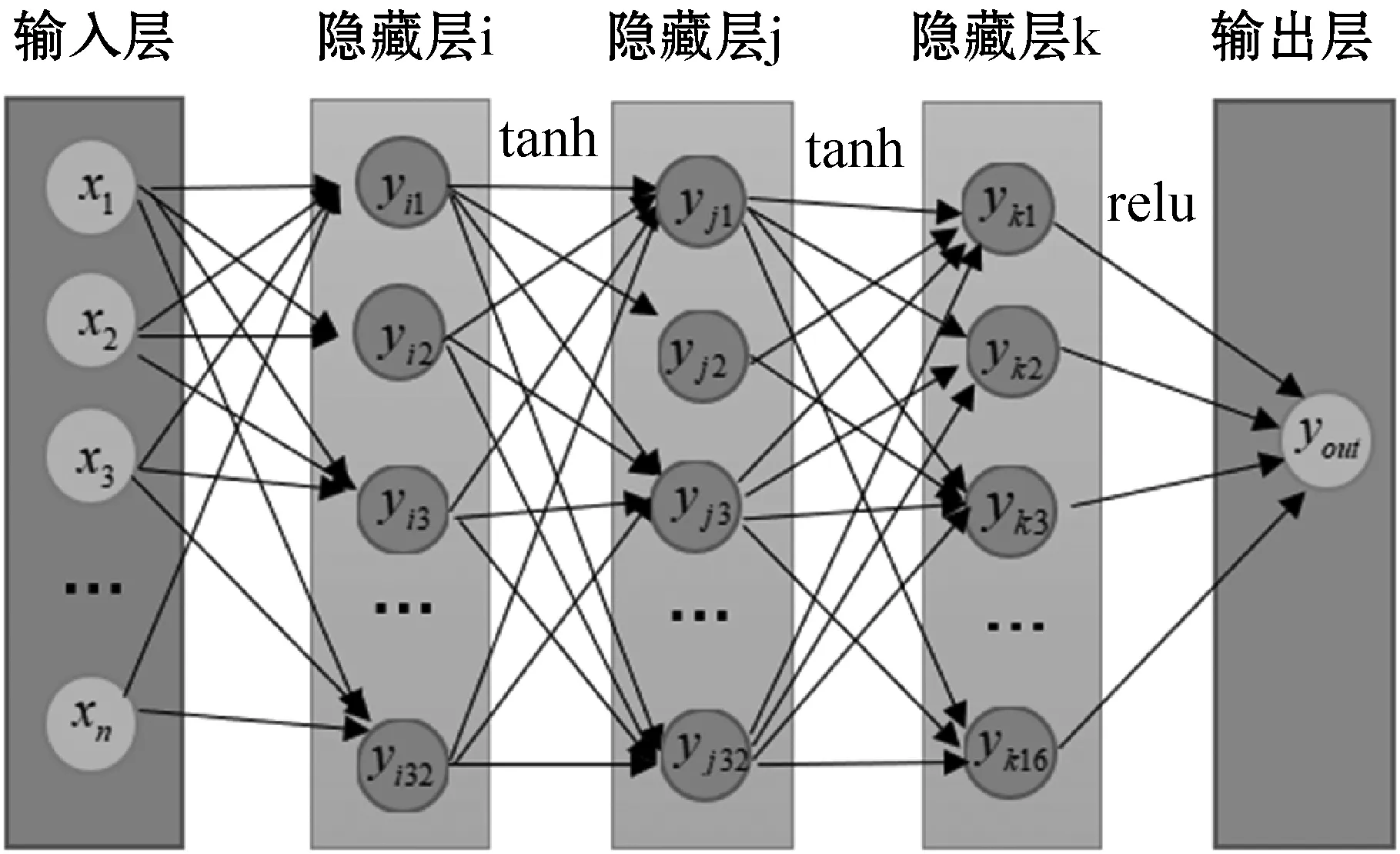
圖6 全連接網絡結構設計圖

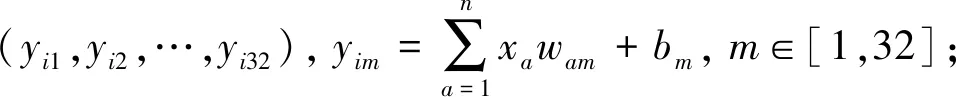
屬性預測模型由三層全連接網絡構成，采用隨機梯度下降作為優化器，初始學習率設置為0.001，每次遍歷訓練樣本，學習率自動下降50%，直至損失函數值達到穩定狀態停止訓練。全連接網絡設計偽代碼如下：

Input=Input(size=n)

fc1=FullyConnection(size=32,activation=′tanh′)

fc2=FullyConnection(size=32,activation=′tanh′)

fc3=FullyConnection(size=16,activation=′relu′)

output=Output(size=1)

model.add(Input,fc1,fc2,fc3,output)

以地質區塊A的儲層滲透率屬性(單位md)預測為例，通過三維空間特征分析，采用地質單元所在的15個子空間的期望值作為15維輸入數據，利用主成分分析方法(PCA)將15維數據降至8維，這8維數據將作為全連接網絡模型的輸入數據。5 398個地質單元滲透率屬性值分布如圖7所示。

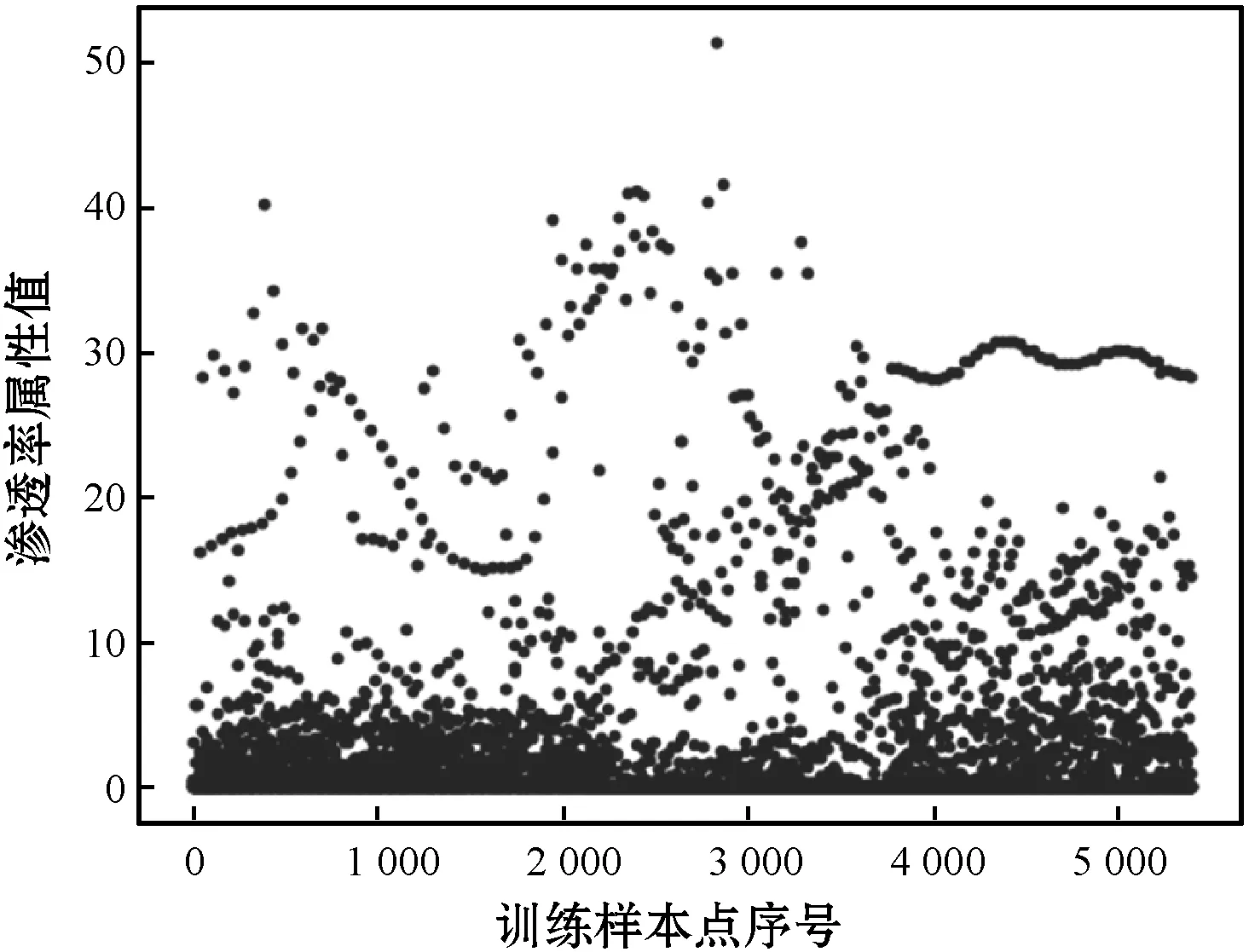
(a) 屬性值分布

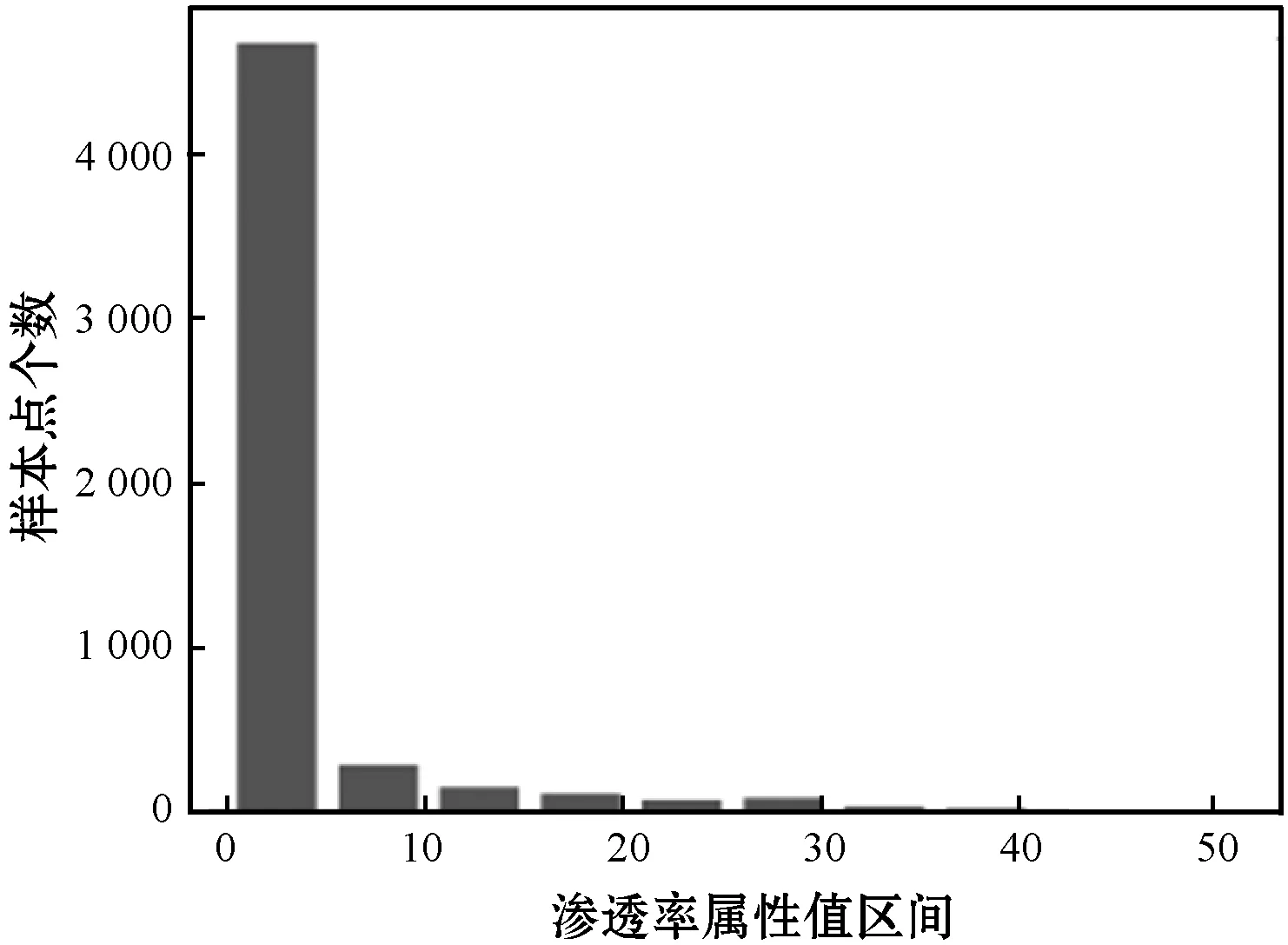
(b) 屬性值直方圖統計圖圖7 儲層滲透率屬性樣本分布

在5 398個地質單元滲透率屬性樣本點中，隨機選取80%數據作為訓練集，20%數據作為驗證集，訓練全連接網絡模型，直到損失函數值不再呈現下降趨勢為止。采用訓練后獲得的全連接網絡模型對訓練集數據和驗證集數據進行預測，訓練集與驗證集的預測值與實際值對比如圖8所示。多數網格單元屬性預測值與實際值相近，預測效果較好，少數單元網格屬性值預測存在一些偏差，全連接網絡結構能夠較好地學習到滲透率屬性的預測規律。

(a) 滲透率屬性訓練集數據真實值與預測值對比

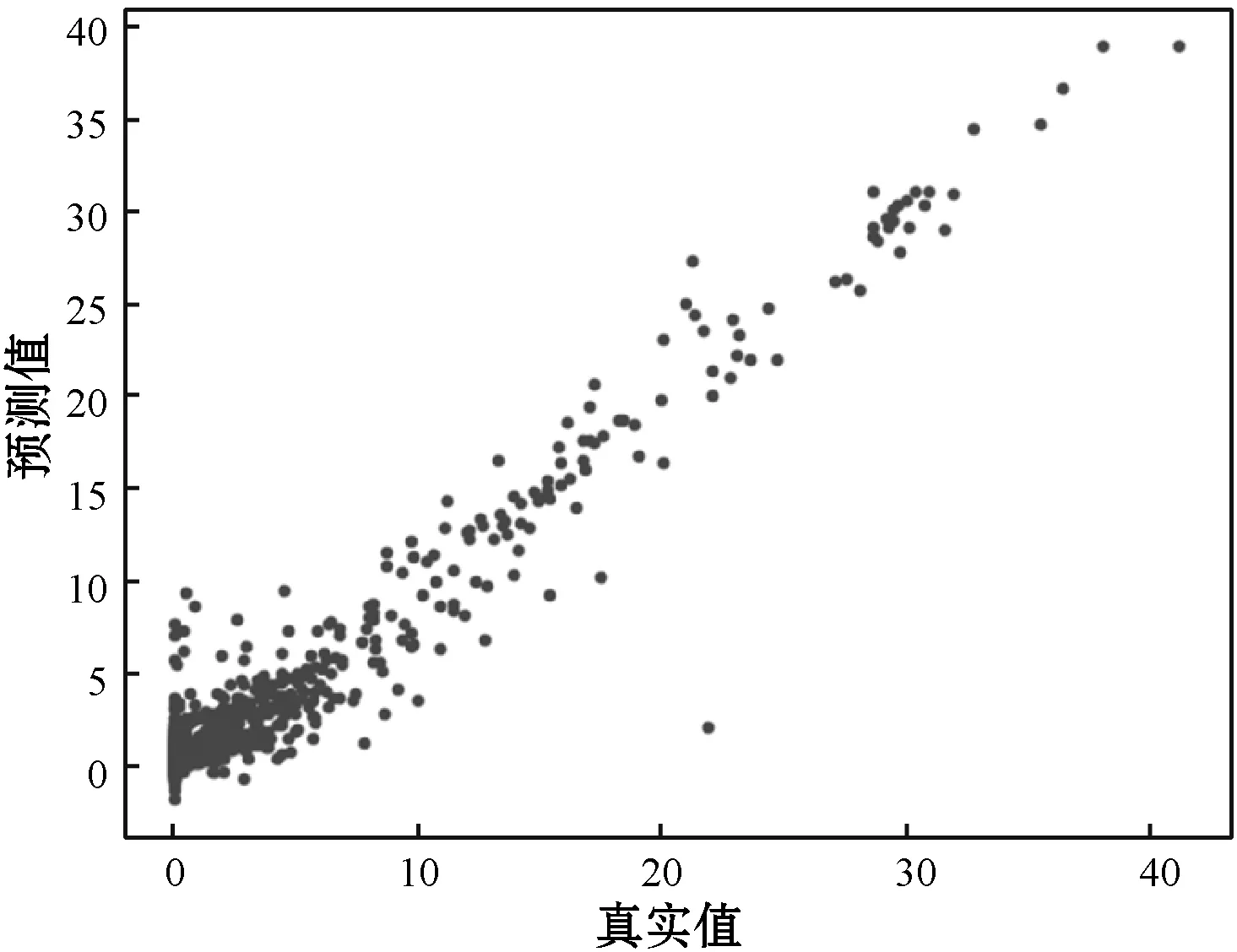
(b) 滲透率屬性驗證集數據真實值與預測值對比圖8 滲透率屬性訓練集與驗證集預測值與真實值對比

基于全連接網絡模型和三維構造模型，未知滲透率屬性值網格單元所在空間期望值作為輸入值，預測地質區塊A的地質單元滲透率屬性值，生成三維滲透率屬性模型,如圖9所示。

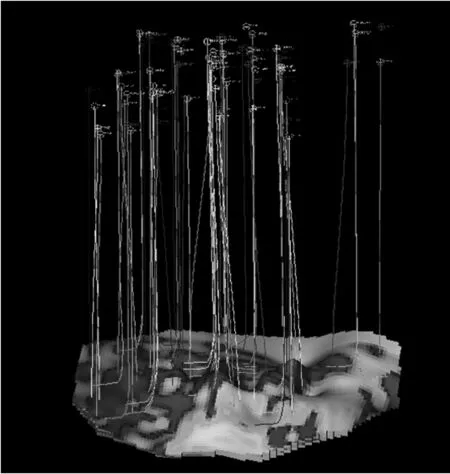
圖9 地質區塊A的三維滲透率屬性模型

2.2 一維卷積網絡模型屬性預測模型

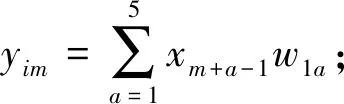
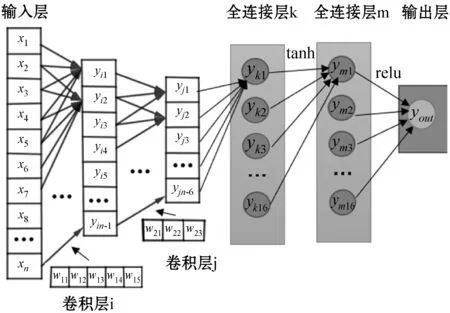
圖10 一維卷積神經網絡結構設計圖

網絡模型由兩層一維卷積層和兩層全連接層構成，采用初始學習率為0.001，動量為0.9的隨機梯度下降作為優化器訓練樣本數據，每隔一個訓練周期學習率自動下降50%，直到損失函數值達到穩定停止訓練，生成預測模型。一維卷積神經網絡結構設計偽代碼如下：

input=Input(size=n)

conv1=Conv1D(16,strides=1,kernel_size=5,activation=′relu′)

conv2=Conv2D(16,strides=1,kernel_size=3,activation=′relu′)

fl=Flatten()

fc1=FullyConnection(size=16,activation=′tanh′)

fc2=FullyConnection(size=16,activation=′relu′)

output=Output(size=1)

model.add(Input,conv1,conv2,fl,fc1,fc2,output)

以地質區域A的含水飽和度屬性為例，基于含水飽和度屬性值數據訓練一維卷積網絡模型。圖11為該樣本點屬性值分布直方圖。隨機抽取五個含水飽和度屬性樣本點的網格單元所在多個空間特征期望值和方差值如圖12所示。可以看出，在第20個子空間后空間特征變化不明顯，因此采用前20個子空間特征期望值作為深度學習網絡輸入，訓練一維卷積網絡獲得預測模型。

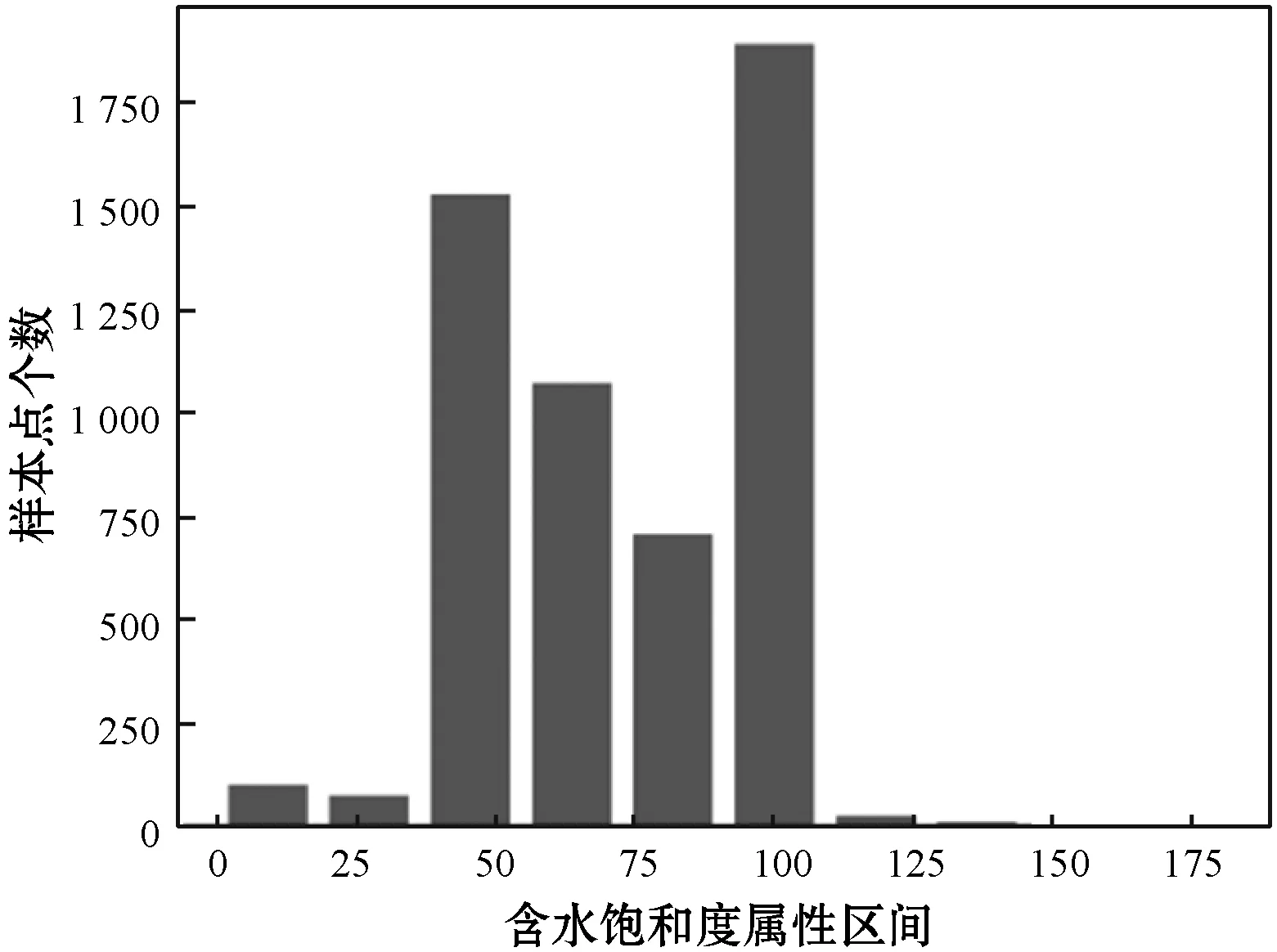
圖11 樣本飽和度屬性值分布直方圖

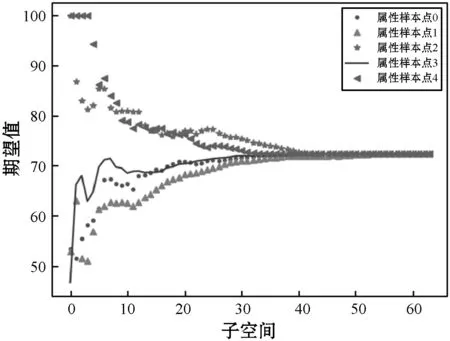
(a) 含水飽和度屬性樣本點所在多個空間期望值統計

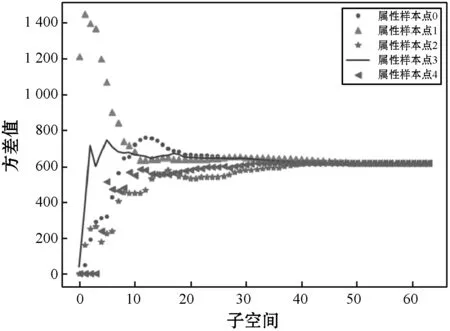
(b) 含水飽和度屬性樣本點所在多個空間方差值統計圖12 隨機5個含水飽和度屬性樣本點所在多個空間 期望值與方差值統計

同樣將含水飽和度屬性樣本點按照8∶2比例隨機分成訓練集和驗證集，經過模型訓練，在訓練集和驗證集中的含水飽和度實際屬性值與預測值的均方誤差較小，一維卷積網絡模型能夠較好地預測含水飽和度屬性值，如圖13所示。

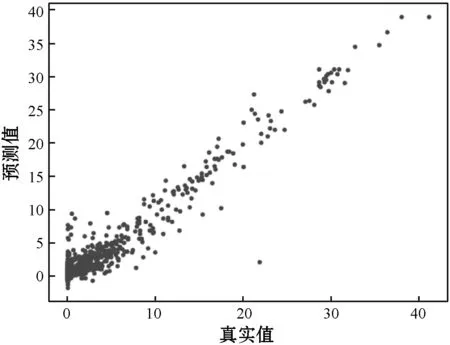
(a) 訓練集含水飽和度屬性預測值與真實值對比

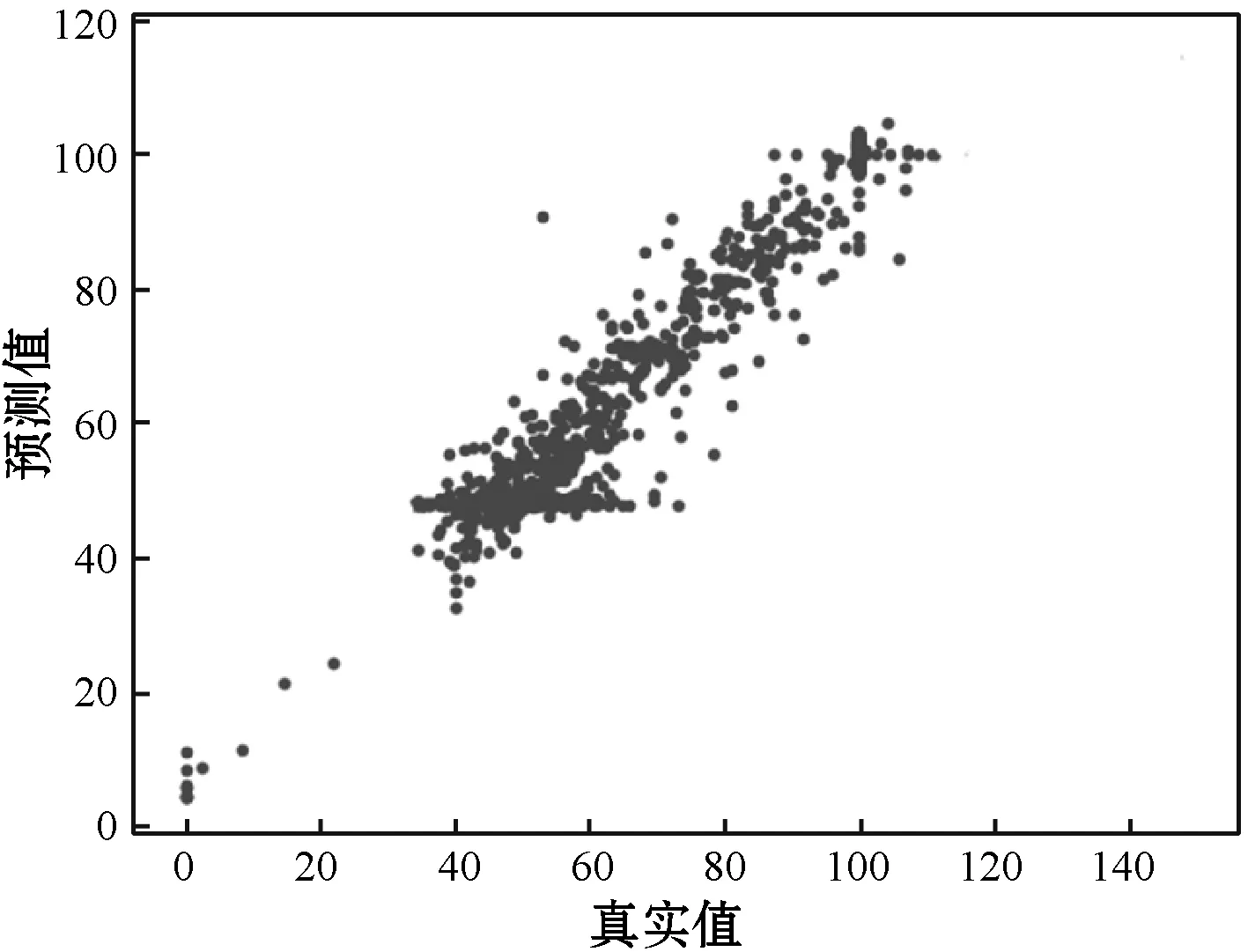
(b) 驗證集含水飽和度屬性預測值與真實值對比圖13 在訓練集與驗證集含水飽和度屬性預測值 與真實值對比

基于三維地質體構造模型，采用全連接網絡模型和一維卷積網絡模型建立屬性預測模型，屬性預測值分布趨勢具有一定的相似性，但也存在部分差異性。以地質區域A中的含水飽和度屬性為例，圖14展示了基于卷積網絡模型的預測效果圖，圖15展示采用全連接網絡的屬性預測效果圖，從三維可視化模型可見兩種模型預測結果具有明顯相似性。

圖14 基于卷積網絡模型預測三維含水飽和度屬性模型

圖15 基于全連接網絡模型預測三維含水飽和度屬性模型

驗證三維地質模型預測結果，從地質儲層滲透率屬性訓練數據樣本中隨機抽取80%數據作為訓練集，20%數據作為驗證集，建立基于全連接網絡預測模型和一維卷積網絡預測模型，并與基于80%樣本數據插值算法預測模型結果進行對比。經過5次交叉驗證，在驗證集上預測值與真實值的均方根誤差值RMSE見表1。

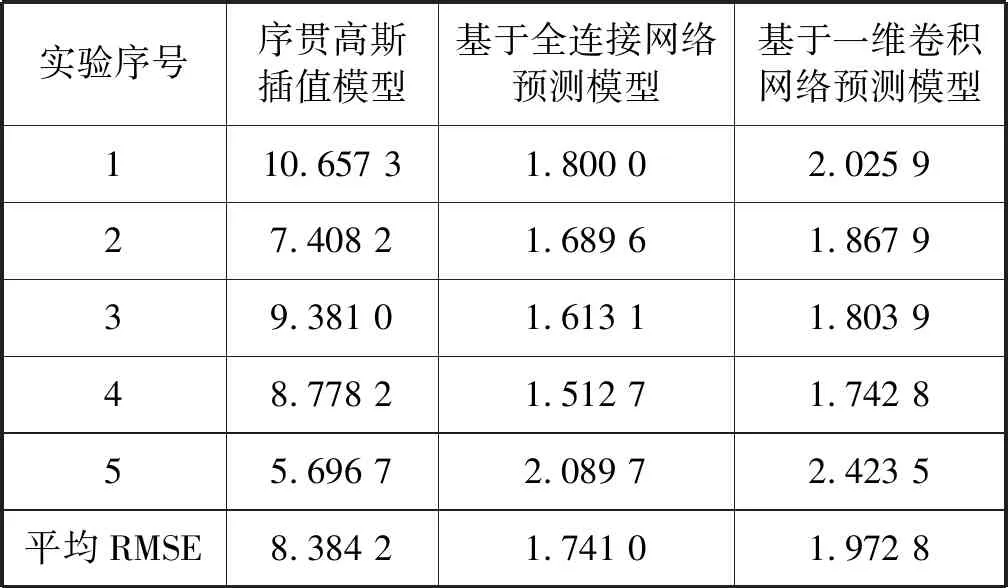
表1 滲透率屬性預測值與真實值的均方根誤差

由表1可見，基于全連接網絡和一維卷積網絡滲透率屬性預測值與真實值的均方根誤差比傳統序貫高斯插值小，傳統插值方法受到數據影響較大，少數數據不參與插值導致預測結果差異較大，而深度學習網絡預測結果以數據驅動為主，預測誤差較小，魯棒性較好。表1中第2組實驗中三種不同方法預測滲透率屬性預測值與真實值對比如圖16所示。

(a) 基于全連接網絡滲透率預測值與真實值對比

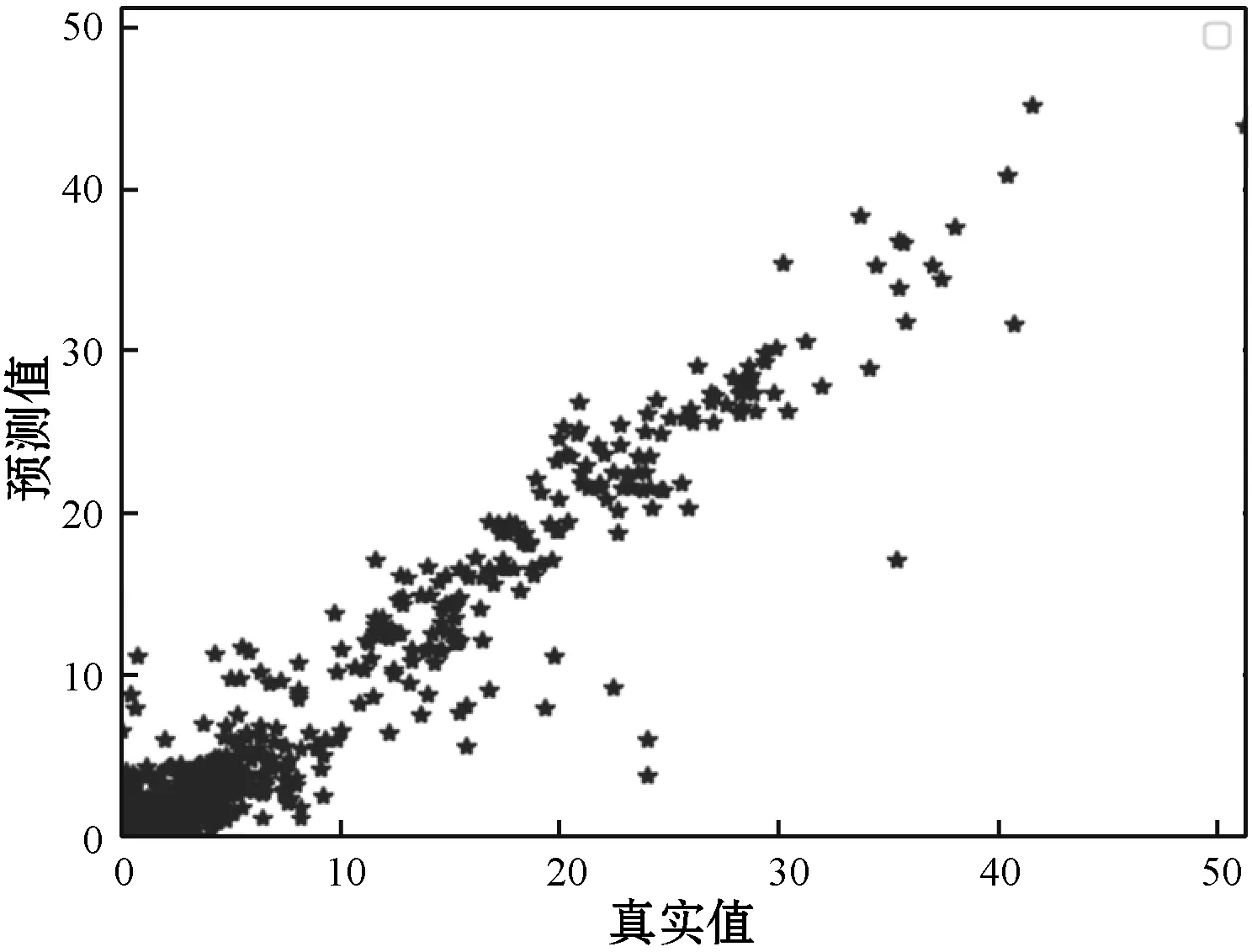
(b) 基于一維卷積網絡滲透率預測值和真實值對比

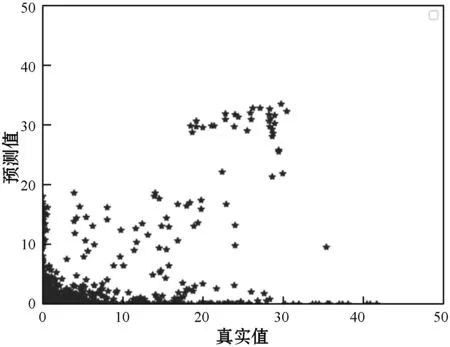
(c) 基于序貫高斯插值滲透率預測值與真實值對比圖16 三種預測模型滲透率屬性預測值與真實值對比

基于深度學習網絡，采用三維空間特征統計數據實現三維地質儲層屬性建模的方法。根據屬性在三維空間中的分布和統計特征，訓練深度學習網格模型得到屬性預測模型，很難判斷具體哪種學習網絡模型更具優勢，需結合空間統計數據分析，嘗試最合適網絡模型結果，這樣的嘗試和研究不同于傳統統計方法思路，具有一定的研究意義。基于三維地質模型，將應用三維卷積網絡模型預測地質屬性作為后續的一個研究方向，結合測井、地震等多種來源地質數據建立網絡模型的訓練樣本。采用三維卷積網絡模型分析三維空間中屬性關系預測屬性模型具有研究意義，但目前獲取適用于三維卷積網絡模型的訓練樣本數據具有一定的難度。本文提出的深度學習模型，能夠基于有限地質數據樣本研究地質儲層屬性在三維空間中的分布情況，建立三維地質儲層屬性預測模型。

3 結 語

本文嘗試采用深度學習方法解決地質儲層屬性預測和三維地質儲層屬性建模問題。基于三維構造模型，分析以網格單元為中心的一定范圍內空間特征統計結果，發現空間特征與網格單元屬性值之間的相關性，分別設計并訓練全連接網絡模型和卷積網絡模型，生成屬性預測模型，進而建立三維地質儲層屬性模型。兩種網絡建立三維屬性模型中屬性分布趨勢具有一定的相似性，基于有限數據驅動預測效果較好。結合深度學習方法解決三維屬性建模問題的方法研究具有一定應用價值。