基于改進多尺度排列熵的列車軸箱軸承診斷方法研究
李永健 宋 浩 劉吉華 張衛華 熊 慶
(1.五邑大學 軌道交通學院,廣東 江門 529020;2.西華大學 汽車測控與安全四川省重點實驗室,四川 成都 610039;3.西南交通大學 牽引動力國家重點實驗室,四川 成都 610031;4.西華大學 汽車與交通學院,四川 成都 610039)
軸箱軸承作為轉向架的關鍵零部件,將列車全部負荷經轉向架承受并傳遞至輪軌,使各車軸、車輪承重均勻分配。隨著列車速度不斷提高,軸承等主要零部件在高速工況下的服役環境變得更加惡劣,容易發生故障,為行車安全帶來重大隱患。因此,在列車復雜工況下及時檢測軸箱軸承的早期故障成為走行部狀態監測研究的熱點和難點。
列車實際運營中對軸箱軸承的主要檢測方式為車載軸溫報警裝置[1],軌邊聲學診斷系統(TADS)[2]以及基于振動的共振解調技術[3]。軸溫報警相對滯后而不能及時發現軸承早期故障,軌邊聲音診斷無法在列車運行過程中實時監測,基于振動信號的診斷技術由于克服了上述缺點而得到了廣泛應用。一般而言,振動信號的分析方法主要有基于峰值、有效值等指標的時域分析和基于傅里葉變換等的頻域分析。然而,由于轉速不恒定等因素引起振動信號呈現出較強的非線性和非平穩性,為了描述頻率隨時間的變化歷程,基于小波變換、希爾伯特黃變換以及溫格爾威利分布等的時頻分析方法應運而生[4-6]。這些方法由于各自的局限性,難免產生不穩定的結果。近年來,隨著非線性分析技術的不斷發展,不同的非線性特征提取方法被用于旋轉機械的故障診斷。熊慶等[7]研究了多重分形趨勢波動分析特征參數的敏感性和穩定性,并成功運用于滾動軸承的定量故障診斷;Yan等[8]將近似熵用于機械設備的健康監測;Li等[9]用層次模糊熵提取滾動軸承的故障信息,結合改進支持向量機分類器建立了智能故障診斷系統;Wu等[10]將多尺度排列熵應用于滾動軸承的故障診斷。
研究者Bandt等[11-12]基于相鄰值比較思想提出了排列熵技術,用以度量時間序列的復雜性參數,該方法尤其適用于處理含噪信號。隨后,巴基斯坦學者Aziz和Arif經由粗粒化處理建立了多尺度排列熵算法[13],較之于單一時間尺度下的排列熵,它能夠進一步挖掘蘊藏于時間序列中多個尺度下的信息,更加全面的表征系統的隨機性和復雜性,在腦電波信號的應用研究中取得了良好的效果[14]。此外,多尺度排列熵技術還被用來刻畫旋轉機械的健康狀態[10],實驗結果顯示,針對軸承的正常狀態以及不同組件的損傷,多尺度排列熵方法均能夠通過原始振動信號有效表征。然而該方法仍然存有缺陷:在粗粒化處理后,時間序列的長度會減少,而數據點的多少會影響熵值的計算精度以及穩定性,若信號中包含的數據點較少,熵值誤差會顯著增加,尤其當原始信號為短時的時間序列時尤為明顯。為了提高經典多尺度排列熵算法的穩定性和精度,本文從粗粒化過程著手,對傳統方法進行完善,提出了改進的多尺度排列熵。新方法有效解決了在處理較短的含噪信號時存在的熵值突變、精度低的問題,可以得到穩定性好、精度高的排列熵值。
因此,本文將改進的多尺度排列熵用于提取軸箱軸承復雜振動信號中隱含的故障特征信息,同時為了降低提取特征中的冗余信息和減小特征維數,馬氏距離[15]被用來選取包含最多敏感信息的故障特征。最后,與遺傳算法優化的支持向量機(GA-SVM)[16]相結合,對軸箱軸承的不同故障進行智能分類。實驗結果表明,本文提出的基于改進的多尺度排列熵、馬氏距離以及GA-SVM的故障診斷方法能夠有效對軸箱軸承不同位置故障進行精確識別。
1 改進多尺度排列熵
1.1 多尺度排列熵
多尺度排列熵將粗粒化過程與排列熵相結合,通過求取粗粒化時間序列的熵值得到不同時間尺度下的計算結果,可以挖掘到隱藏在時間序列中更豐富的特征信息,從而精確反映出系統的變化情況,比原始單一尺度[11]獲取更多的狀態量。多尺度排列熵技術的計算主要由兩部分組成,詳細過程如下[11-13]:

式中:τ為尺度因數,取正整數為小于或等于a的整數。
(2)對粗粒化后的時間序列計算排列熵PE值,即可得到多尺度排列熵MPE

式中:m為嵌入維數;δ為時延參數。
在應用研究中,由上述2個步驟計算的多個尺度下的PE值雖然效果良好,但是依然存在缺陷:①在粗粒化過程中,對每一數據點的處理并非完全一致,即MPE不是對稱的,這會導致PE值突變。如尺度因數取3時,其粗粒化過程見圖1。理想情況下x3和x4與x2和x3處的計算模式應完全相同,但是從圖1中發現x1、x2、x3與x4、x5、x6于x3處斷開,造成x3與x4存在斷點而PE值不穩定。②求取排列熵時信號的數據點越多結果越穩定,然而多尺度分析會降低時間序列的長度,隨著尺度因數的增大,用于計算PE的信號長度越短,這樣會不斷增加熵值誤差,使得對系統的表征精確性降低。

圖1 尺度因子等于3時的MPE過程示意
1.2 改進多尺度排列熵(MMPE)
為了完善和提高傳統多尺度排列熵的性能,本文從粗粒化步驟入手,建立改進多尺度排列熵。仍然以尺度因數3為例(見圖2),區別于原有算法的是新方法中同一時間尺度τ下,經粗粒化處理后可獲得τ組時間序列,從而解決“斷點”處的突變問題,而經典算法中只有一組時間序列。數學過程為:
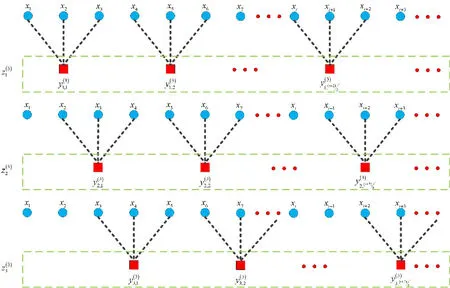
圖2 尺度因子等于3時的MMPE方法示意
(1)對給定信號以改進粗粒化過程進行處理,得到τ組新的時間序列

(2)對于每一組新的粗粒化時間序列z(τ)i|(i=1,2,…,τ),求取它的PE值,然后計算τ個時間序列熵值的平均值,即可得到時間尺度τ下的排列熵,具體為

(4)MMPE的熵值大小實則是系統內在變化的一種外在表現,由系統產生的信號說明了其本身的隨機性和復雜性,熵值越小表明信號越規則,反之則說明系統較無序和雜亂。
2 MMPE和MPE算法比較分析
2.1 參數選擇
由多尺度排列熵的定義可知,在計算時需要設置4個參數:N、m、τ、δ。一般而言,嵌入維數取值范圍為3≤m≤7,當m≤2時,由于重構時間序列中蘊含的重要信息量太少,將會使算法的有效性大打折扣;而m值過高,又會增加計算量,且對時間序列的細微變化也難以描述[8],鑒于此該參數取m=4。此外被分析信號數據點的多少將會影響PE值的精度,信號越長熵值精度越高,然而太多的數據點在計算時會更耗時,若數據點太少則不能精確反映系統的狀態變化,文獻[17]建議取N≥5m!,此處取N=2 048。由于時延參數對最終結果的影響微乎其微,為了方便求解,給定δ=1。根據研究需要,時間尺度選擇τ=20。
2.2 仿真對比分析
為了說明MMPE的優點,通過仿真信號高斯白噪聲和1/f噪聲進行分析研究。2種信號長度均為5 000個數據點,時域圖和頻譜圖見圖3。從圖3中可知,高斯白噪聲比1/f噪聲更加具有復雜性。然后用MMPE和MPE算法分別求得2種信號的排列熵值,見圖4,從圖4中可以看出,在不同尺度下MMPE方法所求熵值較之MPE方法穩定;另一方面隨著尺度因數的增大,排列熵值在單調遞減。為了分析改進方法的誤差,分別對高斯白噪聲和1/f信號各取100個樣本,求取尺度1~20下的PE,計算每一尺度的熵值誤差,見圖5。通過分析圖5可以證實,從尺度1~20下改進算法比傳統的MPE技術得到更加精確結果,誤差小且抑制了突變的發生,由此證明MMPE技術具有良好的穩定性。

圖3 高斯白噪聲和1/f噪聲時域與頻譜

圖4 高斯白噪聲和1/f噪聲排列熵

圖5 高斯白噪聲和1/f噪聲排列熵誤差
3 損傷檢測方法
軸箱軸承是列車上最關鍵的旋轉零部件之一,一旦軸承內部有組件發生缺陷,都會產生不同程度的振動脈沖信號。由于軸箱處于復雜多變的運行環境,各個部件的頻率容易調制,引起加速度信號表現出相當的復雜性,而且在高速、低速和加減速時軸承的振動幅值、頻率皆呈現出強烈的非穩定性。此處基于非線性的MMPE技術分析非穩定的軸箱信號,計算不同時間尺度下的排列熵信息以表征軸承的健康狀態。然而,所有尺度下的熵特征既蘊含了關鍵的軸承狀態信息,同時大量的不相關信息也被一并提取。如果所有的熵值作為診斷向量,將會導致識別精度的下降而且更加耗時。為了提高效率和識別率,對特征向量加以篩選。馬氏距離[15]作為最常用的特征選擇方法之一,在諸多領域的研究中被廣泛采用。顧名思義,該方法主要以不同特征間的馬氏距離對所有特征進行排序,進而評估不同時間尺度下的熵值對軸承狀態的區分能力。因此,本文通過馬氏距離算法選取區分性能最優的熵特征為診斷向量,結合經典的SVM分類識別技術,對軸箱軸承實現智能化的損傷檢測。主要分為4個步驟:
Step1應用MMPE方法計算不同健康狀態下的多尺度排列熵值。根據本文2.1節中分析給定相關參數:N=2 048,δ=1,m=4,τ=20。
Step2通過馬氏距離算法評估所有時間尺度下的熵特征,選取排序最前的5個熵值重新組建診斷向量。
Step3在新特征向量中,任意選取50%樣本用于訓練分類模型,剩余50%樣本進行分類測試。
Step4由訓練樣本得到SVM分類方法的關鍵參數,由測試樣本完成軸承不同健康狀態的智能分類,通過診斷精度識別軸承的運行狀態。
4 試驗驗證
為了對文中提出的故障診斷方法進行有效性驗證,借助于客車檢修基地的輪對跑合試驗臺完成了不同健康狀態軸箱軸承的跑合試驗以便采集加速度數據。試驗平臺結構示意見圖6(a):整個輪對由安裝于下方的摩擦輪驅動,輪對兩側分別安裝2個軸箱軸承,為了便于比較,一個軸承為損傷狀態,而另一個保持健康狀態,輪對由相應的夾具固定,靜態力加載通過升高下方整個基座來實現,試驗時施加20 k N的徑向力;試驗裝置實物圖見圖6(b)。

圖6 實驗平臺結構示意及實物
對于軸箱軸承而言,采集信號時最好將傳感器置于外圈承載區,因為此處產生的沖擊更強烈。從圖6可以發現,該試驗裝置的承載區處于軸箱12 點鐘位置,但是該位置被用來加載靜態力。因此為了盡可能采集到包含重要信息的加速度信號,傳感器應安裝在接近承載區位置,見圖7。

圖7 傳感器安裝位置
試驗用軸承為客車軸箱軸承,是一種型號為NJ(P)3226X1的雙列圓柱軸承。分別在軸承的內圈、滾動體和外圈上通過電火花方法產生劃痕缺陷,損傷尺寸寬度為0.1 mm、深度為0.43 mm。試驗過程中,車輪轉速恒定為230 r/min,收集數據時選用25.6 k Hz的采樣率。不同狀態下軸箱振動信號時域圖見圖8,不管振動幅值還是沖擊周期,從圖8中無法判斷軸承的運行狀態,這是由軸箱運行工況的復雜性所致。
首先利用實測信號評估該方法對干擾噪聲的魯棒性。以健康狀態的加速度信號為基礎,分別添加大小各異的高斯白噪聲,使得合成信號的信噪比SNR依此為20、25、30、35 d B。然后對不同信噪比的新信號求取多尺度熵值,曲線結果見圖9。從圖9中可以發現,在大部分時間尺度下排列熵值并未發生突變,呈現出了良好的穩定性和一致性,說明MMPE技術對噪聲具有優越的抗變換性。

圖8 不同健康狀態軸箱軸承的時域波形

圖9 正常狀態軸承信號在不同信噪比SNR下的排列熵
其次,對健康狀態以及3種損傷(內圈、滾子和外圈)的加速度信號應用MMPE方法完成熵值提取。分別計算不同健康狀態下的多尺度熵值,并繪制曲線,見圖10。通過觀察可發現,外圈損傷的熵特征值在不同尺度下呈現出不斷上升后略微下降的趨勢,而健康狀態和另外2種損傷均表現為先遞減、遞增和下降的特征,由此不僅充分體現了軸承運行工況的復雜性,而且表明原始單一尺度下的熵值在刻畫軸承運行狀態時存在的局限性。

圖10 不同狀態軸箱軸承的排列熵
最后,將正常狀態和其他3種故障狀態軸承分別取30個樣本,合計120個樣本。對每個樣本提取MMPE熵值,建立原始特征集。將所提取的特征集使用馬氏距離算法進行排序,最能表征不同軸承故障狀態的特征向量排在前面,評估后最前面的5組熵值被用來重新組建智能故障診斷的新向量,其中,任意15個樣本用來訓練分類模型,剩余15個樣本進行識別測試。經過遺傳算法優化的SVM分類器(核函數為徑向基函數)進行訓練、測試,最終得到的故障分類結果見表1。

表1 本文方法測試分類精度 %
從表1可知,文中提出的故障診斷方法對不同類型故障的識別率達到了98.33%,除了一個內圈樣本被誤分類到滾動體故障外,其余樣本均被正確識別,充分證明了該方法在軸箱軸承診斷中的有效性。
為了與傳統的排列熵算法對比,現對相同的120個振動信號樣本求取MPE值,參數設置與MMPE方法一致,從提取的原始特征集中選擇前5個尺度下的故障特征進行SVM分類器的訓練和測試,參數設定與前文一樣。測試結果見表2,識別率下降到了95%,有2個正常狀態被分到了外圈故障,一個滾子故障被誤分為內圈故障。該比較結果說明了文中改進方法的優越性。

表2 MPE方法提取狀態特征測試分類精度 %
最后,我們考慮不使用馬氏距離方法進行特征優選,而是隨機選取5個不同尺度下的MMPE故障特征向量作為診斷特征集。隨機選擇的5個尺度分別為1、5、7、10、12,在與前文相同參數設置下,將訓練和測試樣本輸入SVM分類器。最終識別結果見表3,測試樣本中有2個滾子故障的樣本被分類到內圈故障,此時正確識別率為96.67%,較之文中所提方法低1.66%,表明使用馬氏距離算法進行特征優選的必要性。

表3 隨機選取狀態特征測試分類精度 %
5 結束語
軸箱軸承在列車運行過程中發生故障時,處于復雜服役環境下會表現出多種隨機性和動力學行為。本文對基于非線性的MPE方法做了必要改進,提出了MMPE方法。與2種仿真信號進行比較,得出了更為穩定的結果。隨后將該方法應用于客車軸箱軸承的實驗數據特征提取,結合馬氏距離和基于遺傳算法優化的支持矢量機,建立新的軸箱軸承故障診斷方法,實現了故障的正確分類。通過比較分析發現文中所用方法的優越性,為智能化故障診斷提供了一種新的思路。筆者后續將會繼續對基于熵的非線性分析方法進行深入研究,以期能夠運用于工程實際,保障列車安全運行。

