隧道圍巖變形的時空特性研究

于富才，張頂立，王文波，王 凱, 李倩倩

(1. 北京交通大學 城市地下工程教育部重點實驗室，北京 100044; 2. 北京市安全生產科學技術研究院，北京 101100；3. 中鐵建設集團有限公司, 北京 100131; 4. 北京中鐵建物資貿易有限公司， 北京 100039 5. 北京城市快軌建設管理有限公司, 北京 100027)

隧道開挖擾動將破壞地層的初始應力狀態，在應力重平衡過程中，將伴隨圍巖變形發展甚至發生結構破壞現象。而各類支護結構適時介入可以改變應力轉移的方向，協助隧道結構體系盡快實現二次平衡。可見，在力學上，隧道結構的構建過程即為隧道支護——圍巖體系在一定空間范圍和時間尺度內的應力再平衡過程。隧道圍巖變形具有科學性、及時性、可靠性和便捷性的特點，目前已經成為表征支護—圍巖體系時空特性的最直觀指標[1]。

收斂約束法是隧道結構初期設計的一種基本工具，包括圍巖特性曲線、支護特性曲線和縱向變形曲線三項基本內容[2-3]。其中，縱向變形曲線(以下簡稱LDP)能夠反映隧道變形的時空效應，可有效指導支護結構剛度、強度及施作時機的確定，國內外學者就此已開展了大量的研究工作并取得了許多有益的成果。基于數值模擬結果，Panet等[4]擬合了掌子面后方圍巖變形與距掌子面距離的函數關系，隨后，經Panet[5]修正后得到了彈性和彈塑性分析的統一函數形式；González-Nicieza等[6]考慮兩種非圓斷面的影響，得到了包含角度和埋深參數的洞壁圍巖徑向位移的LDP修正公式；Unlu等[7]在隧道彈性圍巖LDP擬合公式中考慮了泊松比的影響；Vlachopoulos等[8]采用二維軸對稱模型分析理想彈塑性圍巖中圓形隧道的變形特性，建立了最大塑性區半徑與LDP的函數關系(以下稱Vlachopoulos公式)；隨后，Alejano等[9]將這一公式推廣到了應變軟化巖體中；吳順川等[10]根據三維數值模擬結果，建立了不同BQ(巖體基本質量定量分級標準)水平和不同埋深條件下LDP的擬合公式。基于明塔姆電力隧道(Mingtam Power Cavern)現場實測數據，提出了隧道徑向變形與距掌子面距離關系的經驗擬合公式[11]；李煜舲等[12]提出了新的掘進效應函數并闡明了各參數的適用范圍及物理意義。張常光等[13]對等值應力場下圓形隧道位移釋放系數的求取方法進行了系統的比較分析，證明了Vlachopoulos公式的合理性。但是，既往研究對隧道圍巖變形的空間分布和演化規律的分析仍不夠系統，各類隧道LDP的計算公式在實際應用中仍存在諸多限制，如彈性或彈塑性圍巖中圓形隧道的計算公式不能考慮非圓斷面的影響，彈性圍巖中兩種概化非圓斷面隧道的計算公式不能考慮復雜圍巖特性和實際隧道斷面的影響，而根據單一隧道監測數據獲得的擬合公式則僅適用于特定工程。

因此，采用三維有限差分方法，從隧道洞周圍巖變形和沿隧道軸向的圍巖縱向變形兩個方面，對自重壓力場下理想彈塑性圍巖中未支護隧道圍巖變形的時空特性進行分析，并采用擬合分析方法獲得圍巖縱向變形曲線的預測公式，為指導工程現場監測、實現動態化設計與施工提供重要依據。

1 數值模擬方案

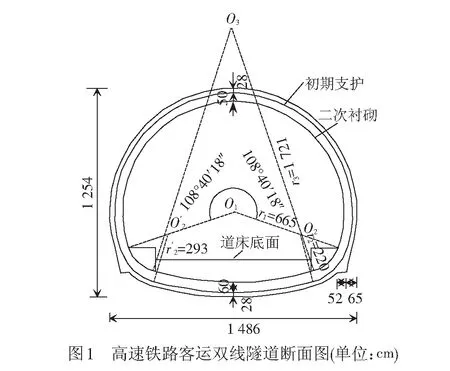
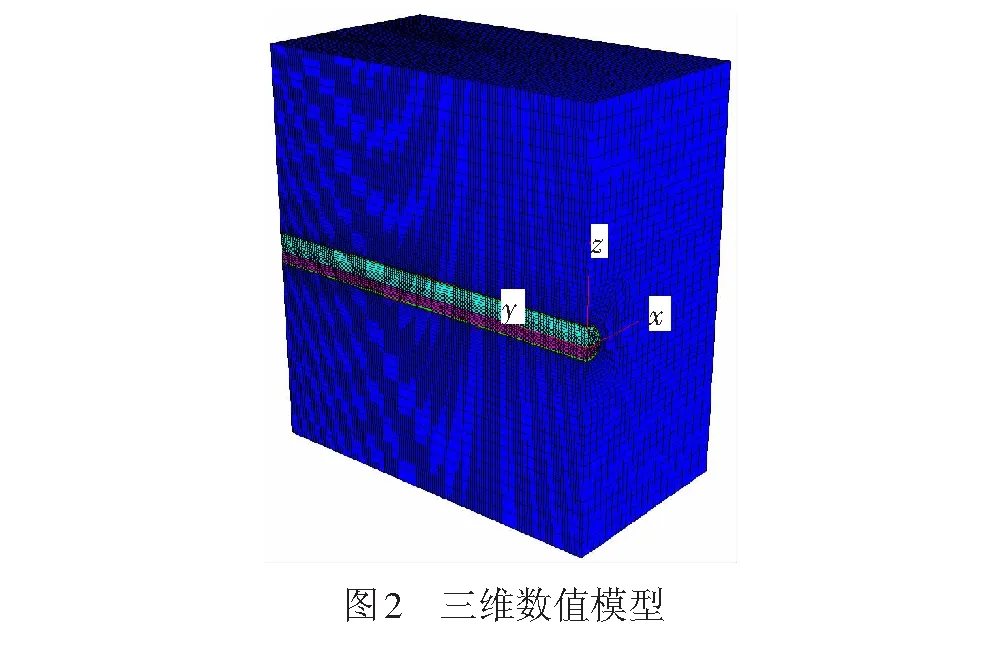
根據相關研究成果[14-15]，隧道圍巖變形遵循“變形加速→急劇變形→緩慢變形→變形穩定”的共性演化規律，與圍巖力學性質、支護結構力學特性和施作時機、開挖方案等因素無關，說明開挖方案和支護結構僅能通過控制圍巖的應力釋放降低圍巖的變形速率和變形量，不能改變基本的圍巖變形規律。因此，基于我國鐵路行業的發展特點，參考文獻[16]，以速度350 km/h高速鐵路客運雙線隧道為研究對象,見圖1，采用有限差分程序FLAC3D對無支護隧道圍巖變形的時空特性進行分析。為提高計算效率，建立以O1O3為對稱軸的三維分析模型,見圖2，模型尺寸為140 m×77.43 m×152.54 m(長度×高度×寬度)，均大于10倍隧道半跨寬度，模型包含184 851個節點和172 480個單元。三維模型的6個邊界均在法向方向采用位移約束，不同埋深條件通過在邊界施加的法向應力進行模擬。采用逐步開挖法[8]分析開挖擾動下圍巖變形的動態特征，開挖進尺為1 m。

采用二維模型計算圍巖最終變形和塑性區半徑，模型共包含2 622個節點和1 232個單元，有限差分網格劃分與三維模型的xz截面一致。

圍巖采用理想彈塑性本構模型和Mohr-coulomb屈服準則，地層側壓力系數為1，物理力學參數取值與文獻[8]一致，并基于Hoek方法[17]計算等效黏聚力c和等效內摩擦角φ,見表1。

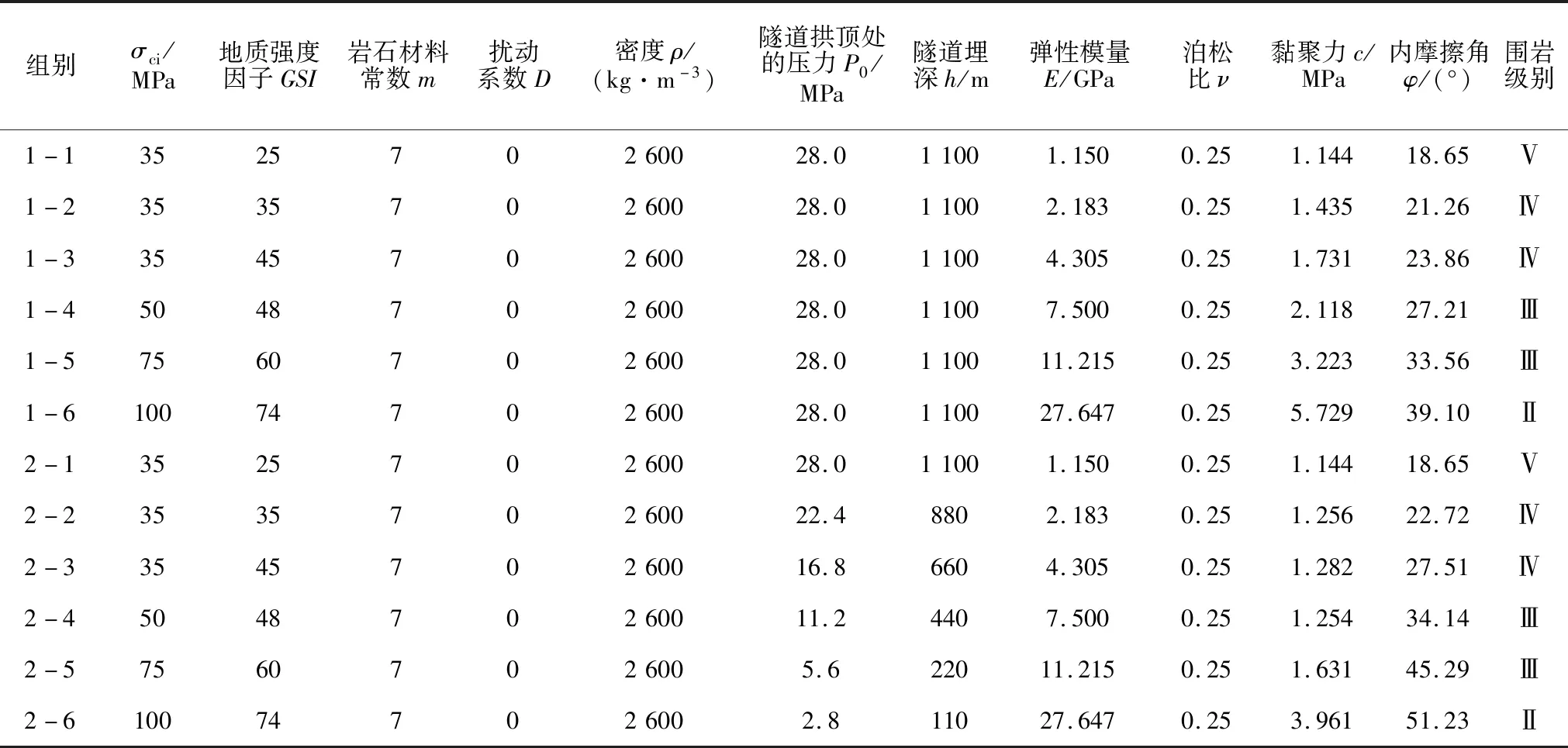
表1 圍巖物理力學參數

注：① 組別2-1與組別1-1的參數取值完全一致，后文將不做重復分析；② 表中，σci為完整巖石的單軸抗壓強度。

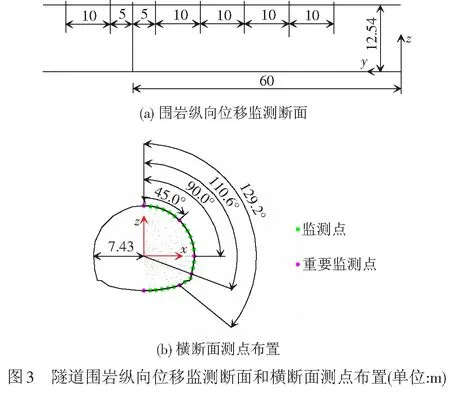
實時監測三維模型中距掌子面不同距離的8個斷面的圍巖位移(見圖3(a))，每個斷面包含25個監測節點(見圖3(b))。通過分析各斷面不同測點處的徑向位移(分別指向各弧線圓心，折線段指向圓心O1)，總結未支護隧道圍巖變形的分布特點及動態演化特征，確定隧道工程現場監測的重要監測點。隨后對隧道圍巖關鍵位置處LDP進行擬合分析，構建隧道圍巖縱向變形的預測公式。

2 隧道洞周圍巖變形的時空特性

2.1 圍巖變形的空間分布特點

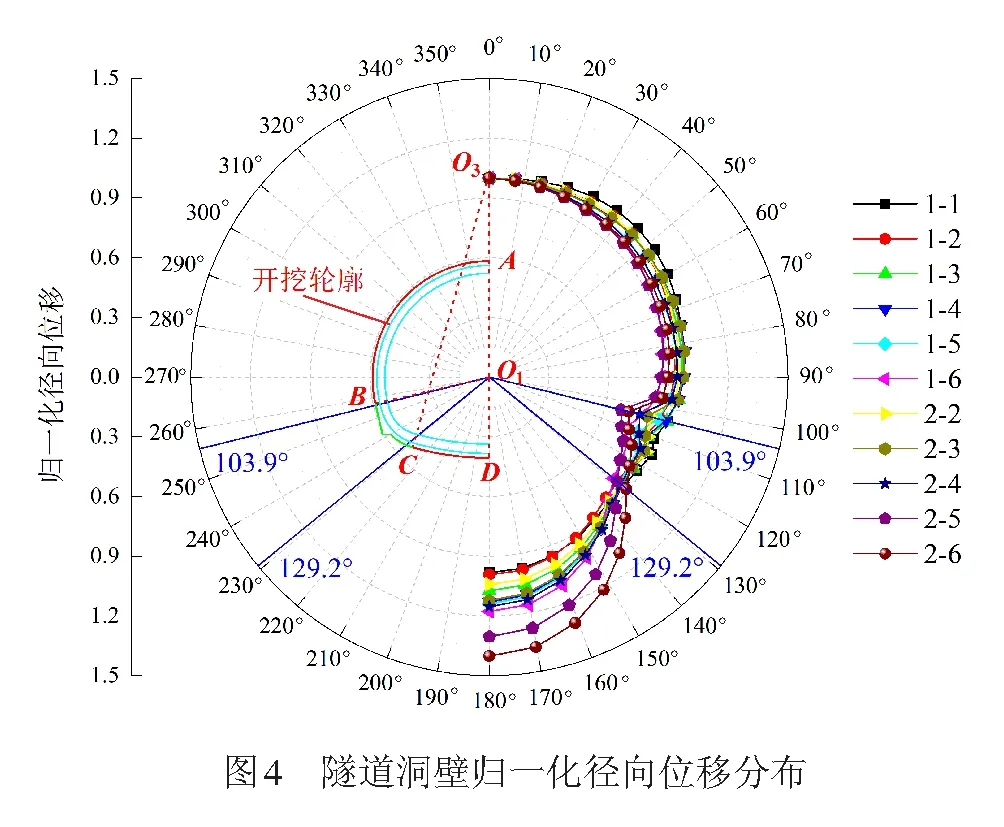
利用二維模型計算隧道斷面測點的最終徑向位移和等效塑性半徑，見表2。結果表明，歸一化塑性半徑越大，圍巖最終徑向位移越大。根據隧道洞壁歸一化徑向位移的空間分布情況(見圖4)，隧道斷面非圓效應隨塑性半徑的增大逐漸減弱，圍巖位移的空間分布趨于均勻。其中，圓弧O1AB和圓弧O3CD之間(即BC段)斷面線型較為復雜，應力集中將導致B、C兩點之間(即103.9°～129.2°范圍內)圍巖變形向下波動較大，而圓弧O1AB和圓弧O3CD段圍巖變形則相對均勻。

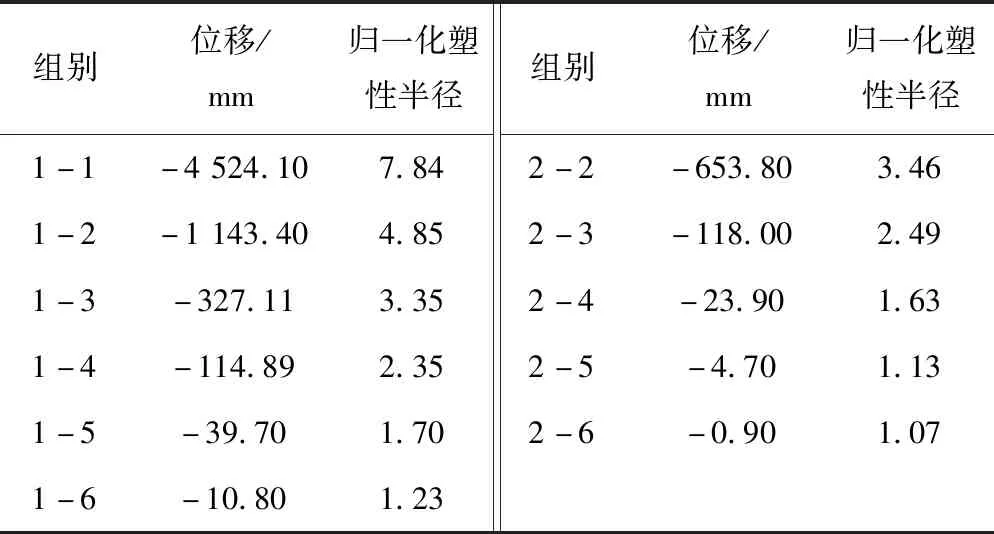
表2 二維平面模型計算結果

注：① 歸一化塑性半經=等效塑性半經/隧道半跨寬度，等效塑性半徑根據面積等效原則計算；② 文中絕對位置值的正負號僅表示位移方向，指向隧道內部為負，指向隧道外部為正。

根據圍巖變形空間分布特點，分析拱頂(0°)、拱肩(45°)、拱腰(90°)、拱腳(110.6°和129.2°)和拱底(180°)6個典型測點的位移計算結果，見表3。結果表明，拱腳位置的圍巖徑向位移最小，而拱底位置最大，且最大值和拱頂位移的比值與塑性半徑成反比，比值最大為1.40，因此，施工中應密切關注拱底隆起，盡早施做仰拱結構并及時回填，防止圍巖破壞，保證施工進度。由于61%的隧道施工事故為圍巖坍塌和冒頂片幫[18]，施工中應重點監測道床底面以上圍巖變形(即拱頂、拱肩和拱腰位置)，與實際工程中常見的圍巖變形監測方案一致。由圖4、表3可知，圍巖位移在圓弧O1AB段的空間分布較為均勻，拱頂和拱肩位置的位移最大，且二者的比值在0.95～1.06之間，差異較小，因此，拱頂徑向位移是表征圍巖安全狀態的重要指標。

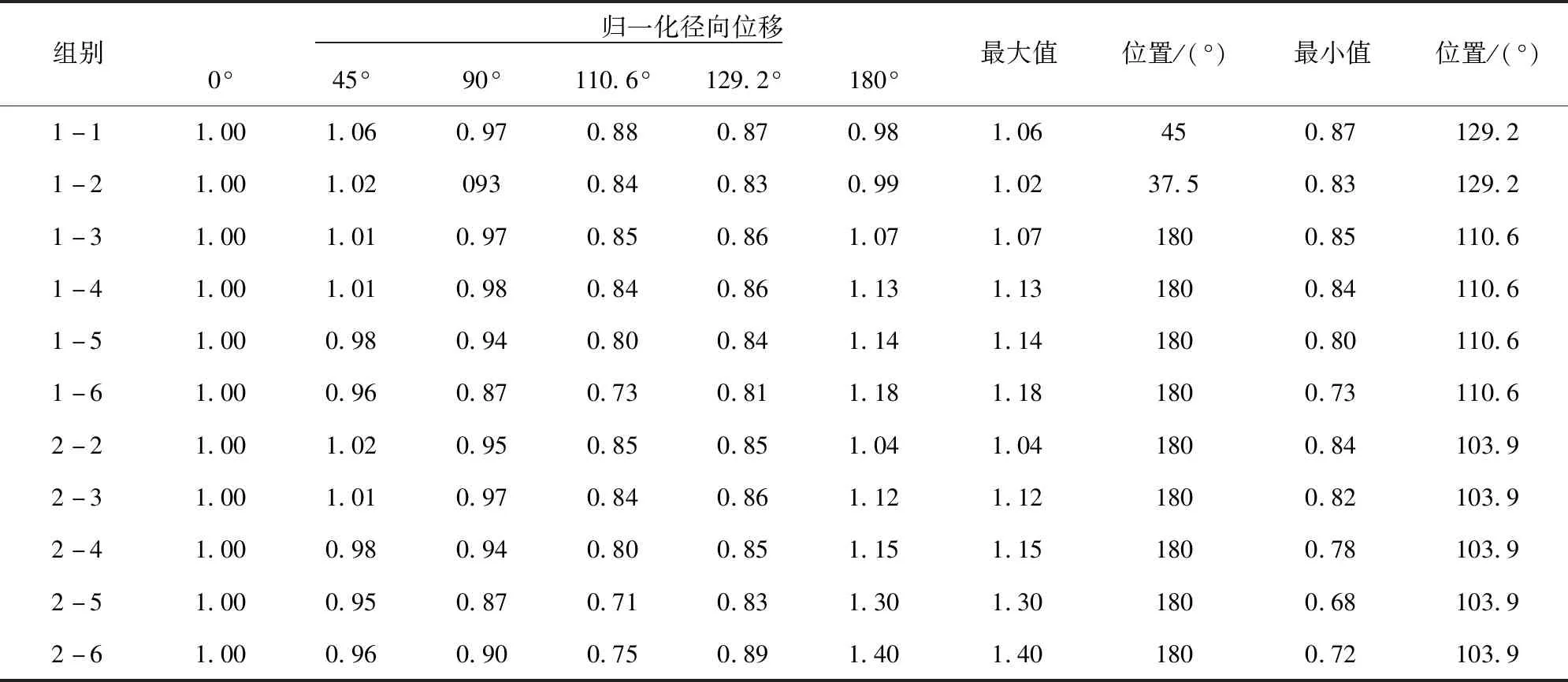
表3 隧道洞壁關鍵位置歸一化徑向位移計算結果

注：歸一化徑向位移=不同位置最終徑向位移/拱頂最終徑向位移。

2.2 圍巖變形的演化規律

不同開挖階段的圍巖徑向位移演化特征見圖5，圍巖徑向位移計算結果見表4。歸一化塑性半經以組別1-2、2-3、1-5和2-5為例，綜合分析可知：

(1) 未開挖到監測斷面時，掌子面的約束效應顯著，圍巖變形較小，斷面的非圓效應影響較小，圍巖位移的空間分布較為均勻；開挖面到達監測斷面以后，圍巖變形快速增加，且以后各階段圍巖變形分布曲線呈現自相似特性。

(2) 根據組別2-3計算結果，在距離掌子面15 m處，圍巖徑向位移最大值出現在拱頂，在掌子面距監測斷面較近直至到達或超越監測斷面后，圍巖徑向位移最大值均出現在拱底，而最小值則始終位于B、C兩點之間；在弧線O1AB段，圍巖徑向位移最大值均出現在拱頂或拱肩位置，且二者差異不大，符合圍巖變形的空間分布特點，說明掌子面后方各階段圍巖變形的空間分布特點基本一致，因此，掌子面后方圍巖變形空間分布曲線具有自相似特征。

綜上所述，在自重應力條件下，道床底板以上區域的圍巖變形分布較為均勻，相對于此，隧道拱底隆起則將隨圍巖性質的增強而增大。結合圍巖變形隨時間發展的自相似特性，以隧道拱頂的圍巖變形規律表征隧道結構體系的穩定性是合理的。但是，由于實際工程的地層應力和圍巖物理力學參數往往是復雜多變的，分析時應結合多個位置的監測數據，反分析地層的實際條件，確定合理的處置措施和時機。

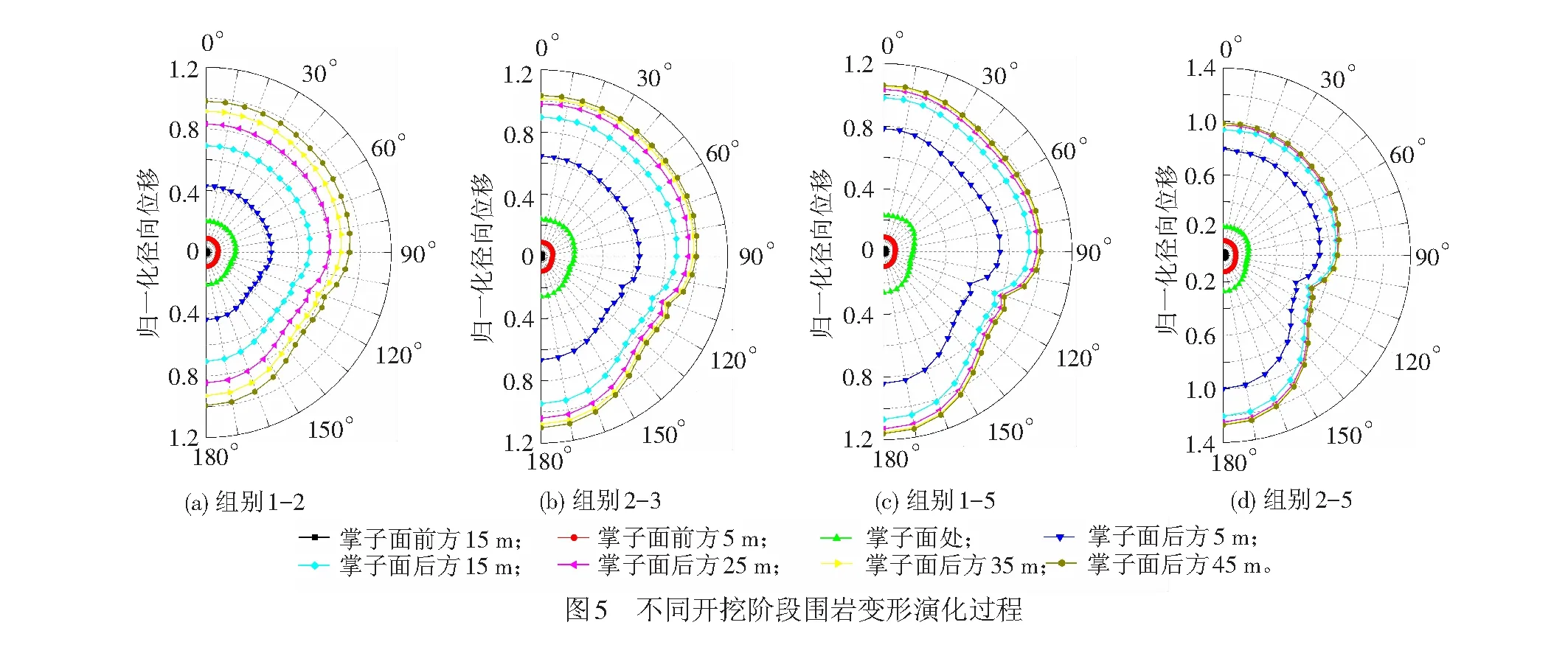
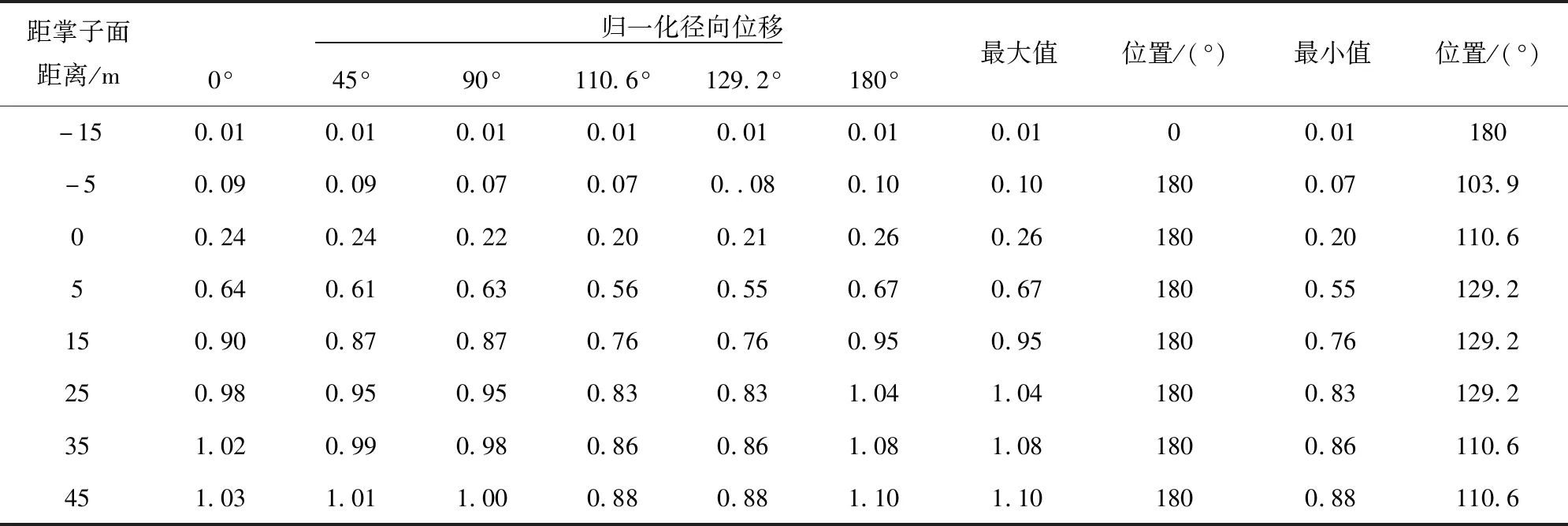
表4 不同開挖階段圍巖變形計算結果(組別2-3)

注：2.2節及后文中，歸一化徑向位移=不同開挖階段不同位置徑向位移/拱頂最終徑向位移。

3 隧道拱頂圍巖的縱向變形曲線

3.1 拱頂圍巖縱向變形的擬合分析

根據上述分析結果，隧道施工中的坍塌和冒頂片幫安全事故主要集中在弧線O1AB段(見圖4)，而拱頂和拱肩是安全風險最集中的位置，且拱肩變形與拱頂十分接近，因此，可將拱頂變形作為評價隧道安全狀態的關鍵指標進行擬合分析。

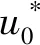
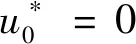
( 1 )

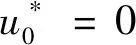
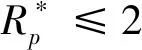
( 2 )

根據分析，在掌子面前方，由于核心土約束效應顯著，隧道斷面非圓效應較弱，參數h取恒定值為1.25，即當歸一化的距掌子面距離X*≤0時，函數的表達式為

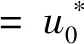
( 3 )

表5 參數擬合結果

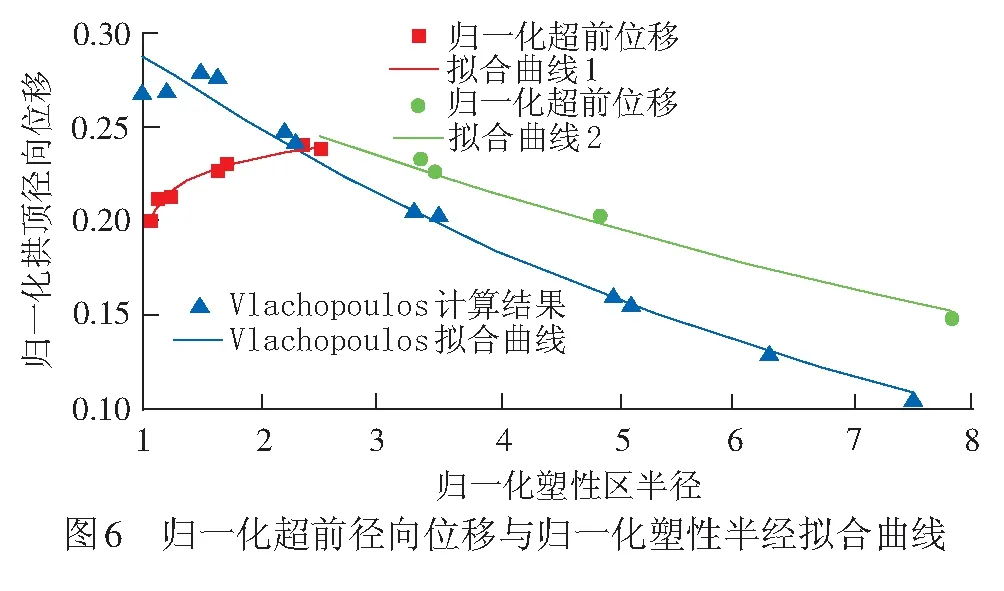
在掌子面后方，即X*≥0時，采用式( 4 )進行擬合，擬合結果見圖7、表6，相關系數均大于0.97，擬合效果良好，表達式為

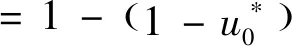
( 4 )

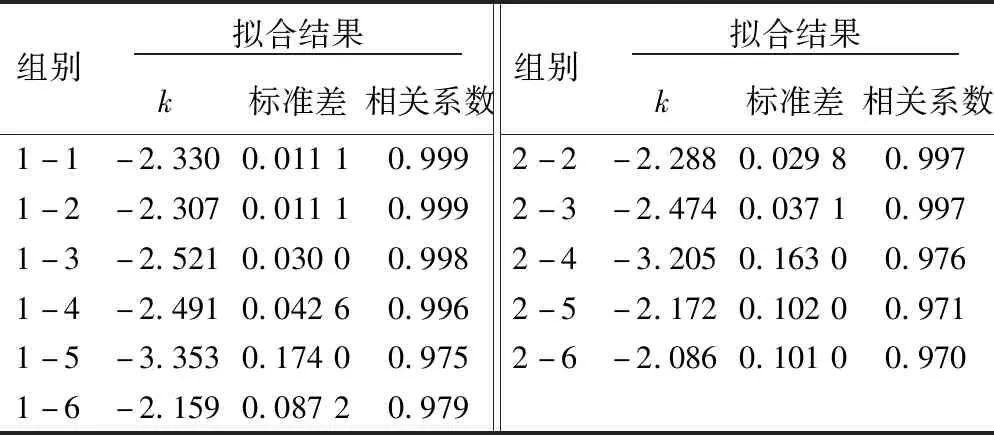
表6 擬合參數取值

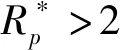
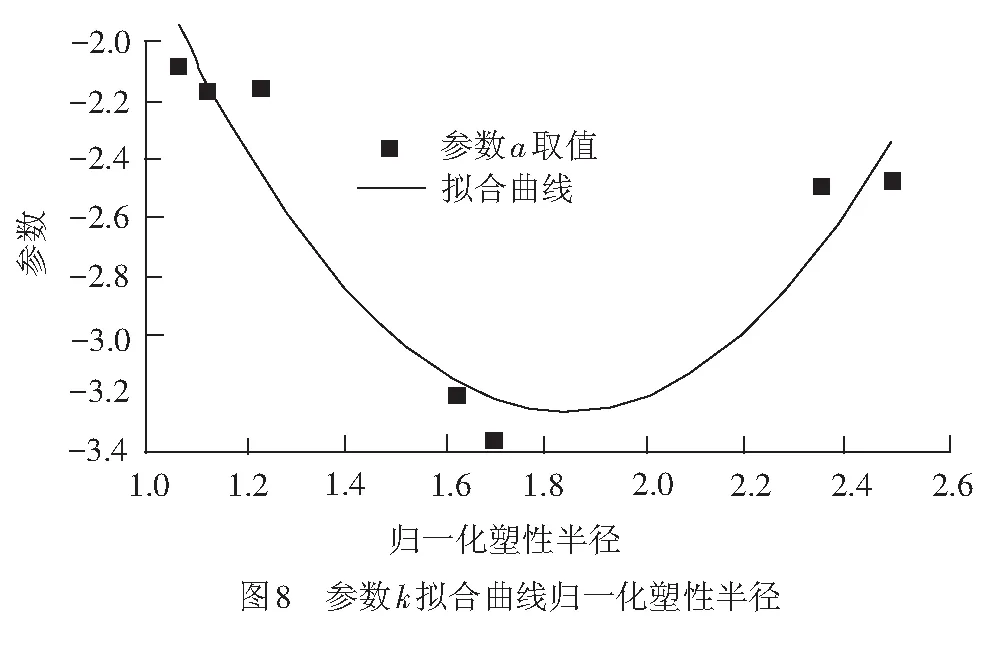
k=-2.362

( 5 )

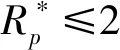
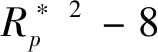
( 6 )

式( 1 )～式( 6 )的計算結果和數值模擬計算結果的吻合較好(見圖9)，說明隧道拱頂LDP預測公式適用于速度350 km/h高速鐵路客運專線隧道，可為類似隧道圍巖安全控制提供科學依據。

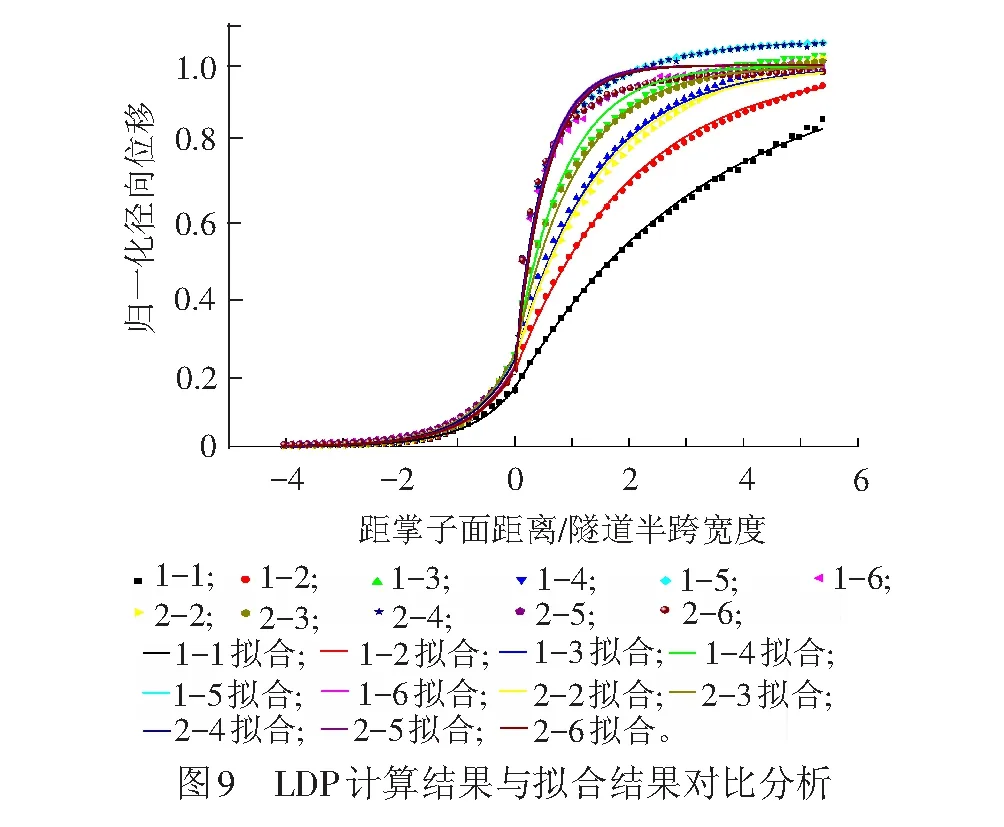
表7 參數擬合結果

3.2 拱頂圍巖縱向變形曲線對比分析

Vlachopoulos基于對等值地應力下巖質圓形隧道的數值計算結果，提出了LDP與圍巖塑性區最大半徑關系的擬合公式，其考慮了埋深和圍巖力學性質的影響，具有良好的適用性[13]。任選3組新工況進行數值分析，見表8，通過對比式( 1 )～式( 6 )計算結果和Vlachopoulos公式計算結果的計算誤差，驗證所提出公式預測高速鐵路隧道拱頂LDP的適用性。

表8 圍巖物理力學參數

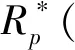
( 7 )

( 8 )

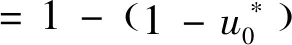
( 9 )

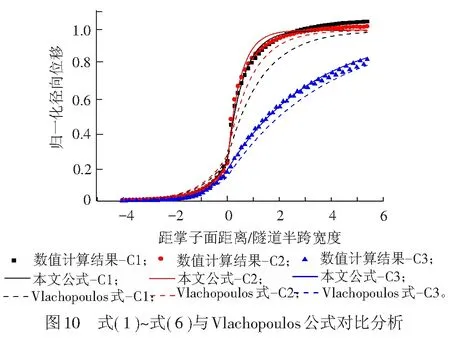
根據計算結果見圖10，式( 1 )～式( 6 )計算結果與數值模擬結果的差異明顯小于Vlachopoulos公式，證明了式( 1 )～式( 6 )能夠更好的預測高速鐵路隧道拱頂LDP，對隧道圍巖變形預測分析、支護措施設計和施工安全控制具有重要意義。

4 結論

采用數值模擬方法分析自重應力場下隧道圍巖變形的空間分布特點和演化規律，通過擬合分析提出適用于高速鐵路隧道的圍巖縱向變形計算公式，對實際工程具有重要的指導意義。

(1) 圍巖性質越好，隧道下部圍巖變形相對隧道上部越大，施工中應盡早施作仰拱結構或采取其它有效的控制措施；在隧道開挖邊界的兩個曲率變化關鍵點之間，圍巖變形最小；隧道上部圍巖變形分布較為均勻，最大值出現在拱頂或拱肩位置，拱頂徑向位移可作為評價隧道工程安全狀態的關鍵指標。

(2) 在掌子面前方，核心土的約束效應顯著，隧道斷面非圓效應較弱，位移分布較為均勻；在掌子面后方，圍巖變形快速增加，隧道斷面非圓效應顯著，但是各階段的變形分布呈現了明顯的自相似特征，說明隧道洞周各點的圍巖變形演化規律基本一致。

(3) 隧道斷面非圓效應隨圍巖塑性半經的增大逐漸減小，隧道拱頂LDP的預測公式為分段函數；通過任選的3種新工況與Vlachopoulos公式的計算結果進行對比分析，證明了所提出的高速鐵路隧道拱頂圍巖縱向變形預測公式的適用性良好。