反彎點(diǎn)求固結(jié)系數(shù)的數(shù)值方法

林麗萍，劉可定，賀建清，姚琪

反彎點(diǎn)求固結(jié)系數(shù)的數(shù)值方法

林麗萍1，劉可定1，賀建清2，姚琪2

(1. 湖南城建職業(yè)技術(shù)學(xué)院，湖南 湘潭 411101；2. 湖南科技大學(xué) 巖土工程穩(wěn)定控制與健康監(jiān)測(cè)省重點(diǎn)實(shí)驗(yàn)室，湖南 湘潭 411201)

計(jì)算固結(jié)系數(shù)的方法中，反彎點(diǎn)法使用方便、計(jì)算簡(jiǎn)單，但需要目測(cè)尋找反彎點(diǎn)，因而所得結(jié)果誤差比較大。本文根據(jù)太沙基一維固結(jié)理論，由固結(jié)度與時(shí)間因數(shù)推導(dǎo)計(jì)算半對(duì)數(shù)坐標(biāo)中沉降曲線斜率的表達(dá)式，通過(guò)分析土樣的沉降速率與時(shí)間得到半對(duì)數(shù)坐標(biāo)中沉降曲線的反彎點(diǎn)并計(jì)算土樣的固結(jié)系數(shù)。研究結(jié)果表明：因?yàn)榉磸濣c(diǎn)位于主固結(jié)階段，該方法可以避免初始?jí)嚎s與次固結(jié)的影響，并且只需進(jìn)行簡(jiǎn)單的計(jì)算，因此可避免圖解法中目測(cè)確定反彎點(diǎn)帶來(lái)的人為干擾。

固結(jié)系數(shù)；反彎點(diǎn)；計(jì)算

固結(jié)系數(shù)是關(guān)于土體固結(jié)速率的參數(shù)，對(duì)預(yù)測(cè)地基土沉降速率有著重要意義。目前確定固結(jié)系數(shù)使用最廣泛的方法有Taylor提出的的時(shí)間平方根法與Casagrande提出的時(shí)間對(duì)數(shù)法[1]。此外國(guó)內(nèi)外學(xué)者提出了許多不同的確定固結(jié)系數(shù)的方法，如Cour提出的反彎點(diǎn)法[2]、Sivaram提出的三點(diǎn)法[3]、Scott法[4]、Asaoka法[5]、李金軒提出的標(biāo)準(zhǔn)曲線比擬 法[6]、兩點(diǎn)法[7]、速率法[8]、剩余沉降對(duì)數(shù)法[9]和最小二乘法[10]等，這些方法由于作圖或者計(jì)算的復(fù)雜性，均沒(méi)有被廣泛使用。在Cour提出的反彎點(diǎn)法中[2]，只需要確定-lg曲線的反彎點(diǎn)，進(jìn)行簡(jiǎn)單的計(jì)算就可以得到固結(jié)系數(shù)，使用比較方便。該方法不需要固結(jié)初期與固結(jié)結(jié)束階段的數(shù)據(jù)，因此可以避免初始?jí)嚎s與次固結(jié)的影響，計(jì)算結(jié)果更能反映主固結(jié)階段的固結(jié)系數(shù)。目前使用該方法是通過(guò)圖解法來(lái)尋找反彎點(diǎn)，在-lg曲線中，通常情況下曲線的反彎點(diǎn)不是很明顯，因此會(huì)對(duì)計(jì)算結(jié)果帶來(lái)人為因素的影響。為了避免作圖法中目測(cè)反彎點(diǎn)帶來(lái)的影響，本文從太沙基固結(jié)理論出發(fā)，對(duì)與lgv之間的關(guān)系進(jìn)行分析，提出用數(shù)值計(jì)算尋找反彎點(diǎn)的方法。

1 理論基礎(chǔ)

Terzaghi一維固結(jié)方程為[11]：

式中：v為固結(jié)系數(shù)；為超靜孔隙水壓力；為深度；為時(shí)間。

平均固結(jié)度可以表示為：

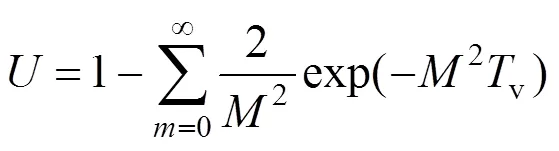
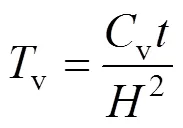
固結(jié)度與時(shí)間因數(shù)v在半對(duì)數(shù)坐標(biāo)中的曲線-lgv曲線中有一個(gè)反彎點(diǎn)[2]，在反彎點(diǎn)處曲線的斜率絕對(duì)值最大，Cour經(jīng)過(guò)推導(dǎo)，反彎點(diǎn)處v=0.405，=70%。與-lgv曲線對(duì)應(yīng)，在-lg曲線中也有一個(gè)反彎點(diǎn)，將該點(diǎn)所對(duì)應(yīng)的時(shí)間代入式(3)即可求得土體的固結(jié)系數(shù)v：

S-lgt曲線的反彎點(diǎn)需要觀察確定，在反彎點(diǎn)附近，曲線的斜率變化不大，因此反彎點(diǎn)不容易目測(cè)確定，而且受到的人為因素影響較大。本文通過(guò)數(shù)值方法分析S-lgt的反彎點(diǎn)。

2 固結(jié)系數(shù)的計(jì)算

在-lgv曲線中，曲線上點(diǎn)的斜率為[12]：

土樣的固結(jié)度可以表示為：

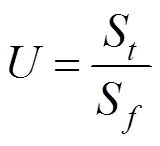
式中：表示時(shí)刻的沉降量；表示最終沉降量。

將式(3)和(6)代入式(5)可得：

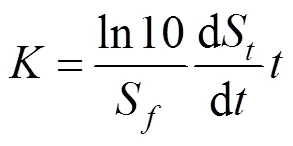
在某級(jí)荷載下，最終沉降量可認(rèn)為是常數(shù)，從式(7)可得，-lg曲線上一點(diǎn)的值與該點(diǎn)的變形速率與時(shí)間的乘積成正比，值最大的點(diǎn)即為-lg曲線上的反彎點(diǎn)。

變形曲線無(wú)法用函數(shù)表示，曲線的內(nèi)點(diǎn)用中心差商作為該點(diǎn)的沉降速率。

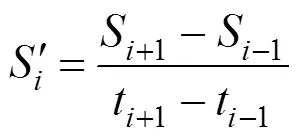
左端點(diǎn)使用向前差商作為該點(diǎn)的沉降速率。

右端點(diǎn)使用向后差商作為該點(diǎn)的沉降速率。

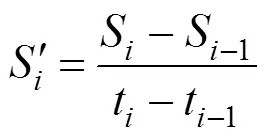
3 固結(jié)系數(shù)算例

以文獻(xiàn)[13]中的2個(gè)實(shí)例來(lái)說(shuō)明此方法的正 確性。

實(shí)例1：飽和土樣初始厚度為16.5 mm，試樣從200 kPa到400 kPa加載24 h，試樣雙面排水，試樣的沉降數(shù)據(jù)見(jiàn)表1。

將計(jì)算結(jié)果與文獻(xiàn)[9, 13?14]中提到的方法計(jì)算結(jié)果進(jìn)行對(duì)比見(jiàn)表3。

表1 算例1試驗(yàn)數(shù)據(jù)

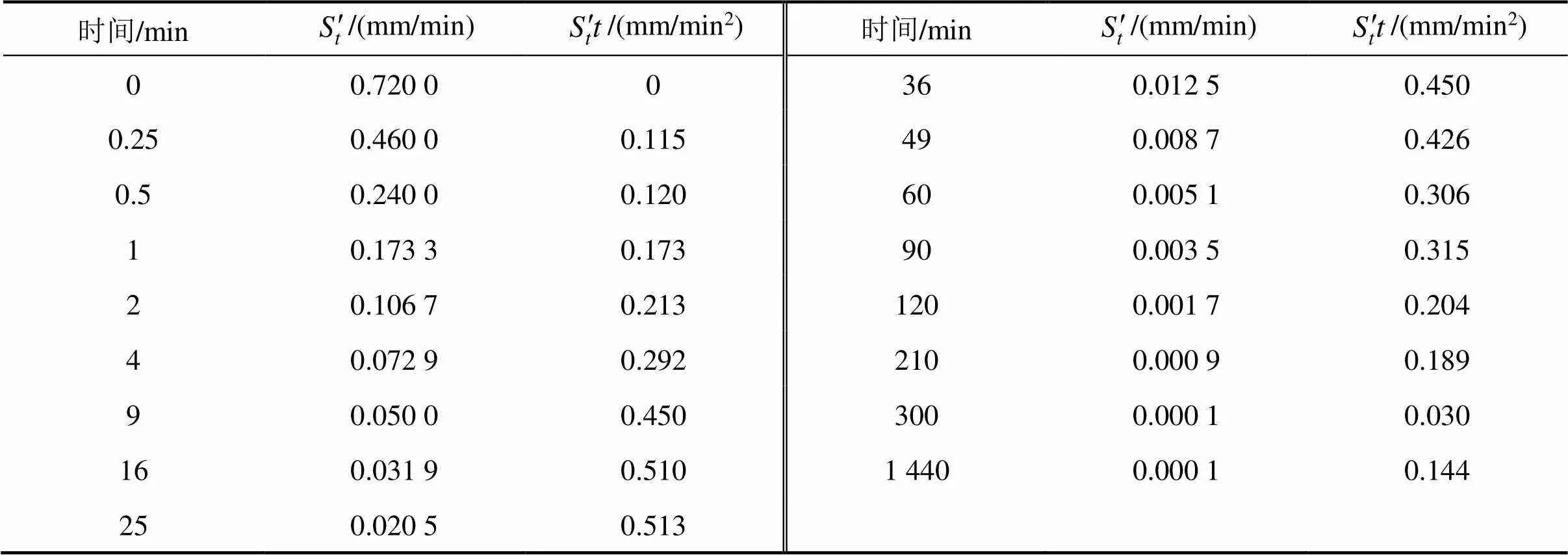
表2 算例1沉降速率數(shù)據(jù)

表3 算例1不同方法的固結(jié)系數(shù)

實(shí)例2：試樣最大排水距離為10 mm，試驗(yàn)沉降數(shù)據(jù)見(jiàn)表4。

表4 算例2試驗(yàn)數(shù)據(jù)

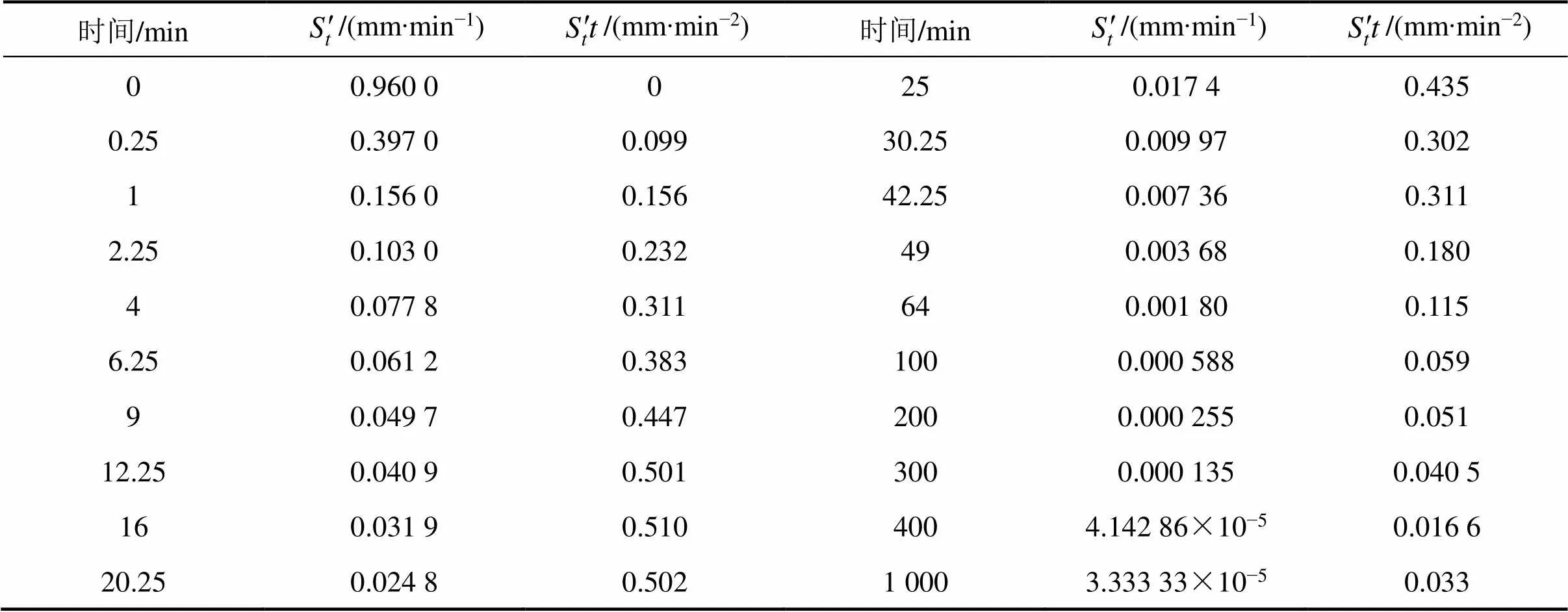
表5 算例2沉降速率數(shù)據(jù)

將計(jì)算結(jié)果與文獻(xiàn)[9, 13?14]進(jìn)行對(duì)比見(jiàn)表6。

表6 算例2不同方法的固結(jié)系數(shù)

通過(guò)以上2個(gè)算例可得，本文提出的數(shù)值反彎點(diǎn)法計(jì)算結(jié)果與時(shí)間對(duì)數(shù)法以及文獻(xiàn)[9, 13?14]中提到的計(jì)算結(jié)果相近，證明本方法是可行的。本方法中，計(jì)算參數(shù)取值在主固結(jié)階段，因此剔除了初始?jí)嚎s與次固結(jié)的影響。本方法不需作圖，也不需要目測(cè)確定反彎點(diǎn)，避免了人為因素的干擾。該方法只需進(jìn)行簡(jiǎn)單的計(jì)算，因此可以在實(shí)際工程中推廣應(yīng)用。在使用本方法時(shí)，數(shù)據(jù)點(diǎn)間隔要適當(dāng)，使差商盡可能地接近沉降曲線的斜率，反彎點(diǎn)附近對(duì)多個(gè)數(shù)據(jù)點(diǎn)進(jìn)行計(jì)算，以找到更精確的參數(shù)。

在以上幾種計(jì)算固結(jié)系數(shù)的方法中，反彎點(diǎn)法是在-lg曲線中確定=70%的時(shí)間70，時(shí)間對(duì)數(shù)法是在-lg曲線中確定=50%的時(shí)間50，張儀萍法通過(guò)推導(dǎo)出主固結(jié)沉降與沉降速率′的關(guān)系，利用-′曲線中部的直線段斜率計(jì)算固結(jié)系數(shù)。剩余沉降對(duì)數(shù)法通過(guò)主固結(jié)完成時(shí)的總沉降量∞和沉降量之差與時(shí)間在半對(duì)數(shù)坐標(biāo)系中的關(guān)系推算固結(jié)系數(shù)。沉降速率比值法通過(guò)推導(dǎo)任意相鄰兩時(shí)刻土體固結(jié)沉降速率之間的關(guān)系計(jì)算土體的固結(jié)系數(shù)。這幾種方法計(jì)算原理有差異，因此所得到的計(jì)算結(jié)果也不同影響計(jì)算固結(jié)系數(shù)的因素較多，除不同計(jì)算方法導(dǎo)致的差異性外，不同計(jì)算者使用同一種計(jì)算方法所得到的結(jié)果也不同，因此在實(shí)際工程中需要考慮選取適合的計(jì)算方法，并且保證試驗(yàn)數(shù)量。

4 結(jié)論

1) 根據(jù)太沙基一維固結(jié)理論，通過(guò)固結(jié)度與時(shí)間因數(shù)的關(guān)系推導(dǎo)了尋找沉降曲線反彎點(diǎn)的方法，從而依據(jù)反彎點(diǎn)的參數(shù)計(jì)算固結(jié)系數(shù)。

2) 本方法只需進(jìn)行簡(jiǎn)單的計(jì)算，避免了作圖法中人為因素的影響，也不需要繁瑣的計(jì)算，使用方便，處理結(jié)果與時(shí)間對(duì)數(shù)法等方法結(jié)果相近，因此本方法可以在實(shí)際工程中應(yīng)用。

3) 反彎點(diǎn)位于主固結(jié)階段，因此本方法避免了初始?jí)嚎s與次固結(jié)的影響。

[1] JTG E40—2007, 公路土工試驗(yàn)規(guī)程[S]. JTGE40—2007, Test methods of soils for highway engineering[S].

[2] Cour F R. Inflection point method for computingv[J]. J Soil Mech Fdn Engng, ASCE, 1971(1): 827?831.

[3] Sivaram B, Swamee P K. A computational method for consolidation coefficient[J]. Soils & Foundations, 1977, 17(2): 48?52.

[4] Scott R F. New method of consolidation-coefficient evaluation[J]. American Society of Civil Engineers, 1976(1): 29?39.

[5] Asaoka A. Observational procedure of settlement prediction[J]. Soils & Foundations, 1978, 18(4): 87?101.

[6] 李金軒, 胡金珠. 確定固結(jié)系數(shù)的標(biāo)準(zhǔn)曲線比擬法[J]. 工程勘察, 1996, 23(1): 21?22. LI Jinxuan, HU Jinzhu. The specification curve analogue method for calculating coefficient of consolidation[J]. Geotechnical Investigation & Surveying,1996, 23(1): 21? 22.

[7] Prasad Y V S N, Rao S N. A new two point method of obtainingvfrom a consolidation test[J]. Canada Geotechnical Journal, 1995, 32: 741?746.

[8] Parkin A K. Coeffcient of consolidation by the velocity method[J]. Géotechnique, 1978, 28(4): 472?474.

[9] 李濤, 張儀萍, 曹國(guó)強(qiáng), 等. 推算室內(nèi)固結(jié)系數(shù)的剩余沉降對(duì)數(shù)法[J]. 巖土工程學(xué)報(bào), 2003, 25(6): 724?726. LI Tao, ZHANG Yiping, CAO Guoqiang, et al. Study on evaluation of consolidation coefficient[J]. Chinese Journal of Geotechnical Engineering, 2003, 25(6): 724－726.

[10] 包太, 劉新榮, 朱凡, 等. 固結(jié)系數(shù)的最小二乘法計(jì)算[J]. 巖土工程學(xué)報(bào), 2005(10): 1230?1232. BAO Tai, LIU Xinrong, ZHU Fan, et al. Least square method for the consolidation coefficient evaluation[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(10): 1230?1232.

[11] 李廣信. 高等土力學(xué)[M]. 1版. 北京: 清華大學(xué)出版社, 2004. LI Guangxin. Advanced soil mechanics[M]. 1st ed. Beijing: Tsinghua University Press, 2004.

[12] Parkin A K, Mesri G, FENG T W. Coefficient of consolidation by inflection point method[J]. Journal of Geotechnical & Geoenvironmental Engineering, 2000, 126(12): 716?718.

[13] 張儀萍, 俞亞南, 張土喬, 等. 室內(nèi)固結(jié)系數(shù)的一種推算方法[J]. 巖土工程學(xué)報(bào), 2002, 24(5): 616?618. ZHANG Yiping, YU Yanan, ZHANG Tuqiao, et al. A method for evaluating coefficient of consolidation[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(5): 616?618.

[14] 王軍保, 劉新榮, 李鵬. 用沉降速率比值法計(jì)算固結(jié)系數(shù)的探討[J]. 巖土力學(xué), 2011, 32(10): 3085?3088. WANG Junbao, LIU Xinrong, LI Peng. Discussion on the calculation of consolidation coefficient by sedimentation rate ratio[J]. Rock and Soil Mechanics, 2011, 32(10): 3085? 3088.

Numerical method for consolidation factor on reserve bend point

LIN Liping1, LIU Keding1, HE Jianqing2, YAO Qi2

(1. Hunan Urban Construction College, Xiantan 411101, China; 2. Hunan Provincial Key Laboratory of Geotechnical Engineering for Stability Control and Health Monitoring, Hunan University of Science and Technology, Xiantan 411201, China)

Among the different methods of calculating the coefficient of consolidation, the inflection point method is easier to use. But it can cause larger error range because the point of inflection is visually determined. According to Terzaghi’s one-dimensional consolidation theory, the relationship between the logarithm of time factor and consolidation degree was obtained to calculate inflection point in the curve. Analysis of the settlement rate and time of soil samples to get the inflection point and the consolidation coefficient of soil sample was calculated. Because of the inflection point is in the primary consolidation stage, this method can avoid the influence of initial compression and secondary consolidation. This method only needs simple calculation, so it can avoid the human interference for the inflection point that visual determined.

consolidation coefficient; inflection point; calculation

TU433

A

1672 ? 7029(2020)03 ? 0623 ? 05

10.19713/j.cnki.43?1423/u.T20190652

2019?07?18

湖南省自然科學(xué)基金資助項(xiàng)目(2019jj40056)；湖南省教育廳科學(xué)研究重點(diǎn)項(xiàng)目(18A345)

劉可定(1973?)，女，湖南湘潭人，副教授，從事結(jié)構(gòu)方向的教學(xué)和科研工作；E?mail：307238731@qq.com

(編輯 涂鵬)