考慮變應力幅非線性累計損傷的高速鐵路鋼桁拱橋疲勞分析

張旭，藺鵬臻

考慮變應力幅非線性累計損傷的高速鐵路鋼桁拱橋疲勞分析

張旭，藺鵬臻

(蘭州交通大學 土木工程學院，甘肅 蘭州 730070)

為分析鋼結構橋梁在變應力幅循環條件下的疲勞壽命，基于非線性累計損傷方程，建立考慮變應力幅的疲勞損傷指標計算公式。以某高速鐵路鋼桁架拱橋為例，對比分析線性方法、等效應力幅法、遞推法以及本文方法求解得到的疲勞壽命。研究結果表明：線性模型的計算結果偏小，等效應力幅法的計算誤差隨應力幅差值的增大而增大，遞推法的計算精度高但運算量太大，本文提出的方法不僅能客觀地反應疲勞損傷的過程，計算量小，而且計算結果與遞推法的計算結果基本相同。對于鋼桁架拱橋，豎腹桿的疲勞壽命最低，且同一根桿件的不同位置疲勞損傷相差往往很大，以豎腹桿為例，該類桿的下端、靠鐵軌處的疲勞壽命最低，容易出現疲勞問題，在構造設計、施工質量方面應更加予以關注。

非線性損傷；疲勞壽命；變應力幅；鋼桁拱橋

橋梁在長時間的連續反復荷載作用下，容易出現即使應力很低，構件也會突然發生脆性斷裂這類疲勞破壞的現象[1]。由于實際橋梁中動載引起的應力循環大多數為變應力幅循環，為了預測疲勞壽命，人們提出了多種線性與非線性理論。目前工程中大都采用Miner線性理論分析結構的疲勞損傷，但該理論認為損傷與載荷的作用次序無關，所以不能客觀地反映疲勞損傷的過程[2]。由此，國內外學者針對非線性損傷進行了大量研究：Lemaitre[3]基于連續介質熱力學和耗散能理論，建立了非線性的高周疲勞損傷公式，WANG等[4?5]對公式中的系數做了系統的分析，并結合懸索橋梁加以運用，ZHAN等[6]通過考慮平均應力的影響，提出了從疲勞實驗數據中獲取材料參數的方法，LI等[7?8]提出了橋梁結構疲勞非線性累計損傷模型，蔡曉靜等[9]通過實驗找到平均應力對S-N曲線的影響關系，賈單鋒等[10]通過高周疲勞實驗找到Q345級鋼的S-N曲線。目前，在利用Lemaitre方程求解非線性疲勞損傷時，無論用等效應力幅代替各個應力幅[5]，或用繁瑣的遞推公式[11]，均不能在變應力幅循環條件下準確方便地計算出疲勞損傷。本文在前人研究的基礎上，通過分析應力循環塊中每個應力幅對總疲勞壽命的影響，建立變應力幅循環條件下的疲勞損傷指標計算公式。結合實際算例發現：本文提出的方法計算精度高、計算量小，鋼桁拱橋這類橋梁，豎腹桿的疲勞壽命最小、上弦桿最大，工程中應重點關注豎腹桿的構造設計與施工質量。

1 非線性累計疲勞損傷指標

1.1 疲勞損傷指標的定義

損傷力學中，以損傷指標來反映材料的劣化過程[12]。當損傷指標達到1時，結構發生破壞：

式中：為名義橫截面積；為考慮損傷后的有效截面面積。

為便于理解，對單軸應力循環塊中涉及的符號進行說明，見圖1。

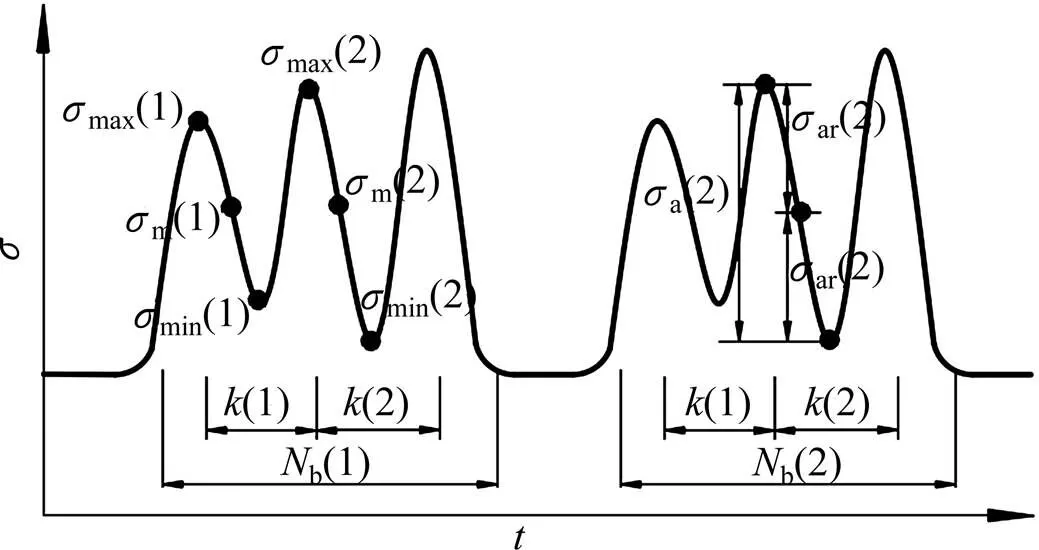
圖1 單軸應力循環塊中各符號示意圖

圖1中：m為平均應力；max和min分別為最大、最小應力；a為應力幅；ar為半應力幅；b為應力循環塊的個數；為當前應力循環塊中應力幅的數量。

1.2 高周疲勞演化方程

在單軸應力狀態下，Lemaitre建立的高周疲勞演化方程[3]可簡化為：

為便于分析，假定平均應力m等于0，且由于一個應力循環塊中應力幅的數量較少，可認為疲勞損傷指標在一個應力循環塊中沒有變化。在一個應力循環塊中對式(2)積分可得

式(3)求解：

為考慮平均應力的影響，根據SWT方程[13]

將式(5)回代到式(4)：

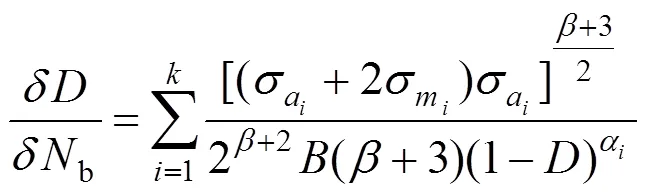
1.3 等效應力幅法

根據損傷等效原則[5]，得到等效應力幅

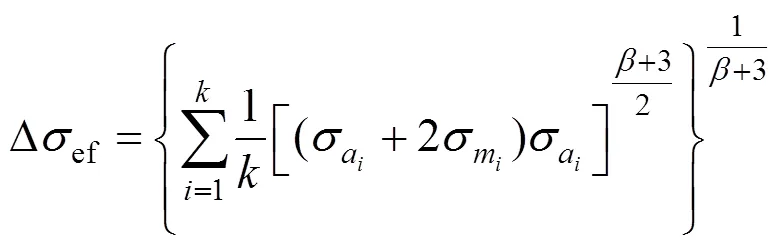
對式(6)進行積分，將式(7)代入，并取與等效應力幅Δef對應的系數e，得到考慮平均應力的疲勞損傷指標計算公式

1.4 遞推法

對式(4)等號右邊的單個應力幅進行積分[11]，并結合式(5)，得到考慮平均應力時，全壽命周期中第個應力幅作用前后的疲勞損傷指標關系。

2 考慮變應力幅的疲勞損傷指標

2.1 各應力幅造成的疲勞損傷指標之間的比例關系

將式(11)代入式(4)：

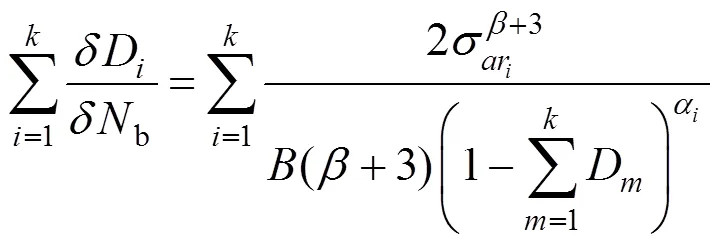
令等號兩邊各個表達式分別相等：

2.2 總疲勞損傷指標

利用式(10)，將式(13)等號右邊的疲勞壽命用表示：

為了表示方便，將式中的求和公式記為：

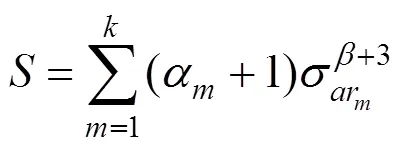
對式(14)積分：

對求和，得到總疲勞損傷指標：

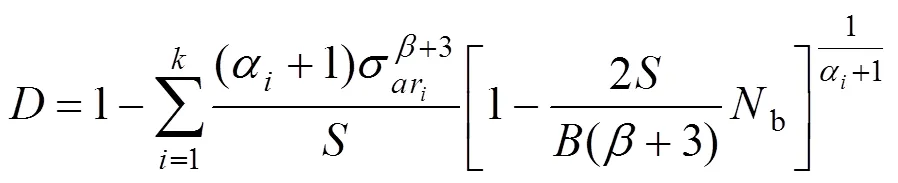
為了考慮平均應力的影響，且表示方便，記：

得到考慮平均應力的疲勞損傷指標：

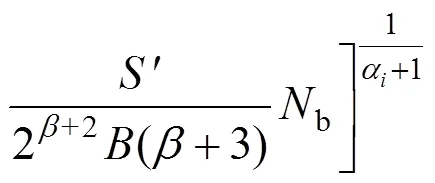
系數由公式=113?0.17×a確定[14]。分析英國鋼結構疲勞設計規范[15]中螺栓連接(E連接類型)對應的S-N曲線[16]，得出系數=0，=4.868×1013。

3 系數α對非線性模型的影響

3.1 對比樣本的設置

設置3個應力循環塊作為對比分析樣本。每個樣本中設置2個應力幅，應力幅的差值分別設為40，70和100 MPa，且不考慮平均應力的影響，即m=0。各樣本的應力幅a和等效應力幅Δef，見表1。

表1 對比分析樣本

3.2 誤差分析

因為遞推法通過疊加每個應力幅造成的損傷進行計算，不存在系數取值不準確的問題，所以以遞推法的計算結果為參照，分析其余2種非線性模型的誤差。利用MATLAB軟件，根據式(8)，(9)和(19)，計算得到3種非線性模型的疲勞損傷指標與應力循環次數的函數關系曲線見圖2，誤差率以及用時見表2。

表2 不同計算方法的誤差率與用時

圖2 累計疲勞損傷曲線

進一步分析應力循環塊中應力幅的差值程度對等效應力幅法計算精度的影響，令應力循環塊中含有2個應力幅，范圍分別在0~500 MPa。在忽略平均應力的條件下，計算出疲勞壽命的誤差率，見圖3。

圖3 等效應力幅法的誤差率

分析結果表明：非線性計算模型可以客觀地反應疲勞破壞的突發性，本文提出的方法的計算結果與遞推法的計算結果近乎相同，誤差率不超過1.0%，且計算量遠小于遞推法。等效應力幅法的計算誤差隨著應力幅差值的增大而增大，在應力幅為100 MPa的范圍內，應力幅的差值引起的誤差可達3.0%左右。

4 高速鐵路鋼桁拱橋疲勞分析

4.1 橋梁概況

以某3×168 m鐵路連續鋼桁架拱橋為例，如圖4所示，分析該橋的疲勞壽命。該橋的主梁采用下承式鋼桁梁結構，主桁采用有豎桿的三角形桁式，桁寬13.8 m和高12.8 m，上、下弦節間長度分別為11 m和12 m，采用正交異性鋼橋面板和混凝土道碴槽板的橋面體系，吊桿為八角形截面，拱肋線形為二次拋物線，矢高28 m，矢跨比1/4.71，全橋材質為Q345qE鋼材，支座均為球形鋼支座。

單位：m

4.2 有限元模型

采用ANSYS15.0軟件進行有限元建模。對于桁架橋，桿系結構能反應橋梁整體的力學行為，因此除橋面板采用板單元shell181模擬外，其余桿件均用3D梁單元beam189模擬，梁單元之間固結連接。全橋的有限元模型共計梁單元5 189個，板單元2 106個，見圖5。圖4中79 m處A、B節點的有限元模型以及截面的4個角點的位置編號見圖6，單元局部坐標系為：軸為桿單元軸向方向，與軸為截面高寬方向。主要桿件的截面特性值見表3，括號里為支座附近桿件的特性值。

圖5 有限元模型(半跨)

圖6 橋梁A，B節點處的有限元模型

表3 各類桿件的截面幾何特性

4.3 疲勞荷載

整體動力分析中的荷載主要包括：自重、二期恒載、列車荷載。鋼材容重為76.98 kN/m3，二期恒載取175 kN/m。列車荷載采用高速鐵路典型疲勞列車，編組模式為2節機車+8節客車[17]，雙線同時加載，對向行駛，設計時速為250 km/h，軸重1取為140 kN，軸重2取為230 kN，軸重布置見圖7。

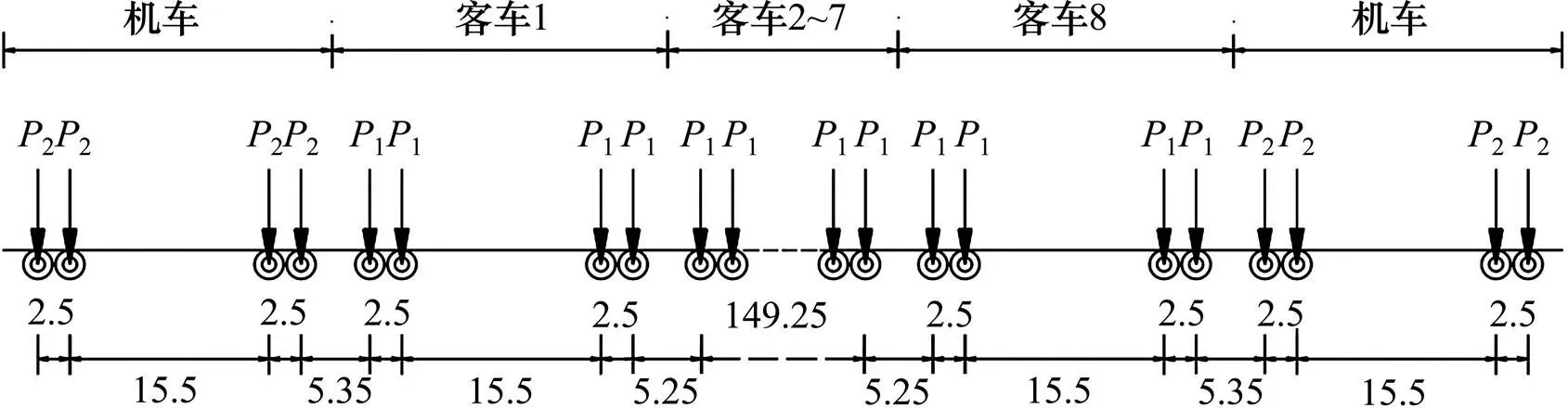
單位：m

列車荷載在模型上的實現采用當載荷移動過程中落在移動方向2相鄰節點之間時，載荷按線性插值分配給前、后節點的方法[18]。

4.4 典型桿件疲勞應力分析

材料阻尼為0.005，運動方程采用直接積分法求解，計算得到各桿件的截面邊緣處的軸向應力時程曲線后，發現該橋的豎腹桿、斜腹桿、下弦桿、吊桿及上弦桿為受拉桿件，易發生疲勞破壞[19]。

雙線加載的條件下，當列車行駛1.402 s至97.4 m時，位于78 m(426 m)處的B節點下弦桿的拉應力為各桿件在加載全過程中的最大值，此時刻各桿件的軸向應力云圖見圖8，需重點分析B節點附近各桿件的應力幅情況。

經過計算得知，全部受拉桿件中節點B的豎腹桿的角點2處的軸向應力幅最大，其應力時程曲線見圖9，經過雨流計數法[20]統計后得到的雨流矩陣圖見圖10。A，B節點各桿件的截面的各角點的軸向最大應力幅見表4，各桿件的最大應力幅見圖11(左)。

單位：Pa

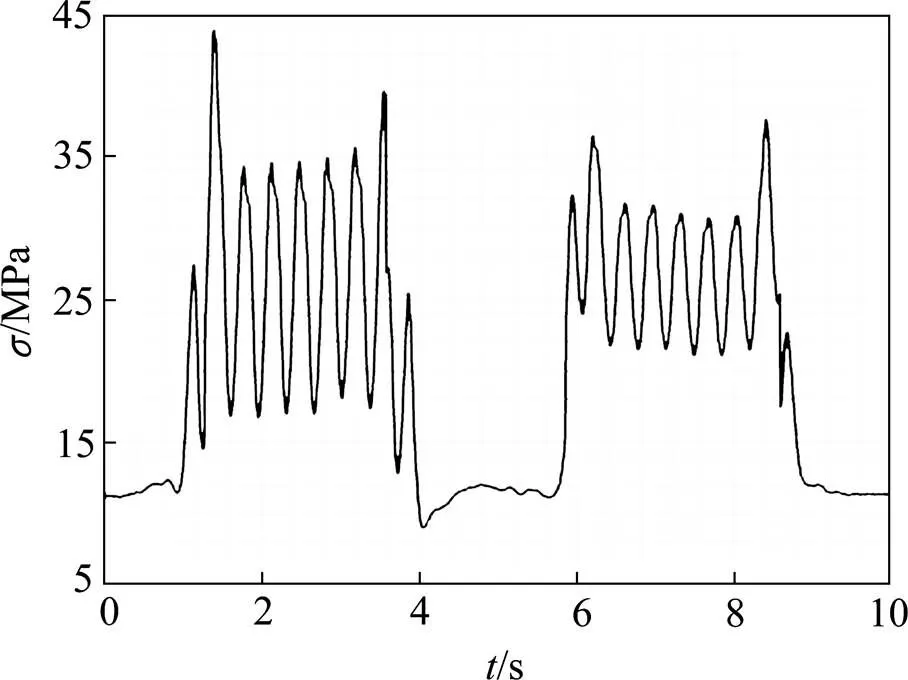
圖9 節點B豎腹桿的角點2的軸向應力時程曲線

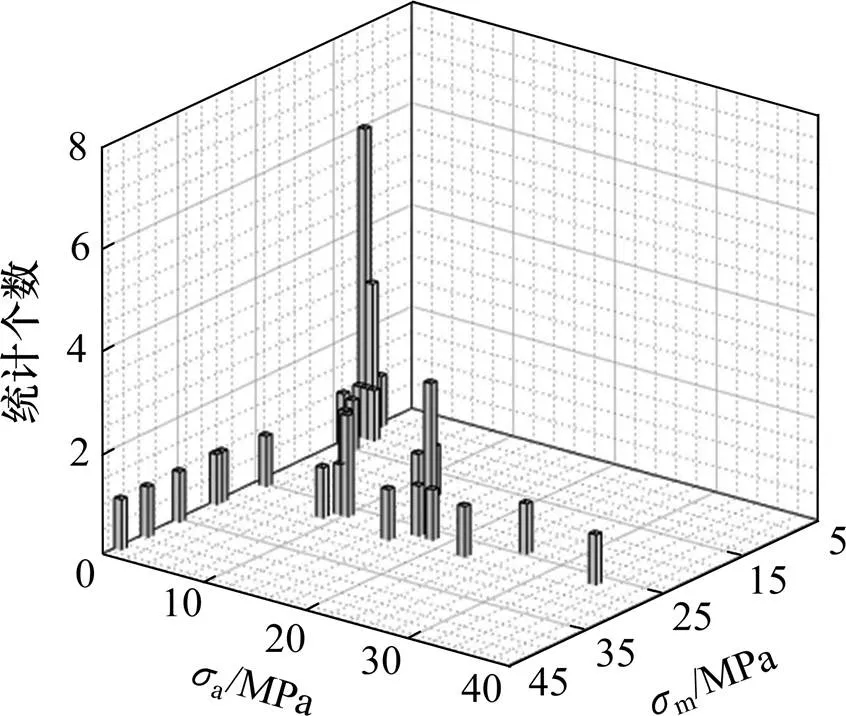
圖10 節點B豎腹桿角點2的雨流矩陣圖

應力分析結果表明：拉應力最大的桿件不一定應力幅最大，但應力幅最大的桿件會在其附近出現。同一根桿件的不同位置受動載影響的程度不同：豎腹桿、斜腹桿和吊桿下端的應力幅大于上端，上弦桿和下弦桿節點處大于節間處，豎腹桿、斜腹桿靠近鐵路線的內側大于外側，下弦桿、上弦桿上邊緣大于下邊緣，吊桿遠離鐵路線的外側大于 內側。

表4 節點A，B處各桿件的最大軸向應力幅

4.5 分析疲勞壽命

分別用線性計算法[19]、等效應力幅法、遞推法和本文方法計算各桿件的疲勞壽命。節點A，B處各桿件應力幅最大的角點處的疲勞壽命見表5。用遞推法算得所有受拉桿件中應力幅最大的角點處的疲勞壽命見圖11(右)。

表5 節點B豎腹桿的疲勞壽命

本橋設計使用壽命100 a，參考運量大于3 000萬噸/a的最不利情況，每天過橋的客車取270節，過橋的車次約為34次[17]，計算得到設計疲勞壽命為1.22×106次，而全橋的疲勞壽命由節點B處的豎腹桿決定，該處的計算疲勞壽命為9.238×106次，大于設計值，滿足設計要求。

疲勞損傷計算結果表明：當應力幅的平均應力較大時，線性模型計算出的疲勞壽命偏大，當應力循環塊中含多個大于應力疲勞極限的應力幅時，等效應力幅法的誤差較大，本文方法的計算結果與遞推法的計算結果幾乎完全相同。應力幅和平均應力與疲勞壽命的關系為負相關，兩者共同決定疲勞壽命，受拉桿件的疲勞壽命的大致規律由低到高為：豎腹桿＜斜腹桿＜下弦桿＜吊桿＜上弦桿。

圖11 橋梁各桿件的最大應力幅(左)和疲勞壽命(右)

5 結論

2) 算例分析表明，本文推導的非線性累計損傷公式的計算結果與遞推法的計算結果幾乎完全相同，計算量與等效應力幅法的計算量基本相同，在實際工程中更加易于應用，而且與線性方法相比，本文方法能更客觀地反應疲勞損傷過程。

3) 對于多跨鋼桁架拱橋，跨中處受拉桿件的疲勞壽命由低到高為：豎腹桿<斜腹桿<下弦桿<吊桿<上弦桿，因此在工程設計中應適當增大豎腹桿的橫截面積、優化連接方式，施工中注意提高施工質量，使這類桿件受動載引起的應力幅盡可能減小。

4) 疲勞壽命不僅與桿件類型有關，還與桿件的細部位置有關，以豎腹桿為例，該類桿的底端、靠軌道處的疲勞壽命最低，更易出現疲勞問題。

[1] 趙少杰, 任偉新. 超限超載交通對橋梁疲勞損傷及可靠度的影響[J]. 中南大學學報(自然科學版), 2017, 48(11): 3044?3050. ZHAO Shaojie, REN Weixin. Effect of overrun and overloaded vehicles on fatigue damage and reliability of highway bridges[J].Journal of Central South University (Science and Technology), 2017, 48(11): 3044?3050.

[2] 項海帆. 高等橋梁結構理論[M].2版. 北京: 人民交通出版社, 2013. XIANG Haifan. Advanced theory of bridge structures [M]. 2nd ed. Beijing: China Communications Press, 2013.

[3] Lemaitre J. A course on damage mechanics[M]. 2nd ed. Berlin: Springer-Verlag Berlin Heidelberg, 1996.

[4] WANG Huili, QIN Sifeng, WANG Yunjie. Nonlinear cumulative damage model and application to bridge fatigue life evaluation[J]. Advances in Structural Engineering, 2018, 21(9): 1402?1408.

[5] 王會利, 秦泗鳳, 譚巖斌. 考慮非線性累計損傷的橋梁疲勞壽命分析[J]. 大連理工大學學報, 2016, 56(4): 362?366. WANG Huili, QIN Sifeng, TAN Yanbin. Fatigue life analysis of bridges considering nonlinear cumulative damage[J]. Journal of Dalian University of Technology, 2016, 56(4): 362?366.

[6] ZHAN Zhixin, HU Weiping, ZHANG Miaomeng. Revised damage evolution equation for high cycle fatigue life prediction of aluminum alloy LC4 under uniaxial loading[J]. Applied Mathematics & Mechanics, 2015, 36(9): 1185?1196.

[7] LI Z X, CHAN T H T, KO J M. Fatigue analysis and life prediction of bridges with structural health monitoring data — Part I: methodology and strategy[J]. International Journal of Fatigue, 2001, 23(1): 45?53.

[8] CHAN T H T, LI Z X, KO J M. Fatigue analysis and life prediction of bridges with structural health monitoring data—Part II: application[J]. International Journal of Fatigue, 2001, 23(1): 55?64.

[9] 蔡曉靜, 許金泉. 各種平均應力下高周疲勞極限間的定量關系[J]. 工程力學, 2015, 32(10): 25?30. CAI Xiaojing, XU Jinquan. A quantitative relationship of high cycle fatigue limit with mean stresses[J]. Engineering Mechanics, 2015, 32(10): 25?30.

[10] 賈單鋒, 廖小偉, 崔佳. Q345qD橋梁鋼高周疲勞性能及-P-S-N曲線試驗研究[J]. 天津大學學報, 2016, 49(4): 122?128. JIA Danfeng, LIAO Xiaowei, CUI Jia. Experimental study on high cycle fatigue behavior and-P-S-N curves of bridge steel Q345qD[J]. Journal of Tianjin University (Science and Technology), 2016, 49(4): 122?128.

[11] 陳志為, 徐幼麟. 考慮非線性累計損傷的大跨多荷載橋梁的疲勞可靠度評估[J]. 西南交通大學學報, 2014, 49(2): 213?219. CHEN Zhiwei, XU Youlin. Fatigue reliability analysis of multi-loading suspension bridges considering nonlinear accumulative damage[J]. Journal of Southwest Jiaotong University, 2014, 49(2): 213?219.

[12] 張彥軍, 張淼. 基于損傷力學方法的帶板連接件疲勞壽命預估[J]. 機械強度, 2011, 33(3): 443?449. ZHANG Yanjun, ZHANG Miao. Fatigue life prediction of the joint plate based on damage mechanics method[J]. Journal of Mechanical Strength, 2011, 33(3): 443?449.

[13] Dowling N E. Mean stress effects in strain-life fatigue[J]. Fatigue & Fracture of Engineering Materials & Structures, 2009, 32(12): 1004?1019.

[14] LI Z X, CHAN T H T, KO J M. Fatigue damage model for bridges with under traffic loading: application made to Tsing Ma Bridge[J]. Theoretical and Applied Fracture Mechanics, 2001, 35(1):81?91.

[15] BS 7608—1993, Fatigue design and assessment of steel structures British standard[S].

[16] CHEN Z W, XU Y L, XIA Y. Fatigue analysis of long-span suspension bridges under multiple loading case study[J]. Engineering Structures, 2011, 33(12): 3246? 3256.

[17] 楊鑫炎. 高速鐵路鋼橋疲勞評估標準車型研究[J]. 城市道橋與防洪, 2014, 28(7): 331?333. YANG Xinyan. Research on fatigue evaluation standard model of high speed railway steel bridge[J]. Urban Roads Bridges & Flood Control, 2014, 28(7): 331?333.

[18] 朱世峰, 馬明, 周志祥. 計算結構動力響應中移動載荷的簡化方法[J]. 四川建筑, 2008, 28(2): 139?141. ZHU Shifeng, MA Ming, ZHOU Zhixiang. A simplified method for calculating the moving load in structural dynamic response[J]. Sichuan Architecture, 2008, 28(2): 139?141.

[19] GB 50017—2017, 鋼結構設計標準[S]. GB 50017—2017, Standard for design of steel structures [S].

[20] 畢繼紅, 陳花麗, 任洪鵬. 基于雨流計數法的接觸線疲勞壽命分析[J]. 鐵道學報, 2012, 34(6): 34?39. BI Jihong, CHEN Huali, REN Hongpeng. Analysis on fatigue life of contact wire based on rain-flow counting method[J]. Journal of the China Railway Society, 2012, 34(6): 34?39.

Fatigue analysis of high-speed railway steel trussed arch bridge considering nonlinear cumulative damage of variable stress range

ZHANG Xu, LIN Pengzhen

(School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

In order to analyze the fatigue life of steel bridge under variable stress range cycle, based on the nonlinear cumulative damage equation, the fatigue damage index considering variable stress range was established. Taking a high-speed railway simply supported steel truss bridge as an example, the effects of Linear Method, Equivalent Stress Range Method, Recursive Method and the method of this paper on fatigue life calculation results were compared and analyzed. The results show that the calculation result of the Linear Model smaller than other method, and the error of the calculation results of the Equivalent Stress Range Method increases with the increase of the stress range difference. The accuracy of the Recursive Method is high but the calculation amount is too large. The method proposed in this paper can objectively reflect the process of fatigue damage, and its calculation results are basically the same as those of the Recursive Method. For steel trussed arch bridges, the fatigue damage at different positions of the same rod is often very different. Taking the vertical web as an example, the fatigue life is the lowest near the rail and the bottom of the rod, which is relatively prone to fatigue problems. More attention should be paid to the structural design and construction quality of such rods.

nonlinear damage; fatigue life; variable stress range; steel trussed arch bridges

U24

A

1672 ? 7029(2020)03 ? 0540 ? 09

10.19713/j.cnki.43?1423/u.T20190561

2019?06?23

國家自然科學基金重大項目(11790281)；國家自然科學基金資助項目(51878323)；中國鐵路總公司科技研究開發計劃課題(2017G010-C)

藺鵬臻(1977?)，男，甘肅甘谷人，教授，博士，從事橋梁結構設計理論的研究；E?mail：pzhlin@mail.lzjtu.cn

(編輯 涂鵬)