最大相關熵準則下多層極端學習機的批量編碼

劉兆倫，武 尤，王衛濤，張春蘭，吳 超，劉 彬，

1(燕山大學 河北省特種光纖與光纖傳感重點實驗室，河北 秦皇島 066004)2(燕山大學 信息科學與工程學院，河北 秦皇島 066004)3(燕山大學 電氣工程學院，河北 秦皇島 066004)

1 引 言

近年來，為了克服基本極端學習機(extreme learning machine，ELM)及其改進算法提取特征能力差[1]，難以有效處理圖像、視頻等自然信號的問題[2]，基于稀疏編碼的多層極端學習機(HELM)作為一種多層神經網絡被提出[3]，其與傳統的疊加式自動編碼器(SAE)相比，訓練時間可以從小時縮短到秒[4]，在圖像處理[5-8]和非線性模型辨識[9，10]等領域得到了廣泛的研究.但在其應用過程中，HELM暴露出一些明顯且公認的缺點，即其在進行大樣本數據集學習時所產生的巨大運行內存需求，以及當訓練集中存在噪聲等異常數據時，HELM的學習效果變差且過擬合現象明顯.

HELM在運行過程中內存占用較大的主要原因是：為保證HELM的學習精度，其決策層中的隱含層神經元數量往往需要被設置得很大，這使得參與計算的特征矩陣維度升高，從而導致運行內存需求的劇增.目前學者們針對HELM內存需求大的問題也多從降低決策層特征矩陣維度這個角度出發，通過PCA等多種算法實現對HELM的決策層隱含神經元數量的縮減來提出改進，如Wong Chi-man等將核學習引入HELM中來減小運行內存[11]；Zhou Hong-ming等人利用主成分分析法逐層對隱含層輸出的特征矩陣進行降維以降低內存占用[12]；Henríquez等人提出一種基于Garson算法的非迭代方法對隱含層神經元進行剪枝實現降低運行內存的目的[13].盡管這些方法均實現了減少運行內存的目的，但是增加的算法無疑會導致計算復雜度的上升和模型結構復雜度的增加，從而使運算時間變長、學習速度變慢.針對這一問題，Liang Nan-ying等人提出的一種在線極端學習機[14]，可以實時根據新到來的數據對輸出層權重矩陣進行矯正更新，給極端學習機處理大樣本數據提供了一種將訓練數據分批次進行學習的方法，也為降低多層極端學習的模型復雜度提供了思路.

HELM在訓練集中存在噪聲等異常數據時，學習效果變差且易發生過擬合現象的原因是：HELM中的最小均方差準則(MMSE)默認數據誤差呈高斯分布[15]，這在實際應用數據中這樣的假設明顯是不合理的.針對這個問題Xing Hong-jie等人提出了基于相關熵準則(MMC)的極端學習機[16]，提升了極端學習機應對異常數據的性能，降低模型對異常點的敏感性從而改善模型的過擬合問題.如Chen Liang-jun等人，用MCC準則代替傳統多層極端學習機(multilayer extreme learning machines，ML-ELM)決策層中的MMSE準則，使ML-ELM的魯棒性和過擬合現象得到改善[3].唐哲等人將MCC準則應用于半監督學習算法中，有效地提高了半監督學習算法的學習性能[17].Luo Xiong等人將一種堆疊式多層極端學習機(stacked extreme learning machine，S-ELM)中的MMSE準則替換為MCC準則，實現了S-ELM學習精度的進一步提高[18].這都為本文將MCC準則引入HELM決策層提供了理論基礎和方法指導.

根據上述多層極端學習機現存的問題和在線極端學習機、相關熵準則等方法的啟發，本文提出一種基于最大相關熵準則的批量編碼式多層極端學習機.在原始多層極端學習機的決策層中引入最大相關熵準則，構建基于最大相關熵準則的多層極端學習機.基于最大相關熵準則的多層極端學習機(MCC-HELM)分批次對由大數據集分解得到的多個小數據集進行學習，接著利用在線極端學習機的方法，將多個批次的學習數據，在MCC-HELM的決策層實現融合，構成基于最大相關熵準則的批量編碼式多層極端學習機(BC-HELM)，并得到最終的學習結果.最后通過仿真實驗確定其網絡參數并通過與其他多層極端學習機對比來驗證其性能.

2 基于最大相關熵準則的批量編碼式多層極端學習機

2.1 多層極端學習機與最大相關熵準則的結合

原始多層極端學習機由兩部分組成：基于稀疏自動編碼器的無監督特征學習和基于傳統極端學習機的有監督決策[19].而決策層中傳統極端學習機是基于MMSE準則來建立目標函數的，由于該準則對異常點極為敏感，傳統極端學習機在應用過程中極易出現過擬合現象.于是本文將原始多層極端學習機決策層中的MMSE準則使用MCC準則代替，設輸入的訓練樣本數為S，隱含層神經元個數為L到，得到新的目標函數：

(1)

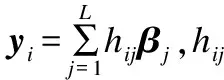
(2)

式(2)中σ為尺度因子，τ為正則化參數。針對上述非線性優化問題，采用半二次優化技術通過迭代方法進行求解，目標函數為：

(3)

對式(3)進行求導得到：

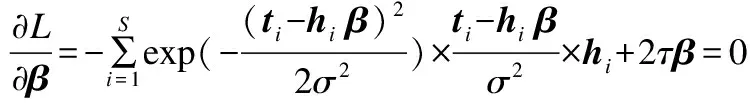
(4)

根據半二次優化技術中的共軛凸函數理論[20]，式(4)中的高斯核的部分暫時使用對角矩陣中Λ表示即：

(5)

于是式(4)整理為矩陣形式變為：

(6)

由于多層極端學習機是針對大樣本數據集的處理提出的，因此本文默認訓練樣本數遠遠大于隱含層神經元的數目，則對式(6)進行求解得到輸出權值矩陣的表達式為：

β=[2τσ2I+HTΛH]-1HTΛT

(7)

于是得到迭代表達式：

(8)

式(8)中的對角矩陣Λ是根據半二次優化技術中的共軛凸函數理論建立的，來表示目標函數中高斯核的部分.其中對角矩陣Λt+1中的Λii對應第i組數據通過上一次迭代得到的輸出權重βt而求得的學習輸出與目標輸出之間的距離；βt+1表示根據Λt+1中的距離更新得到的新的輸出權重矩陣.設輸出數據維度為m，設置一個轉換矩陣φ∈(S×m)，令：

β=HTφ

(9)

同時將式(7)中等號右邊求逆的部分換回等號左邊，則式(7)重構為：

[2τσ2I+HTΛH]HTφ=HTΛT

(10)

將式(10)等號右邊中的HT乘進括號中，等號兩邊便能夠同時抵消掉最右邊的HT，于是式(10)寫為：

[2τσ2I+ΛHHT]φ=ΛT

(11)

由核函數理論可知，存在低維輸入空間中的核函數k(x,x′)與高維特征空間中的內積〈φ(x)·φ(x′)〉相等[21]，即核函數用來代替式(11)表達式中的內積計算，則：

[2τσ2I+ΛK]φ=ΛT

(12)

同理，將式(9)的變換代入式(5)中，并將對角矩陣Λ中的內積計算由核函數形式代替，得到：

(13)

式(13)中Ki表示第i個數據對應隱含層輸出的特征矩陣的內積hihiT，式(12)中K表示由Ki組成的對角矩陣，這里由于只需計算對角線上的數值，因此即使核變換導致運算矩陣的維度由L×L升高至S×S但是計算量卻大大下降，避免了計算量因隱含神經元數目的增加而劇增的問題，于是經過式(9)變換后得到MCC-HELM的決策層即MCC-ELM的迭代公式為：

(14)

MCC-HELM結構如圖1所示.

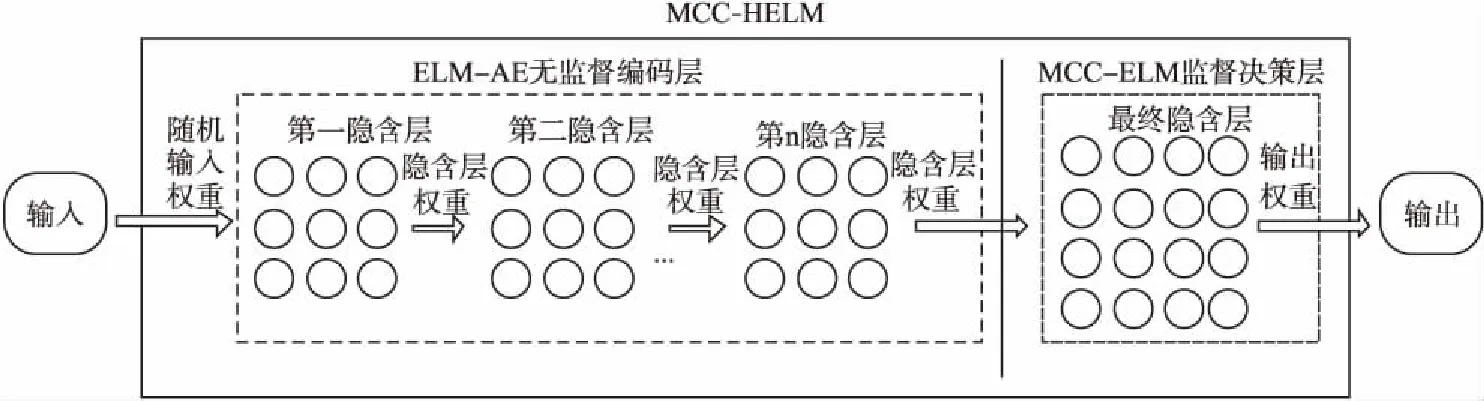
圖1 MCC-HELM結構Fig.1 MCC-HELM network

2.2 最大相關熵準則下多層極端學習機批量編碼的實現

在保證學習效果的前提下，訓練數據的個數越多則需要的隱含層神經元數量越大.于是本文將訓練數據平均分為D組，每組數據形成一個批次，分別通過MCC-HELM進行學習，從而降低每一個MCC-HELM對最后決策層中隱含層神經元數量的需求.最后將在線極端學習機的方法引入進來，將當前組的MCC-HELM的決策層與歷史組數據的MCC-HELM決策層結合再完成決策.這樣一來，每一次的決策都是在綜合歷史訓練數據通過多層稀疏自動編碼器學習到的所有特征信息的基礎上進行的，因此保證了學習結果的可靠性，達到保證精度的同時縮小內存需求的要求.

由于在融合決策階段涉及到整體求逆的問題，為了減小求逆的時間，不再進行式(9)以及核矩陣的轉換，仍然轉換為原始極端學習機中當訓練數據遠遠大于隱含層神經元時的輸出權重表達式的形式，從而減小融合決策時需要進行求逆的矩陣的維度，縮短計算時間。用A表示由各批次數據的迭代結果Λ所組成的融合對角矩陣，即式(14)迭代運算中的φ只為了求得更優的Λ，來用于融合進A中，而融合得到的A則代回式(7)求得最終的β。

于是假設多層極端學習機由兩層稀疏自動編碼器和一層基于最大相關熵準則的極端學習機構成，以批次數為3做例，將訓練數據平均分為3組，分別使用D1、D2、D3來表示。將D1輸入MCC-HELM1中，得到多層極端學習機決策層的隱含層輸出的特征矩陣Η31，并迭代求得第一部分訓練數據D1所對應的輸出權重矩陣β1；同理分別將D2、D3輸入MCC-HELM2、MCC-HELM3中，得到多層極端學習機決策層的隱含層輸出Η32、Η33。本文提出一種批量編碼式MCC-HELM的結構，對D組訓練結果進行融合決策。對于數據D1來說，根據2.1內容所示令：

H1=H31

A1=Λ1

其中Λ1表示數據D1通過半二次優化技術迭代求得的對角矩陣，則：

(15)

(16)

將第2批數據求解得到的特征矩陣Η32與第1批數據求得的特征矩陣Η31結合，得到Η2：

同時，通過式(14)的迭代得到Λ2，于是：

則得到：

(17)

式(17)右側求逆部分用M2表示，則：

(18)

式(17)右側非求逆部分可表示為：

(19)

于是得到：

(20)

同理，依次將每一批訓練數據對應的MCC-HELM決策層中隱含層輸出進行融合，得到MCC-HELM最終的迭代表達式：

(21)

式(21)中，t表示每一批數據的迭代次數，Z表示已輸入的數據批次數；每對一批訓練數據進行融合和學習，輸出權重矩陣β就被優化并更新一次，最終得到一個包含對所有訓練數據學習得到的信息的最優輸出權重矩陣βfinal.在測試階段，將測試數據全部輸入MMC-HELM中，得到Η3t.直接通過式(22)得到預測輸出：

Y=H3tβfinal

(22)

基于最大相關熵準則的批量編碼式多層極端學習機結構如圖2所示.

3 實驗仿真

本論文的數值計算得到了燕山大學超算中心的計算支持和幫助，均是基于Intel E5-2683v3(28核)@2.0GHz，64GB RAM，Centos7.2，使用Matlab R2018a仿真軟件進行的.以MNIST、NORB兩個深度學習最常用的大樣本數據集為例對本文所提出的BC-HELM進行參數的選擇并與其它多層極端學習機進行性能對比.其中MNIST數據集由250人的手寫數字圖像構成，是最常用的合理性檢驗數據集；NORB數據集為以不同照明及擺放方式攝制玩具模型的雙目圖像，是常用的圖像分類數據集.具體信息如表1所示.

3.1 參數選擇

圖2 基于最大相關熵準則的批量編碼式多層極端學習機結構圖Fig.2 Structure of batch coded hierarchical extreme learning machine based on maximum correntropy criterion

表1 數據集信息
Table 1 Data set information

數據集特征數訓練樣本數測試樣本數類別MNIST28?28600001000010NORB1024?224300243005

圖3 不同批次數性能對比Fig.3 Performance comparison of different batches

從圖3可以看到，對于最大內存占用：當批次數變大時，由于每次輸入的訓練樣本數變小，使得最大內存占用也會相應減小.對于運行時間：當批次數變大時，每次輸入的訓練樣本數變小，參與計算的矩陣維度減小，使得計算時間降低，但是同時，不同批次的訓練結果依次進行結合的過程需要額外的計算，因此隨著批次數的增加，這部分額外計算所需要的時間也將變大，因此，由于矩陣維度降低而縮短的計算時間大于多個訓練批次結合的計算時間時，運行時間將會下降，反之，運行時間將會上升.于是隨著批次數的增加，最大內存占用將呈現逐漸減小的趨勢，而整體運行時間將會出現先下降后上升的情況.因此需要通過實驗來折中選取每個數據集對應最佳的批次數，即最大內存占用盡量少的同時運行時間也較低的情況.圖3(a)對應NORB數據集將批次數依次設置為1-10時所占用的最大內存和運行時間，可以看出當批次數為5的點是最接近原點的點，即將訓練樣本分成5個批次進行訓練時，內存占用與運行時間都較低是最佳的情況.同時，由于測試樣本數相對較大(與訓練樣本數相同)，當批次數大于5時所占用的最大內存將產生于測試數據的運算過程中，因此呈現較為平緩的趨勢.圖3(b)對應MNIST數據集將批次數依次設置為1-10時所占用的最大內存和運行時間，當批次數大于6時，訓練樣本數降至10000以下，小于測試樣本數，所占用的最大內存將產生于測試數據的運算過程中，因此占用的最大內存趨于穩定，由于圖3(b)中當批次數為7、8、9、10對應的點相距較近，因此將這5種情況在表2中詳細列出進行對比與選擇.

表2 MNIST數據集的相近批次數性能對比
Table 2 Performance comparison of similar batches under MNIST data sets

批次數運行時間(S)標準差最大內存(MB)標準差778.009.833948.55379.46875.0012.543921.14716.08972.008.634190.761026.071070.007.033909.84243.19

表2中標準差數值的大小反映了每次運行的結果相對于均值的離散程度，標準差越小，表示運行結果與均值的偏差越小.通過表2不難發現，對于MNIST數據集，批次數為7、8、9、10時相比，最大內存占用相當，而批次數為10時的運行時間最短，同時運行時間與最大內存分別對應的數據標準差也最小.因此綜上所述，對于MNIST數據集將批次數設置為10，對于NORB數據集將批次數設置為5.將每個數據集的訓練批次數確定后，每批次輸入的樣本個數即確定了，在此基礎上通過實驗可以得到BC-HELM的正則化系數C的數量級以及決策層隱含層神經元個數L與測試精度之間的關系.實驗結果如圖4、圖5所示.

圖4 MNIST數據集 BC_HELM在不同參數下性能對比Fig.4 Performance comparison of BC_HELM with different parameters data set MNIST data set

從圖4可以看出，對于MNIST數據集，當C=220時(a)圖中的不同L值對應的曲線開始趨于穩定，同時從(b)圖中可以看出當L=8000時不同C值對應的曲線均達到最大值.即當L=8000時BC-HELM的精度在趨于穩定時達到最高，當L<8000時，測試精度隨著L的增加而變大；當L>8000時，測試精度略低于L=8000時的精度，且隨著L的增大，測試精度逐漸趨于穩定.從圖5可以看出，對于NORB數據集，當C=215時(a)圖中的曲線開始趨于穩定，同樣從(b)圖中可以看出當L=650時不同C值對應的曲線達到最大值.即當L=650時BC-HELM的精度趨于穩定時達到最高，當L<650和L>650時，測試精度隨著L的變化現象與MNIST數據集對應相同.于是對于MNIST數據集將BC-HELM的正則化系數C設置為220，決策層隱含層神經元個數L設置為8000；對于NORB數據集將BC-HELM的正則化系數C設置為215，決策層隱含層神經元個數L設置為650.

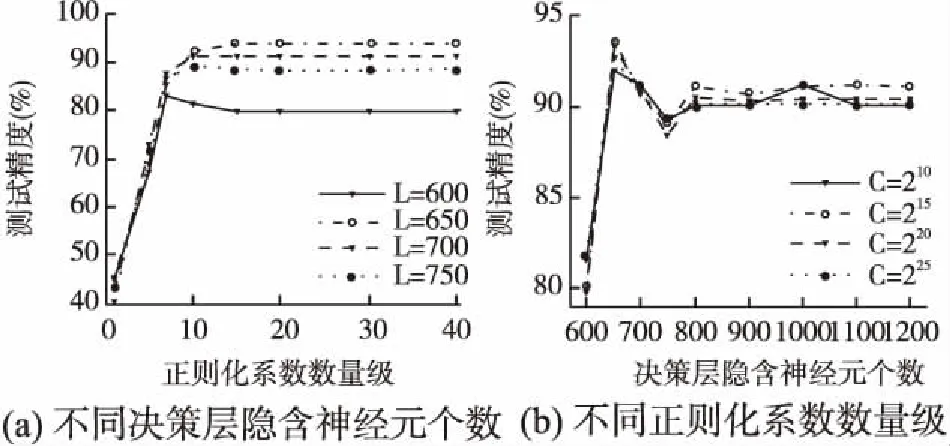
圖5 NORB數據集 BC-HELM在不同參數下性能對比Fig.5 Performance comparison of BC_HELM with different parameters under NORB data set

3.2 與HELM比較

將所有參數確定后，將BC-HELM與HELM進行性能對比.同時表3中列出了BC-HELM與HELM的多方面信息進行對比.

表3 BC-HELM與HELM的性能對比統計
Table 3 Performance comparison statistics between BC-HELM and HELM

數據集網絡運行時間(S)測試精度(%)最大內存(MB)決策層隱含節點數MNISTHELM[22]281.3799.1213234.3712000BC-HELM101.0099.526021.348000NORBHELM[22]432.1991.287618.8615000BC-HELM41.0093.592130.17650

根據表3中的統計數據可以得到，BC-HELM雖然與HELM有著相同的收斂特性，但相較與HELM，BC-HELM可以收斂于更高的測試精度.即與HELM相比，在MNIST數據集上測試精度提高0.4%，在NORB數據集上測試精度提高2.31%.這是由于MCC準則與HELM中MMSE準則相比降低了網絡對異常點的敏感性，使網絡的過擬合問題得到改善，因此測試精度有小幅度的提升.從決策層隱含節點數來看，訓練數據分批次輸入，使每次輸入的訓練樣本數減小，這直接降低了數據對決策層節點數L的需求，因此在兩個數據集上BC-HELM的決策層節點數均小于HELM.同理，對于占用的最大內存而言，BC-HELM與HELM相比，在MNIST數據集上降低54.50%，在NORB數據集上降低72.04%，這是由于輸入的訓練樣本數減小，相當于將特征矩陣縱向降維，同時決策層節點數減少相當于對特征矩陣進行橫向降維，雙重降維后對特征矩陣的計算量將大大減小，也因此與HELM相比運行時間被大大縮短，分別在MNIST數據集上縮短64.10%，在NORB數據集上縮短90.51%.綜上所述，BC-HELM相比于HELM，在保證測試精度的前提下，縮短了運行時間的同時大大降低了內存需求.

3.3 與其他多層ELM網絡對比

下面針對運行時間與測試精度兩個方面將BC-HELM與兩種經典的多層ELM網絡(文獻[22，1])以及三種最新的多層ELM網絡(文獻[12，3，2])進行對比，統計結果如表4所示.

表4 BC-HELM與其他多層ELM的性能對比統計
Table 4 Performance comparison statistics between BC-HELM and other multilayer ELM

數據集網絡運行時間(S)測試精度(%)MNISTAE-S-ELM[12]4347.0098.89EH-ELM[2]1632.4599.05FC-MELM[3]268.0098.89ML-ELM[1]475.8399.04HELM[22]281.3799.12BC-HELM78.0099.52NORBAE-S-ELM[12]2799.0091.24EH-ELM[2]1341.6791.78FC-MELM[3]498.0091.87ML-ELM[1]775.2988.91HELM[22]432.1991.28BC-HELM41.0093.59

從表4中數據可以得到，兩種經典的多層ELM網絡相比，HELM的運行時間在MNIST數據集上較ML-ELM縮短40.87%，在NORB數據集上較ML-ELM縮短44.25%，同時測試精度分別提高了0.08%和2.37%，這是由于在決策層中加入一層隱含層映射，使決策層變為原始極端學習機，相比于ML-ELM的決策層減少了自動編碼的大量計算因此運行時間被縮短，也正因加入的隱含層映射，將編碼層無監督學習到的結果映射至特征空間再進行有監督決策使測試精度提高，使HELM比ML-ELM具有更佳的學習性能.而3.2節中將HELM與本文提出的BC-HELM進行對比可以得到，BC-HELM具有比HELM更高的學習效率.

從三種最新的多層ELM網絡數據來看，AE-S-ELM、EH-ELM兩個網絡在兩數據集上的運行時間遠遠大于BC-HELM，較HELM也顯著增加，這說明此兩種多層ELM網絡均存在著由于網絡復雜度的增加而使運行時間被大幅增加的問題，而FC-MELM網絡的運行時間雖然與HELM相比不相上下，但BC-HELM與之相比，在MNIST數據集上縮短70.90%，在NORB數據集上縮短91.77%，可見從運行時間來看，BC-HELM最佳.從測試精度來看，在MNIST數據集上，BC-HELM較AE-S-ELM提高0.63%，較EH-ELM提高0.47%，較FC-MELM提高0.63%；在NORB數據集上，BC-HELM較AE-S-ELM提高2.35%，較EH-ELM提高1.81%，較FC-MELM提高1.72%，即與三種最新的多層ELM網絡相比BC-HELM的測試精度最高.綜上可得，本文提出的BC-HELM與兩種經典的多層ELM網絡以及三種最新的多層ELM網絡相比，運行時間更短且測試精度更高，具有更佳的學習效率.

4 結 論

本文構建了一種基于最大相關熵準則的批量編碼式多層極端學習機--BC-HELM.將MCC準則應用于HELM的決策層中，避免了傳統的MMSE準則對異常點敏感的問題，使HELM網絡的過擬合現象得到改善，從而保證了分類精度.同時提出了一種對訓練數據進行批量編碼的學習方法，通過將訓練樣本批量學習的方式，減少輸入網絡的樣本個數，降低了大樣本數據對網絡隱含層節點數的需求，使計算量隨之大大下降，從而也降低了學習過程中所占用的最大內存與運行時間.實驗結果表明，本文提出的BC-HELM與HELM相比，在保證測試精度的前提下，運行時間更短且內存需求也被大大降低；與其他多層ELM網絡相比也具有更高的學習效率.