面向不完備混合數據的矩陣增量知識維護方法研究

黃倩倩，李天瑞，楊 新，王國強，胡 節

1(西南交通大學 計算機科學與技術學院，成都 611756)2(西南交通大學 人工智能研究院，成都 611756)

1 引 言

1982年，波蘭學者Pawlak在經典集合論的基礎之上提出了粗糙集理論(Rough Set theory)[1，2].此后，該理論逐漸成為一種定量分析處理不精確、不一致和不完整信息與知識的有效數學工具.相較于模糊集和概率論等其他不確定性理論，粗糙集最大的優勢在于其不需要任何鄰域的先驗知識，就能有效地刻畫和分析不確定性問題.近30年來，粗糙集理論和方法已被廣泛應用于機器學習與知識發現、數據挖掘、模式識別和圖像處理等多個領域[3-7].

經典粗糙集模型通過一個等價關系(滿足自反性、對稱性和傳遞性)僅適用于處理名義型數據.這大大限制了粗糙集的適用范圍.大數據環境下信息的全面感知，使得所獲得的數據不再局限于某個單一的數據類型，其中名義型和數值型類型共存于的混合數據是最為普遍的現象.為了運用粗糙集理論處理混合數據，眾多學者開展了一系列的工作研究粗糙集的各種拓展模型.針對數值型數據，最為常見的做法就是將數值型數據進行離散化處理[8，9]，這就使得某些重要信息在轉化過程中丟失.因此，Lin等通過介紹了鄰域系統的概念，提出了鄰域粗糙集模型[10].Li等提出了基于鄰域的決策粗糙集模型用來處理包含噪聲的數值型數據[11].隨后，Hu等通過引入異構歐式重疊距離函數來刻畫同時具有名義屬性和數值屬性的對象之間的關系，提出了一種基于δ-鄰域關系的鄰域粗糙集模型[12].Chen等將偏序關系引入具有名義型屬性和數值型屬性的混合有序決策系統中，介紹了優勢鄰域粗糙集模型，并給出了面向混合數據的并行屬性約簡算法[13].近些年來，鄰域粗糙集模型已經吸引了眾多學者的注意并被廣泛應用于多個領域[14-17].

考慮到現實環境中數據采集過程中設備故障、存儲介質損壞、傳輸媒體堵塞和人為遺漏等因素，使得所收集的數據常常包含缺失值，即信息系統是不完備的.因此，如何高效地利用粗糙集理論和方法處理具有缺失值的信息系統已然成為當前知識發現領域中的一個研究熱點[18-25].在對于具有缺失名義型數據和數值型數據的混合信息系統的研究過程中，Jing等通過定義了新的距離函數，并結合概率的方法，提出了一種基于容差關系的變精度容差鄰域粗糙集模型[26]；Zhao等基于鄰域容差關系提出了一種擴展的粗糙集模型，并介紹了混合特征選擇方法[27]；與此同時，姚晟等提出了一種拓的不完備鄰域粗糙集模型，并構造了一種基于鄰域混合熵的不完備鄰域粗糙集屬性約簡算法[28]；黃恒秋等通過引入一種新的不確定距離度量函數，提出了基于聯系度距離函數的雙鄰域粗糙集模型[29].此外，錢文彬等基于一種新的完備鄰域容差關系，通過改進不可區分類的損失函數區間值的獲取方法，構建面向不完備混合信息系統的三支決策模型[30].

基于以上的研究工作，我們發現現今的不完備混合信息系統中缺失值的含義僅僅局限于某一種語義解釋，并不適合處理“不關心值”和“丟失值”共存的不完備混合信息系統.因此，本文將定義兩種新的鄰域關系，即鄰域特征關系和量化鄰域特征關系，并基于這兩種關系構建拓展的鄰域粗糙集模型，從而有效地處理不完備混合信息系統.此外，利用相關的矩陣和運算，介紹粗糙鄰域近似知識的矩陣計算方法.最后，當不完備混合信息系統中屬性隨著時間發生變化時，提出基于矩陣的增量知識維護機理和方法，這對豐富動態知識更新和知識獲取理論有著重要的意義.

2 相關知識

2.1 不完備信息系統

傳統粗糙集理論中，設四元組S=(U,A,V,f)是一個信息系統，其中，U={u1，u2，…，un}和A={a1，a2，…，al}分別表示非空有限的對象集合和屬性集合;V=∪a∈AVa為所有屬性值的集合，Va表示屬性a的值域;f:U×A→V為一個信息函數，即:對于任意u∈U和a∈A有f(u，a)∈Va.特別地，若A=C∪D，其中C和D分別為條件屬性集和決策屬性集，那么信息系統稱之為決策表.

定義1[1].給定一個信息系統S，對于任意子集Q?C，論域上關于Q的不可區分關系定義為：

RQ={(u，v)∈U2|?a∈Q，f(u，a)=f(v，a)}

(1)

顯然，不可區分關系RQ滿足自反性，對稱性和傳遞性，因此是一個等價關系.若存在a∈C和u∈U使得f(u，a)=*或f(u，a)=?，那么信息系統S被稱為不完備信息系統，其中“*” 和 “?” 分別表示 “不關心值” 和 “丟失值”.等價關系因其自身的局限性，并不能有效的處理不完備信息系統.因此，Grzymala-Busse提出了特征關系[23]，其可被視為容差關系[18]和相似關系[20]的一種泛化表現形式.

定義2[23].設S為不完備信息系統，對于任意子集Q?C，論域上關于Q的特征關系定義為：

KQ={(u，v)∈U2|?a∈Q，f(u，a)=?∨(f(u，a)=

f(v，a)∨f(u，a)=*∨f(v，a)=*)}

(2)

由上述定義可知，特征關系KQ僅僅滿足自反性，不一定滿足對稱性和傳遞性.對于任意一個對象u∈U，令KQ(u)表示u基于特征關系KQ的特征類，即KQ(u)={v∈U|(u，v)∈KQ}.

定義3[23].設S為不完備信息系統，?X?U，Q?C.則X基于特征關系KQ的上、下近似集分別定義為：

(3)

2.2 鄰域粗糙集

通過從拓撲空間中引入鄰域概念，Hu等提出了一個鄰域關系處理名義屬性和數值屬性共存的混合信息系統[12].給定一個信息系統S和一個閾值δ，?Q?C.對于任意一個對象u∈U，δQ(u)表示u關于Q的鄰域，即：

δQ(u)={v∈U|ΔQ(u，v)≤δ}

(4)

其中，Δ是一個距離函數(滿足正則性，對稱性和三角不等性).目前，Minkowski距離，作為一個重要的度量函數，已被廣泛應用于機器學習和模式識別領域，其定義如下：

(5)

當p=1時，稱為Manhattan距離；當p=2時，稱為Euclidean距離；當p=時，稱為Chebychev距離.

定義4[12].設S為一個信息系統，對任意子集Q=QC∪QS?C，其中QC和QS分別是名義型屬性集和數值型屬性集，論域上關于Q的鄰域關系定義為：

NQ={(u，v)∈U2|ΔQC(u，v)=0∧ΔQS(u，v)≤δ}

(6)

顯然，鄰域關系僅滿足自反性和對稱性，不一定滿足傳遞性.因此，對于任意對象子集X?U，X基于鄰域關系NQ的上、下近似集定義為：

(7)

2.3 不完備混合信息系統

定義5.設S=(U，A，V，f)是不完備混合信息系統，其中：

1)U={u1，u2，…，un}是非空有限的對象集合，稱為論域；

2)A=AC∪AS(AC∩AS=?)是非空有限的屬性集合，AC和AS分別為名義型屬性集和數值型屬性集；

3)V=∪a∈AVa，Va表示屬性a的值域；

4)f：U×A→V為一個信息函數，使得?a∈A，u∈U有f(u，a)∈Va；

5)存在某個屬性a∈A，使得f(u，a)=*或f(u，a)=?.

表1 一個不完備混合決策系統
Table 1 An incomplete hybrid decision system

Ua1a2a3a4du1210.52.0Nu2110.71.8Yu3?00.51.5Yu41?0.92.1Nu510?1.9Yu62?0.2?N

3 不完備混合信息系統中鄰域粗糙集模型

接下來，將介紹兩種新的鄰域關系(鄰域特征關系和量化鄰域容忍關系)來處理本文所提出的不完備混合信息系統.

3.1 鄰域特征關系

定義6.設S是一個不完備混合信息系統，對任意屬性子集Q=QC∪QS?A，論域上關于Q的鄰域特征關系的定義為：

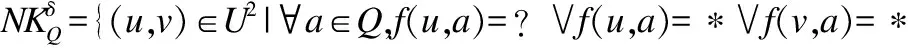
(8)

其中，δ為一個給定的閾值.

(9)

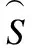
(10)

證明：

同理可證其余情況.

粗糙集理論中，近似分類精度是一個非常重要的評價指標，用于描述近似分類的不確定性度量.

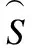
(11)

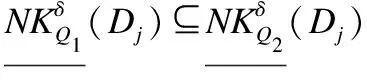
同理可證其余情況.

3.2 量化鄰域特征關系

受到數據驅動數據挖掘思想的啟發，Wang等提出數據驅動量化容忍關系處理由名義型數據組成的不完備信息系統[31].顯然，這種關系并不適合用來處理本文介紹的不完備混合信息系統.因此，基于數據驅動的思想，針對名義型數據和數值型數據，我們引入兩個新的度量函數，從而提出一個新的鄰域關系.

定義10.設S是一個不完備混合信息系統，A=AC∪AS.令ρC：U2×AC→和ρS：U2×AS→分別是關于AC和AS的兩個度量函數，具體定義如下：

(12)

和：

(13)

其中，λ1和λ1是閾值，且0≤λ1，λ2≤1.

表2 相關符號說明
Table 2 Description of related symbols

符號含 義a∈AC一個名義型屬性b∈AS一個數值型屬性Via(1≤i≤m1)關于屬性a的第i個已知屬性值Vjb(1≤j≤m2)關于屬性b的第j個已知屬性值Ha屬性a下所有屬性值為已知值的對象集合Hb屬性b下所有屬性值為已知值的對象集合sia集合{u∈U|f(u,a)=Via}的基數njb集合{u∈U|u∈Hb→|f(u,b)-Vjb|≤δ}的基數

定義10中所涉及的相關符號的具體含義可見表2.注意，?a∈AC，?b∈AS，函數ρC和ρS具有如下性質：

1.滿足正則性；

2.不一定滿足對稱性，如ρC(u1，u4，a2)≠ρC(u4，u1，a2)；

3.不一定滿足三角不等性，如令λ1=0.5，有ρC(u1，u6，a2)=ρC(u6，u4，a2)=0和ρC(u1，u4，a2)=，則ρC(u1，u4，a2)>ρC(u1，u6，a2)+ρC(u6，u4，a2).

因此，ρC和ρS被稱為偽度量函數.

定義11.設S是一個不完備混合信息系統，對任意屬性子集Q=QC∪QS?A，論域上關于Q的量化鄰域特征關系的定義為:

(14)

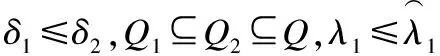
證明：證明過程與性質1的證明相似，故省略.

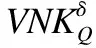
(15)

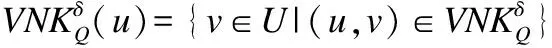
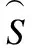
(16)

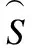
(17)

3.2 鄰域特征關系和量化鄰域特征關系之間的關系

基于上述兩種新的鄰域關系的定義，我們可以得到以下定理.

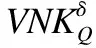
證明：

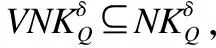
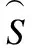
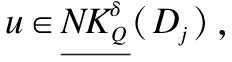
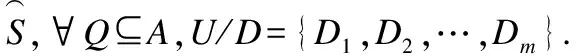
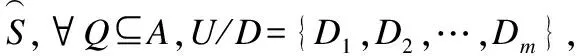
例2.表1給出了一個不完備混合決策系統，令δ=0.3和λ1=λ2=0.5.首先，基于決策屬性D，可得U/D={D1，D2}，D1={u1，u4，u6}和D2={u2，u3，u5}.其次，根據定義6有:

則可得關于D1和D2的一對近似集：

由定義8可得:

4 不完備混合信息系統中基于矩陣的近似集計算方法

通過引入決策矩陣、關系矩陣和相關的誘導矩陣，我們將介紹不完備混合信息系統中計算近似集的矩陣方法.

定義15.設U={u1，u2，…，un}為所有對象形成的集合，?X?U，則稱為X的特征向量，其中:

(18)

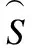
(19)

1)DM=[G(D1)，G(D2)，…，G(Dm)]；

證明：根據定義15和定義16，易知結論成立，故此省略證明過程.

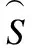
(20)

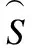
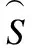
ΩQ=ΛQ·(MQ·DM)

(21)

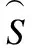
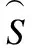
(22)

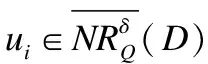
?φi>0

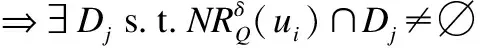
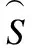
(23)

基于以上對不完備混合信息系統中基于矩陣運算的近似集構造方法的討論和分析，我們設計了一種計算近似集的靜態算法，即算法1.

算法1.不完備混合信息決策系統中基于矩陣的近似集靜態計算算法.

Step 1.fori= 1 ton/*構造決策矩陣DM的元素*/

forj=1 tom

if (ui∈Dj) then

dij=1；

else

dij=0；

end for

end for

Step 2.fori= 1 ton/*構建矩陣MQ和ΛQ*/

λi=0；

forj=1 ton

mij=1；

λi=λi+mij；

else

mij=0；

end for

end for

Step 3.fori= 1 ton

φi=0；

forj=1 tomdo

ωij=σij/λi；/*計算中間矩陣ΩQ*/

φi=max(φi，ωij)；/*計算基本向量ΦQ*/

end for

end for

ori= 1 ton

if (φi>0) then

if(φi==1)then

end for

例3.由表1所示，可知D1={u1，u4，u6}，D2={u2，u3，u5}，根據定義16有：

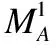
基于定義18，有：

因此，根據推論2可計算D1和D2的上、下近似集為：

根據定理2，可知:

5 屬性集變化時不完備混合信息系統中基于矩陣的近似集增量更新方法

5.1 屬性集增加的情形

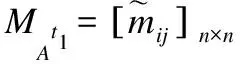
(24)

(25)

其中，“⊕”表示異或運算.

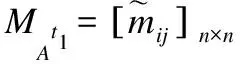
(26)

根據上述已給出的相關理論分析，我們設計了增加屬性集時基于矩陣的近似集增量更新算法，即算法2.

算法2.不完備混合決策系統中屬性動態增加時基于矩陣的近似集增量更新算法.

forj= 1 ton

if (mij==1) then

mij=0；

λi=λi-1；

fork=1 tom

σik=σik-dik；

end for

else

mij=1；

end for

end for

Step 2.fori= 1 ton

φi=0；

forj= 1 tomdo

end for

end for

fori= 1 ton

if(φi>0) then

if(φi==1) then

end for

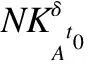
根據推論2，計算D1和D2的近似集為:

表3 屬性增加時不完備混合決策系統
Table 3 Incomplete hybrid decision system
with adding attribute

Ua1a2a3a4a5a6du1210.52.001.9Nu2110.71.82?Yu3?00.51.511.6Yu41?0.92.11?Nu510?1.921.5Yu62?0.2?01.6N

5.2 屬性集刪除的情形

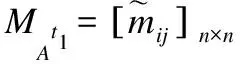
(27)

證明：證明過程與定理3的證明過程類似，故略.

(28)

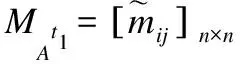
(29)

根據上述已給出的相關理論分析，我們設計了刪除屬性集時基于矩陣的近似集增量更新算法，即算法3.

算法3.不完備混合決策系統中屬性動態刪除時基于矩陣的近似集增量更新算法.

forj= 1 ton

if (mij==0) then

mij=1；

λi=λi+1；

fork=1 tom

σik=σik+dik；

end for

else

mij=0；

end for

end for

Step 2.fori= 1 ton

φi=0；

forj= 1 tomdo

end for

end for

fori= 1 ton

if (φi>0) then

if (φi==1) then

end for

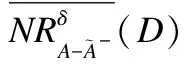
基于推論7，由關系矩陣誘導的對角矩陣被更新為：

再結合推論8和推論9，中間矩陣被更新為：

由推論2，可計算D1和D2的上、下近似集：

表4 屬性刪除時不完備混合決策系統
Table 4 Incomplete hybrid decision system
with deleting attributes

Ua2a3a4du110.52.0Nu210.71.8Yu300.51.5Yu4?0.92.1Nu50?1.9Yu6?0.2?N

6 結 論

本文以具有缺失名義型數據和數值型數據的不完備混合信息系統為研究對象，通過整合鄰域關系和特征關系的特點，提出了鄰域特征關系.與此同時，通過引入數據驅動數據挖掘的思想，進一步推廣了鄰域特征關系，定義了量化鄰域特征關系.基于這兩種關系介紹了兩種拓展鄰域粗糙集模型，并研究了其相關性質，豐富了鄰域粗糙集理論框架.此外，通過引入決策矩陣、關系矩陣等相關矩陣，介紹了基于矩陣的粗糙鄰域近似知識的計算方法.

隨著信息技術的快速發展，實際環境中所收集的數據總是呈現出動態性變化，如何利用已有的結果高效、及時地獲取知識已然成為亟待解決的問題.因此，針對不完備混合信息系統中屬性集的增加和刪除，提出了基于矩陣的增量知識維護機制，并通過具體的實例展現了所提出方法的有效性.在未來的工作中，利用UCI數據集測試增量更新方法的性能，以及通過運用云計算等并行技術來提高不完備混合信息系統中動態知識獲取方法的效率將是我們研究的重點.