具有五個相異素因子的某些奇正整數的刻畫
張四保
(喀什大學數學與統計學院,新疆 喀什 844008)
設N是正整數,σ(N)表示N的所有正因子的和函數。對于一個完全數N有σ(N)=2N。到目前為止只找到51個梅森素數[1],由梅森素數與偶完全數的特殊關系,從而也就確定了51個偶完全數,而尚未解決奇完全數存在性的問題。似乎由于在推翻奇完全數存在性這一問題上屢戰屢敗,眾多學者轉而定義了許多與之密切相關的概念,提出了大量的問題[2]。若σ(N)>2N,則N稱為盈數;若σ(N)<2N,則N稱為虧數;若σ(N)=2N+d,則N稱為盈度為d的盈完全數,當d=1時,N稱為準完全數;若σ(N)=2N-d,則N稱為虧度為d的虧完全數,當d=1時,N稱為殆完全數,以上d都是N的一個正真因子。對于以上概念的相關研究,可參考文獻[3-8]。
對于奇虧完全數,在文獻[8]中刻畫了滿足ω(N)≤2的所有虧完全數N的結構,其中ω(N)表示為N的相異素因子個數函數;在文獻[9-10]中給出了結論:不存在虧完全數N,其中N滿足ω(N)=3;在文獻[11-12]中給出了虧完全數N的一些性質刻畫,其中N滿足ω(N)=4。本文將通過初等方法來討論具有五個相異素因子的虧完全數的存在性問題。
1 結論及其證明
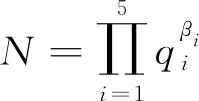
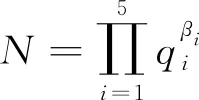
(1)
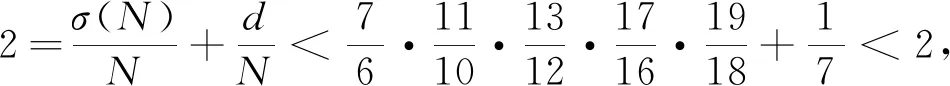

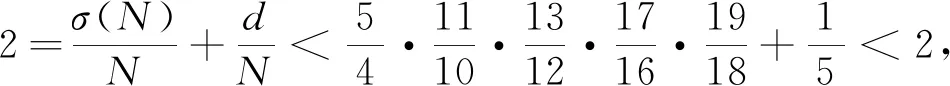
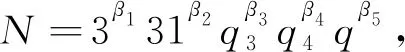
證明若q3≥41,則
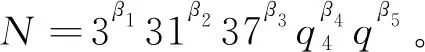
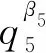
得出矛盾,則q5=43或者q5=47。
若d′≥9,則
得出矛盾。
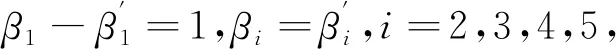
(2)
令
F1(β1,β2,β3,β4,β5)=
則由(1)式有
F1(β1,β2,β3,β4,β5)=G1(β1,β2,β3,β4,β5)
(3)
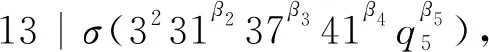
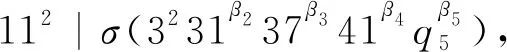
當q5=43,β1≥6時,有
F1(β1,β2,β3,β4,β5)=
這與(3)式相矛盾。
當q5=47,β1≥6時,有
F1(β1,β2,β3,β4,β5)=
這與(3)式相矛盾。定理2證畢。
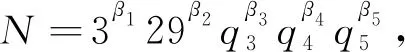
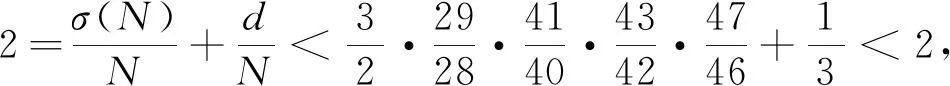
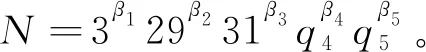
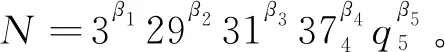
得出矛盾,則q5=41,43,47,53,59,61,67,71,73,79,83,89,97。
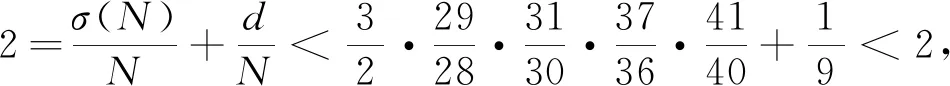
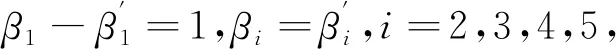
(4)
令
F1(β1,β2,β3,β4,β5)=
則由(1)式有
F1(β1,β2,β3,β4,β5)=G1(β1,β2,β3,β4,β5)
(5)
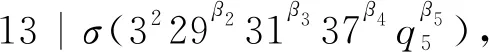
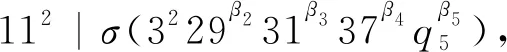
當β1≥4,q5=41時,有
F1(β1,β2,β3,β4,β5)=
這與(5)式相矛盾。
當β1≥4,q5=43時,有
F1(β1,β2,β3,β4,β5)=
這與(5)式相矛盾。
當β1≥4,q5=47時,有
F1(β1,β2,β3,β4,β5)=
這與(5)式相矛盾。
當β1≥4,q5=53時,有
F1(β1,β2,β3,β4,β5)=
這與(5)式相矛盾。
當β1≥4,q5=59時,有
F1(β1,β2,β3,β4,β5)=
這與(5)式相矛盾。
當β1≥4,q5=61時,有
F1(β1,β2,β3,β4,β5)=
這與(5)式相矛盾。
當β1≥4,q5=67時,有
F1(β1,β2,β3,β4,β5)=
這與(5)式相矛盾。
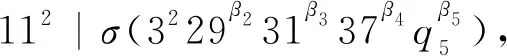
當β1≥6,q5=71時,有
F1(β1,β2,β3,β4,β5)=
這與(5)式相矛盾。
當β1≥6,q5=73時,有
F1(β1,β2,β3,β4,β5)=
這與(5)式相矛盾。
當β1≥6,q5=79時,有
F1(β1,β2,β3,β4,β5)=
這與(5)式相矛盾。
當β1≥6,q5=83時,有
F1(β1,β2,β3,β4,β5)=
這與(5)式相矛盾。
當β1≥6,q5=89時,有
F1(β1,β2,β3,β4,β5)=
這與(5)式相矛盾。
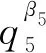
當β1≥8,q5=97時,有
F1(β1,β2,β3,β4,β5)=
這與(5)式相矛盾。定理3證畢。
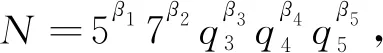
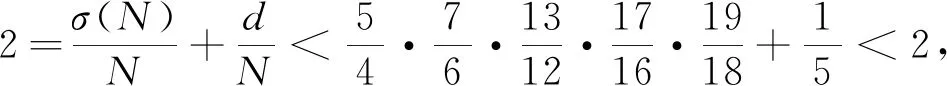
得出矛盾,則q5=17或者q5=19或者q5=23。
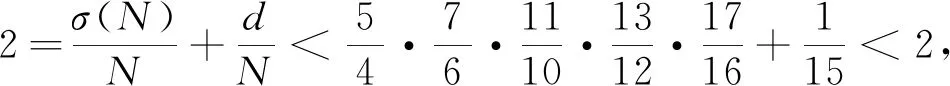
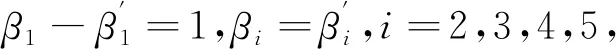
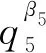
(6)
令
F1(β1,β2,β3,β4,β5)=
則由(1)式有
F1(β1,β2,β3,β4,β5)=G1(β1,β2,β3,β4,β5)
(7)
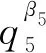
這顯然是不成立的。
當q5=17,β1≥4時,有
F1(β1,β2,β3,β4,β5)=
這與(7)式相矛盾。
當q5=19,β1≥4時,有
F1(β1,β2,β3,β4,β5)=
這與(7)式相矛盾。
當q5=23,β1≥4時,有
F1(β1,β2,β3,β4,β5)=
這與(7)式相矛盾。定理4證畢。
2 結語
對于定理2,定理3只是討論了定理1中q1=3時q2≤31中的兩個具體的情況,而定理4討論了定理1中的當q1=5的全部可能。如若將定理1中q1=3時q2≤31中的其他情況通過本文的討論方式給出相應的性質或結論,這將有助于解決是否具有五個相異素因子的奇虧完全數的問題。

