博弈論在無人機應急通信網絡研究中的應用

周韜瑒

（安徽工業大學管理科學與工程學院，馬鞍山 243032）

0 引言

蜂窩移動網絡已經經歷了2G、3G、4G通信，現在正往5G大步邁進。由于極速增長的通信速度，伴隨著各種各樣互聯網應用的產生，使得人們進入了互聯網時代。實時通信對人們帶來了極大便利，讓整個社會對網絡產生了極大的依賴。如果有一天通信中斷，所有與網絡有關的應用都將停止，這無疑會對我們的生產生活產生嚴重的影響。所以對于應急通信的研究成為移動通信研究中重要的一部分。無人機網絡現場評估對于控制災情、營救受災群眾以及災后重建具有重大意義，無人機網絡可以幫助救災指揮官識別、處理和掌握大型自然災害或其他緊急情況中的關鍵因素。此外，因其網絡建構價格便宜、對應用場地要求低、易于快速部署以及擴展性強等優勢，受到了越來越多研究人員的關注，因此，深入研究基于多無人機的無線應急通信網絡具有重要的實際意義和應用前景[1,2]。博弈論是研究具有競爭或者合作性質現象的理論與方法，它既是現代數學的一個新分支，也是運籌學的一個重要學科。博弈論最大的特點是能夠為相應的博弈過程找到一個納什均衡，有時候這個找到的均衡點也正是最優策略解，針對突發事件現場無線路由器自組織網絡的快速安置以及靈活組織，采用博弈論的理論與模型對以多無人機為中繼節點中的競爭與合作進行建模，使得我們對問題的研究找到最優策略。

1 博弈論的基本概念

1.1 博弈論的基本元素

博弈論起源于經濟學，它被用來模擬沖突或合作方的行為[3]。它提供了一種分析競爭參與者之間相互作用的方法，該方法已成功應用于進化生物學、政治、控制系統、通信和許多其他學科的問題。在博弈理論中，博弈的基本元素包括：參與人（Player）、策略（Strategy）、支付（或收益，Payoff）。博弈是由這些元素所組成的決策情況，當中每個元素都必須清楚明確，下面給出這些基本元素的定義。

（1）參與人。參與人也稱局中人，是指博弈中選擇行動最大化自己效用的決策主體。參與人是理性人，其目標是通過選擇某種策略以使自己的收益最大化。在博弈論中，我們常用Γ={1，2，…，n}表示一個n人博弈的所有參與者的集合，用i∈Γ代表博弈中的任何一位參與者。

（2）策略集。策略集中包含了參與者能夠選擇的所有策略，策略和行動是十分相似的兩個概念，策略可分為純策略和混合策略。策略是參與人在給定信息集的情況下選擇行動的一種規則，它規定參與人在什么情境下選擇什么行動，是參與者的“行動方案”。它是一項規則而非行動本身，每個參與人均有可供其選擇的多種策略。在一個n人博弈中，可以用si∈Si表示第i位參與者的一個特定策略，而Si則表示第i位參與者所有可選擇的策略的集合或策略空間。n位參與者各選擇一個策略形成n維向量s={s1,s2,…,sn}稱為策略組合。

（3）收益。參與者選擇某個策略時所能獲得的效用，每個參與者從各種策略組合中獲得的收益，由于它是策略組合s的函數，所以也稱為支付函數。一個n人博弈中，用 ui（s1,s2,….,si,….,sn）表示第 i位參與者的支付。博弈的基本特征是一位參與者的支付不僅取決于自己的策略選擇，而且取決于其他參與人的策略選擇。

1.2 博弈過程及結果描述方法

在博弈中，一個均衡就是一個由所以參與者的最優策略所組成的組合，即一個特殊的策略組合。給定其他參與人選擇的策略，每個理性參與人將選擇最大化自己的回報的策略。這就導致了一種平衡狀態，沒有任何參與者偏離其選擇策略的動機；這樣的舉動會減少該參與人的收益。這組選擇稱為納什均衡（NE）。Nash平衡是最流行的游戲解決方案概念。在理想的世界中，將有一套策略，每個玩家選擇一個動作，所有玩家的最佳反應都將重合。此狀態稱為“純策略納什均衡”（PSNE）。在真實情境中，并不總是有PSNE，但是在可能的策略范圍內存在概率分布。這種類型的NE被稱為“混合策略納什均衡”（MSNE）。直覺上來說，PSNE是MSNE的特例，為此，每個玩家的選擇之一的概率為1。在一個n人博弈中，如果為每個參與者給一個編號，那么便可以用si*表示第i位參與者的最優策略。而s*=（s1*,s2*,…,sn*）則是由所有參與者的最優策略所組成的策略組合，即是一個均衡。

在一個n人博弈中，參與人用集合N={1,2，…，n}來表示，而參與人在當前情境下能夠選擇的行動策略用集合S來表示，參與人i所選擇的策略用si來表示si∈S，那么 s*={s1*,s2*,…,sn*}為納什均衡，當且僅當對任意的 i∈N，存在：

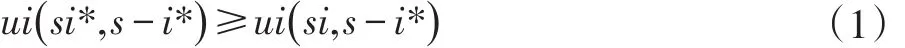
其中，s-i*表示除了參與人i以外其他參與人所選擇的策略，ui為參與人的最后收益，收益的計算是這些博弈中的關鍵階段。在有的情況下，博弈不存在納什均衡，同時，也在有的情境下，博弈可能存在不止一個納什均衡。

2 基于博弈論的無人機應急通信網絡

2.1 應急通信系統的發展狀況

目前國內比較成熟的應急通信系統主要集中于移動指揮車，如基于車載型移動應急指揮系統[4]。通過將移動指揮車以及移動接入點等部署到應急區域，從而搭建臨時無線通信網絡。同時，在國內面向公共突發事件情景下的應急機制的研究主要停留在傳統方法，如應急物資調度、應急設施選擇和路徑優化等[5]。除此之外，衛星網絡也是應急通信的重要手段，但主要由于其用戶擴展性差，這種通信主要用于指揮系統。眾多研究可以發現，當前研究成果不能適用于無基礎通信設備情景下用戶應急通信的要求。由于無人機體積小、操作簡單、成本低等特點，國內外眾多研究人員也提出基于多無人機的自組織網絡[6,7]。不同于傳統無線網絡或自組織網絡，基于多無人機的無線應急網絡，一方面需要根據用戶信息（終端用戶數量、通信量、位置信息等）的變化改變其網絡拓撲；另一方面，具有通信中轉功能的無人機，根據其他無人機的飛行路徑和通信要求，也需要改變其位置以保持無人機與無人機之間的連通性；于此同時，某些無人機還起到網關的作用，與原地基站建立通信鏈路，實現臨時網絡與外界網絡的聯系。

2.2 博弈論在無線通信領域的研究進展

博弈論是研究參與人如何進行策略選擇，以及這種決策如何達到均衡。博弈論最大的特點是可以為相應的博弈過程找到納什均衡點，有時候這個均衡點就是最優解，這樣，博弈論就能夠指導和分析無線通信網絡中的眾多算法設計。博弈論在無線通信網絡的應用已有大量的研究，其中主要的研究包括：功率控制、流量控制、擁塞控制、路由協議、網絡安全、協作中繼通信以及資源預留的競價等[8]。本文探討了基于無人機的無線路由器自組織應急通信網絡的關鍵技術，針對突發事件現場無線路由器自組織網絡的快速安置以及靈活組織，搭建出一種面向緊急突發狀況的以無人機為中繼節點的無線應急通信網絡體系結構，來滿足現場的應急指揮調度需求并且努力恢復用戶通信。將博弈論思想引進，探討無人機在當前體系下的移動機制問題。

2.3 無人機網絡最大生命期通信模型

如圖1所示的雙層無線網絡：路由層網狀（mesh）網絡和無人機網絡。前者由K個路由器和一些終端用戶組成，這是一種傳統的無線路由器網狀網絡。后者由U個無人機和一個遠程基站（例如：移動通信車輛）組成。無人機可以從路由器或其他無人機轉發數據，以實現災區內與外部終端用戶之間的通信。雙層網絡可以輕松快速地部署到災區，災難避難所、現場救援中心等，為終端提供緊急通信服務。研究的范圍是在路由器能量有限的條件下，無人機以以最快的方式收集數據，這是判定網絡性能的關鍵點。對于無人機而言，我們可以把無人機視為博弈中的參與人，無人機在飛行中共有8種可執行動作：東、西、南、北、東南、東北、西南、西北。無人機在某一位置的可飛行方向其實是圍繞自身360度方向，但我們只考慮8個方向的位置。那么這8個方向：東、西、南、北、東南、東北、西南、西北，便是無人機作為參與人的策略集。在這種情況下就變成了無人機與無人機之間的博弈，他們的收益就是無人機收集到的路由器的數據，同時，路由器都有能量的限制，無人機要在限制能量的條件下選擇最有利于自己的飛行路徑，即收益最大的策略，從而達到總體最優，即找到納什均衡點，無人機作為參與人可采取合作博弈的方式，以達到總體最優。

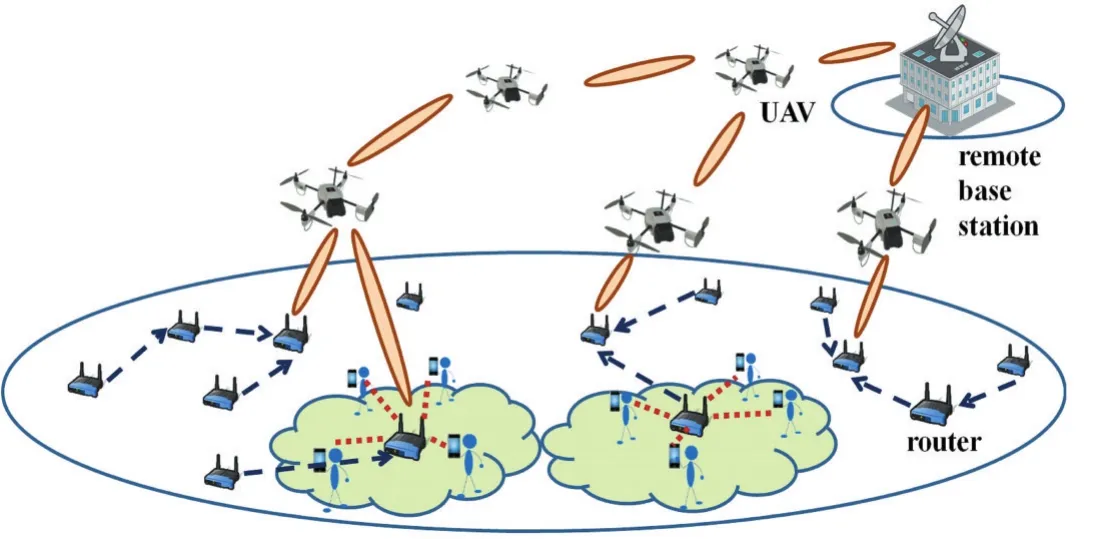
圖1

3 結語

通過介紹基于無人機的無線路由器自組織網絡，并對多無人機下如何以最快的方式收集數據。在利用博弈論解決該類問題時，要對如何達到一種均衡狀態進行研究。博弈論在分析無人機的無線路由器自組織網絡在為了最大化數據收集時的無人機移動選擇情況，為提出更加有效的策略選擇方案探索出有效且實用的方法。