《MATLAB基礎與應用》通識課程案例教學法探索

武文佳

摘要：文章以作者所講授的《MATLAB基礎與應用》通識課程為基礎，探討了MATLAB在優化問題、信號處理及經濟金融等領域中的應用，根據不同專業背景的學生，對本課程開展分組案例教學探索，以提高學生對MATLAB的應用能力。

關鍵詞：《MATLAB基礎與應用》;優化問題;信號處理;金融領域

中圖分類號：G642.0? ? ?文獻標志碼：A? ? ?文章編號：1674-9324（2020）10-0270-02

一、引言

MATLAB是在自然科學領域內廣泛應用的工程計算軟件，能夠掌握MATLAB的基本應用是大學生需要掌握的基本技能。在筆者所在院校，《MATLAB基礎與應用》作為通識選修課，每學期在全校學生范圍內開設，受到學生的普遍歡迎。MATLAB功能強大，命令與數學中的符號和公式非常接近，可讀性強，容易掌握。MATLAB根據專門領域的需要而設計了各種工具箱，可以解決多個學科領域的問題。為了更好地讓學生掌握MATLAB在專業中的應用，筆者根據不同專業背景的學生開展了案例教學法，讓學生按照專業分組進行案例學習。本文對MATLAB在不同專業領域的應用案例進行了研究。

二、MATLAB在優化問題中的應用

在自然科學和實際應用領域中，經常遇到優化問題的最優化方法就是研究如何從多個方案中合理的選取最優方案。如在庫存管理問題中，經常需要在保證銷量的前提下使庫存成本最小，在運送物資時設計運輸線路使得運費最少，等等，使得最優化問題的應用和研究深入自然科學的各個領域。MATLAB提供了優化工具箱，可以求解線性規劃、非線性規劃和多目標規劃等問題。下面對MATLAB用于非線性規劃給出一個案例。

案例1：設某人有200萬資金，要求3年內用完。若每年使用資金x（萬元），可得收益（萬元），若當年不用的資金可存入銀行，年利率為8%。制訂資金的使用計劃，使得3年收益總和最大。

求解：此問題為非線性規劃問題，用MATLAB解決非線性規劃問題的步驟是先定義目標函數和約束條件，設置優化參數，最后調用優化工具箱求解，MATLAB求解非線性規劃問題的函數是fmincon。

解決方案：先定義目標函數，設自變量為x，i=1，2，3，表示第i年使用的資金，則因變量y=++，題目所述問題則化為自變量x，i=1，2，3取何值時，目標函數y最大的問題，由于目標函數為非線性函數，因此屬于優化問題中的非線性規劃，其次研究約束條件，本題的約束條件為：（1）x≤200;（2）1.08x+x≤216;（3）1.1664x+1.08x+x≤233.28;（4）x≥0，i=1，2，3。

用MATLAB求解本題過程如下：

step1：定義目標函數function myfun=youhua（x）

myfun=-（sqrt（x（1））+sqrt（x（2））+sqrt（x（3）））

step2：主程序：youhuawenti.m

x0=[1;1;1];

A=[1 0 0;1.08 1 0;1.1664 1.08 1];

B=[200;216;233.28]

[x，fval]=fmincon（@youhua，x0，A，B）

程序運行結果如下：

x=

61.6067

71.8581

83.8152

fval=

-25.4810

結果表明用MATLAB可以很容易解決上述優化問題，第一年使用資金61.6067萬元，第二年71.8581萬元，第三年83.8152萬元時效益之和最大，最大效益為25.481萬元。

在授課中向學生講解MATLAB在優化問題中的應用，可以讓學生認識到MATLAB在實際生活中的應用，以提高學生學習的積極性以及分析解決問題的能力，這對學生專業課的學習和創新極其重要。

三、MATLAB在信號處理中的應用

信號處理是很多工科專業必學的專業基礎課，MATLAB在數字信號處理中也有廣泛的應用。數字信號處理把實際問題中的信號用符號表示成序列，通過信號處理設備，用數字數值計算方法處理，提取有用信息用于實際應用中。數字信號處理在圖像處理、通信工程、網絡工程等領域內都有廣泛的應用。MATLAB提供了信號處理的工具箱，包括信號處理工具箱、小波分析工具箱、通信工具箱等，可以滿足學生在實際專業課中的需求。信號處理工具箱提供了信號處理的基本函數，如square、sawtooth、tripuls、gauspuls等函數，也提供了信號變換函數和濾波器的設計函數，如fft、dct、FIR、IIR等，可以方便地解決信號變換和濾波器的設計分析等問題。下面給出一個實例：

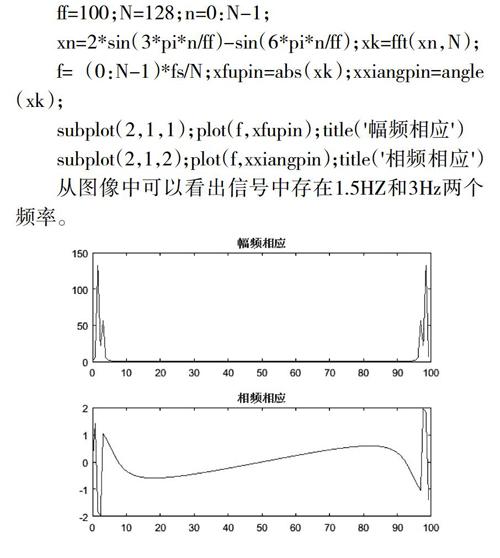
案例2：模擬信號x（t）=2sin（3πt）-sin（6πt），求其幅度譜和相位譜。

求解：問題2是典型的信號處理問題。首先對模擬信號進行抽樣，然后將離散時間信號截為有限長序列，利用快速傅里葉變換fft函數得到頻域值，則可獲得其幅度譜和相位譜。程序和圖像如下。

ff=100;N=128;n=0：N-1;

xn=2*sin（3*pi*n/ff）-sin（6*pi*n/ff）;xk=fft（xn，N）;

f=（0：N-1）*fs/N;xfupin=abs（xk）;xxiangpin=angle（xk）;

subplot（2，1，1）;plot（f，xfupin）;title（'幅頻相應'）

subplot（2，1，2）;plot（f，xxiangpin）;title（'相頻相應'）

從圖像中可以看出信號中存在1.5HZ和3Hz兩個頻率。

MATLAB在數字信號處理中還有很多其他應用，通過案例教學引發學生的學習興趣，學生可將MATLAB應用在專業中，達到學以致用、解決問題的目的。

四、MATLAB在經濟和金融領域中的應用

MATLAB在經濟和金融方面提供的工具箱包括經濟工具箱、金融工具箱、固定收益工具箱等，全面提供了財務分析、投資組合、商品評價、風險管理以及經濟模型建立的工具。其中經濟工具箱提供了經濟審計數學建模的函數，金融工具箱提供了財務分析等方向的函數，固定收益工具箱提供了經濟證券固定收益建模分析的函數等。在授課中面向經管學院經濟與金融專業的學生講解相應工具箱是極其必要的，也是學生在實際學習和工作中迫切需求的。下面舉一個實際應用中的簡單實例。

案例3：設投資者有兩種資產，總價值2億元，資產權重為35%和65%，資產的日波動均值為0.003和0.005，標準差為0.03和0.01，兩種資產的相關系數為0.7，置信度為0.98，求該資產在30天的投資組合風險值。

求解：本問題為一個典型的金融問題，可以利用金融工具箱中計算投資組合風險值函數portvrisk來求解。在授課時，可以先讓學生通過MATLAB強大的幫助功能分組自學，通過help portvrisk首先自學此函數，然后教師講解本函數的調用方式，其調用格式為：ValueAtRisk=portvrisk（PortReturn，PortRisk，RiskThreshold，PortValue）將問題中的數值作為上述函數的輸入參數，簡單計算可得該資產的投資組合風險值為0.123億元。

五、總結

本文根據筆者所在學校應用型本科院校的培養目標和學生的實際情況，從《MATLAB基礎與應用》課程的案例教學內容上進行了探討。對于本課程開展案例教學，可以增強學生對MATLAB的應用能力，提高學生對本課程的學習興趣，并會將所學內容運用到自身專業中和后續的工作中。

參考文獻：

[1]蔡旭暉，劉衛國，蔡立燕.MATLAB基礎與應用教程[M].北京：人民郵電出版社，2016.

[2]張志涌，楊祖櫻，等.MATLAB教程[M].北京：北京航空航天大學出版社，2015.

[3]卓金武，魏永生，秦健，李必文.MATLAB在數學建模中的應用[M].北京：北京航空航天大學出版社，2011.