基于圍線積分引理的信號變換域分析方法*

陳紹榮，何 健，陳柏良，薛在陽

（1.陸軍工程大學通信士官學校，重慶 400035；2.軍委裝備發展部軍事代表局駐成都地區軍事代表室，四川 成都 610041；3.深圳市惟新科技股份有限公司，廣東 深圳 518000；4.奧特斯科技（重慶）有限公司，重慶 401133）

0 引 言

早期的《信號與系統》著作[1-2]涉及復平面上的圍線積分引理，由于對圍線積分引理條件的敘述不嚴謹，因此使用時缺乏可操作性，在查閱有關《復變函數》著作[3]及近期的《信號與系統》著作[4]的基礎上，證明了圍線積分引理，基于圍線積分引理，研究了s域卷積運算問題，給出了利用區左極點或區右極點計算s域卷積的留數方法；依據連續時間非周期信號的ILT導出了非周期序列的IZT，基于圍線積分引理，給出了利用區外極點計算有終序列的IZT及計算z域卷積的留數方法，提出了利用兩個連續時間信號各自的雙邊LT來計算時域卷積信號及積信號相應樣值序列的雙邊ZT的方法。

1 圍線積分引理

設CR是s平面上半徑為|s|=R的圓周，CABC是CR上的任意一段圓弧，如圖1所示。

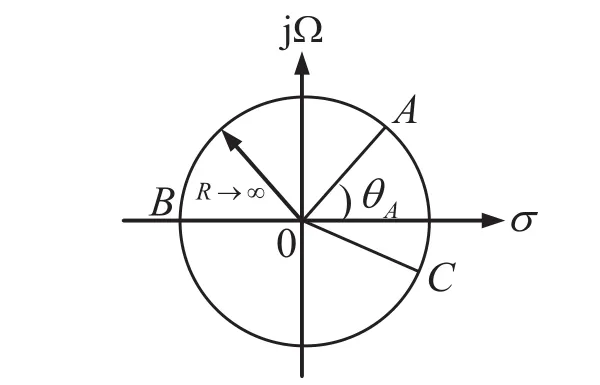
圖1 s平面上圍線積分引理示意圖

若函數F(s)在圓弧CABC上連續，并且滿足條件：

則有：

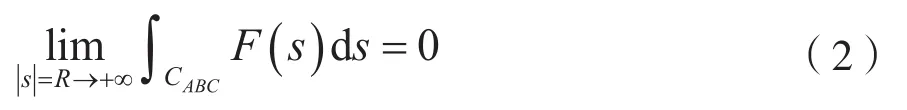
證明：

在圓弧 CABC上，令 s=Rejθ，則 ds=jRejθdθ，因為，所以對任意ε＞0，存在充分大的正數R0，當|s|=R＞R0時，則有：

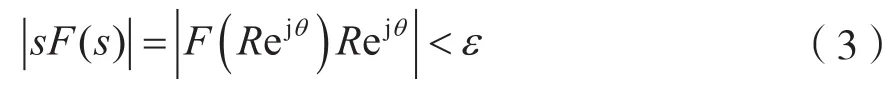
考慮到式（3），則有：

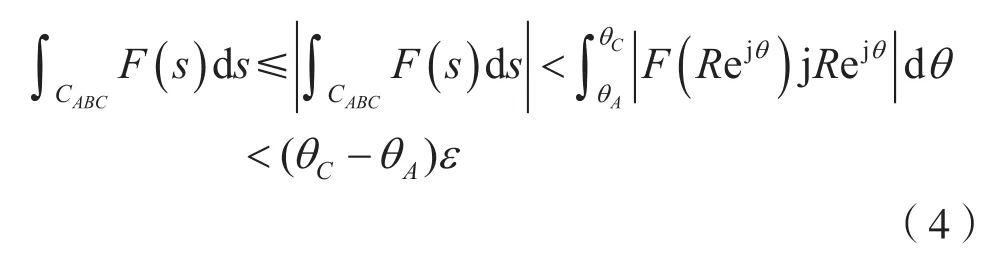
由式（4）可知，式（2）成立。

結論1：

若函數F(s)在CR上連續，并且則有：

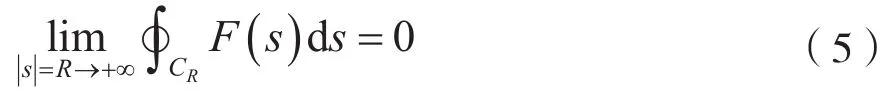
2 基于圍線積分引理的信號變換域分析方法

2.1 基于圍線積分引理及留數定理計算s域的卷積積分

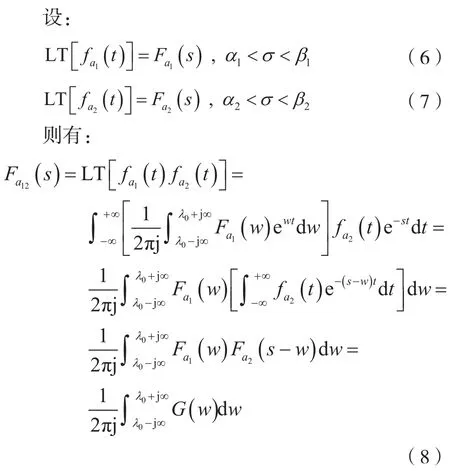
式中，G(w)=Fa1(w)Fa2(s-w)，w=λ+jΩw，s=σ+jΩ，考 慮 到 α1＜λ＜β1，α2＜σ-λ＜β2， 則 α1+α2＜σ＜β1+β2。λ0位 于 G(w)的 收 斂 域 λ1＜λ＜λ2之 內， 其 中，λ1=min(α1,σ-β2)，λ2=min(β2,σ-α2)。

設CR是w平面上半徑|w|=R的圓周，CABC（CADC）是CR上的逆時針（順時針）方向的一段弧，如圖2所示。

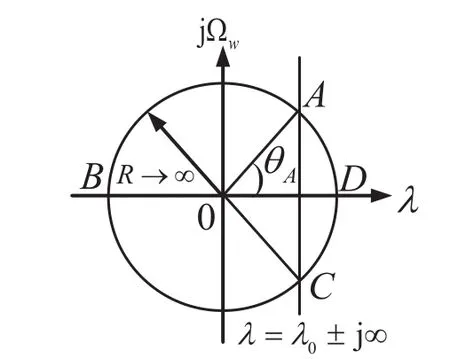
圖2 w平面上圍線積分引理示意圖

由圍線積分引理可知，若函數G(w)在CR上連續，并且滿足條件：

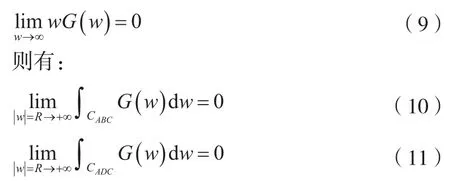
考慮到式（10），則式（8）可對G(w)的區左極點wi(i=1,2,…,p1)（Re[wi]≤λ1的極點），利用留數定理進行計算，即：

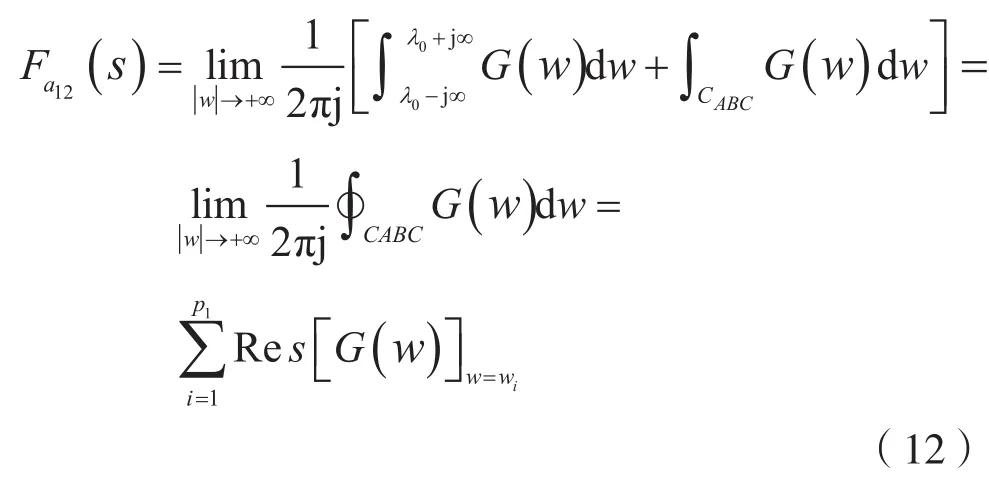
考慮到式（11），則式（8）也可對G(w)的區右極點wj(j=1,2,…,p2)（Re[wj]≥λ2的極點），利用留數定理進行計算，即：

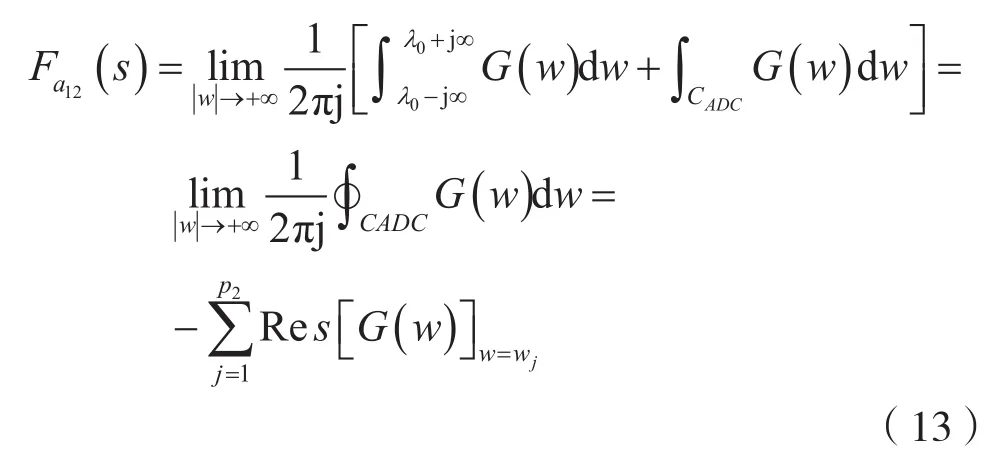
式（13）中的負號是由于圍線繞行方向為負向（即順時針方向）的緣故。

若G(w)的區右極點數目較少時，適宜用式（13）進行計算，否則，適宜用式（12）進行計算。

2.2 基于圍線積分引理及留數定理計算IZT

考慮到：

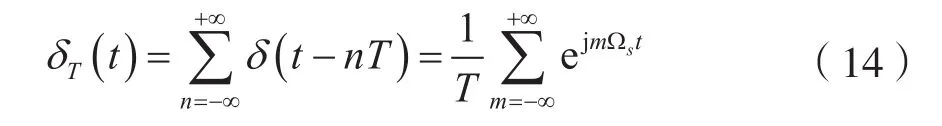
式中，Ωs=2π/T。

對連續時間信號fa(t)抽樣，其樣值信號f^(t)可寫成：

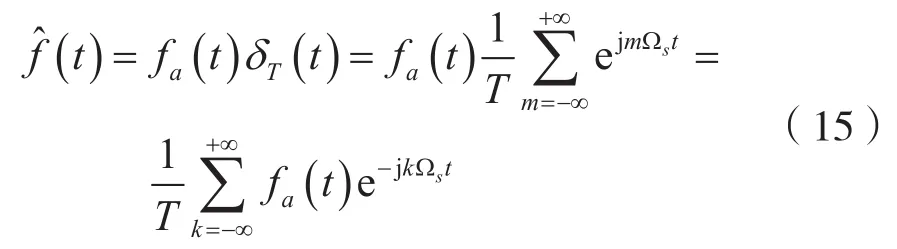
設：

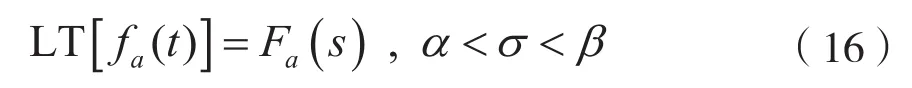
考慮到式（16），對式（15）兩邊取雙邊LT，可得：

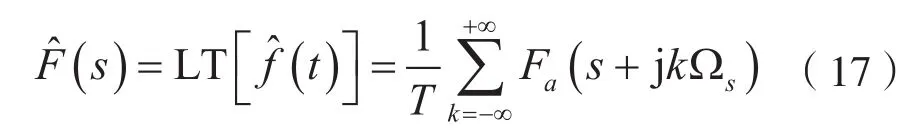
其實，式（17）還可寫成：

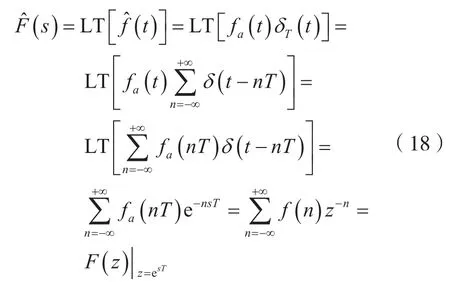
式中，f(n)=fa(nT)，z=esT，并且：

稱F(z)為序列f(n)的z變換（ZT），也稱F(z)為序列f(n)的象函數。

考慮到連續時間信號fa(t)的雙邊LT的象函數Fa(s)的收斂域為α＜σ＜β，因為z=esT，所以象函數F(z)的收斂域為 Ra=eαT＜|z|＜eβT=Rb。并將 F(z)的 |z|≤Ra的極點稱為區內極點，將F(z)的|z|≥Rb的極點稱為區外極點。

考慮到式（17），由式（18）可以得到：

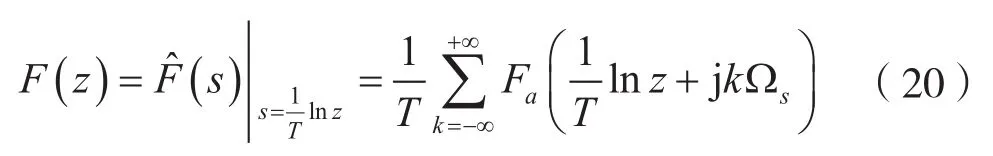
考慮到式（20）及拉普拉斯逆變換（ILT）式，則有：

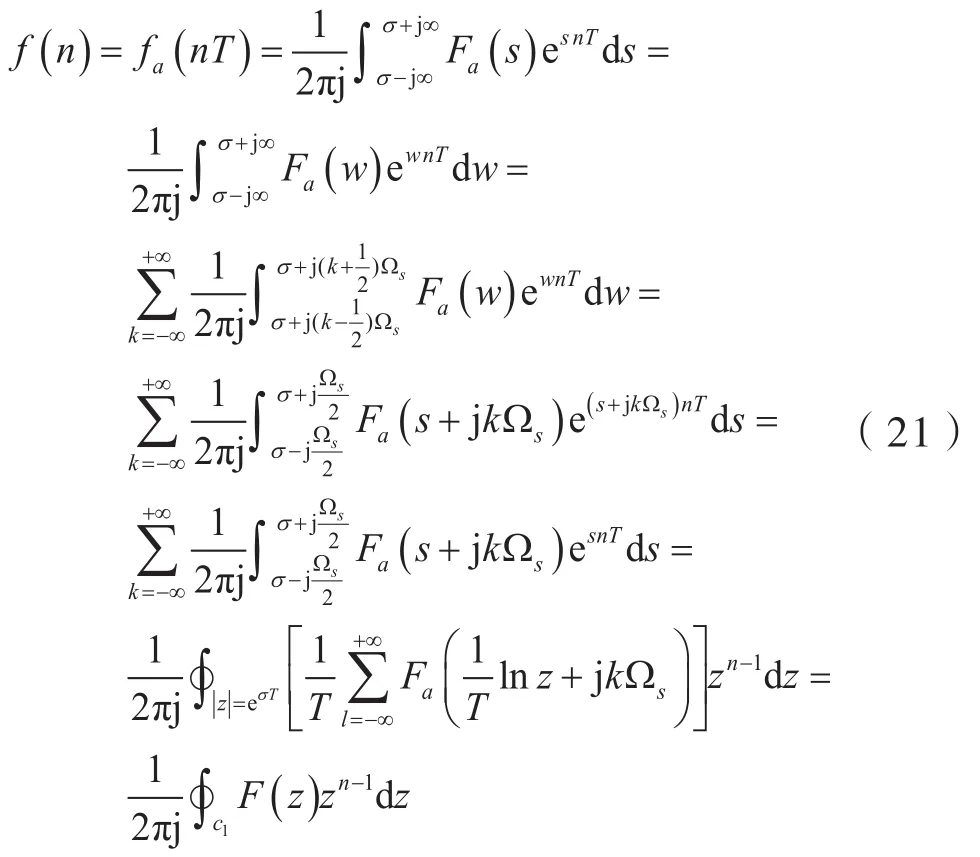
式（21）稱為象函數F(z)的逆z變換(IZT)，其中，c1為T(z)=F(z)zn-1的收斂域內的正向閉曲線。

先在z平面上F(z)的收斂區域Ra＜|z|＜Rb內畫一條正向圓周曲線c1，再引入一條半徑為無窮大的圓周曲線c2，最后選取一條將T(z)=F(z)zn-1的所有區外極點zp包括在內的積分路徑，如圖3所示。

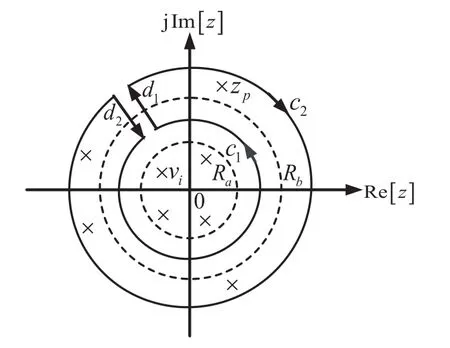
圖3 z平面上極點的圍線積分路徑示意圖

設

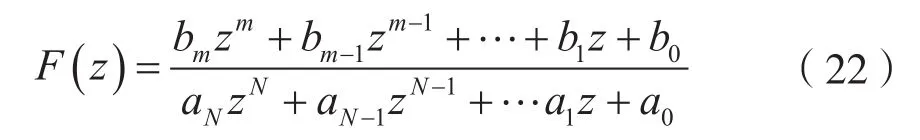
式中，ai(i=0,1,2,…,N)和bj(j=0,1,2,…,m)為常數。

令q=N-m，T(z)=F(z)zn-1，若n≤q-1，即q-n≥1時，則有：

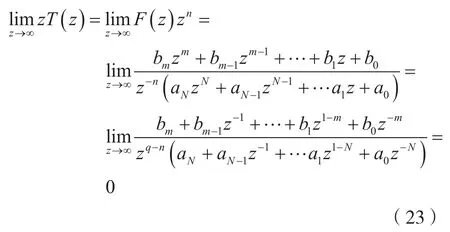
由于式（23）滿足圍線積分引理的條件，因此，有：

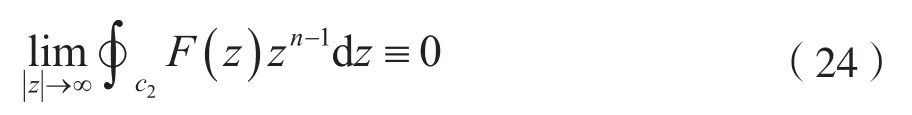
由圖3可知，對區外極點zp(p=1,2,…,n2)作逆z變換時，沿閉曲線積分的路徑由4段構成，它們分別是c1、c2、d1及d2。因為d1+d2線段的積分恒等于零，由式（24）可知，沿著c2的積分也恒等于零，于是逆z變換(IZT)可用下式計算，即：

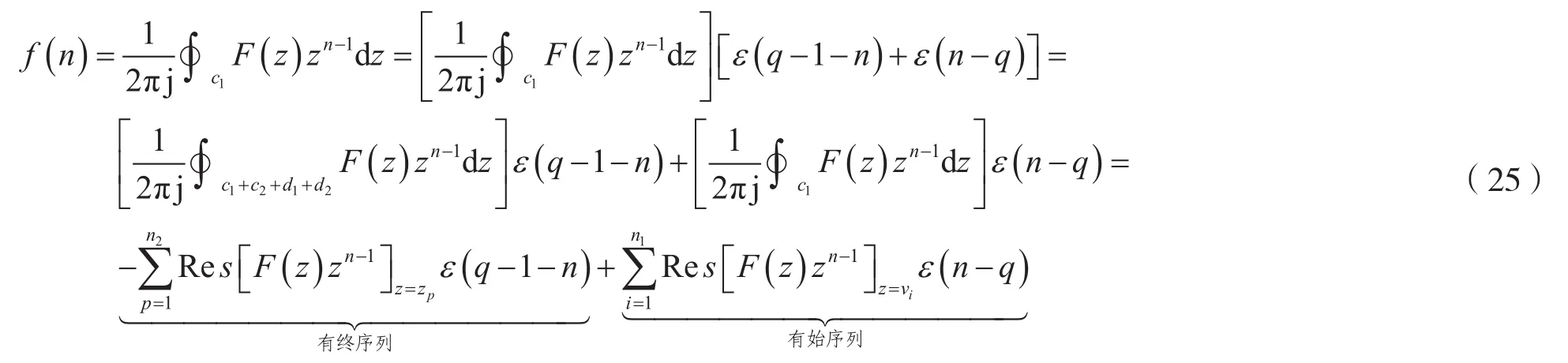
式中，ε(n)為單位階躍序列，zp(p=1,2,…,n2)是T(z)=F(z)zn-1的區外極點（即T(z)在正向閉曲線c1外的極點），n2為區外極點數目，負號是因所有的區外極點zp始終在積分路徑c1右側的緣故；vi(i=1,2,…,n1)是T(z)=F(z)zn-1的區內極點，n1為區內極點數目。

2.3 基于圍線積分引理及連續時間信號的雙邊LT確定相應序列的雙邊ZT

考慮到拉普拉斯逆變換式，則式（19）可寫成：

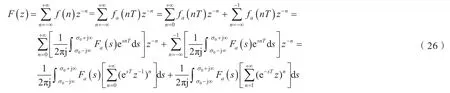
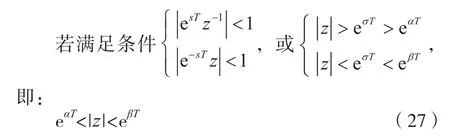
則式（26）可寫成：

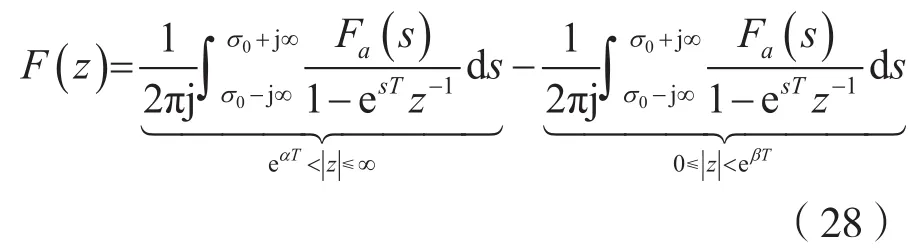
可見，式（28）中的第一部分僅與Fa(s)的區左極點（Re[s]≤α的極點）有關；第二部分僅與Fa(s)的區右極點（Re[s]≥β的極點）有關。

其實，計算式（28）的復變函數積分，還是非常困難的，下面假設Fa(s)是真分式，進一步研究式（28）的復變函數積分問題。

在s平面上，以s=0為圓心，作一半徑為R的圓周CR，與路徑σ=σ0±j∞(α＜σ0＜β)交于 A點和 C點，CABC（CADC）是CR上逆時針（順時針）方向的一段弧，如圖4所示。

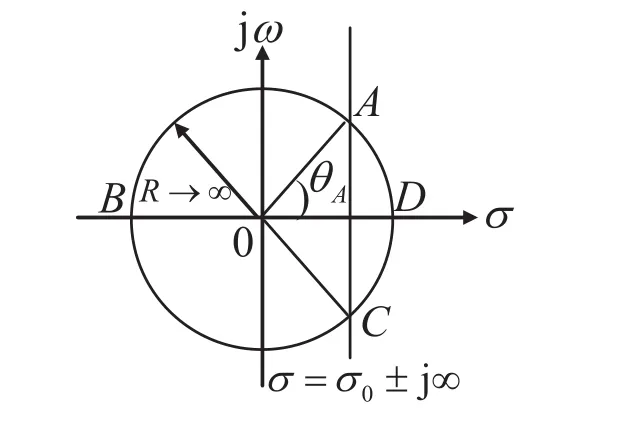
圖4 s平面上圍線積分路徑示意圖

令：

顯然，式（30）滿足圍線積分引理條件，于是，有：

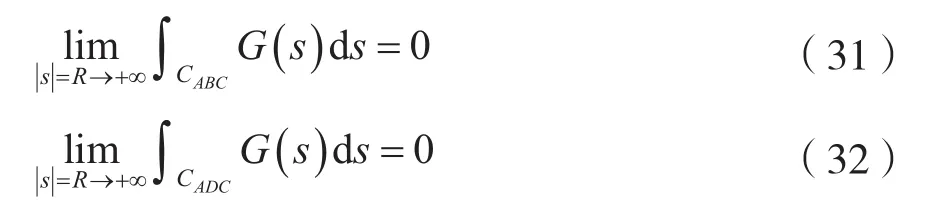
考慮到式（31）及式（32），則式（28）可寫成：

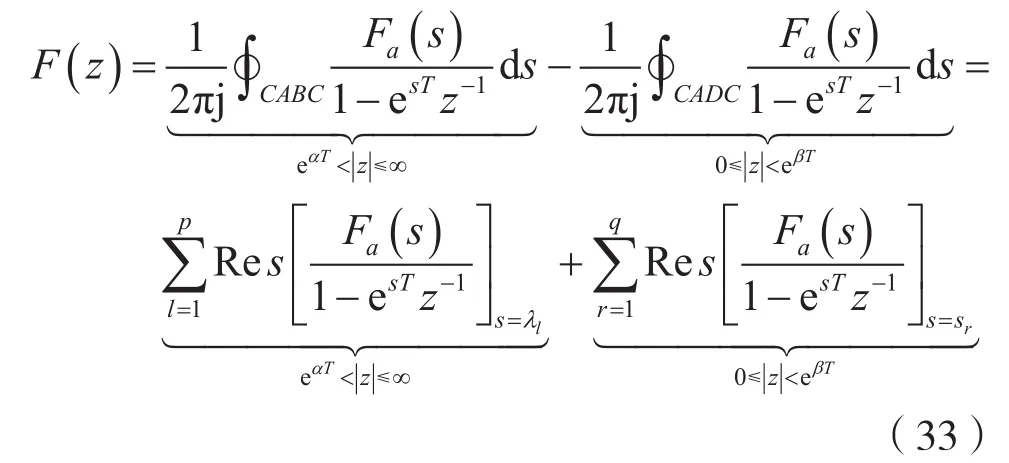
式中，s=λl(l=1,2,…,p)是Fa(s)的第l個區左極點（Re[λl]≤ α 的 極 點），s=sr(r=1,2,…,q)是 Fa(s)的第r個區右極點（Re[sr]≥β的極點）。

結論2：

式（33）揭示了一種直接利用連續信號的雙邊拉普拉斯變換來計算相應樣值序列的雙邊z變換的方法。

討論：

（1）設

考慮到式（6）及式（7），對式（34）兩邊取雙邊LT，可得：

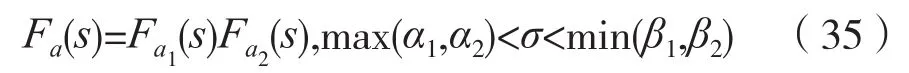
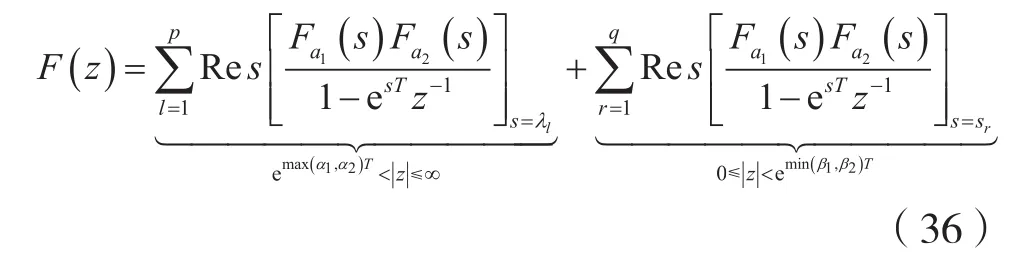
結論3：

式（36）揭示了一種直接利用兩個連續信號各自的雙邊拉普拉斯變換來計算卷積信號相應樣值序列的雙邊z變換的方法。

（2）設

考慮到式（8），對式（37）兩邊取雙邊LT，可得：

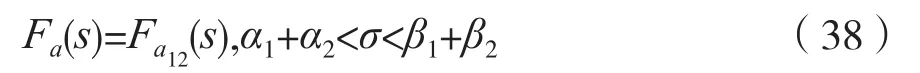
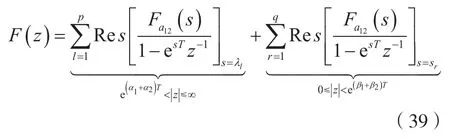
結論4：

式（39）揭示了一種直接利用兩個連續信號各自的雙邊拉普拉斯變換來計算積信號相應樣值序列的雙邊z變換的方法。

2.4 基于圍線積分引理及留數定理計算Z域的卷積積分

由式（37）可知，對連續時間信號fa(t)抽樣，其樣值序列可寫成：

積序列f(n)=f1(n)f2(n)的z變換除了利用式（39）進行計算外，還可用下述方法進行計算。

考慮到式（40）、式（20）、式（38）及式（8），則有：

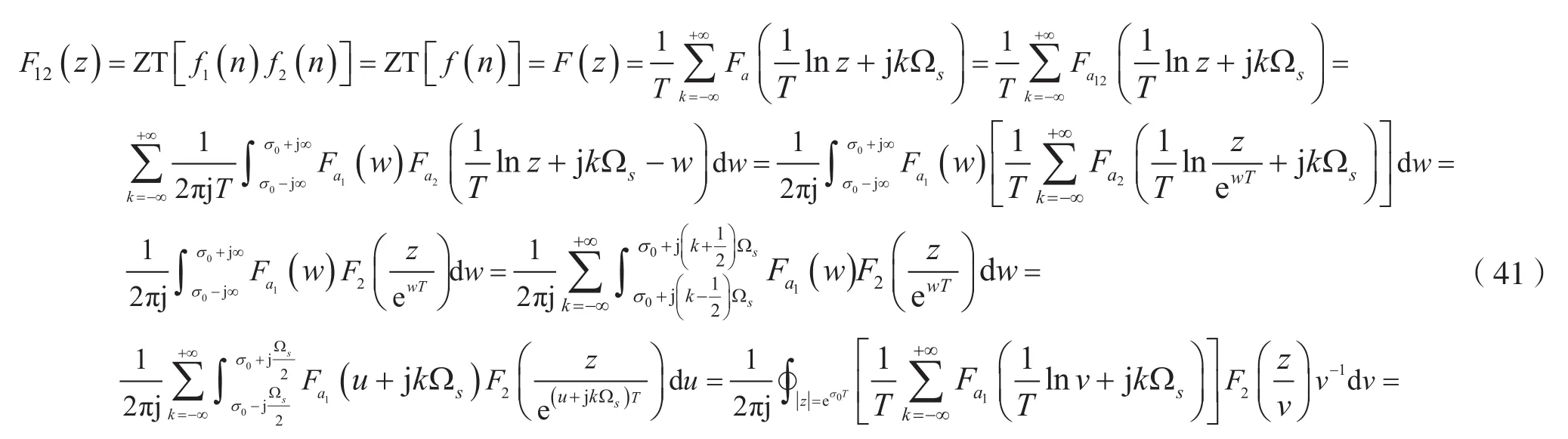
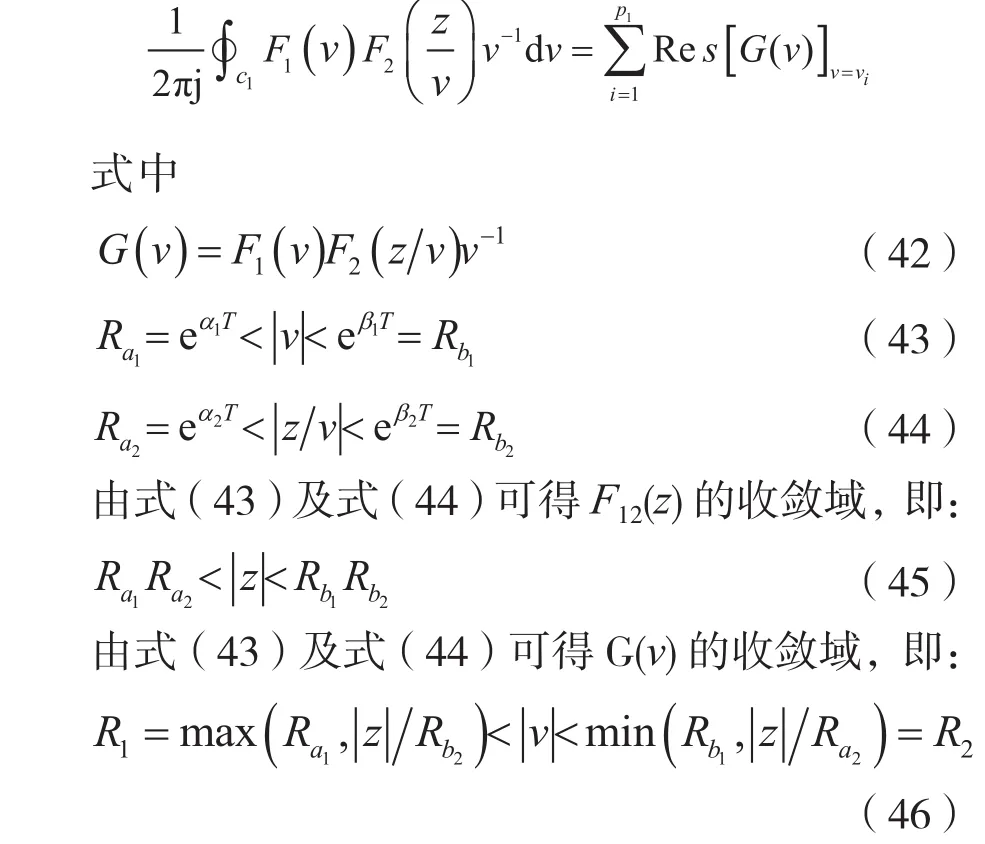
vi(i=1,2,…,p1)為G(v)在v平面上的區內極點，即|vi|≤max(va1,|z|/Rb2)的極點。

假設vj(j=1,2,…,p2)為G(v)在v平面上的區外極點，即的極點。為了利用G(v)的區外極點來計算F12(z)，先在v平面上G(v)的收斂區域R1＜|v|＜R2內畫一條正向圓周曲線c1，再引入一條半徑為無窮大的圓周曲線c2，最后選取一條將G(v)的所有區外極點vj均包括在內的積分路徑，如圖5所示。

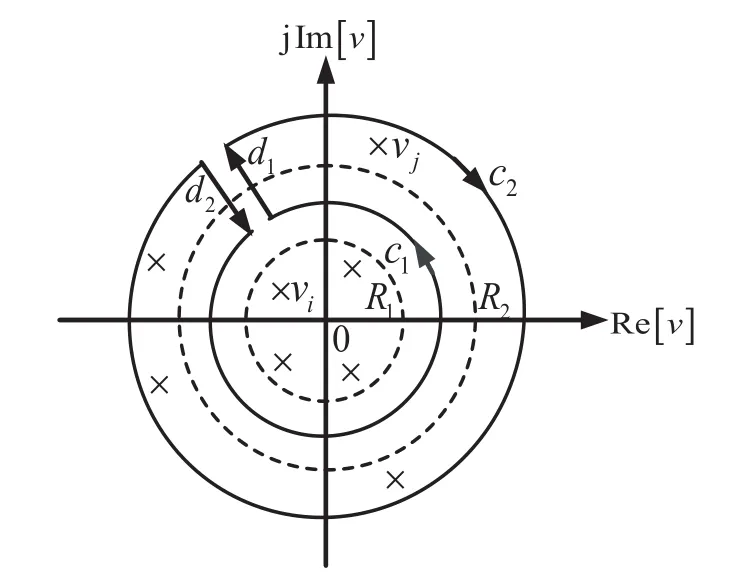
圖5 v平面上極點的圍線積分路徑示意圖

若滿足條件圍線積分引理條件：

則有：

由圖5可知，G(v)對區外極點vj(j=1,2,…,p2)作閉曲線積分時，沿閉曲線積分的路徑由4段構成，它們分別是c1、c2、d1及d2。因為d1+d2線段的積分恒等于零，由式（48）可知，沿著c2的積分也恒等于零，于是，有：

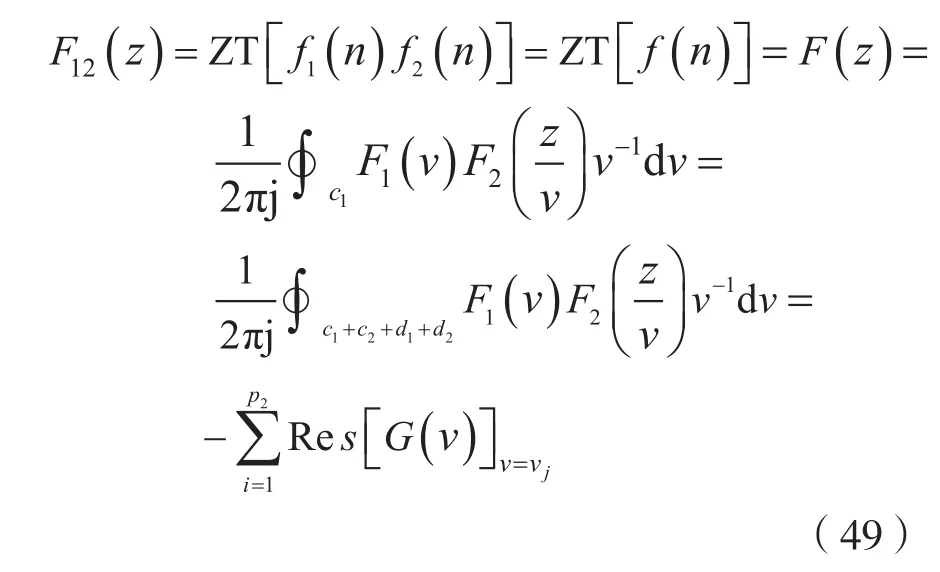
式中，G(v)=F1(v)F2(z/v)v-1，vj(j=1,2,…,p2)是 G(v)的區外極點，負號是由于圍線繞行方向為負向（即順時針方向）的緣故，F12(z)的收斂域仍為

當G(v)的區外極點數目較少時，適宜用式（49）進行計算，否則，適宜用式（41）進行計算。

例：設象函數

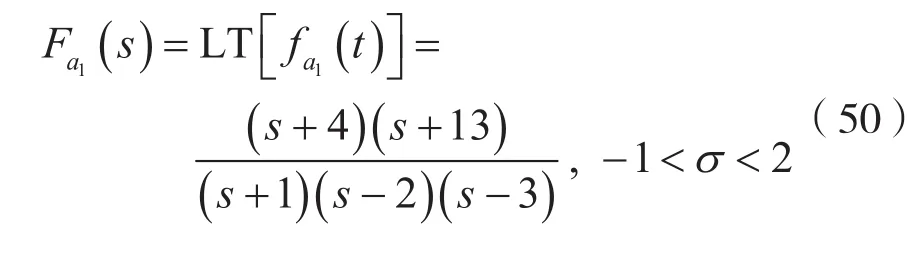
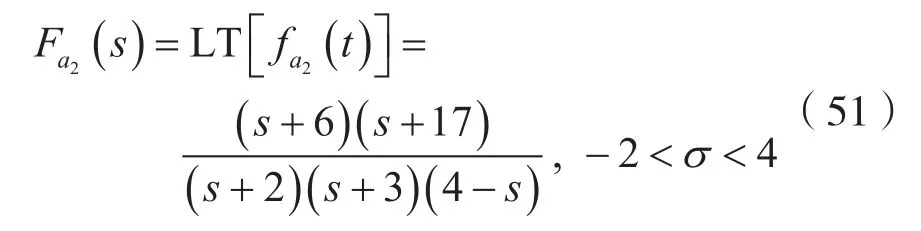
解：（1）考慮到式（50）及式（51），則有：

由式（57）及式（58）可知，G(w)有2個區左極點w=-1，w=s-4；有4個區右極點w=2，w=3，w=s+2，w=s+3，由式（12）可得：

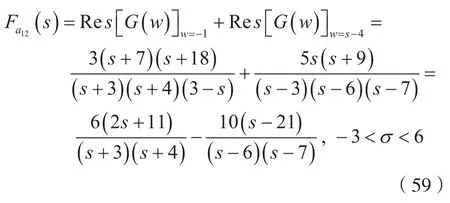
（2）方法1：

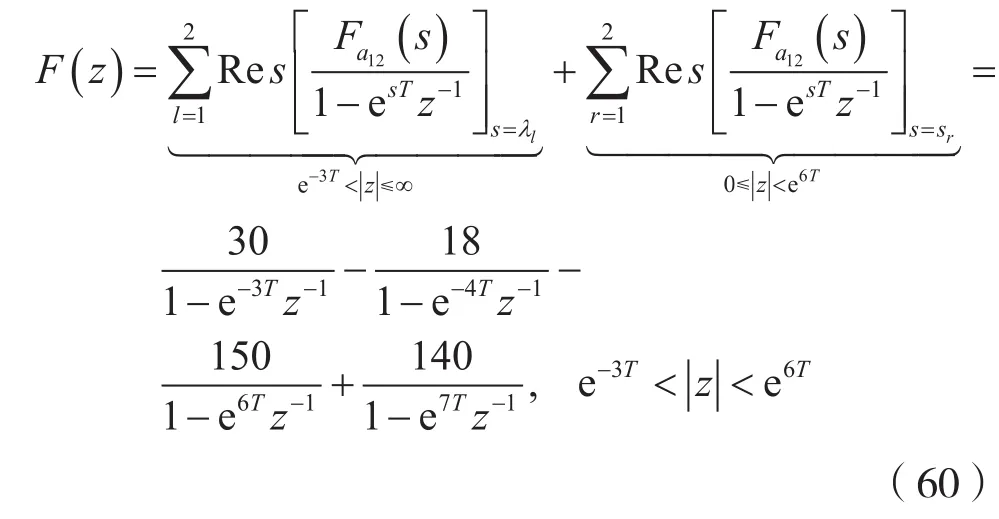
方法2：

由式（63）可得：

顯然，式（64）滿足圍線引理條件。

由式（68）及式（69）可知，G(v)有2個區內極點v=e-T，v=e-4Tz；有4個區外極點v=e2T，v=e3T，v=e2Tz，v=e3Tz，由式（41）可得：

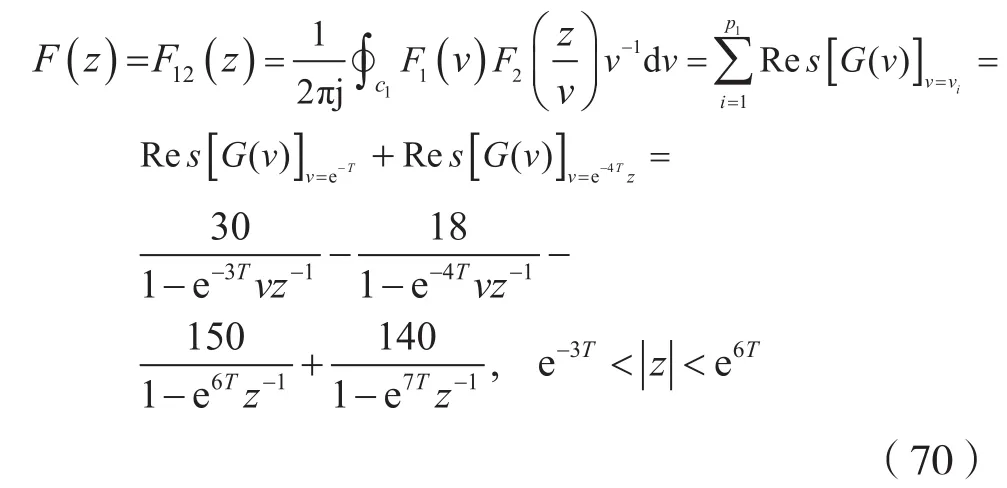
（3）考慮到

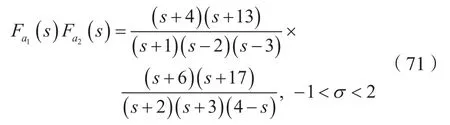
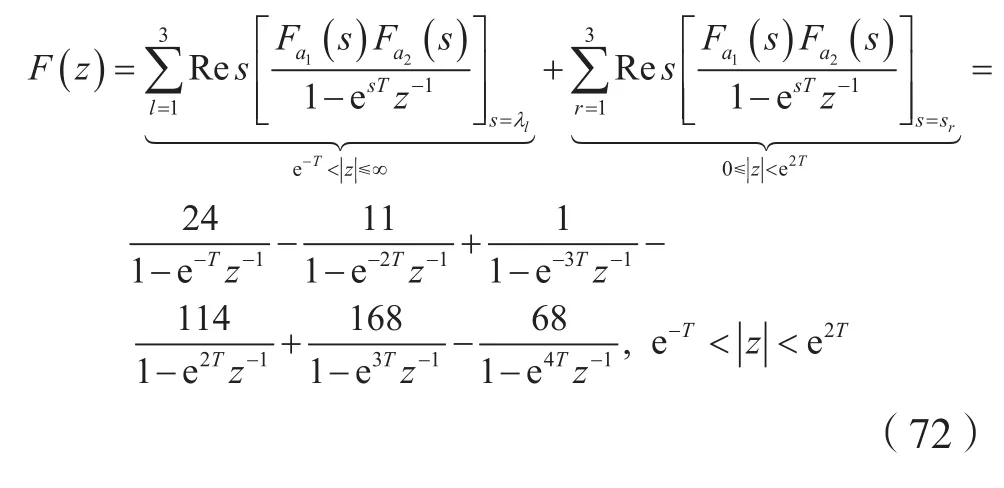
3 結 語

本文基于圍線積分引理，給出了利用區左極點或右極點計算s域卷積的留數方法；依據連續時間非周期信號的拉普拉斯逆變換導出了非周期序列的逆z變換，基于圍線積分引理，給出了利用區外極點計算有終序列的逆z變換及計算z域卷積的留數方法；提出了一種直接利用連續時間信號的雙邊拉普拉斯變換來計算相應樣值序列的雙邊z變換的方法，并分別給出了利用兩個連續信號各自的雙邊拉普拉斯變換來計算時域卷積信號及乘積信號相應樣值序列的雙邊z變換的方法。