面向服務器登錄日志的入侵檢測聚類算法分析比較研究*

張艷 羅文華 中國刑事警察學院

引言

網絡技術的迅速發展催生了大量新興的網絡犯罪，而服務器入侵屬于網絡犯罪中偵破難度較高的犯罪形式之一。在非法入侵計算機信息系統類案件的偵破中，通過聚類算法分析服務器登陸日志是電子數據取證領域必不可少的技術方法之一。

聚類是根據樣本數據之間的相似性進行分類并聚合的過程。在大數據時代數據挖掘已經成為大數據分析中最為核心的模塊，而數據挖掘依賴各種聚類算法。聚類算法會概括出海量數據中每一類的特點，以便針對某一個特定的類做進一步的分析。聚類還作為數據挖掘算法中的預處理步驟服務于其他分析算法。在數據挖掘算法中使用聚類算法可以準確地在海量數據中挖掘具有極高價值的信息，比如在網絡攻擊案件中可以幫助取證調查人員從海量日志數據集[1]中區分正常行為與入侵行為，進而挖掘破案線索或定案證據。入侵檢測中最重要的調查對象之一即是網絡服務器中的用戶登錄日志，為此本文以該類日志為數據基礎，針對K-means、DBSCAN以及改進的MajorClust三種常用的聚類算法進行分析，通過實驗結果比較三種算法的特點及不足，希望能夠為打擊日益猖獗的網絡攻擊犯罪提供可行高效的建議。

一、K-means算法

（一）算法簡介

K-means聚類[2]是最著名的分區聚類算法，是使用最廣泛的算法之一。其主要思想是給定一個對象集合和需要的聚類數目K，根據距離函數反復把對象分入K個聚類中。

（二）算法的原理及特點

K-means方法用于將雙向雙模對象（即對每個P變量進行N個對象的測量）劃分為K類（C1， C2， …，CK），其中Ck是聚類簇K中的所有對象集合，并且K是給定的。如果XN*P= {xij}N*P表示N*P的對象矩陣，則K-means方法構造這些聚類簇使得任何對象的行向量與其各自聚類簇的聚類中心向量之間的歐幾里德距離為至少與剩余聚類簇的聚類中心距離一樣小。

K-means原理簡單且實現容易，但K值通常依賴先驗知識、假設和實踐經驗的臨時決策。當數據具有多個維度時即使群集分離良好，選擇K也會變得更加困難。如果使用多個中心對象來描述從一種模式中提取的對象，則這些中心對象是對整體對象不必要的復雜描述，并且實際上多個中心對象捕獲關于子集的真實性不如一個中心對象。

二、DBSCAN算法

（一）算法簡介

DBSCAN算法[3]是基于密度的聚類算法。同一類別的對象之間是緊密相連的，通過將緊密相連的對象劃為一類就會得到一個聚類簇。該算法適用于處理大型數據集，并且能夠識別具有不同大小和形狀的群集。

（二）算法的原理及特點

DBSCAN算法以密度為度量將對象聚類。對于樣本集D=(x1， x2， ...，xm)，鄰域參數（領域半徑，領域半徑內對象的最小數量），實現xn∈ D且N(xj)≥MinPts，其中領域半徑、領域半徑內對象的最小數量需指定，xj為隨機對象，xn的 集合為N(xj) ，N(xj) 是隨機對象xj領域內對象的聚類簇。

DBSCAN算法可以對任意形狀的對象集進行聚類，執行效率高，且僅需輸入領域半徑和領域半徑最小數量即可實現快速聚類。但是該算法的領域半徑較難指定，領域半徑代表著對象間的緊密程度，決定著聚類效果的優劣。領域半徑內的點數量代表聚類結果中對象的最小數量，需經過多次嘗試。

三、改進的MajorClust算法

（一）算法簡介

MajorClust算法是基于密度的聚類算法，能夠自動進行對象聚類，通過計算對象相似度來改變聚類的形狀以提升聚類效率。

（二）算法的原理及特點

MajorClust算法將相似度作為聚類的依據，其處理結果顯得較為粗糙。實驗中，在原有基礎上改進MajorClust算法，根據“最大吸引制勝”原則[4]，以相似度為量度將對象迭代傳到聚類結果中。擁有“其鄰居的相似度之和的最大值”的對象與其最大相似度的對象實現聚類，其遵循的公式如下：

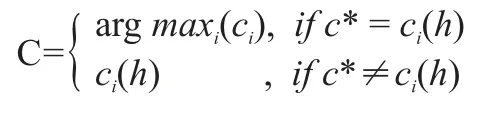
其中c是當前聚類簇，h是具有最大相似度的鄰居對象，并且c(h)是h的聚類簇標簽，ci是第i個聚類簇，c*是具有最大相似度的聚類。通過這樣的部署使得對象將僅跟隨最相似的對象。實際實驗過程中，將選取相似度之和最大的對象，以逐步挑選最相似對象，同時改進的MajorClust算法即選取了最長子串優化聚類效果。

MajorClust算法無需輸入參數，即可自動實現對象集的聚類，使得前期工作更為簡潔。在聚類推導過程中，由于只考慮對象的鄰居對象，從而擁有了良好的運行效率，同時使得對象最大程度的貼近從而精確了聚類簇的中心內容。該算法雖迭代次數有限，但在逐步選取相似度之和最大的對象時會因對象集數量的龐大而影響到運行時間。

四、實驗結果及比較

本實驗使用的樣本數據來自安裝Linux系統的服務器保存的登錄日志文件“auth.log”。該日志中的每條數據記錄由日期（date）、時間（time）、進程名稱（process name）、ID（PID）、主機名稱（hostname）以及具體的事件（event）組成。

采用聚類算法K-means、DBSCAN以及改進的MajorClust實現日志中數據的聚類，為分析事件類型、挖掘深層信息奠定基礎[5]。由于日志數據集過大，為了使聚類圖顯示更加直觀，選取日期為Nov 30的數據進行聚類實驗。

（一）數據處理

針對樣本數據聚類之前需要進行數據的預處理，即相似度計算。不同的相似度計算算法適應的數據類型也不盡相同。本實驗的樣本數據為以條為單位的文本數據記錄，故選用TF-IDF和余弦距離來計算相似度。

在相似度計算過程中，由于語句中的停用詞會導致其相似度偏高，因此實際聚類過程中設定停用詞并在數據記錄中去除，將“for”、“by”、“form”、“[preauth]”、“port”、“sshd”、“ssh”設定為停用詞并在計算相似度之前去除。

（二）三種算法實驗比對

算法結束后將對聚類效果進行準確性計算，其計算步驟如下：

（1）聚類中心：計算聚類中心不唯一的簇占實驗數據集的平均比例。

（2）聚類簇中內容：當聚類簇中出現少于一半的數據內容與簇中其他數據內容不相同時，計算其在該簇中所占的比例；若多于一半數據內容不相同，計算其占實驗數據集的比例。

（3）計算精確值：初始聚類效果準確性為100%，減去步驟1、2中的不準確性得到最終聚類效果準確性的精確值。

1. 使用K-means算法進行聚類

（1）確定K值，并隨機選擇K個聚類中心數據：K值代表聚類的簇數，K個聚類中心數據即K個簇的中心內容。日志文件為登錄類型的文件，決定選取4和5作為K值分別進行實驗。K值確定之后，將從所有樣本數據中隨機選擇K個數據作為聚類中心。

（2）數據劃分：遍歷樣本數據，以數據預處理獲得的相似度為衡量標準，將每條數據分給其對應相似度最高的聚類中心。若出現某條數據與所有聚類中心的相似度都為零的情況，則將此數據記錄分配給第一個聚類簇。

（3）更新聚類中心：在數據劃分后，將每一個簇中出現頻率最高的數據記錄更新為聚類中心。

（4）重復進行數據劃分：重復執行步驟2到4。為避免出現死循環，本實驗中將設定閾值為10以限制算法運行時間。算法結束條件設定為以下三個條件之一：

·聚類結果不再發生改變；

·K個中心點收斂（無變化）；

·執行了10次迭代。

（5）繪制聚類圖：對樣本數據經過聚類計算后，其聚類結果通過Python自帶的軟件庫繪制出聚類結果圖，圖1是K值為4時執行的兩次結果。

從聚類圖中可以看出，相同的K值，聚類結果有差異；經多次實驗，不同K值，其聚類效果不唯一。K值的選取是該算法的難點，K值設置太小則會導致相似度較小的數據發生聚類，使得結果過度模糊，中心內容不唯一，同時較小的K值會導致過多的更新聚類中心，進而致使運行時間也隨之增長；而當K值設置過大時則會導致聚類結果過度擬合，使得聚類簇數多而每個聚類簇內的數據量過少，從而導致多個聚類簇的中心內容相同，影響運行時間、效果。因此K個聚類中心不能明顯代表簇中心，導致運行時間加長，聚類效果變差，違背了聚類的本意。

（6）計算聚類效果準確性：本實驗中，實驗數據為688條，當K值為5時，第一次實驗結果準確性為64.4%，第二次實驗結果準確性為48.7%；當K值為4時，第一次實驗結果準確性為78%，第二次實驗結果準確性為66%。

2. 使用DBSCAN算法進行聚類

（1）計算相似度：使用TF-IDF以及余弦相似性來計算兩兩數據之間的相似度。此計算為前期準備過程，不參與DBSCSN的直接計算。

（2）確定領域范圍及領域范圍內數據的最小數量：依據數據之間的相似度來確定領域半徑，通過對相似度的觀察，可以看出其相似度主要集中在0、0.4、0.8附近，實驗中選取0.5作為領域半徑。領域半徑內數據的最小數量一般定的相對較小，本實驗中設定為5。

（3）實現領域半徑內數據聚類：隨機選取一個數據作為聚類中心，遍歷剩余數據，將與聚類中心的相似度大于領域半徑的數據分配給此聚類中心，同時將分配的數據標為已分配。

（4）遍歷所有數據：在未被標記的數據中重復執行步驟3，其結束條件為下列之一即可：·所有數據均被分配；

·未分配數據沒有在任一數據的領域范圍內；

·未分配數據少于領域范圍內最小數據量。

（5）繪制聚類圖：對樣本數據經過聚類計算后，其聚類結果通過Python自帶軟件庫繪制出聚類的結果圖，圖2是領域半徑為0.5、領域半徑數據最小數量為5時的實驗結果。

經過多次實驗，選取了具有明顯特征的聚類結果展示，在輸入參數相同的情況下，其聚類效果相同。該算法未直接保留數據之間的相似度，而是將其直接歸為簇中，使得數據間的聯系不能直觀顯示。該算法由于未直接確定聚類簇數，其聚類簇數不可直接預知且由領域半徑決定。從聚類結果中可以看出，領域半徑影響聚類結果，但對運行時間的影響微乎其微。領域半徑的取值依據先前的相似度來選取，提高了聚類效果的準確性，然而過大的領域半徑值仍然會使得聚類簇數增多，簇中的數據減少，甚至可能引起過度擬合，過小的領域半徑則相反。

（6）計算聚類效果準確性：本實驗中，實驗數據為688條，當領域半徑值為0.4、領域半徑內最小數據量為5時，實驗結果準確性為66%；當領域半徑值為0.5、領域半徑內最小數據量為5時，實驗結果準確性為86%。

3. 使用MajorClust算法進行聚類

（1）選取聚類中心：遍歷樣本數據，以數據預處理獲得的相似度為衡量標準，計算數據到其他所有數據的相似度并求其總和，將總和最大的數據設定為聚類中心，并將對聚類中心的相似度總和有絕對影響的數據與聚類中心進行聚類。未聚類的節點重復上述步驟，直至所有數據全部聚類完畢為止。此時的聚類結果是過度擬合的，由于每兩條或三條數據就形成一個聚類簇，因此選擇更新聚類中心來實現再一次聚類。

（2）更新聚類中心：在步驟1完成后會存在多個聚類簇，即每兩三個數據就會形成一個聚類簇，其聚類結果過度擬合，選取聚類簇中數據的最長子串作為新的聚類中心，原始數據依舊保存以便后期調取分析。

（3）重新聚類：對步驟2中重新選取的每個聚類簇的聚類中心兩兩計算相似度，形成最終聚類結果。

（4）繪制聚類圖：對樣本數據經過聚類計算后，兩兩相似度可直觀反映，因此通過軟件Gephi繪制出聚類的結果圖，如圖3所示。

由于該算法保留了數據間的相似程度，因此在聚類圖中可以直觀地看到數據內容、數據間相似度（數據間的相似度會顯示在數據間的連線上，由于聚類數據較多暫沒有顯示其相似度）。此聚類算法無需輸入聚類參數即可實現自動聚類，其結果客觀且準確度較高。在聚類過程中，相似度之和最大的數據的挑選會因數據量的增多而增加時間。在聚類結果中因其保留了數據記錄之間的相似度，使得后續分析更為直觀。

（5）計算聚類效果準確性：本實驗中，實驗數據為688條，實驗結果準確性為86%。

五、結果比較

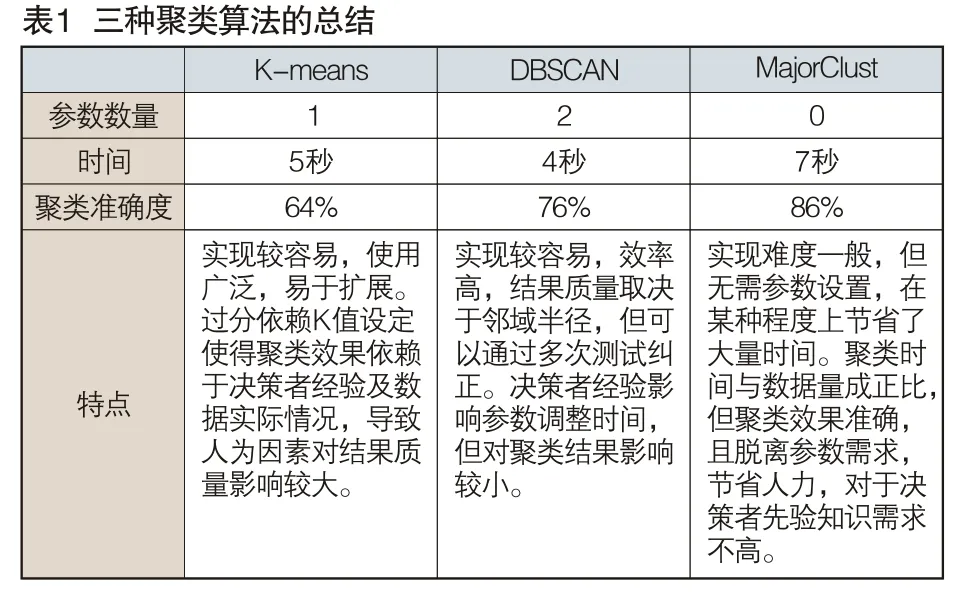
通過對auth.log日志文件的聚類，總結三種算法對此類型文件的適用情況，如表1所示。其中時間為實際實驗中聚類算法運行的平均時間，聚類準確性為實際聚類效果準確性的平均值。

?

在對auth.log日志文件的聚類中，使用了K-means、DBSCAN、MajorClust三種算法，由于算法本身存在自身特點，致使使用方式和效果不盡相同。在整個實驗中，使用的日志文件數據屬于文本類數據，且密度較稠密，DBSCAN算法和改進的MajorClust算法顯示出了良好的運行效果，而K-means算法則稍有遜色。三種算法首要區別是在參數的設置上，MajorClust算法不需要輸入任何參數即可自己實現聚類，而DBSCAN算法需輸入兩個參數、Kmeans需輸入一個參數，實驗中，參數的選擇相對較難，需要先驗經驗和不斷嘗試，這要求取證人員具備較高的技術水平和豐富的實踐經驗，因為參數的選擇直接影響聚類效果的優劣，若能基于先驗經驗給出精確的參數，那么其參數問題便可忽略。算法的運行時間在一定程度上反映著算法的運行效率，這在電子數據取證過程中至關重要，因為通常服務器日志較實驗日志極大，分析極為耗時。本實驗中相似度的計算是每個算法必有的運行時間，K-means算法運行時間主要依賴于K個聚類中心的不斷更新，而聚類中心的更新則取決于數據的稠密程度；DBSCAN算法只要設定好領域半徑即可快速運行；改進的MajorClust算法依賴相似度的總和，因此其運行時間取決于數據集的數量。實驗運行結果顯示出三種算法各自的特征，就文本數據集而言，在偵破服務器入侵類犯罪時，K-means算法更適合于數據內容有明顯差異的數據集，DBSCAN算法對稠密的數據有良好的運行能力，適合短時間內分析海量日志內容，節省案件偵破周期，而Majorclust算法適應范圍較廣，效果突出，但耗時略長，在時間充裕的情況下能準確鎖定關鍵信息，協助偵查人員縮小偵查范圍，指明偵查方向。綜上所述，在服務器入侵類案件針對日志進行電子數據取證的過程中，根據具體情況結合不同的聚類算法分析日志方能在最短時間內準確定位關鍵信息。