剪叉式高空車轉向機構結構分析

陸進添， 劉丹， 鄧安田

（三一帕爾菲格特種車輛裝備有限公司研究院，江蘇南通226000）

0 引 言

轉向機構是高空作業車轉向系統的主要執行組件，為適應高空車在狹小的空間移動轉向等工況，需要轉向機構能夠使作業車有較小的轉彎半徑，同時盡可能減輕或避免磨胎，對轉向機構的研究有利于增強高空車的轉向性能、改善磨胎、減小轉向力和增強操作穩定性。

1 轉向機構簡介

單油缸式的轉向機構如圖1所示，具有良好的轉向性能，能夠適應高空作業車的轉向要求。對轉向油缸的進出油口進行控制，驅動活塞桿運動，活塞桿的運動帶動轉向連桿，轉向連桿作用于連桿軸，使轉向輪克服地面的摩擦阻力矩，連同轉向支架一起繞轉向軸轉動，從而達到轉向目的。

2 轉向機構分析

2.1 轉向機構各構件的位置分析

確定轉向輪的位置可以分析轉向系統的轉向性能和轉向特性，確定轉向連桿的位置是進行轉向機構受力的必備前提，因此在受力分析之前需要進行轉向機構的位置分析。轉向機構的位置參數如圖2所示，長度參數的含義如表1所示，角度參數在引用時指明含義。

表1 某系列的轉向機構設計參數

對于從車尾向車頭看右轉 向 輪（ 圖2 左邊），連桿與活塞桿鉸接的位置 為 變量，則其位置為（x,-a）。由余弦定理可得連桿與搖桿的夾角（傳動角）α為

輔助角Ω為

液壓缸桿右端轉動副位置與y方向的夾角ψ為

ψ=arctan（x/a）。

初始位置搖桿與x負方向的夾角φ為

φ=arctan（c/d）。

車輪轉角ω（向外側為正）為

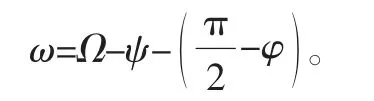
則連桿與x軸方向的夾角為

β=（ω-φ）+α。

同理，對于左側車輪連桿與活塞桿鉸接的位置為變量x，則左側的位置為（x′,-a）。

且有

x′=x+s。

由余弦定理可得連桿與搖桿的夾角（傳動角）為

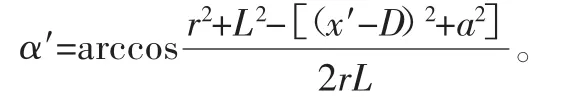
輔助角Ω′為

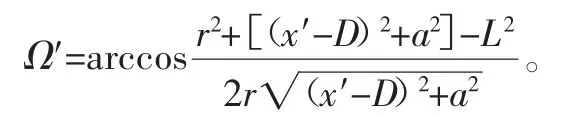
液壓缸桿右端轉動副位置與x負方向的夾角ψ′為

ψ′=arctan[a/（D-x′）]。

初始位置搖桿與x方向的夾角φ′為

φ′=arctan（c/d）。

車輪轉角ω′（向外側為正）為

ω′=π-φ′-Ω′-ψ′。

則連桿與x軸方向的夾角為

β′=α′-ω′-φ′。

即得到兩側車輪轉角對活塞桿伸出量的變化關系：

其中活塞桿的伸出量為

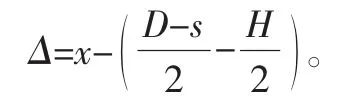
2.2 原地轉向阻力矩的計算

車輛的轉向阻力矩是由于地面和轉向輪之間的相互作用及轉向系統內部摩擦共同作用產生的[1]，車輪靜態下的轉向阻力矩是最大的轉向阻力矩[2]。轉向系統的轉向力主要用于克服轉向阻力矩以實現轉向，因此若要確定液壓油缸的轉向壓力，首先應確定車輪與地面之間的最大原地轉向阻力矩。

由作業車的各種工況可計算出轉向輪單輪最大輪載FN。

實心輪胎的寬度為D，下沉量與輪載關系如表2所示，表2數據的線性擬合為：

y=245x+535；

R2=0.98。

表2 載荷與下沉量關系

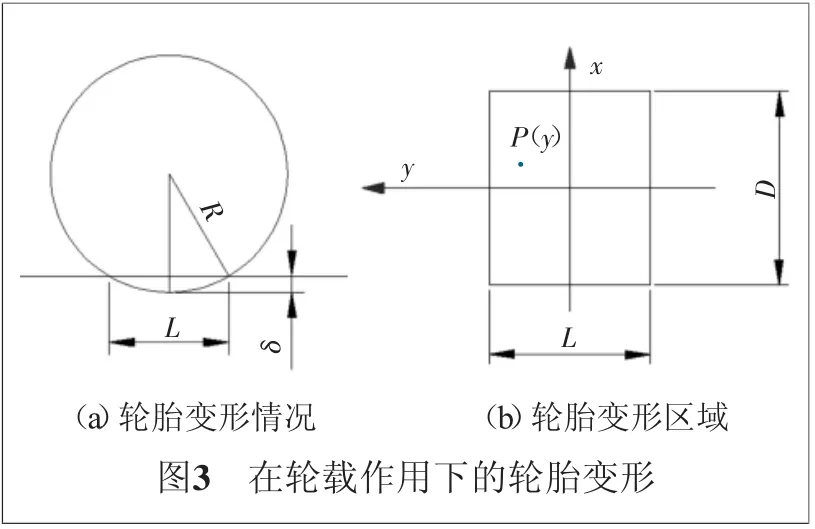
由此可得輪載FN對應的變形量為δ，對應輪胎的變形情況和變形區域如圖3所示，接觸區域近似成矩形，根據幾何關系可得輪胎與地面接觸區域長度為

假設輪胎變形區域的壓強從中部向兩邊線性遞減，接觸區域的壓強可表示為：

接觸區的壓力是接觸區壓強的綜合作用效果，則

可得Pmax=2FN/（DL）。

于是接觸區域的壓強為：

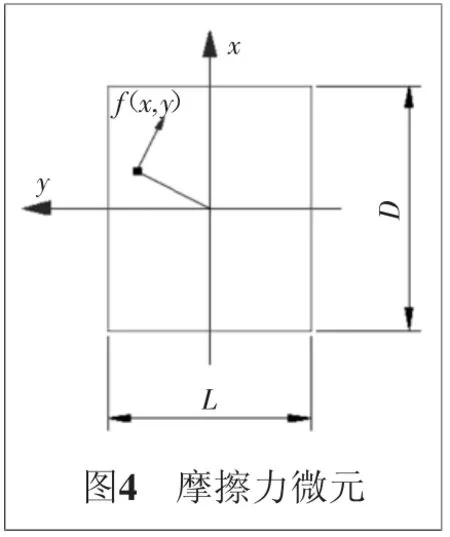
選取摩擦力微元，如圖4所示，在一點Q(x,y)處的摩擦力微元為

df（x,y）=μ（x,y）P（x,y）dS=μ（x,y）P（x,y）dxdy。

其中，滑動摩擦因數μ（x,y）=μ=0.7。

此微元所對應的阻力矩為

dM（x,y）=rdf（x,y）。

于是，在整個接觸區域Ω的原地轉向阻力矩為

即為

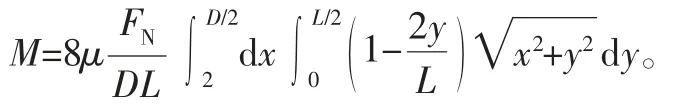
代入相關數值直接在Mathematic軟件中進行求解，即可得到數值解，以及兩種假設下轉向阻力矩的差異。

2.3 轉向機構受力分析

原地轉向阻力矩是轉向機構阻力的主要來源，轉向機構的受力分析圖如圖5所示，其中：L表示連桿、Y表示搖桿、H表示活塞桿、J表示機架、F表示力、1表示右側轉向、2表示左側轉向。

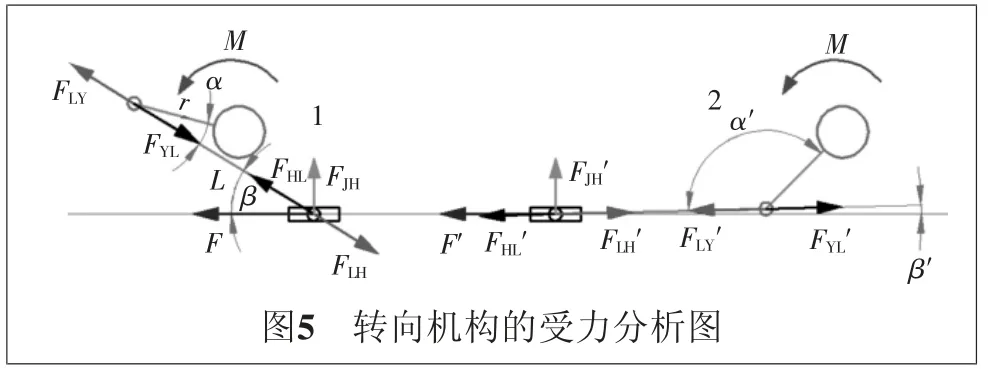
對搖桿由力矩平衡得：

M-rFLYsinα=0；M-r′FLY′sinα′=0。

由于連桿是二力桿，結合牛頓第三定律則，有：

FLY=FYL=FHL=FLH；FLY′=FYL′=FHL′=FLH′。

對活塞桿受力平衡有：

FHLcosβ-F=0；FJH+FLHsinβ=0；

FHL′cosβ-F′=0；FJH′+FLH′sinβ=0。

轉向機構的各個部件的受力情況如表3所示。

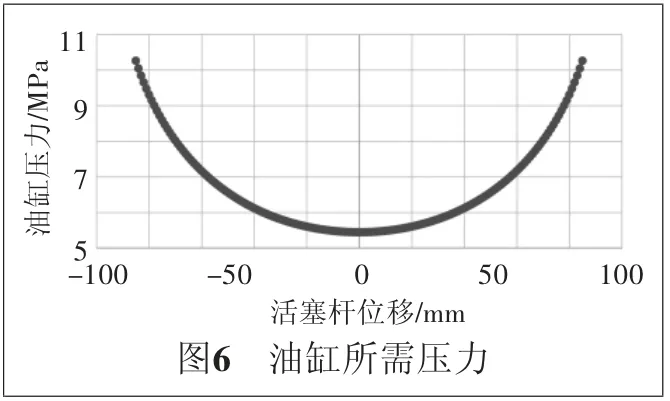
由此可確定油缸壓力為

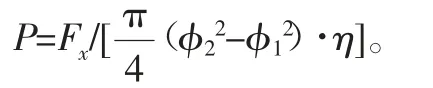
所對應的壓力曲線如圖6所示，可確定油缸的最大壓力。

表3 部件受力結果

3結論

根據設計需要，本文采用解析法對轉向機構的組成部件的位置和受力進行理論推導，確定了各組成部件的位置變化關系及傳動角的性能參數。根據實心靜音輪胎的承載曲線，結合輪胎與地面的接觸形狀，通過元素法確定了高空作業車的原地轉向阻力矩的計算方法，基于原地轉向阻力矩的計算得到了油缸壓力隨活塞桿伸縮量的變化關系，確定了液壓油缸所需最大壓力。研究結果對剪叉式高空作業車轉向系統的設計提供了依據。