軟態TP2銅材室溫抗拉強度的概率分布

張紅衛， 楊帆， 劉岑， 劉兵， 范有雄， 劉小寧

（1. 武漢軟件工程職業學院，武漢430205；2. 湖北輕工職業技術學院，武漢430070）

0 引 言

在食品、醫藥、衛生、醫療領域及人們日常生活中，往往采用軟態TP2銅管輸送的氣體或者液體介質有一定工作壓力的，為確保安全，工程上采用有關標準[1-2]規范軟態TP2銅管的強度設計。

對于鋼制壓力容器或其他鋼制結構，其制造材料抗拉強度與幾何尺寸等受到制造加工等因素的影響[3]，具有隨機不確定性，工程界與學術界對鋼制壓力容器或其他鋼制結構強度的可靠性設計方法進行了探索[4-7]。目前，對TP2銅管強度可靠性設計方法的研究還不充分[8-9]，有待加強；由于軟態TP2銅材抗拉強度概率分布是建立銅管強度可靠性設計方法的基礎工作，因此，軟態TP2銅材抗拉強度的概率分布是工程界與學術界值得研究的課題。

軟態TP2銅材抗拉強度的概率分布包括分布規律與分布參數兩個方面，文中基于24組軟態TP2銅管室溫實測爆破壓力[9]，應用數理統計理論與方法[10-11]，研究了軟態TP2銅材室溫抗拉強度的概率分布。

1 建立方法

1.1 銅材抗拉強度與銅管爆破壓力

研究表明，若不考慮銅管端部對銅管爆破壓力的加強作用，TP2銅光管與銅內螺紋管的爆破壓力可用中徑公式計算[9]，若通過試驗獲得銅管實測爆破壓力，則軟態TP2銅材的抗拉強度為

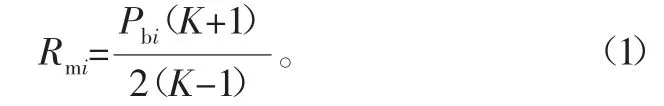
式中：Pbi為軟態TP2銅管的第i個實測爆破壓力的有效值，MPa；Rmi為軟態TP2銅材抗拉強度的第i個實測值，MPa；K為銅管的徑比。

1.2 銅材抗拉強度的平均值與精密度

對n組抗拉強度實測值進行統計，可得到其平均值與精密度：

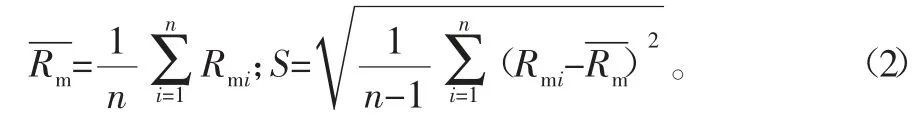
1.3 銅材抗拉強度實測值的同質性判別

在相同條件時，如果抗拉強度實測值來源于不同測試單位，必須考慮這些數據是否存在系統誤差，即對這些數據必須進行同質性判別。

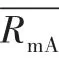
假設RmA與RmB基本符合正態分布，則RmA的分布參數分別為均值μA與標準差σA，RmB的分布參數分別為均值μB與標準差σB；RmA與RmB具有同質性的條件為其均值與標準差分別無顯著差異。

1.3.1 標準差無顯著差異的判別

根據數理統計知識，t分布是檢驗兩個標準差σA與σB是否存在差異的有效工具[14-20]，檢驗依據為

當檢驗依據F滿足判據

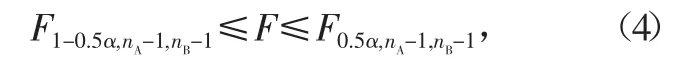
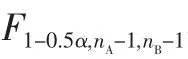
取判別兩個標準差無顯著差異的顯著度α=0.01，文中所用的F分布系數如表1所示。

1.3.2 均值無顯著差異的判別

根據數理統計知識，t分布是檢驗兩個均值μA與μB是否存在差異的有效工具。假設σA=σB，均值μA與μB的比較依據為

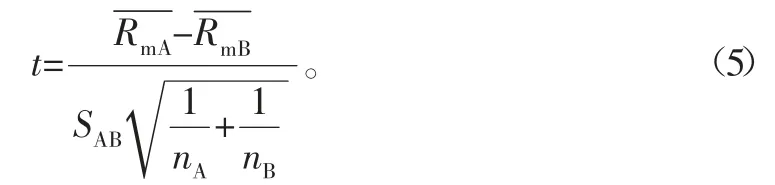
當t滿足判據

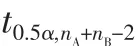
取判別兩個均值無顯著差異的顯著度α=0.01，文中所用的t分布系數如表1所示。

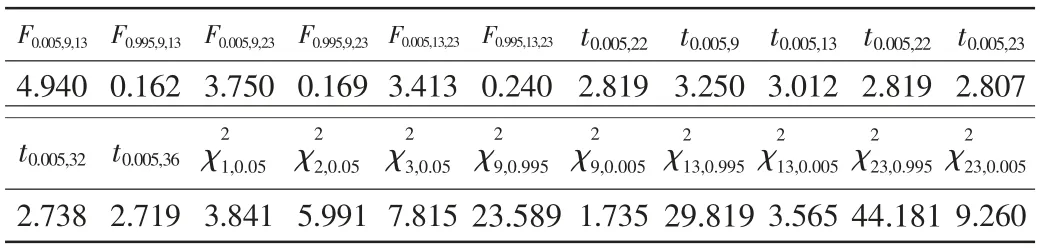
表1 有關系數

1.3.3 無顯著差異的評價

只有當式（4）與式（6）同時滿足時，才能說明在A與B單位測量得到的數據無系統誤差，即RmA與RmB具有同質性，可以將兩個單位測得的數據合并作為抗拉強度實測值統計的基本數據。

1.4 分布規律的假設檢驗

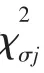
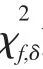
1.5 分布參數及取值范圍

當軟態TP2銅材抗拉強度基本符合正態分布時，其分布參數包括均值μ、標準差σ與變異系數C。雙側置信度為（1-α）時，可通過有限的試驗數據分析分布參數的取值范圍。

1.5.1 均值的取值范圍

均值μ的取值范圍為

其中：

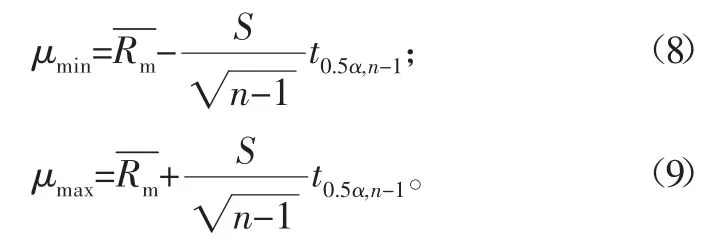
式中：μmin與μmax分別為抗拉強度Rm均值μ的下限與上限；t0.5α,n－1為t分布系數。

本文取α=0.01，即在雙側置信度為99%時，分析均值的取值范圍，所用的t分布系數如表1所示。

1.5.2 標準差的取值范圍

標準差σ取值范圍為

其中：

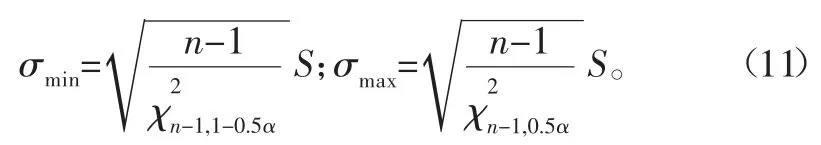
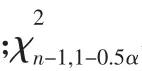
取α=0.01，即雙側置信度為99%時，分析標準差的取值區間，所用的χ2分布系數如表1所示。

1.5.3 變異系數的取值范圍

變異系數C 取值范圍為

其中：

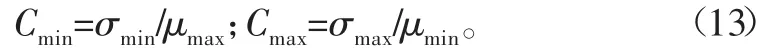
式中，Cmin與Cmax分別為C 的下限與上限。

2 實測抗拉強度

對軟態TP2銅光管與銅內螺紋管進行室溫液壓爆破試驗，有關企業獲得了10組爆破壓力的有效試驗數據，筆者也獲得14組爆破壓力的有效試驗數據，現將有效試驗數據分別列入表2。

研究表明，在相同條件時，銅光管與銅內螺紋管的爆破壓力無明顯差異。為了分析企業提供的有效試驗數據與本文測量得到有效數據是否存在明顯差異，將企業提供的10組有效試驗數據與本文測量得到14組有效數據進行統計，統計值也列入表2中。

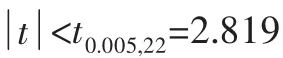
由于F與t同時滿足式（4）與式（6），因此，企業提供的有效試驗數據與本文測量得到有效數據具有同質性，可將其有效試驗數據合并計算，得到抗拉強度的實測值Rmi及其平均值與標準差，一并列入表2中。

3 分布規律

3.1 基于文獻［9］提供的數據（A）

基于文獻［9］提供的10組數據（表2序號1～10），假設軟態TP2銅材的室溫抗拉強度Rm基本符合正態分布。因1+3.3lg10=4.30，可將10組同質性統計數據分為5個區間，由自由度為f= 5-1-2=2與顯著度δ=0.05查表1，可得皮爾遜的臨界值為5.991。表3上半部分是每個區間統計量實際頻數Nj與理論頻數n×pj差異的皮爾遜統計量及其之和。

表3上半部分表明皮爾遜統計量之和為7.4348，大于臨界值5.991，似不能通過檢驗；但是，造成這種情況的原因可能是數據比較少且分組不合理［16］；考察表3上半部分，發現第4與第5組數據的實際頻數與理論頻數差異的皮爾遜統計量差異大，若將第4與第5組數據合并，其皮爾遜統計量及其之和可大幅度減少。

因此，將表3上半部分第4與第5組合并為1個區間后，重新進行統計計算。表3下半部分是合并后實際頻數Nj與理論頻數n×pj差異的皮爾遜統計量及其之和。因合并后的自由度為f=4-1-2=1，取顯著度δ=0.05，由表1得皮爾遜統計量之和的臨界值為3.841。由表3下半部分可知：參考文獻[9]提供數據的皮爾遜統計量之和為1.3125，小于臨界值3.841，表明顯著度為0.05時，室溫抗拉強度Rm基本符合正態分布。

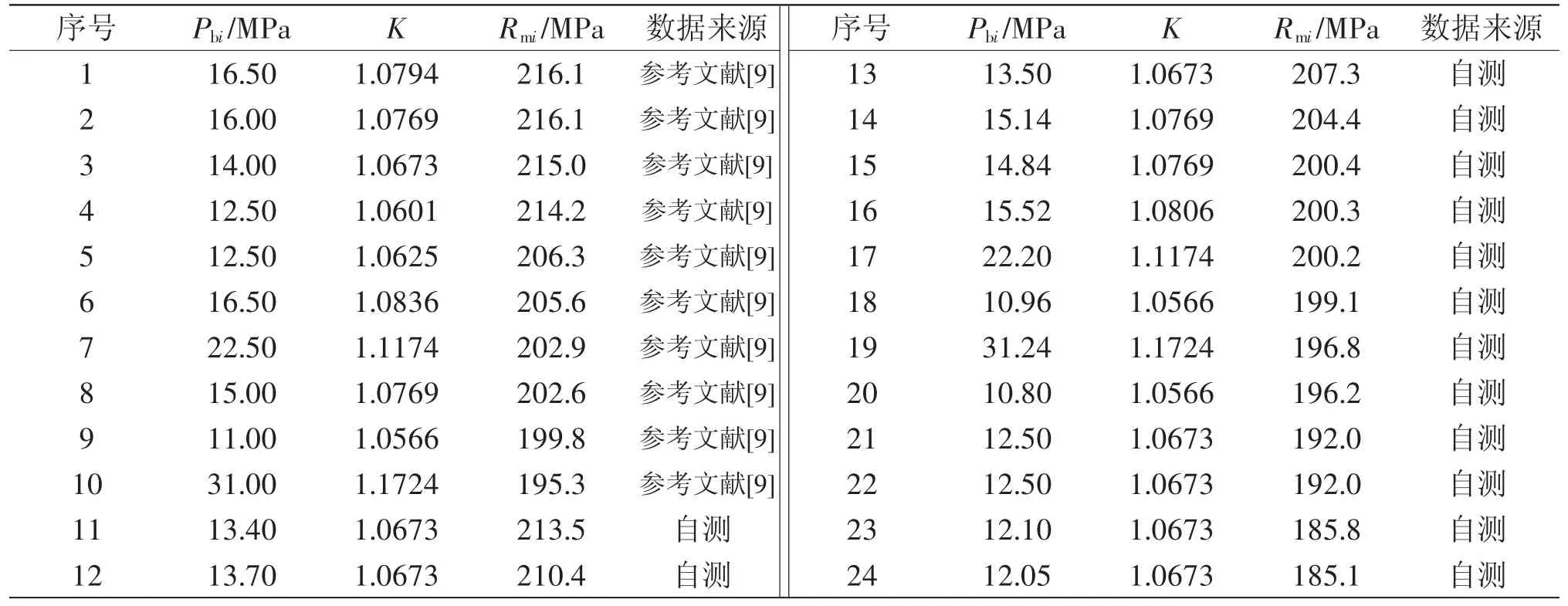
表2 室溫抗拉強度的實測值與統計

表3 參考文獻［9］提供數據的皮爾遜統計量

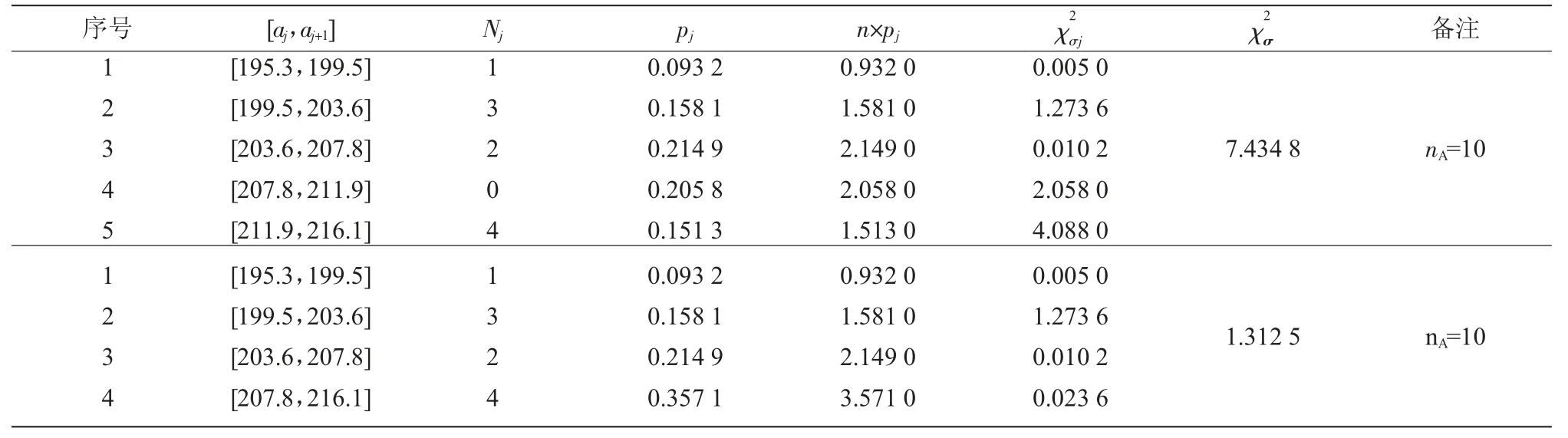
表3 參考文獻［9］提供數據的皮爾遜統計量

序號[aj，aj+1]Njpjn×pjχ2 σjχ2σ備注12345[195.3，199.5][199.5，203.6][203.6，207.8][207.8，211.9][211.9，216.1]13204 0.093 2 0.158 1 0.214 9 0.205 8 0.151 3 0.932 0 1.581 0 2.149 0 2.058 0 1.513 0 0.005 0 1.273 6 0.010 2 2.058 0 4.088 0 7.434 8nA=10 1234[195.3，199.5][199.5，203.6][203.6，207.8][207.8，216.1]1324 0.093 2 0.158 1 0.214 9 0.357 1 0.932 0 1.581 0 2.149 0 3.571 0 0.005 0 1.273 6 0.010 2 0.023 6 1.312 5nA=10

3.2 基于自測數據（B）

基于文中自測的14組數據（表2序號11～24），假設軟態TP2銅材的室溫抗拉強度Rm基本符合正態分布。因1+3.3lg14 =4.78，可將14組同質性統計數據分為5個區間，由自由度為f=5-1-2=2與顯著度δ=0.05查表1，可得皮爾遜統計量的臨界值為5.991。每個區間實際頻數Nj與理論頻數n×pj差異的皮爾遜統計量及其之和如表4所示。

根據表4，自測數據的皮爾遜統計量之和為1.096 8，小于臨界值5.991，表明顯著度為0.05時，室溫抗拉強度Rm是基本符合正態分布的隨機變量。

表4 自測數據皮爾遜統計量

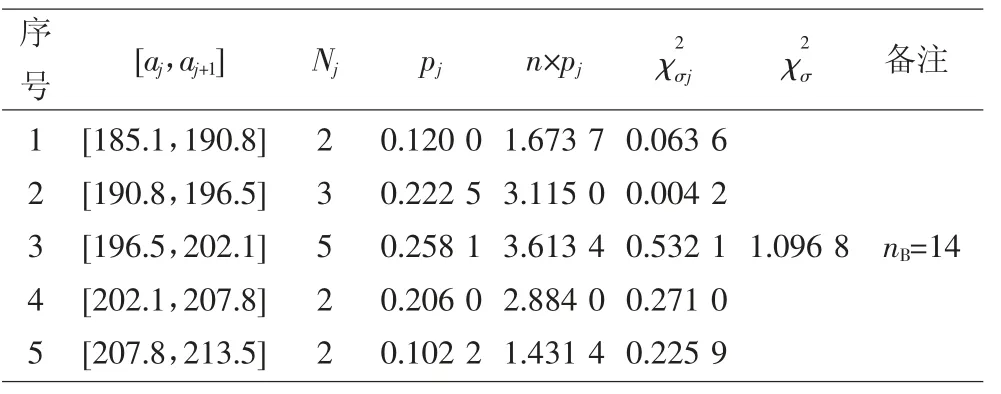
表4 自測數據皮爾遜統計量

序號[aj，aj+1]Njpjn×pjχ2 σjχ2 σ備注12345[185.1，190.8][190.8，196.5][196.5，202.1][202.1，207.8][207.8，213.5]23522 0.120 0 0.222 5 0.258 1 0.206 0 0.102 2 1.673 7 3.115 0 3.613 4 2.884 0 1.431 4 0.063 6 0.004 2 0.532 1 0.271 0 0.225 9 1.096 8 nB=14

3.3 基于全部試驗數據（D）

基于全部24組試驗數據（表2序號1～24），假設軟態TP2銅材的室溫抗拉強度Rm是基本符合正態分布的隨機變量。因1+3.3lg24 =5.55，可將24組同質性試驗數據分為6個區間，根據自由度f=6-1-2=3與顯著度δ=0.05查表1，可得皮爾遜統計量的臨界值為7.815。每個區間實際頻數與理論頻數差異的皮爾遜統計量及其之和為4.103 2（如表5），小于臨界值7.815，因此在顯著度為0.05時，室溫抗拉強度Rm基本符合正態分布。

表5 基于24組試驗數據的皮爾遜統計量

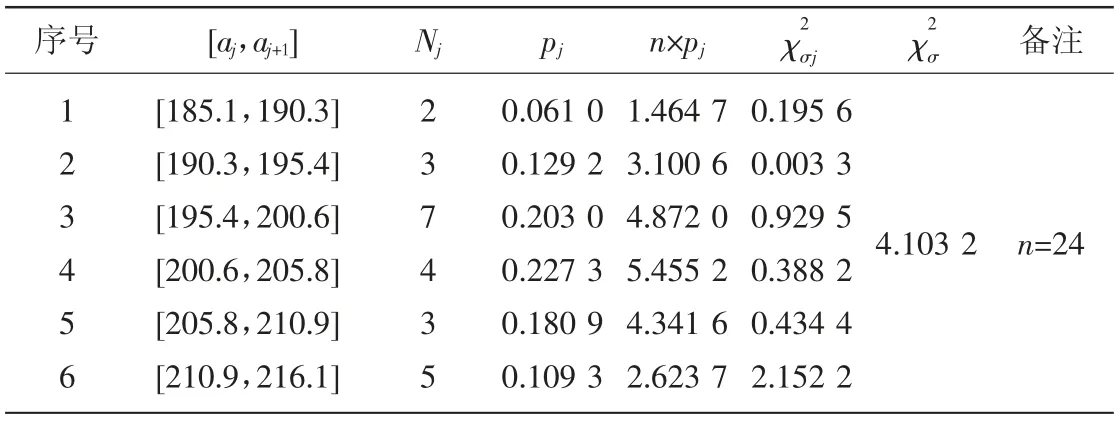
表5 基于24組試驗數據的皮爾遜統計量

序號[aj，aj+1]Njpjn×pjχ2 σjχ2 σ備注123456[185.1，190.3][190.3，195.4][195.4，200.6][200.6，205.8][205.8，210.9][210.9，216.1]237435 0.061 0 0.129 2 0.203 0 0.227 3 0.180 9 0.109 3 1.464 7 3.100 6 4.872 0 5.455 2 4.341 6 2.623 7 0.195 6 0.003 3 0.929 5 0.388 2 0.434 4 2.152 2 4.103 2 n=24

4 分布參數

雙側置信度為99%時，根據表2提供的軟態TP2銅材室溫抗拉強度試驗數據，分析分布參數取值范圍。

4.1 基于文獻［9］提供的數據（A）

將表2序號1～10的10組同質性試驗數據的平均值與精密度代入式（7）～式（13），分別得室溫抗拉強度Rm分布參數均值μA、標準差σA與變異系數CA取值范圍：

4.2 基于自測數據（B）

將表2序號11～24的14組同質性試驗數據的平均值與精密度代入式（7）～式（13），分別得室溫抗拉強度Rm分布參數均值μB、標準差σB與變異系數CB取值范圍：

4.3 基于全部試驗數據（D）

將表2中24組同質性試驗數據的平均值與精密度代入式（7）～式（13），分別得室溫抗拉強度Rm的分布參數均值μD、標準差σD與變異系數CD取值范圍：

顯然，用24組同質性試驗數據的平均值與精密度，確定軟態TP2銅材室溫抗拉強度Rm的分布參數及其取值范圍相對合理。

5 討 論

根據以上分析，基于文獻[9]提供的數據（A）、自測數據（B）及文中全部試驗數據（D），室溫軟態TP2銅材的抗拉強度Rm基本符合正態分布，其中由文獻[9]提供的數據與自測數據的統計分析，可知室溫抗拉強度Rm的分布參數無明顯差異，即軟態TP2銅材的室溫抗拉強度Rm在A與B時，基本是同一個隨機變量；將文中全部試驗數據稱為D（D為A與B的合并），討論室溫抗拉強度Rm的分布參數在D與A和B時的關系。

5.1 標準差比較

1）試驗數據D與試驗數據A。由式（3）可得比較統計值F=0.698，查表1得F0.005,9,23=3.750 與F0.995,9,23=0.169，F滿足式（4），即0.169≤F≤3.750；因此，顯著度為0.01時，D與A的兩個標準差無顯著差異。

2）試驗數據D與試驗數據B。由式（3）得比較統計值F=0.878，查表1得F0.005,13,23=3.413與F0.995,13,23=0.240，F滿足式（4），即0.240≤F≤3.413；因此，顯著度α為0.01時，D與B的兩個標準差無顯著差異。

5.2 均值比較

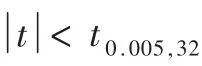
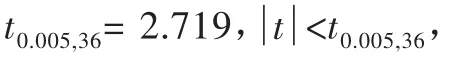
5.3 評 價

由于D與A 、D與B和A與B的F分布系數與t分布系數分別同時滿足式（4）與式（6），因此，基于A、B與D的試驗數據，室溫軟態TP2銅材的抗拉強度Rm是同一個基本符合正態分布的隨機變量。

5.4 分布參數的優化

由以上分析可知，室溫軟態TP2銅材的抗拉強度是同一個基本符合正態分布的隨機變量，其主要分布參數均值μ的取值范圍應是μA、μB與μD的公共部分，標準差σ的取值范圍應也是σA、σB與σD的公共部分，即

其中：

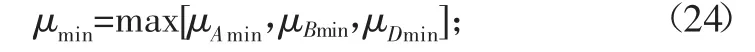
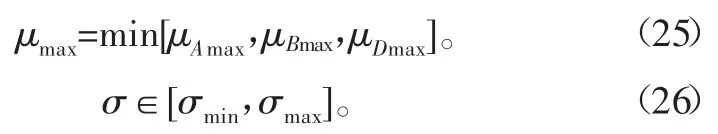
其中：

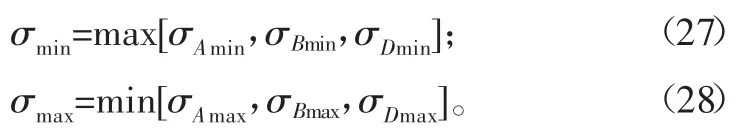
將式（14）與式（15）、式（17）與式（18）及式（20）與式（21）代入到式（23）～式（28），可得到優化后主要分布參數均值μ、標準差σ與變異系數C的取值范圍：

比較式（29）與式（20）、式（31）與式（22）可知，優化后軟態TP2銅材的室溫抗拉強度的均值與標準差波動范圍變小，精度得到提高。

6 結 語

基于24組軟態TP2銅管的實測爆破壓力，應用數理統計理論與方法，分析了室溫軟態TP2銅材抗拉強度的分布規律與參數，得到如下結論：1）顯著度為0.05時，室溫軟態TP2銅材抗拉強度是基本符合正態分布的隨機變量；2）雙側置信度為99%時，室溫軟態TP2銅材抗拉強度的均值不小于199.3 MPa且不大于205.8 MPa，標準差不小于6.483 MPa且不大于14.16 MPa，變異系數位于0.031 50與0.071 05之間。