基于高斯消元的BATS碼的改進(jìn)譯碼算法*

楊 娟，嵇建波，李海兵

（桂林航天工業(yè)學(xué)院，廣西 桂林 541004）

0 引 言

近年來(lái)，無(wú)線通信在世界范圍內(nèi)迅速發(fā)展，并且諸如移動(dòng)TV、推送型信息等無(wú)線服務(wù)已廣泛應(yīng)用于實(shí)際生活。其中，多播和廣播是此類應(yīng)用中的常見操作，引起了研究者的極大興趣。然而，由于無(wú)線信道衰落和信號(hào)干擾，多播網(wǎng)絡(luò)的數(shù)據(jù)傳輸變得不可靠。為了提高網(wǎng)絡(luò)的可靠性，楊偉豪和張珍提出網(wǎng)絡(luò)編碼（Network Coding，NC）的思想，即允許中間節(jié)點(diǎn)對(duì)輸入數(shù)據(jù)包進(jìn)行編碼。網(wǎng)絡(luò)編碼在增強(qiáng)無(wú)線網(wǎng)絡(luò)可靠性的同時(shí)，實(shí)現(xiàn)了更高的網(wǎng)絡(luò)吞吐量。然而，網(wǎng)絡(luò)編碼在提升可靠性和吞吐量等性能的同時(shí)，也面臨著系數(shù)開銷大、長(zhǎng)延遲等問題，使其無(wú)法廣泛應(yīng)用于實(shí)際生活。

為了平衡編碼開銷/譯碼復(fù)雜度和吞吐量問題，Shenghao Yang等人于2011年提出了批量稀疏碼（Batched Sparse Codes，BATS Codes）[1-2]的概念。BATS碼是一種將噴泉碼[3-5]和網(wǎng)絡(luò)編碼相結(jié)合的一種新型編譯碼方案，在發(fā)送端將要傳送的數(shù)據(jù)信息分成特定長(zhǎng)度的源數(shù)據(jù)包，根據(jù)度分布函數(shù)選出源數(shù)據(jù)包并對(duì)其進(jìn)行外碼編碼，生成以批次為單位的編碼包在信道上進(jìn)行傳輸。在中繼節(jié)點(diǎn)，對(duì)接收到的批次進(jìn)行批次內(nèi)的隨機(jī)線性網(wǎng)絡(luò)編碼后傳輸?shù)浇邮斩恕＝?jīng)過信道傳輸后，接收端不需要考慮信道條件，只要保證接收到足夠數(shù)量的批次，就一定可以成功譯碼，從而恢復(fù)要傳送的源數(shù)據(jù)信息。BATS碼作為一種較新穎的信道編碼技術(shù)，繼承了噴泉碼和網(wǎng)絡(luò)編碼的優(yōu)點(diǎn)。憑借其無(wú)碼率特性和無(wú)需反饋、中斷可續(xù)傳、吞吐量高、安全性高、復(fù)雜度低等優(yōu)點(diǎn)，近些年成為通信領(lǐng)域研究的熱點(diǎn)[6]。

BATS碼在BP譯碼方式下的漸進(jìn)譯碼性能分析已經(jīng)在文獻(xiàn)[7-8]中描述過，當(dāng)原始數(shù)據(jù)包趨近無(wú)限長(zhǎng)時(shí)，BP譯碼器可以以較高概率恢復(fù)固定比例（接近1）的原始輸入包，但是當(dāng)原始數(shù)據(jù)包數(shù)量有限時(shí)，譯碼性能將會(huì)有較大幅度衰減[9-10]。因此，在接收端計(jì)算資源充足的情況下，可以考慮在BP譯碼后級(jí)聯(lián)高斯消元譯碼算法[11]。采用高斯消元算法，當(dāng)矩陣滿秩時(shí)可將輸入數(shù)據(jù)包譯出，但如果矩陣不滿足滿秩的條件，系數(shù)矩陣對(duì)應(yīng)的輸入數(shù)據(jù)包則完全譯不出。推薦的算法利用當(dāng)系數(shù)矩陣不滿秩時(shí)也存在部分可譯包的事實(shí)，識(shí)別并判斷這些可譯包并將其譯出，從而提高高斯消元的譯碼性能。

1 BATS碼的編譯碼原理

編碼BATS碼在大小為q的有限域F中，對(duì)K個(gè)原始數(shù)據(jù)包進(jìn)行編碼，每個(gè)數(shù)據(jù)包有T個(gè)符號(hào)。每個(gè)包可表示為FT中的一個(gè)列向量，因此可以將K個(gè)輸入的原始數(shù)據(jù)包用矩陣表示：

其中bi是第i個(gè)包，因此B也可以看作是輸入數(shù)據(jù)包的集合。

在發(fā)送端，首先對(duì)度分布進(jìn)行采樣，得到一個(gè)整數(shù)di。在B中隨機(jī)選擇di個(gè)輸入包構(gòu)成Bi。將這di個(gè)包進(jìn)行隨機(jī)線性組合得到一個(gè)批次，每個(gè)批次包括M個(gè)編碼包。這個(gè)過程可用下述矩陣方程進(jìn)行表示：

按順序依次生成各個(gè)批次，并由發(fā)送端發(fā)送至中間節(jié)點(diǎn)。在中間節(jié)點(diǎn)，采用隨機(jī)網(wǎng)絡(luò)線性編碼對(duì)每一個(gè)批次進(jìn)行批次內(nèi)部再編碼。網(wǎng)絡(luò)中，假設(shè)每個(gè)批次的端到端傳輸是線性操作，給定一個(gè)目的節(jié)點(diǎn)，Hi是第i個(gè)批次的轉(zhuǎn)移矩陣，Yi是其對(duì)應(yīng)批次的輸出數(shù)據(jù)包，可以得到：

轉(zhuǎn)移矩陣Hi與內(nèi)碼編碼和網(wǎng)絡(luò)的拓?fù)浣Y(jié)構(gòu)有關(guān)，不同的批次對(duì)應(yīng)的Hi可以不同。假設(shè)Hi在接收端是已知的。事實(shí)上，在線性網(wǎng)絡(luò)編碼中，在目的節(jié)點(diǎn)確實(shí)可以通過存放于包頭的系數(shù)向量獲得轉(zhuǎn)移矩陣的信息。

上述外碼和內(nèi)碼的編碼方法可以用唐納圖描述，如圖1所示，有K個(gè)變量節(jié)點(diǎn)。變量節(jié)點(diǎn)用實(shí)心圓表示，其中變量節(jié)點(diǎn)i對(duì)應(yīng)第i個(gè)原始數(shù)據(jù)包bi；方塊表示校驗(yàn)節(jié)點(diǎn)也就是批次碼，其中校驗(yàn)節(jié)點(diǎn)j對(duì)應(yīng)第j個(gè)批次Yj。如果bi參與了Yj的生成，則說(shuō)明校驗(yàn)節(jié)點(diǎn)j與變量節(jié)點(diǎn)i相連。與每個(gè)校驗(yàn)節(jié)點(diǎn)j相關(guān)的是生成矩陣Gj，Hj表示轉(zhuǎn)移矩陣。

圖1 BATS codes的唐納圖

在接收端，首先由BP譯碼器對(duì)接收到的批次碼進(jìn)行譯碼。由式（3）可知，目的節(jié)點(diǎn)可以通過Yi、Gi和Hi的信息進(jìn)行譯碼得到Bi，其中i=1,2,…,n。譯碼過程等價(jià)于求解式（3）對(duì)應(yīng)的線性系統(tǒng)方程組。BP譯碼過程可以由圖2進(jìn)行直觀描述，第一行是變量節(jié)點(diǎn)代表輸入數(shù)據(jù)包，第二行是校驗(yàn)節(jié)點(diǎn)表示接收到的各個(gè)批次碼，整體轉(zhuǎn)移矩陣GiHi與校驗(yàn)節(jié)點(diǎn)i相關(guān)聯(lián)。

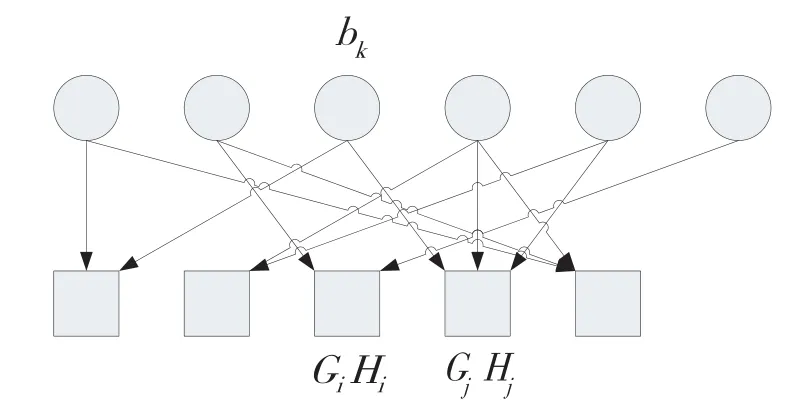
圖2 譯碼圖

當(dāng)?shù)趇個(gè)校驗(yàn)節(jié)點(diǎn)的秩rk(GiHi)等于它的度di時(shí)，校驗(yàn)節(jié)點(diǎn)i是可譯的。因此，Bi可以通過解方程Yi=BiGiHi恢復(fù)，且得到的是唯一解。當(dāng)恢復(fù)出Bi中的di個(gè)原始數(shù)據(jù)包后，將這些恢復(fù)出的原始包替換到還未譯碼的批次中。假設(shè)bk在Bi中，如果只有一條邊與變量節(jié)點(diǎn)k相連，邊的另一個(gè)頂點(diǎn)是校驗(yàn)節(jié)點(diǎn)i，此時(shí)直接移除變量節(jié)點(diǎn)k，它不再參與后續(xù)譯碼過程；如果變量節(jié)點(diǎn)k還與校驗(yàn)節(jié)點(diǎn)j相連且j≠i，通過替換過程，校驗(yàn)節(jié)點(diǎn)j的度數(shù)降1，并刪除Gj中對(duì)應(yīng)于變量節(jié)點(diǎn)k的那一行。在譯碼圖中，這個(gè)過程相當(dāng)于首先刪除校驗(yàn)節(jié)點(diǎn)i以及與之相連的變量節(jié)點(diǎn)，然后更新與該變量節(jié)點(diǎn)相連的其他校驗(yàn)節(jié)點(diǎn)的信息，重復(fù)這些步驟直至沒有可解的校驗(yàn)節(jié)點(diǎn)，最終譯碼得到原始輸入數(shù)據(jù)包。

圖3 當(dāng)矩陣滿秩時(shí)的高斯消元過程

當(dāng)BP譯碼算法停止后，可以將剩下的未譯出的批次碼的系數(shù)矩陣合并成一個(gè)系數(shù)矩陣。如果合并后的系數(shù)矩陣是滿秩的，對(duì)其采用高斯消元算法可以將剩下的輸入數(shù)據(jù)包譯出，否則如果系數(shù)矩陣不滿秩，則高斯消元算法無(wú)解，譯碼過程停止。考慮一個(gè)線性系統(tǒng)Y=AX，傳統(tǒng)的高斯消元算法的步驟包括兩個(gè)過程[12-13]，分別是三角化過程和標(biāo)準(zhǔn)化過程：（1）三角化過程：運(yùn)用初等行（列）變換將系數(shù)矩陣轉(zhuǎn)化為行階梯型矩陣，如圖3所示，將圖3（a）中對(duì)應(yīng)的矩陣轉(zhuǎn)化為圖3（b）所示矩陣，該矩陣為對(duì)角矩陣；（2）標(biāo)準(zhǔn)化：當(dāng)三角化過程結(jié)束后，運(yùn)用初等行變換將行階梯型矩陣轉(zhuǎn)化為最簡(jiǎn)行階梯型矩陣，如圖3（c）轉(zhuǎn)變?yōu)閳D3（d）所示矩陣。當(dāng)矩陣滿秩時(shí)，系數(shù)矩陣的最簡(jiǎn)行階梯型矩陣即為一個(gè)單位矩陣。將線性系統(tǒng)的系數(shù)矩陣化為單位陣后，即可求得X中對(duì)應(yīng)的輸入數(shù)據(jù)包。

傳統(tǒng)的高斯消元算法只能在當(dāng)系數(shù)矩陣A滿秩時(shí)，才能求解出線性系統(tǒng)對(duì)應(yīng)的未知量X，否則當(dāng)矩陣A的秩小于矩陣的列數(shù)時(shí)，線性系統(tǒng)無(wú)解，也就無(wú)法譯出剩余的輸入數(shù)據(jù)包。但是，經(jīng)觀察發(fā)現(xiàn)，某些情況下，當(dāng)系數(shù)矩陣不滿秩時(shí)，也有可能出現(xiàn)部分未知量可譯的情況，這種情況的例子將在下節(jié)給出，因此本文利用這一特點(diǎn)優(yōu)化了高斯消元算法，以提高BATS碼的譯碼性能。

2 改進(jìn)型的BATS碼高斯消元譯碼算法

在傳統(tǒng)的高斯消元算法描述中，當(dāng)系數(shù)矩陣不是滿秩的情況下，線性系統(tǒng)無(wú)解。但是，通過觀察可以發(fā)現(xiàn)，當(dāng)系數(shù)矩陣不滿秩時(shí)，有些情況下，存在部分未知量可以先行譯出的現(xiàn)象。例如，如圖4所示，對(duì)圖4（a）矩陣采用高斯消元算法。首先，運(yùn)用初等行（列）變換將圖4（a）所示矩陣轉(zhuǎn)化為行階梯型矩陣，得到如圖4（c）所示矩陣，再將圖4（c）所示矩陣轉(zhuǎn)化為最簡(jiǎn)行階梯型矩陣，如圖4（d）所示。在圖4（d）中可以看到，當(dāng)最簡(jiǎn)行階梯型矩陣中存在某一行非零首元為1且同一行中剩下的元素都為零的情況時(shí)，該行所對(duì)應(yīng)的未知量也就是BATS碼中該行所對(duì)應(yīng)的輸入數(shù)據(jù)包一定可以被譯出。

圖4 當(dāng)矩陣不滿秩時(shí)的高斯消元過程

因此，當(dāng)BP譯碼算法停止時(shí)，可以將剩下的批次碼所對(duì)應(yīng)的系數(shù)矩陣合并，計(jì)算該矩陣的秩。如果是滿秩的，則將所有的輸入數(shù)據(jù)包譯出。如果不滿秩，對(duì)其采用高斯消元算法，將系數(shù)矩陣轉(zhuǎn)化為最簡(jiǎn)行階梯型矩陣后，檢測(cè)是否存在可譯出的輸入數(shù)據(jù)包。如果有，則將這些可譯包先行譯出，否則譯碼過程停止。采用這種方法可以提高傳統(tǒng)高斯消元算法的譯碼成功率。為了驗(yàn)證算法的有效性，下面將用Matlab軟件對(duì)傳統(tǒng)高斯消元算法和本位推薦的改進(jìn)型高斯消元算法進(jìn)行仿真和對(duì)比，仿真結(jié)果最終驗(yàn)證了推薦算法的有效性。

3 仿真結(jié)果

考慮如圖5所示為兩跳的刪除信道，s表示發(fā)送端，t表示接收端，刪除概率e=0.2。BATS碼參數(shù)設(shè)置為q=32，L=2，M=4。當(dāng)BATS碼碼長(zhǎng)K為30時(shí)，如圖6所示，橫坐標(biāo)表示發(fā)送端發(fā)送的批次數(shù)，縱坐標(biāo)表示譯碼成功率，譯碼成功率由式K譯碼成功的輸入數(shù)據(jù)包/K計(jì)算得到。圖7為當(dāng) BATS碼碼長(zhǎng)為10時(shí)，傳統(tǒng)高斯消元算法和改進(jìn)型高斯消元算法的譯碼性能比較圖。由圖6和圖7可以清楚看到，改進(jìn)型譯碼算法性能明顯優(yōu)于傳統(tǒng)算法。

圖5 兩跳的刪除信道

圖6 當(dāng)BATS碼碼長(zhǎng)為30時(shí)，傳統(tǒng)譯碼算法與改進(jìn)型譯碼算法的譯碼性能比較

4 結(jié) 語(yǔ)

針對(duì)BATS碼的譯碼提出了一種基于高斯消元算法的優(yōu)化改進(jìn)算法，利用矩陣在不滿秩的情況下仍然可能存在可譯包的事實(shí)，優(yōu)化原有的傳統(tǒng)高斯消元算法，在BP譯碼算法停止后，檢測(cè)到系數(shù)矩陣不滿秩的情況下，不停止譯碼過程，而是繼續(xù)采用高斯消元算法檢測(cè)是否存在可譯包，如果存在則將其譯出。這種方法能夠有效提升BATS碼的譯碼性能，仿真結(jié)果也驗(yàn)證了這一結(jié)論。