帶有引誘角色的多飛行器協(xié)同最優(yōu)制導(dǎo)方法

王少博，郭楊,2,*，王仕成，劉志國，張帥

1. 火箭軍工程大學(xué) 精確制導(dǎo)與仿真實驗室，西安 710025 2. 西北工業(yè)大學(xué) 航天學(xué)院，西安 710072

隨著未來戰(zhàn)場環(huán)境的愈加復(fù)雜和反導(dǎo)武器系統(tǒng)智能化程度的提高，單枚導(dǎo)彈對攔截器的有效突防變得越來越困難，且技術(shù)實現(xiàn)上也變得越來越復(fù)雜。研究者們開始意識到可以采用帶防御器的多導(dǎo)彈協(xié)同制導(dǎo)技術(shù)實現(xiàn)我方導(dǎo)彈的突防與反攔截，因為這種技術(shù)在提高高價值飛行器的突防概率的同時，還可以擴大對攔截器的攔截范圍[1]。本文考慮我方突防器作為引誘角色，攜帶并配合兩枚防御器協(xié)同反攔截敵方攔截器的情形。在后續(xù)的研究中可知這種協(xié)同方式是一種顯式的協(xié)同[2]，它更加深入地考慮了彈間的內(nèi)在聯(lián)系，所以研究這種協(xié)同方式具有重要的現(xiàn)實意義。

就現(xiàn)有的文獻來看，可將協(xié)同制導(dǎo)方式劃分為兩大類：顯式的協(xié)同和隱式的協(xié)同[2]。隱式的協(xié)同，本質(zhì)上是多對一制導(dǎo)中的每個個體，根據(jù)提前設(shè)定好的協(xié)調(diào)參數(shù)，執(zhí)行一對一交戰(zhàn)方案，共同打擊一個目標(biāo)的聯(lián)合行為。例如，Jeon等[3]提出的碰撞時間控制制導(dǎo)律(Impact-Time-Control Guidance,ITCG)制導(dǎo)律，對每一枚導(dǎo)彈預(yù)先指定了一個共同的到達(dá)時間，所有的導(dǎo)彈依據(jù)這個共同時間同時到達(dá)目標(biāo)。相對應(yīng)的顯式的協(xié)同，能夠在制導(dǎo)的過程中考慮并實時協(xié)調(diào)個體之間的內(nèi)在關(guān)系，調(diào)節(jié)整個團隊的某些性能指標(biāo)，降低個體之間差異性，協(xié)同完成作戰(zhàn)任務(wù)。

在多導(dǎo)彈協(xié)同反攔截技術(shù)中比較典型的是三體(突防器-防御器-攔截器)協(xié)同制導(dǎo)問題，三體協(xié)同制導(dǎo)指的是突防器針對來襲攔截器發(fā)射一枚防御導(dǎo)彈，對攔截器進行反攔截以保護自己。最早研究三體協(xié)同制導(dǎo)的是Boyell[4-5]，給出了三體問題的運動學(xué)結(jié)論，推導(dǎo)出了常定方位碰撞過程的閉式關(guān)系。近幾年Ratnoo和Shima、Yamasaki和Balakrishnan率先研究了三體制導(dǎo)問題。Ratnoo和Shima[6]提出了一種防御器利用指令視線角(Command-to-LOS，CLOS)方法的制導(dǎo)律，考慮了各種攻擊幾何和攻擊者機動的情況。后來，他們在文獻[7]中又分析了采用比例導(dǎo)引(PN)制導(dǎo)律和純追擊制導(dǎo)的攻擊導(dǎo)彈對抗采用PN和CLOS策略的防御器的情形，給出了不同情況下的邊界條件。Yamasaki和Balakrishnan[8-9]基于最優(yōu)控制理論和速度誤差反饋，研究了修正的CLOS制導(dǎo)的問題，但是這種方法會造成比較平直的彈道。上述的研究都沒有考慮突防器與防御器的配合，協(xié)同程度較低，是一種隱式的協(xié)同制導(dǎo)方式。考慮到實際戰(zhàn)場環(huán)境中需要實時地對攔截器的運動狀態(tài)進行探測和估計，Shaferman和Shima[10]提出了一種多模自適應(yīng)協(xié)同制導(dǎo)律，將探測估計問題加入到了三體制導(dǎo)中。文中突防器作為引誘角色配合防御器執(zhí)行躲避機動，使得防御器能以較小的能量消耗攔截敵方攔截器。

考慮到制導(dǎo)過程需在有限時間內(nèi)完成，描述末制導(dǎo)過程的模型只有在有限時間間隔內(nèi)才有意義，國內(nèi)的許多學(xué)者開始用有限時間理論[11-12]來設(shè)計制導(dǎo)律。在目標(biāo)對攔截器執(zhí)行引誘機動的情況下，Guo等[11]研究了有限時間約束下的三體攔截制導(dǎo)情形。提出了線性系統(tǒng)輸入輸出有限時間穩(wěn)定(IO-FTS)方法，同時提出了有限時間有界約束下的線性系統(tǒng)IO-FTS的充分條件。在Guo等[11]的基礎(chǔ)上，張帥等[12]提出了一種帶攔截角約束的FTCG協(xié)同制導(dǎo)方法。引入度量矩陣反映系統(tǒng)有限時間輸入輸出的穩(wěn)定性，基于微分矩陣不等式設(shè)計了狀態(tài)反饋控制器，能確保有閉環(huán)系統(tǒng)限時間輸入輸出穩(wěn)定。后來，張帥等在文獻[12]的基礎(chǔ)上，又研究了突防器與兩個防御器相配合并施加一個預(yù)置攔截角的反攔截情形[13]，但是文獻[13]是分離設(shè)置兩個防御器的攔截角的。此外，上述文獻中利用有限時間理論所設(shè)計的制導(dǎo)律都不能得出控制器的解析解。

針對突防器與防御器在制導(dǎo)過程中需要實時協(xié)同，設(shè)計合適的控制器成為必不可少的部分。最常用的方法是采用最優(yōu)控制理論[14-15]和微分對策理論[16]來設(shè)計控制器，這樣設(shè)計出的控制器能夠得出控制輸入的解析解。Shima[14]在考慮單側(cè)最優(yōu)控制問題的基礎(chǔ)上，針對攻擊導(dǎo)彈采用PN、擴展比例導(dǎo)引(APN)和最優(yōu)控制制導(dǎo)律(OGL)這3種情況首先給出了突防器與防御器協(xié)同制導(dǎo)策略，此外又給出了攻擊導(dǎo)彈沒有被防御器攔截時的最優(yōu)一對一目標(biāo)規(guī)避策略。在文獻[14]的基礎(chǔ)上，Prokopov和Shima[15]考慮了針對3種不同協(xié)同方式的線性二次協(xié)同制導(dǎo)策略。結(jié)果表明，突防器-防御器的性能依賴于協(xié)同的方案，驗證了突防器配合防御器機動的協(xié)同方式是最好的。文獻[16]利用微分對策理論提出了一種雙側(cè)最優(yōu)協(xié)同制導(dǎo)律，考慮了突防器-防御器組與攔截器的博弈對抗情形。文中針對任意階線性動力學(xué)問題，采用末端投影變換的方法降低了問題的階數(shù)，簡化了推導(dǎo)的過程。利用線性二次微分對策公式分析了在連續(xù)域和離散域上的任意階線性動力學(xué)問題。Kumar和Shima[17]提出了一種非線性的協(xié)同防御制導(dǎo)律，與之前提出的線性化的方法不同，非線性方法確保了制導(dǎo)策略即使在大的航向角誤差的情況下也是有效的。Weiss等[18]基于所需攻擊者攻擊的最大化脫靶量和目標(biāo)規(guī)避的最小控制提出了兩種制導(dǎo)算法。此外，在考慮不依賴導(dǎo)彈間實時通信的情況下，文獻[19]采用集中式“領(lǐng)彈-從彈”協(xié)同制導(dǎo)架構(gòu)，設(shè)計了從彈的3種末制導(dǎo)律，實現(xiàn)了無導(dǎo)引頭下對目標(biāo)的精確打擊。

從已有的國內(nèi)文獻來看，大多數(shù)集中在對相同角色的多導(dǎo)彈飛行器協(xié)同制導(dǎo)研究中，對不同角色的多導(dǎo)彈的協(xié)同制導(dǎo)研究較少。現(xiàn)有的多導(dǎo)彈協(xié)同反攔截技術(shù)大多考慮突防器和單枚防御器的協(xié)同制導(dǎo)情形，要使得突防器協(xié)同兩枚或多枚防御器對攔截器實現(xiàn)較好的攔截效果還需要深入的研究。此外，還需將諸如引誘[10-15]或探測[19-23]等不同的角色加入到多導(dǎo)彈協(xié)同制導(dǎo)中以實現(xiàn)更加深度的協(xié)同。因此，本文考慮了在制導(dǎo)末端施加相對攔截角的帶有引誘角色的顯式協(xié)同反攔截方案，該方案實現(xiàn)了突防器與兩枚防御器的深度協(xié)同。

綜上，本文在文獻[13,23]的基礎(chǔ)上，基于最優(yōu)控制理論，針對突防器發(fā)射兩枚防御器協(xié)同反攔截來襲攔截器并施加一個相對攔截角的情形，提出了一種帶引誘角色的顯式協(xié)同制導(dǎo)律。相比于文獻[23]提出的隱式協(xié)同，本文在制導(dǎo)律設(shè)計中，考慮了突防器與兩防御器的協(xié)同。相比于文獻[13]，通過建立性能指標(biāo)，求解了突防器和兩防御器三者最優(yōu)控制輸入的解析解。本文設(shè)計的制導(dǎo)律能夠保證兩防御器都能成功攔截攔截器，且能在攔截末端施加預(yù)置的相對攔截角。同時，所設(shè)計的制導(dǎo)律在不同的發(fā)射條件下具有較好的穩(wěn)定性。

1 問題描述

本文考慮一個突防器、2個防御器與一個攔截器交戰(zhàn)的情形。在XI-OI-YI慣性坐標(biāo)系下建立動力學(xué)與運動學(xué)模型。下標(biāo)D1和D2分別表示防御器1和防御器2。a、v、q、r和γ分別表示法向加速度、速度、視線角、相對距離和航向角，下標(biāo)E和P分別表示突防器和攔截器。防御器1和攔截器之間的終端攔截角為γD1+γP，防御器1和攔截器之間的終端攔截角為γD2+γP。當(dāng)2個防御器同時到達(dá)時，它們之間的夾角為γD1-γD2。圖1為突防器、防御器1、防御器2和攔截器之間的運動模型。

圖1 多導(dǎo)彈協(xié)同攔截交戰(zhàn)

從圖1中可以得知在制導(dǎo)末端施加的攔截角是2個防御器之間的相對攔截角。本文的模型是建立在以下的假設(shè)下：

假設(shè)1突防器、防御器1、防御器2和攔截器的模型建立在二維平面質(zhì)點運動空間下。

假設(shè)2假設(shè)突防器、防御器1、防御器2和攔截器的速度恒定，在碰撞三角形成立的條件下，他們的相對運動速度恒定。

假設(shè)3假設(shè)攔截器采用帶有修正項比例導(dǎo)引對突防器進行攔截。

1.1 動力學(xué)與運動學(xué)模型

突防器與攔截器交戰(zhàn)過程可以表示為與突防器相關(guān)的極坐標(biāo)(r,q)的形式，即

(1)

(2)

對式(2)兩邊分別對時間進行求導(dǎo)，可得

(3)

相似地，可以得到防御器與攔截器之間的極坐標(biāo)形式，即

vPcos(γP+qPD1)

(4)

(5)

vPcos(γP+qPD2)

(6)

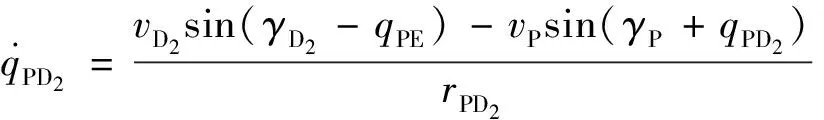
(7)

對式(5)和式(7)兩邊分別對時間進行求導(dǎo)，可得

(8)

(9)

式中：a′Di為aDi在視線上的分量。

(10)

假設(shè)在整個制導(dǎo)過程中，4個飛行器都具有一階線性動力學(xué)特性，則

(11)

式中：aic為飛行器的指令加速度；τi為飛行器的過載響應(yīng)時間常數(shù)。

根據(jù)假設(shè)3，可以得出攔截器制導(dǎo)律，其指令加速度為

(12)

式中：N、K和aPmax分別為攔截器制導(dǎo)過程中的導(dǎo)航參數(shù)、修正系數(shù)和過載限制。

在交戰(zhàn)的后期會形成3個碰撞三角形，它們分別是突防器與攔截器、防御器1和攔截器及防御器2與攔截器之間的。根據(jù)假設(shè)2，一旦碰撞三角形形成，就可以針對非線性運動方程作線性化處理。此時，各視線的法向加速度可表示為

a′E=aEcos(γE0-qPE0)

(13)

a′P=aPcos(γE0+qPE0)

(14)

a′Di=aDicos(γDi0-qPE0)

(15)

突防器與攔截器之間的初始相對距離為rPE0。相似地，防御器1與攔截器之間的初始相對距離為rPD10，防御器2與攔截器之間的初始相對距離為rPD20。在線性化的假設(shè)下，它們之間的相對速度是一個常值，且攔截時間是固定的，滿足:

(16)

(17)

(18)

顯然，確保突防器與防御器1和防御器2成功協(xié)同的必要條件是tfPE>tfPD1，tfPE>tfPD2，當(dāng)t=min(tfPD1,tfPD2)時，制導(dǎo)過程結(jié)束。

通過以上的分析，結(jié)合式(3)、式(8)～式(12)，可以設(shè)定系統(tǒng)的狀態(tài)變量為

(19)

式中：xγ1和xγ2分別為防御器1和攔截器與防御器2和攔截器之間的終端攔截角γD1+γP和γD2+γP。本文中將控制2個防御器在制導(dǎo)末端形成預(yù)置的相對攔截角。

1.2 突防器配合防御器協(xié)同交戰(zhàn)

突防器配合防御器1和防御器2協(xié)同交戰(zhàn)的方式是一種顯式的協(xié)同。在這種情況下，突防器能配合防御器1和防御器2協(xié)同機動，提高攔截性能，由式 (2)、式(5)、 式(7)、式(10)和式(11)可以得到狀態(tài)方程：

(20)

A(t)=

(21)

|uDi|≤uDmax，uDmax為防御器的過載限制。由突防器、防御器1和防御器2的加速度指令組成，即uE=aEC，uD1=aD1C，uD2=aD2C。

相應(yīng)的B(t)可以表示為

(22)

式中:可設(shè)

(23)

(24)

(25)

1.3 突防器不配合防御器協(xié)同交戰(zhàn)

突防器不配合防御器1和防御器2協(xié)同交戰(zhàn)的方式總體來看是一種隱式的協(xié)同。在這種情況下，突防器只負(fù)責(zé)執(zhí)行自己的任務(wù)，不配合兩個防御器進行機動，防御器1和防御器2兩者之間進行顯式的協(xié)同，可以得到狀態(tài)方程

(26)

此時，相應(yīng)的B(t)和G(t)可以表示為

(27)

(28)

其中定義

(29)

(30)

2 最優(yōu)協(xié)同制導(dǎo)律設(shè)計

本文設(shè)計的制導(dǎo)律要滿足在突防器顯式協(xié)同的情況下，防御器1和2可實現(xiàn)對攔截器的有效攔截，使得攔截脫靶量和能量消耗盡量最小，且在攔截終端施加一個相對攔截角。

可將攔截器進入制導(dǎo)盲區(qū)時刻的零效脫靶量作為末端攔截時刻的脫靶量，即

(31)

注1綜合考慮攔截脫靶量、終端攔截角和能量消耗3個方面，本文采用最優(yōu)控制理論設(shè)計制導(dǎo)律。需要設(shè)立包含上述3個方面在內(nèi)的目標(biāo)函數(shù)，依據(jù)目標(biāo)函數(shù)求解突防器與防御器1和防御器2協(xié)同的最優(yōu)控制輸入，滿足制導(dǎo)律設(shè)計的要求。

2.1 目標(biāo)函數(shù)

在本文中考慮一種特殊情況，防御器1和防御器2的攔截時間一致，即tfn=tfPD1=tfPD2。

注2在制導(dǎo)過程中，要求以最小的機動控制要求，在攔截時達(dá)到最小的攔截脫靶量，且施加一個設(shè)定好的終端攔截角γD1-γD2，因此可以得到目標(biāo)函數(shù)為

(32)

權(quán)重系數(shù)α1、α2和β是非負(fù)的，xγi=γT+γi。當(dāng)αi→∞時，可以對攔截器產(chǎn)生完美的攔截。相似地，當(dāng)β→∞時，可以在2個防御器之間產(chǎn)生完美的攔截角。

2.2 模型降階

注3為了降低求解問題的階數(shù)，得到控制輸入的解析解，在此引入終端投影法對模型進行降階處理，引入新的狀態(tài)變量Z(t)。

Z(t)=DΦ(tfn,t)x(t)

(33)

式中：Φ(tfn,t)為與式(21)相關(guān)的狀態(tài)轉(zhuǎn)移矩陣；D為常值向量，用來分離狀態(tài)變量x(t)中的元素。

因為

(34)

結(jié)合式(34)和新的狀態(tài)變量Z(t)對時間的導(dǎo)數(shù)，得到

=DΦ(tfn,t)Bu(t)

(35)

將Dq1、Dq2、Dγ1和Dγ2代入式(33)中，得

Zqi(t)=DqiΦ(tfn,t)x(t)

(36)

Zγi(t)=DγiΦ(tfn,t)x(t)

(37)

式中：i={1,2}；Zqi(t)記為零效脫靶量；Zγi(t)記為零效航向角度。

使用終端投影法降階得到新的變量，式(32)的目標(biāo)函數(shù)可表示為

(38)

3 求解最優(yōu)協(xié)同制導(dǎo)律

3.1 顯式的制導(dǎo)律

在突防器配合防御器1和防御器2協(xié)同交戰(zhàn)的情況下，所設(shè)計的制導(dǎo)律為顯式的制導(dǎo)律。

(39)

式中：

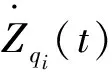
(40)

(41)

目標(biāo)函數(shù)的Hamiltonian函數(shù)為

(42)

由橫截條件得

λZ1=α1Zq1(tfn)

(43)

λZ2=α2Zq2(tfn)

(44)

λZγ1=β[Zγ1(tfn)-Zγ2(tfn)-Δ]=βΔZγ(tfn)

(45)

λZγ2=-β[Zγ1(tfn)-Zγ2(tfn)-Δ]=-βΔZγ(tfn)

(46)

式(45)和式(46)中的ΔZγ(tfn)表示防御器1和防御器2在攔截時的攔截角誤差。

由控制方程得

(47)

(48)

(49)

將式(47)～式(49)分別代入式(40)和式(41)可得

(50)

(51)

(52)

(53)

對式(53)兩邊從t到tfn積分，并整理可得齊次線性方程組Zi(t)=L(t)Zi(tfn)，即

(54)

式中：L(t)為積分后整理得到系數(shù)矩陣。

求解式(54)可得

(55)

(56)

(57)

式中：

N=lq11lq22lγ3-lq11lq23lγ2-lq12lq21lγ3+lq12lq23lγ1+

lq12lq21lγ2-lq13lq22lγ1

將式(55)～式(57)分別代入到式(47)～式(49)中，得

(58)

式中：i∈{E,D1,D2}，導(dǎo)航增益參數(shù)如下：

Zq1(t)和Zq2(t)分別為防御器1和防御器2的零效脫靶量；ΔZγ(t)為防御器1和防御器2相對于攔截器的零效航向角誤差。

3.2 隱式的制導(dǎo)律

在突防器不配合防御器1和防御器2協(xié)同交戰(zhàn)的情況下，所設(shè)計的制導(dǎo)律為隱式的制導(dǎo)律。在設(shè)計制導(dǎo)律時，考慮突防器針對攔截器做最優(yōu)躲避bang-bang機動[14]。根據(jù)突防器與攔截器的相對運動學(xué)，得到兩者之間的狀態(tài)方程。

(59)

式中：

AE(t)=

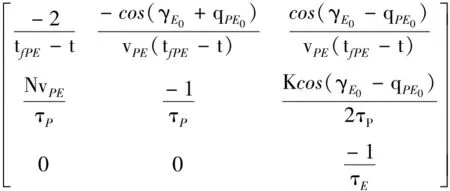
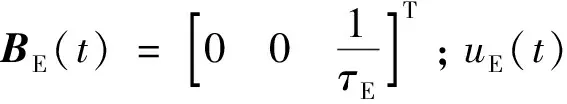
uE=uEmaxsign(sPE)sign(ZPE(t))

(60)

式中：uEmax為突防器的最大指令加速度；

sPE=DEΦ(tfPE,t)BE；ZPE(t)=DEΦ(tfPE,t)xE。

(61)

(62)

(63)

目標(biāo)函數(shù)的Hamiltonian函數(shù)為

(64)

橫截條件與顯式下情形相同，由控制方程得

(65)

(66)

將式(65)和式(66)分別代入式(62)和式(63)可得

[Zγ1(tfn)-Zγ2(tfn)-Δ]

(67)

[Zγ1(tfn)-Zγ2(tfn)-Δ]

(68)

[Zγ1(tfn)-Zγ2(tfn)-Δ]

(69)

[Zγ1(tfn)-Zγ2(tfn)-Δ]

(70)

對式(70)兩邊從t到tfn積分，并整理可得齊次線性方程組Zi(t)=L(t)Zi(tfn)，即

(71)

式中：L(t)為積分后整理得到的系數(shù)矩陣。

求解式(71)可得

(72)

(73)

(74)

式中：

N=lq11lq22lγ3-lq11lq23lγ2-lq12lq21lγ3+

lq12lq23lγ1+lq12lq21lγ2-lq13lq22lγ1。

將式(72)～式(74)分別代入到式(65)和式(66)中，得

(75)

式中：i∈{D1,D2};導(dǎo)航增益參數(shù)如下：

4 仿真分析

在本節(jié)中，將分析第3節(jié)設(shè)計的突防器、防御器1和防御器2三者協(xié)同的最優(yōu)制導(dǎo)律(顯式的協(xié)同)的性能，并與突防器不與兩個防御器協(xié)同的最優(yōu)制導(dǎo)律(隱式的協(xié)同)進行比較。

在仿真中，攔截器采用APN制導(dǎo)律對突防器進行攔截，突防器發(fā)射兩枚防御器對攔截器進行反攔截，所以突防器、防御器1和防御器2的初始發(fā)射位置相等。由先前的假設(shè)可知，防御器1和防御器2的攔截時間相等，所以它們的速度相等。此外，根據(jù)文獻[23]，當(dāng)相對攔截角在30°與65°之間時，兩防御器之間能產(chǎn)生較好的攔截性能，所以本文設(shè)定相對攔截角30°。為具體的仿真參數(shù)可參照表1。

表1 仿真參數(shù)

續(xù)表1

4.1 顯式的協(xié)同

圖2為突防器、防御器1和防御器2三者協(xié)同下的攔截交戰(zhàn)圖。可知，在攔截器對突防器進行攔截時，突防器發(fā)射兩枚防御器對攔截器進行反攔截的同時，執(zhí)行引誘機動，協(xié)助兩枚防御器在坐標(biāo)點(12 950 m, 4 543 m)成功實現(xiàn)對攔截器的反攔截，并在攔截末端形成一個預(yù)置的30°的攔截角。

圖2 顯式的協(xié)同：多導(dǎo)彈協(xié)同攔截交戰(zhàn)

圖3為突防器、防御器1和防御器2的加速度曲線變化圖。可知，在三者的相互協(xié)同下，突防器的最大需用加速度為12.91 m/s2，2個防御器的加速度都達(dá)到了過載限制150 m/s2。當(dāng)敵方攔截器的加速度不受限制時，其最大需用加速度為108.1 m/s2，顯然，此種情形攔截器的作戰(zhàn)效費比較大。此外，在突防器的協(xié)同下，防御器1和防御器2的加速度變化基本相同。這說明，突防器的協(xié)同機動過程可以使得防御器1和防御器2都能同時達(dá)到一個較好的制導(dǎo)效果。此外，圖中顯示在將要達(dá)到攔截點附近時，它們的加速度趨近于0，此時三者均作勻速運動。

圖3 顯式的協(xié)同：加速度的變化

圖4為防御器1和防御器2的能量消耗隨時間變化圖，在10～12 s之間因為加速度變化劇烈，所以消耗的能量增加較快，在12 s以后基本穩(wěn)定下來。在最終時刻防御器1的能量消耗略大于防御器2的能量消耗。

圖5為突防器、防御器1和防御器2的視線角速率變化圖。可知，防御器1和防御器2的視線角速率最終都能穩(wěn)定地收斂到0附近，結(jié)合式(31)可知防御器1和防御器2能以較小的脫靶量攔截攔截器。

圖4 顯示的協(xié)同：能量消耗的變化

圖5 顯式的協(xié)同：視線角速率的變化

圖6為防御器1和防御器2之間的相對攔截角變化圖。可知，防御器1和防御器2在制導(dǎo)過程中不斷調(diào)整它們之間的夾角，并在攔截終端達(dá)到設(shè)定的預(yù)置相對攔截角。圖中的最終相對攔截角為29.84°，與設(shè)定的30°存在0.06°的偏差。

圖7以防御器1為例，視線角速率隨其過載限制的變化圖。可知，隨著防御器過載限制的減小，視線角速率在逐漸減小。根據(jù)式(31)，視線角速率與脫靶量成正比關(guān)系，這說明過大的過載限制會降低防御器的制導(dǎo)性能。同樣地，較大的攔截器過載限制會降低其對突防器的攔截性能。

圖6 顯示的協(xié)同：相對攔截角的變化

圖7 顯式的協(xié)同：視線角速率隨防御器過載限制的變化

4.2 與隱式的協(xié)同進行比較

通過對3.2節(jié)中設(shè)計的隱式協(xié)同制導(dǎo)律進行仿真驗證得到:

圖8為突防器不配合防御器1和防御器2協(xié)同的攔截交戰(zhàn)圖，防御器1和防御器2僅知道突防器未來的機動，無法與突防器進行實時的協(xié)同，且它們兩者協(xié)同施加一個預(yù)置的攔截角。

圖8 隱式的協(xié)同：多導(dǎo)彈協(xié)同攔截交戰(zhàn)

圖9為突防器、防御器1和防御器2的加速度變化曲線，突防器執(zhí)行最大指令加速度為50 m/s2的bang-bang最優(yōu)躲避機動，此時，防御器1和防御器2的加速度均達(dá)到了過載限制值，相比于顯示的協(xié)同，在突防器實行躲避機動的情況下它們的加速度變化比較劇烈，且三者對機動的要求較高。當(dāng)敵方攔截器的加速度不受限制時，其最大需用加速度為147 m/s2，相比于隱式的協(xié)同，顯式的協(xié)同提高了敵方攔截器的作戰(zhàn)效費比。

圖9 隱式的協(xié)同：加速度的變化

圖10 隱式的協(xié)同：能量消耗的變化

圖10顯示了在突防器執(zhí)行最大指令加速度為50 m/s2的bang-bang最優(yōu)躲避機動情況下的防御器1和防御器2的能量消耗圖。由圖中可知，隱式協(xié)同下的兩個防御器的能量消耗遠(yuǎn)遠(yuǎn)大于顯示協(xié)同下的對應(yīng)的防御器的能量消耗。且在隱式協(xié)同下兩防御器的能量消耗相差較大，在12 s之前的制導(dǎo)過程中，兩者的能量消耗一直在快速增加。顯然，顯式的協(xié)同可以大大節(jié)約防御器1和防御器2的能量消耗。

這表明，所設(shè)計的最優(yōu)制導(dǎo)律在突防器配合機動的情況下，能夠有效地減少三者所需的加速度和能量消耗。

圖11顯示了在隱式協(xié)同的情況下，防御器1和防御器2的視線角速率最終能夠收斂到0附近。能夠以較小的脫靶量攔截攔截器。圖12顯示了在隱式的協(xié)同下，防御器1和防御器2能在攔截末端達(dá)到預(yù)置的相對攔截角。

圖11 隱式的協(xié)同：視線角速率的變化

圖12 隱式的協(xié)同：相對攔截角的變化

4.3 不同初始發(fā)射條件對協(xié)同制導(dǎo)律的影響

當(dāng)面對不同的作戰(zhàn)任務(wù)時，防御器也會面臨不同的戰(zhàn)場發(fā)射環(huán)境，所以設(shè)計的制導(dǎo)律在確保制導(dǎo)精度的穩(wěn)定性上顯得尤為重要。基于所設(shè)計的顯式的最優(yōu)制導(dǎo)律，本節(jié)分析了在不同初始發(fā)射條件下的制導(dǎo)性能。當(dāng)防御器從突防器上發(fā)射出去之后，不同的發(fā)射環(huán)境將最終影響初始的視線角速率。

在設(shè)置相對攔截角為30°的情況下，仿真中研究了5種不同的初始發(fā)射條件(初始視線角速率)對制導(dǎo)性能的影響。2個防御器的初始發(fā)射參數(shù)見表2。

表2 初始發(fā)射參數(shù)

圖13和圖14分別為防御器1和防御器2在5種不同初始值情況下的視線角速率變化圖。由圖可知，在5種不同初始值情況下，防御器1和防御器2的視線角速率最終都能收斂到0附近。

圖15為在5種不同初始值情況下的相對攔截角的變化圖。可知，在5種不同的初始值情況下，防御器1和防御器2最終都能在制導(dǎo)末端施加預(yù)置的30°的相對攔截角。

上述仿真驗證了所提制導(dǎo)律的有效性，同時也表明了在不同的發(fā)射條件下，所提制導(dǎo)律能保持較好的穩(wěn)定性。

圖13 防御器1的視線角速率變化

圖14 防御器2的視線角速率變化

圖15 相對攔截角的變化

5 結(jié) 論

1) 針對我方飛行器發(fā)射兩枚防御器有效攔截對方攔截器的突防問題，提出了一種帶引誘角色的顯式協(xié)同制導(dǎo)律，并將其與隱式的協(xié)同制導(dǎo)律進行比較，仿真結(jié)果表明顯式的協(xié)同優(yōu)于隱式的協(xié)同。

2) 所設(shè)計的制導(dǎo)律將脫靶量、能量消耗和施加末端相對攔截角考慮在目標(biāo)函數(shù)的建立中，利用最優(yōu)控制理論求得了不同策略下的控制輸入。

3) 本文沒有考慮制導(dǎo)過程中的探測估計問題，探測效果影響著制導(dǎo)的效果和精度，未來有必要將探測角色加入到協(xié)同制導(dǎo)律的設(shè)計中，實現(xiàn)探測制導(dǎo)一體化設(shè)計。