一種耦合CFD修正的螺旋槳快速設計方法

郭佳豪，周洲，范中允

西北工業大學 航空學院，西安 710072

螺旋槳在飛行器中有著廣泛的應用，為提高飛行器巡航效率，應設計合適且高效的螺旋槳。關于螺旋槳的設計方法，國內外學者已有大量研究。Larrabee[1]提出了最小誘導損失螺旋槳的設計方法。Angelo等[2]提出了根據給定工作狀態和槳葉剖面翼型，快速設計槳葉弦長和扭轉角分布的高效率螺旋槳設計方法。項松等[3-4]在設計時對槳葉截面弦長進行限制，改進了Angelo設計方法獲得的弦長可能過大的缺點，并對設計的螺旋槳進行了風洞試驗。翟若岱[5]應用項松等改進的方法，對臨近空間太陽能飛機的螺旋槳進行了多點設計。

為進一步提高螺旋槳的效率，眾多學者引入優化設計的思想，對螺旋槳槳葉的弦長及扭轉角分布進行優化。許建華等[6]以求解雷諾平均Navier-Stokes方程為螺旋槳氣動性能計算方法，以剖面翼型壓力分布為目標，對螺旋槳平面形狀進行反設計。梁撐剛等[7]將Betz條件和遺傳算法相結合，對無人機螺旋槳槳葉弦長及扭轉角分布進行優化。焦俊等[8]對高空飛艇螺旋槳進行了弦長和扭轉角優化設計，并進行車載試驗。劉芳等[9]采用Xfoil對翼型性能快速求解，首先進行螺旋槳翼型優化，之后對螺旋槳扭轉角分布和弦長分布進行優化，得到高空低雷諾數高效螺旋槳。而Kwon等[10]提出一種螺旋槳多層次優化設計方法：首先對螺旋槳弦長和扭轉角進行優化，得到初始構型；接著對槳葉不同站位的翼型進行優化設計，以提高效率；翼型優化后，再優化弦長和扭轉角，使得效率進一步提高。

此外，Morgado等[11]基于JBLADE軟件，分別采用最大L/D及L3/2/D進行螺旋槳設計，結果表明采用最大L3/2/D設計處的螺旋槳能夠產生更多的升力，且效率更高，其中:L為升力，D為阻力。Yonezawa等[12]針對火星飛行器，對低雷諾數螺旋槳進行設計，并討論了螺旋槳半徑、槳葉個數及前進比對設計結果的影響。

上述螺旋槳設計方法均基于葉素動量理論及渦流理論，不能真實且準確地體現如徑向流動、槳葉槳根及槳尖效應等。而對于太陽能無人機等飛行器應用的螺旋槳，其主要面臨低雷諾數的問題，低雷諾數下槳葉葉素氣動力計算的準確性及槳葉真實三維狀態與設計間的差異，均會對設計的準確性產生較大的影響。一方面會導致螺旋槳真實拉力偏離設計拉力；另一方面，設計狀態下雖然能夠保證螺旋槳效率達到最高，但在真實情況下螺旋槳的高效率并不能夠保證。而若采用CFD求解對螺旋槳進行優化設計，由于單次螺旋槳數值模擬求解便需一定的計算時間，導致設計周期過長。

為解決上述問題，本文在設計過程中耦合數值模擬求解，并以CFD計算結果為參考進行槳葉氣動力反解，以此進行修正與再設計，建立一種螺旋槳快速設計方法，在保證拉力要求下，提高螺旋槳效率。

1 傳統螺旋槳設計方法

傳統螺旋槳設計方法基于最小能量損失[13]。圖1展示了螺旋槳槳葉葉素受力分析，其中，α為葉素實際迎角，β為干涉角，φ0為幾何入流角，φ為實際入流角，W為合速度，W1為誘導合速度，Va1為軸向誘導速度，Vt1為環向誘導速度，V′為誘導螺距。這里假設合速度W與誘導合速度W1垂直。

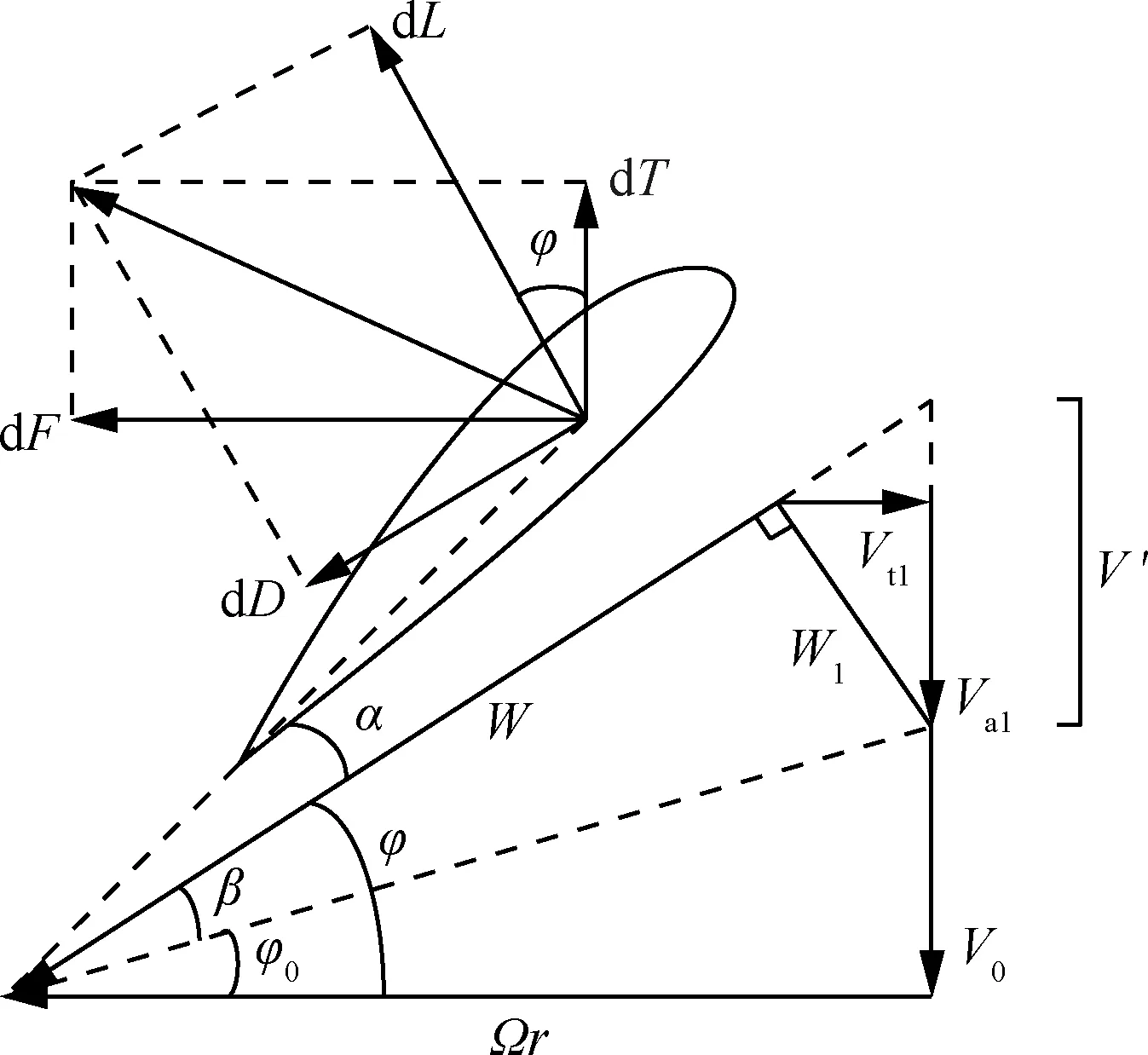
圖1 螺旋槳葉素受力分析

給定設計高度H、來流速度V0、密度ρ、設計拉力T及設計轉速Ω，通過設計得到各葉素合適的翼型、弦長b及實際迎角α。設計過程如下：

1) 確定槳葉數NB，螺旋槳半徑R，將槳葉劃分為N個截面，并確定各截面翼型。

2) 根據設計拉力T及設計狀態求解誘導螺距V′。

最小能量損失下誘導螺距V′沿槳葉為定值[13]。根據渦流理論可知，槳盤徑向r處環向誘導速度與當地環量的關系為

(1)

寬度為dr的葉素產生的拉力dT為

dT=ρΓ(r)(Ωr-Vt1)dr

(2)

由式(1)、式(2)和圖1的幾何關系可得

(3)

則總拉力T為

(4)

其中：f為Prandtl修正因子，即

(5)

故可根據設計狀態及設計拉力，采用Newton迭代求解式(4)得到誘導螺距V′，從而確定各個截面的受力幾何關系，進而得到考慮修正的螺旋槳最佳環量分布：

(6)

3) 求解r處截面的弦長b及扭轉角θ。

根據庫塔-茹科夫斯基定理，葉素升力與當地環量關系為

dL=ρΓ(r)Wdr

(7)

而升力又可表示為

(8)

聯立式(7)和式(8)可得

(9)

式中：CL為升力系數。

葉素工作在最大升阻比下，螺旋槳的效率最高。而根據當地弦長b，可得到對應的雷諾數Re與馬赫數Ma，進而求得葉素截面翼型最大升阻比對應的迎角α及氣動力。根據式(9)迭代求解得到弦長b。對應截面的扭轉角為

θ=α+φ

(10)

限制弦長范圍取為0.02R～0.3R，采用“黃金分割法”求取最接近最佳環量分布的弦長。弦長超過最大限制，則考慮增加槳葉數目。

4) 重復求解，得到所有截面幾何信息。

5) 對弦長b及扭轉角θ分布進行光順處理。

采用四階貝塞爾樣條曲線對弦長b及扭轉角θ分布進行擬合:

p=(1-t)4p0+4(1-t)3tp1+

6(1-t)2t2p2+4(1-t)t3p3+t4p4

(11)

式中：t取值范圍為0～1。

沿槳葉徑向進行積分，可得設計下的螺旋槳總拉力T、扭矩M及效率η分別為

(12)

(13)

(14)

(15)

(16)

式中：CD為阻力系數。

2 數值模擬方法驗證

對于螺旋槳氣動力的求解，相比于動量葉素理論的快速求解方法，CFD方法基于真實模型計算更加接近真實物理狀態，已發展出如多重參考系法、滑移網格及嵌套網格模擬等多種方法。其中多重參考系(Multiple Reference Frames，MRF)法作為一種準定常方法，計算效率高，在螺旋槳數值模擬中應用廣泛[14-16]。

這里以某型太陽能無人機螺旋槳為例，對其分別進行地面試驗與數值模擬。該型螺旋槳槳葉半徑R=0.203 2 m，槳葉數NB=2。地面試驗在無來流狀態下進行，通過改變轉速測量螺旋槳拉力及扭矩的變化。

數值模擬基于MRF法，采用SA湍流模型，通過混合網格技術進行網格生成。其中旋轉域采用四面體非結構網格，網格量為260萬，外流域生成結構網格，網格量為50萬。局部網格如圖2所示。

拉力和扭矩測量結果(EXP)與數值模擬結果(CFD)對比如圖3和圖4所示。可以看出，在較小拉力下，數值模擬結果與試驗測試結果符合較好，驗證了數值模擬方法的可行性，且相比于葉素動量理論，拉力的計算更加準確。

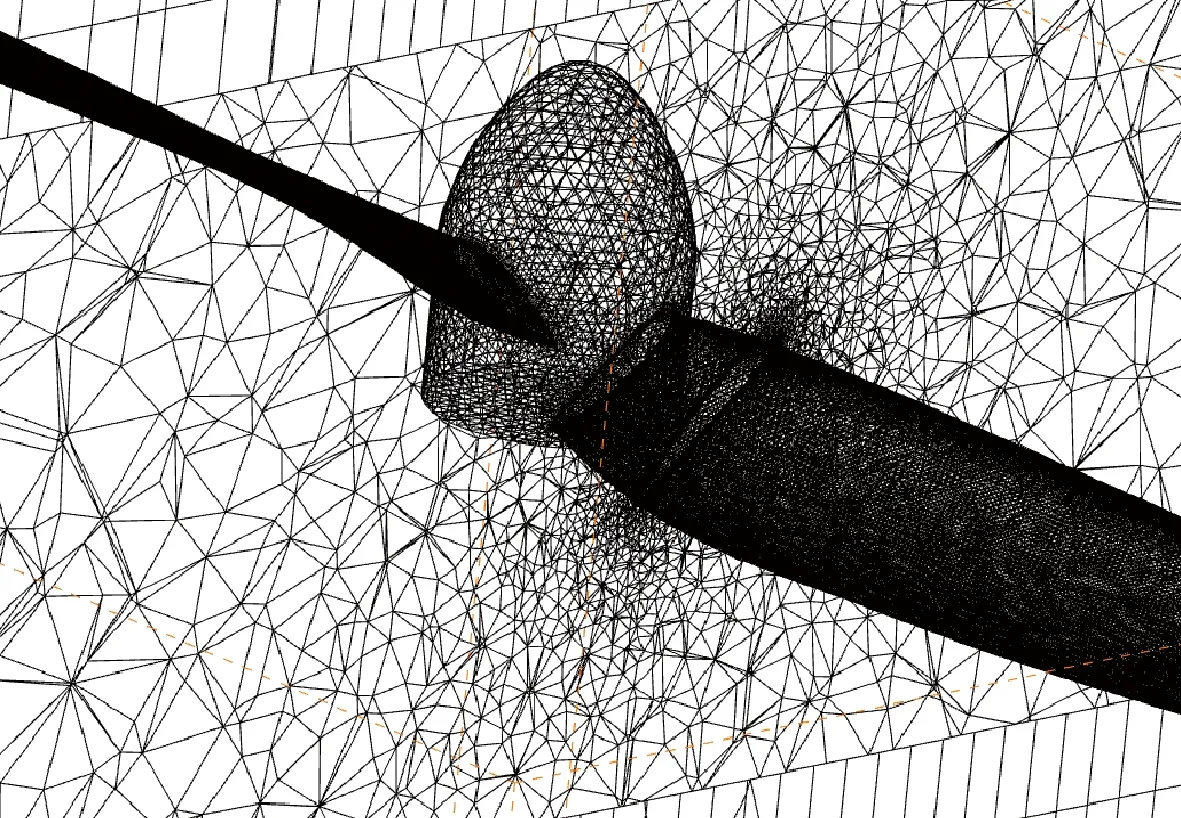
圖2 局部網格示意圖

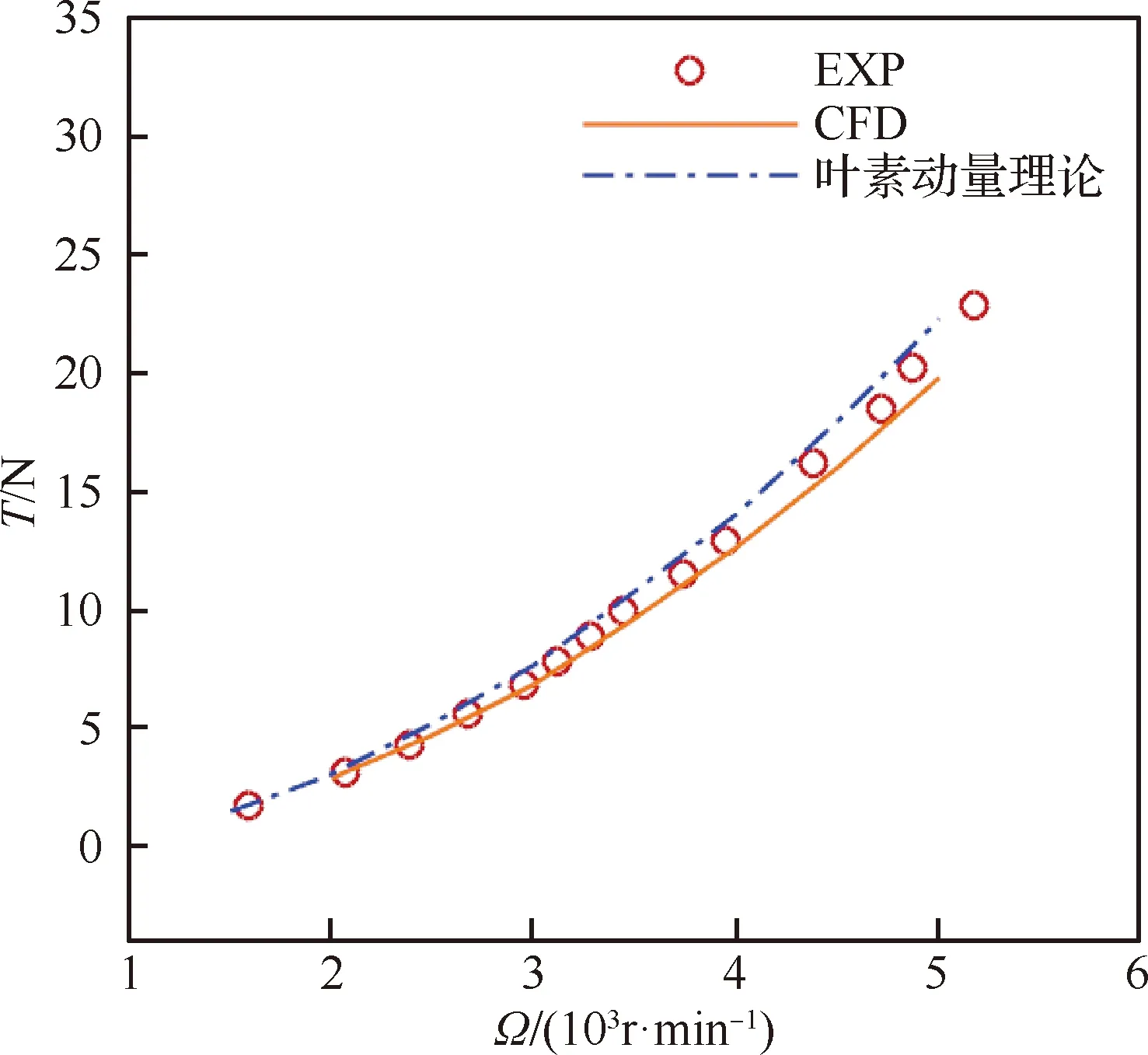
圖3 拉力對比

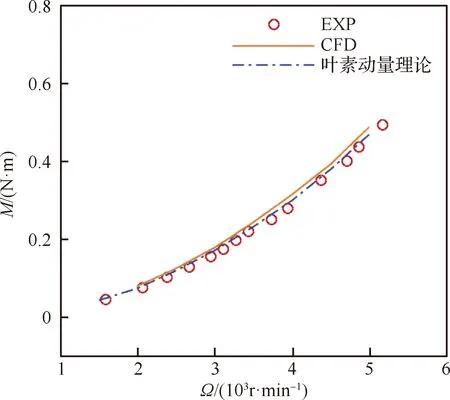
圖4 扭矩對比

3 基于傳統設計方法的螺旋槳設計

3.1 設計狀態

對某型太陽能無人機的螺旋槳進行設計，設計高度H=3 km，來流速度V0=13 m/s，拉力T=10 N，槳盤半徑R=0.27 m。取螺旋槳轉速Ω=2 700 r/min，槳葉數NB=2，槳葉采用Clark Y翼型。

3.2 設計結果

設計得到的螺旋槳弦長、扭轉角分布及三維幾何圖形如圖5所示。主要對0.2R以上的槳葉進行設計，而槳轂至0.2R處做過渡處理。

采用上述螺旋槳方法對設計得到的螺旋槳進行計算，設計結果與CFD計算結果如表1所示，可以看出實際的螺旋槳拉力及效率均小于設計結果，不能滿足設計要求。

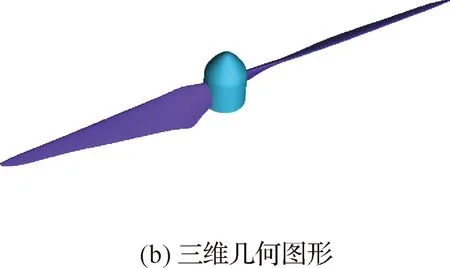
圖5 螺旋槳設計結果

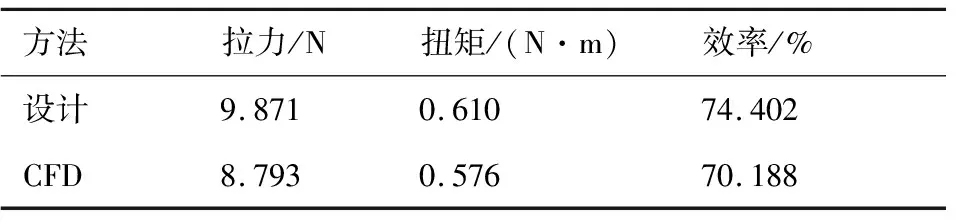
表1 螺旋槳性能對比

4 耦合CFD求解的螺旋槳快速設計

設計結果與真實情況間的差異最終體現在槳葉各葉素截面的氣動力之上，若能夠得到較為準確的葉素截面氣動力，那么一方面設計的拉力較為準確，另一方面設計更接近最小能量損失，可提高螺旋槳效率。因此，本文提出耦合CFD求解的螺旋槳快速設計方法，該方法的主要思想便是：采用CFD數值模擬對設計進行修正，根據CFD的計算結果反解槳葉截面氣動力，之后根據新的氣動力重新設計新的螺旋槳。

4.1 給定葉素氣動力的螺旋槳設計

槳葉各截面采用相同的翼型進行設計時，傳統螺旋槳設計方法得到的沿徑向各葉素截面最大升阻比對應的氣動力如圖6所示。除在槳尖和槳根處存在一定的變化外，沿徑向最大升阻比對應的迎角與升力系數變化不大，而槳尖和槳根處本身的環量偏小，對螺旋槳氣動力的貢獻較低。因此，設計時可視各葉素截面最大升阻比對應的氣動力相同，采用固定的迎角α、升力系數CL及阻力系數CD進行設計。

用固定的迎角、升力系數及阻力系數進行設計時，主要步驟同傳統設計方法。首先根據設計拉力T及設計狀態求解誘導螺距V′。而在求解r處截面的弦長b及扭轉角θ時，由于升力系數CL確定，那么根據式(9)可直接求解弦長，不必進行迭代求解。剩余設計步驟與傳統設計方法一致。

圖6 迎角及升力系數徑向分布

4.2 根據CFD結果反解槳葉素氣動力

假設各葉素截面最大升阻比對應的氣動力相同，對于給定設計狀態及槳葉幾何的螺旋槳，可根據CFD計算得到的拉力及扭矩結果，反解最大升阻比對應的氣動力。步驟如下：

1) 將槳葉劃分為N個截面，根據設計拉力T及設計狀態求解誘導螺距V′，具體步驟同傳統設計方法。

2) 求解最大升阻比對應的迎角α。

根據誘導螺距V′，計算得到第i個截面的實際入流角φi，進而根據式(10)求得迎角αi，故取最大升阻比對應的迎角α為

(17)

3) 已知螺旋槳總拉力T、扭矩M，根據式(12)、式(13)，求得滿足要求的升力系數CL及阻力系數CD。

4.3 耦合CFD修正的螺旋槳設計方法

基于以上方法及分析，提出一種耦合CFD修正的螺旋槳快速設計方法，主要步驟如下：

1) 根據給定的設計狀態，采用傳統螺旋槳設計方法，計算得到初始螺旋槳幾何形狀(弦長及扭轉角分布)。

2) 由于設計采用的葉素氣動力與真實情況存在差異，為保證螺旋槳效率最高，需找到真實情況葉素截面最大升阻比對應的迎角。因此，在初始幾何外形的基礎上，將槳葉的扭轉角整體調整“±θ0”，生成n個螺旋槳外形。接著，采用CFD分別計算其拉力及扭矩，并反解其對應的槳葉葉素氣動力。選取升阻比最大的氣動力數據。

3) 根據選定的數據，通過給定截面氣動力的螺旋槳設計方法，設計新的螺旋槳。

設計流程如圖7所示。

圖7 螺旋槳快速設計流程

4.4 設計結果

在圖5所示傳統方法求得的螺旋槳基礎上，通過整體偏轉扭轉角，得到5個新的構型，對其分別進行CFD求解，并反解氣動力，結果如表2所示。

選取升阻比最大的數據，迎角α=5.819°，升力系數CL=0.864，阻力系數CD=0.041 2，采用給定葉素氣動力的設計方法重新設計。設計結果如圖8所示。

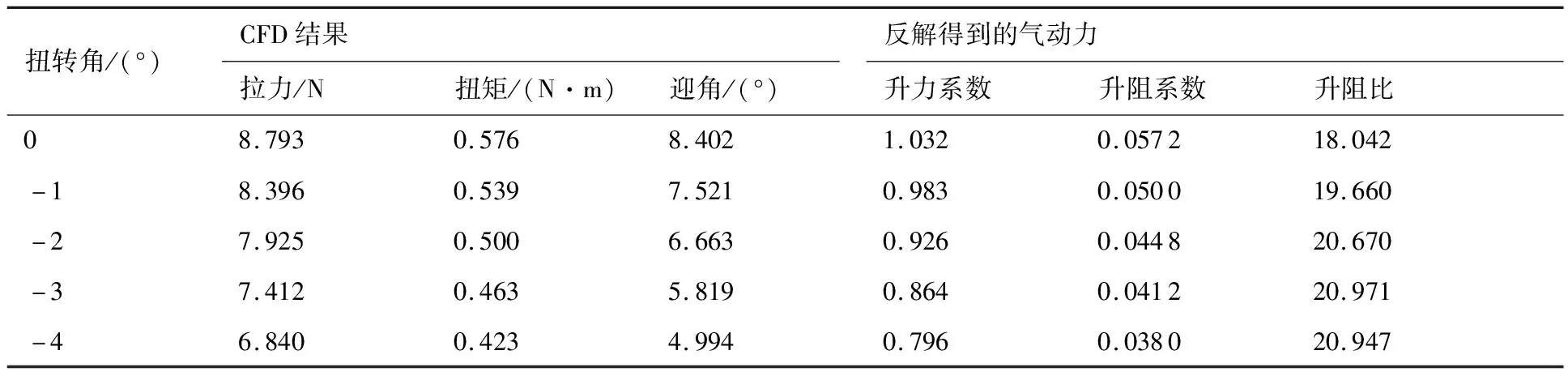
表2 CFD結果及反解得到的氣動力

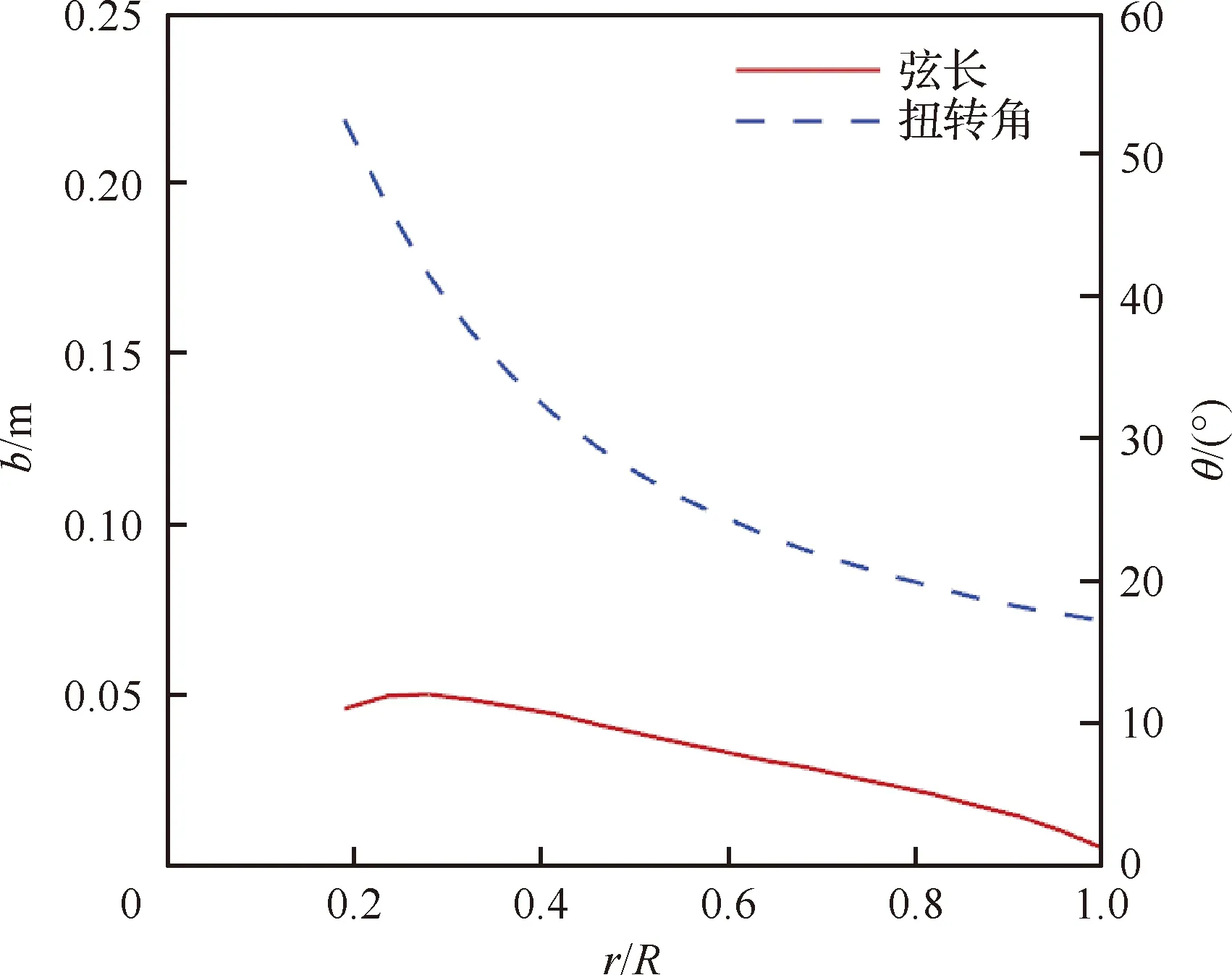
圖8 新設計方法所得弦長與扭轉角分布

采用CFD方法計算其氣動力，并與傳統設計結果進行對比，如表3所示。在設計點處，本文提出的設計方法，一方面能夠較好地滿足拉力要求，另一方面相比于傳統設計方法，設計得到的螺旋槳效率提高2.75%。在非設計點，大前進比(λ)下設計得到的螺旋槳拉力及效率略小于傳統方法設計結果，而前進比小于0.6時，螺旋槳的拉力及效率均優于傳統方法設計結果，如圖9所示。驗證了設計方法的可行性。

表3 傳統和新設計方法螺旋槳設計點性能對比

圖9 傳統和新設計方法螺旋槳性能對比

5 考慮翼型優化的螺旋槳設計方法

為進一步提高螺旋槳效率，在前文提出方法的基礎上，對螺旋槳翼型進行優化。

5.1 優化方法

采用“代理優化”[17]方法對螺旋槳翼型進行優化。文中采用的代理優化方法基于“Kriging代理模型”[18]，子優化方法采用“遺傳算法+乘子法”。遺傳算法采用擬二進制交叉、多項式變異、最佳保留策略及聯賽選擇；乘子法采用Rockfellar推廣的乘子法;并在優化過程中采用“最小代理模型預測準則[17](Minimum of Prediction, MSP)+改善期望準則[19](Expected Improvement, EI)”兩種加點法則更新代理模型。

文獻[20]研究表明：Xfoil在低雷諾數下求解精度雖不及采用高級湍流模型的CFD方法，但其本身具有一定的精度。且對于翼型的優化，更關注其相比于原翼型的改進趨勢，因此對翼型采用Xfoil快速求解，這也能夠節省大量設計時間。而翼型采用“CST參數化方法”[21]。

5.2 優化目標及約束

對于上文采用耦合CFD修正設計得到的螺旋槳，選取0.2R、0.5R及0.8R這3個槳葉截面，優化迎角α=5.819°狀態下的翼型氣動力，對應的雷諾數分別取為50 000、70 000、90 000。

優化目標：平均阻力最小，即MinC′D，且

C′D=(CD1+CD2+CD3)/3

(18)

式中：CD1對應第1個狀態的阻力系數。這里對阻力進行優化的原因是，低雷諾數下阻力的變化更加劇烈，優化的空間更大。

約束條件：平均升力不減小，C′L≥C′L0，下標0代表基礎翼型；翼型面積不減小，A≥A0；翼型最大厚度不減小，t≥t0。

5.3 翼型優化結果

優化過程收斂曲線如圖10所示。優化前后翼型對比如表4和圖11所示。優化后的翼型最大厚度和面積略有增加，后緣彎度增大。從圖11中可以看出，優化后翼型前緣上表面的低壓降低，后緣下表面的高壓增大，因此阻力的降低隨之帶來翼型升力的提高，這也是采用“升力不減小”而非“升力不變”約束進行翼型優化的原因，圖中:Cp為壓力系數。

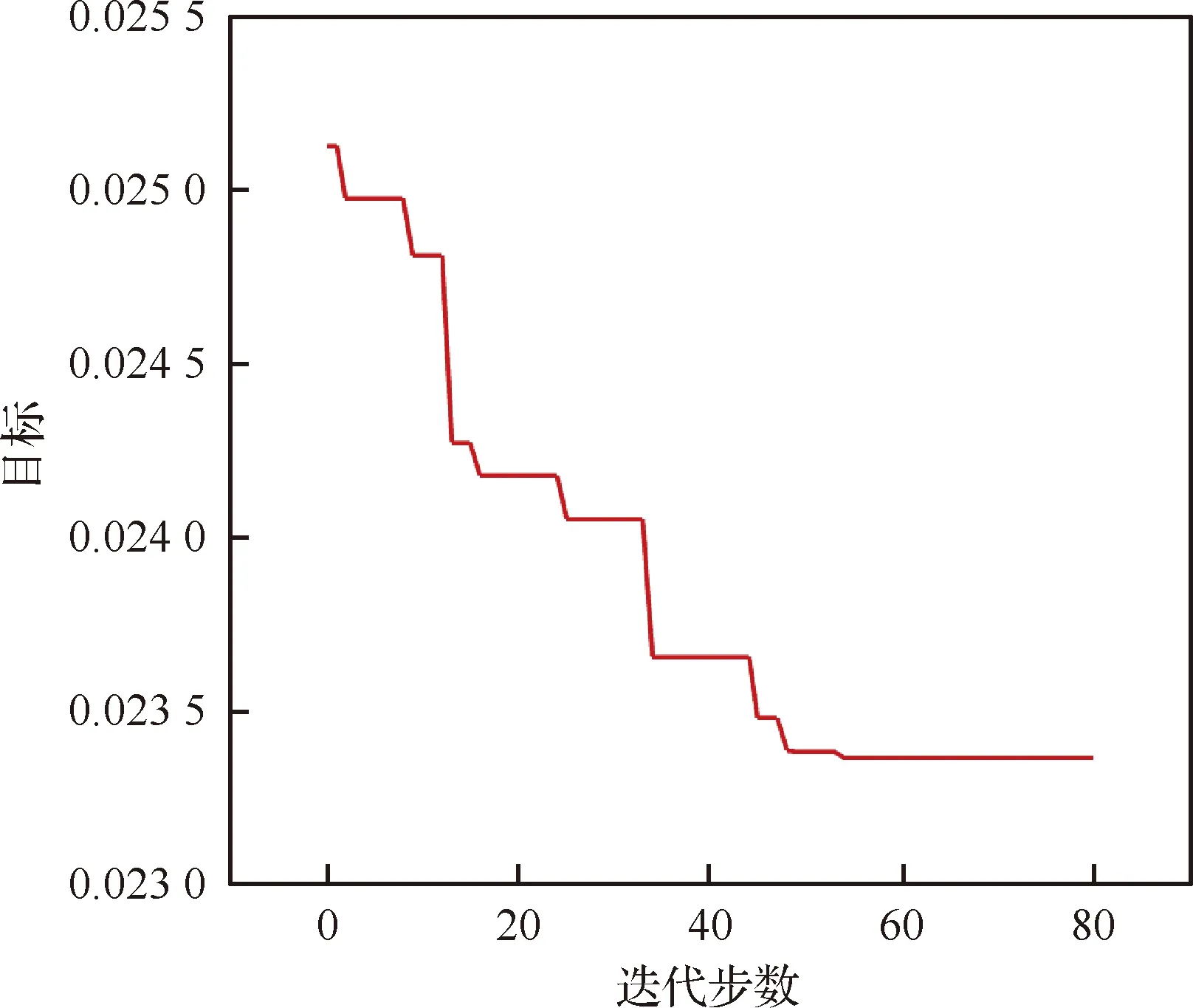
圖10 優化收斂曲線

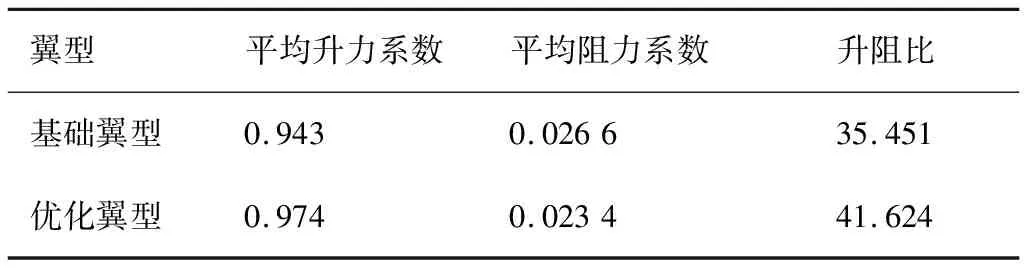
表4 翼型優化前后氣動力對比

圖11 優化前后翼型壓力分布對比(Re=50 000)

5.4 螺旋槳優化設計流程

考慮翼型優化的螺旋槳快速設計流程如圖12所示，優化前后翼型外形對比如圖13所示。得到優化翼型后，在耦合CFD修正的設計結果上替代基礎翼型，生成新的螺旋槳并進行計算。因為對翼型優化時只限制升力的下限，故會存在升力系數變化的情況，此時得到的拉力則會偏離設計拉力。并且新的翼型應用在槳上后，其葉素截面最大升阻比對應的迎角也無法保證與基礎翼型一致。因此，需再次通過改變槳葉扭轉角生成不同螺旋槳，根據CFD計算結果進行反解氣動力及再設計，從而得到滿足設計要求的高效螺旋槳。

圖12 考慮翼型優化的螺旋槳快速設計流程

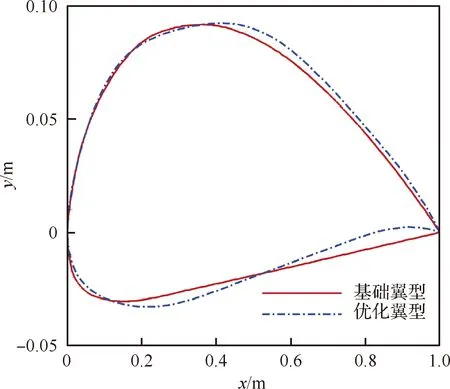
圖13 優化前后翼型外形對比

5.5 螺旋槳性能對比

反解得到葉素截面最大升阻比對應的最佳氣動力特性包括：α=4.565°，CL=0.835，CD=0.036 4。再采用該氣動力重新設計，得到如圖14所示結果。

表5及圖15展示了3種設計方法得到的螺旋槳性能對比。考慮翼型優化的設計方法，能夠在滿足拉力要求的同時，進一步提高螺旋槳效率。在設計點處，相比于傳統方法，效率提高3.95%。

圖14 優化翼型前后設計結果對比

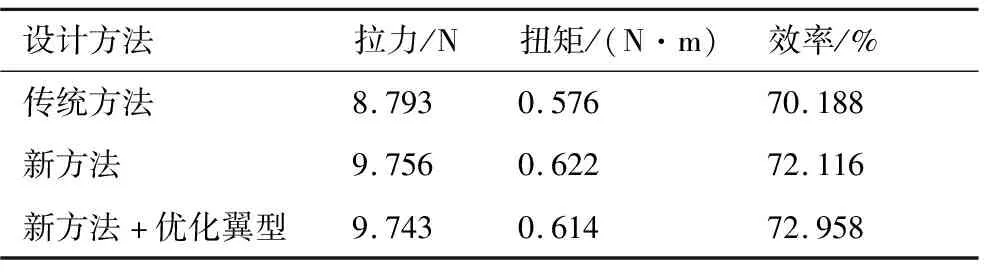
表5 不同設計方法螺旋槳設計點性能對比

圖15 不同設計方法螺旋槳性能對比

6 結 論

本文根據CFD計算對螺旋槳的設計進行修正，提出一種能夠較好滿足設計拉力要求的高效螺旋槳設計方法，得到的結論如下：

1) 傳統螺旋槳設計方法存在一定缺陷。首先，設計得到的螺旋槳其真實的拉力與目標拉力存在一定偏差；其次，不能保證真實情況下槳葉葉素截面的升阻比最大，因此不能保證設計螺旋槳的高效率。

2) 將設計與實際情況葉素氣動力的差異，以及真實情況下如展向流動、槳葉槳根及槳尖處的三維效應帶來的影響，歸結于螺旋槳槳葉氣動力的改變。提出了根據給定氣動力進行螺旋槳設計的方法。假設槳葉葉素截面最大升阻比對應的氣動力沿徑向不變，通過整體改變螺旋槳扭轉角，生成多個螺旋槳構型，再通過CFD計算及反解氣動力，可得到升阻比最大的氣動力數據。根據該數據進行螺旋槳的再設計，可得到高效率的螺旋槳。

3) 經過實例的對比分析，文中所建耦合CFD求解的螺旋槳設計方法，一方面能夠較好地滿足設計拉力要求，另一方面相比于傳統設計方法，設計得到的螺旋槳效率提高了2.75%。而采用代理優化的方法對螺旋槳翼型進行優化后，相比于傳統設計方法螺旋槳的效率可進一步提高3.95%。此外，該方法只需進行少量的CFD計算即可，計算量遠小于直接采用數值模擬優化螺旋槳弦長及扭轉角分布的方法。