等傾干涉條紋與牛頓環的比較
楊小云 趙娟

摘? 要:薄膜干涉是大學物理和光學課程中一種非常重要的光學現象,薄膜干涉可以分為等傾干涉和等厚干涉。該文針對等傾干涉條紋和牛頓環的形成原理和特點進行了分析,比較了這兩種明暗相間的同心圓環條紋的半徑和間距、條紋的級次、條紋的移動規律,得出了這兩種形狀相似而實質不同的干涉條紋的區別和聯系,有助于學生理解和掌握。
關鍵詞:等傾干涉? 等厚干涉? 牛頓環? 干涉條紋
中圖分類號:O436.1 ? ?文獻標識碼:A 文章編號:1672-3791(2020)01(a)-0227-02
薄膜干涉作為光的一種干涉現象,應用非常廣泛,可用于光學元件表面的檢驗、長度或角度的精密測量及高分辨率的光譜分析[1]。在光學教學中,薄膜干涉分為等傾干涉和等厚干涉,而等傾干涉條紋和牛頓環都是內疏外密的同心圓環,這兩種干涉條紋是否完全一樣呢?下面就它們的形成原理、條紋的半徑和間距、條紋級次和移動規律進行比較。
1? 等傾干涉
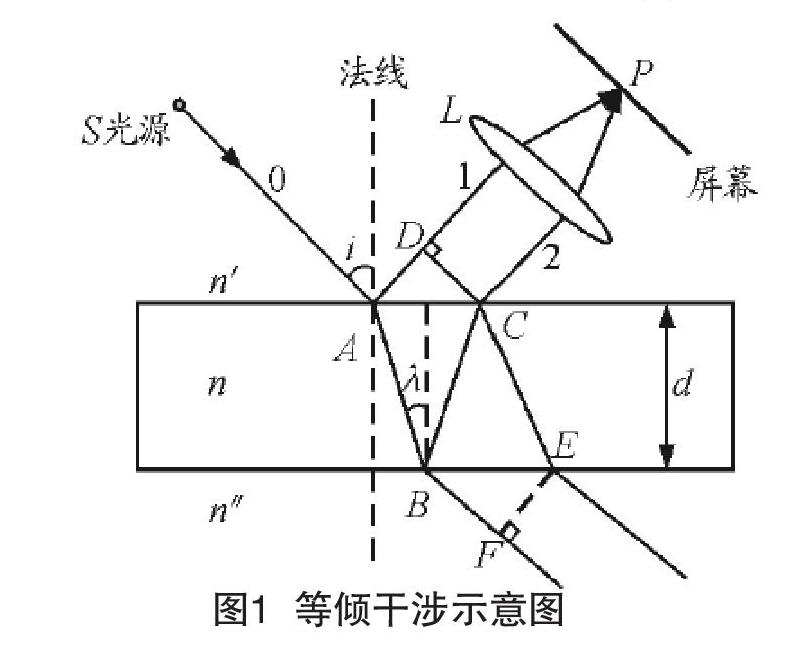
等傾干涉是擴展光源照在折射率均勻、上下表面平行的薄膜上產生的干涉,薄膜可以是透明的固體、液體或氣體薄層。如圖1所示,一束入射光0經薄膜上下兩表面分別反射和折射,最后從薄膜上表面出來的兩束光1和2都在薄膜的同一側,都來自于同一束入射光,因此這兩束光是相干光,經過會聚透鏡后會聚到一點,由于入射角相同的光經過薄膜兩表面反射和折射后最后在相遇點有相同的光程差,形成同一條紋,不同傾角的入射光形成一組干涉條紋,故這種干涉稱為等傾干涉,條紋是一系列明暗相間的同心圓環。
1.1 條紋的半徑和間距
第k級暗紋對應的傾角為i,則有[2]:
2ndcosi=kλ ? ? ? ? (1)
若條紋中心(i=0)的干涉級為m,則:
2nd=mλ ? ? ? ?(2)
從中心往外數的第j個環的干涉級為m-j級,所以:
2ndcosij=(m-j)λ ? ? ? ?(3)
根據泰勒公式cosi=i2/2!+i4/4!-…,入射角很小時,可略去高階小量,則有:
(4)
設會聚透鏡的焦距為f,第j個暗環的半徑為:
(5)
對上式微分,可得第j個暗環附近相鄰兩環的間距為:
(6)
1.2 條紋級次
由公式(1)知,在條紋中心處,光程差最大,干涉級次最高,但條紋不一定是明紋或暗紋,從中心往外,光程差是逐漸縮小的,干涉級次依次降低,故條紋是內環的級次高而外環的級次低[3]。
1.3 干涉條紋的移動規律
當薄膜的厚度連續增大時,光程差連續增加,因此同一位置處的干涉級會連續增大,由(6)知,條紋會越來越密,因此條紋從中心一個個向外冒出;當薄膜的厚度連續減小時,將會與上述情況相反:條紋從外向內移動并一個個陷入中心,并且條紋間距越來越疏。
2? 等厚干涉
等厚干涉是擴展光源照在折射率均勻、上下表面不平行的薄膜上產生的干涉,入射角相同、薄膜厚度相同的各點對應著相同的光程差,形成同一級干涉條紋,只有厚度不同的薄膜才能形成一組干涉條紋,條紋的形狀反映了薄膜等厚點的軌跡,故這種干涉稱為等厚干涉。典型的有楔形平板干涉和牛頓環,其中牛頓環與等傾干涉條紋易形成混淆,這里我們選用牛頓環進行比較。
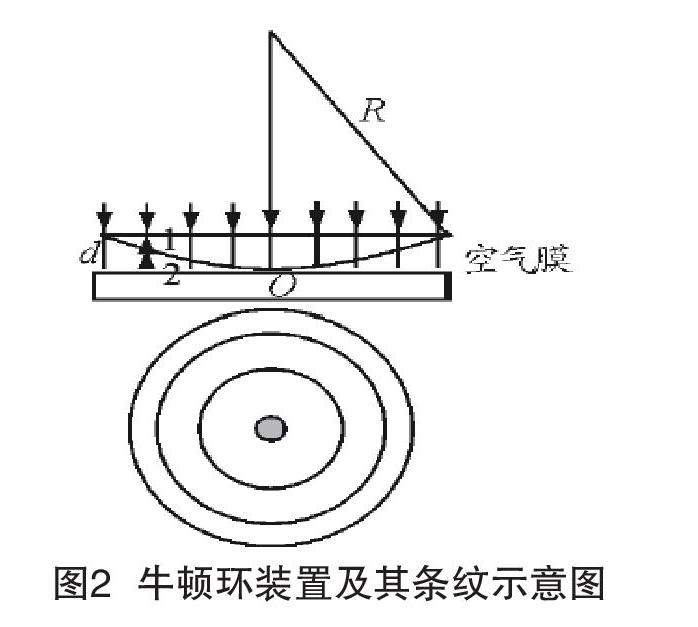
如圖2所示,在一塊平面玻璃板與一塊曲率半徑很大的玻璃平凸透鏡之間形成一個上表面是球面、下表面是平面的空氣薄膜,當用單色的平行光束垂直照射時,兩相干光在相遇點的光程差取決于該處空氣薄膜的厚度,借助顯微鏡從上往下觀察會看到一組以接觸點為圓心的明暗相間的同心圓環,因此稱為牛頓環。
2.1 條紋的半徑和間距
在反射光中觀察牛頓環,第j個暗環的半徑為[2]:
(7)
式中,R為平凸透鏡的曲率半徑,λ為入射光的波長,對上式微分,可得第j個暗環附近相鄰兩環的間距為[4]:
(8)
2.2 條紋級次
在牛頓環中心處,光程差最小,干涉級次最低,因此中心是一暗斑。由公式(7)(8)知,離開中心越遠,半徑越大,干涉級次越高,條紋越來越密,故牛頓環是內環的級次低而外環的級次高。
2.3 干涉條紋的移動規律
當空氣膜的厚度連續增大時,光程差連續增加,因此同一位置處的干涉級會連續增大,由(8)知,圓環會越來越密,因此圓環從外向內移動并一個個陷入中心;當空氣膜的厚度連續減小時,將會與上述情況相反:圓環從中心一個個向外冒出,并且圓環間距越來越疏。
3? 結語
等傾干涉條紋和牛頓環都是明暗相間的同心圓環,間距都是內疏外密,但它們具有本質的不同:(1)條紋的半徑和間距雖然形式相同,但并不完全一樣;(2)干涉級次不同。等傾干涉條紋級次是內高外低,而牛頓環級次恰恰相反;(3)干涉圖樣的中心不同。等傾干涉條紋的中心不一定是明紋或暗紋,而牛頓環中心通常是暗斑;(4)改變膜層的厚度時,干涉條紋的移動規律不同。當膜層厚度連續增大時,等傾干涉條紋從中心一個個向外冒出,而牛頓環一個個往中心收縮;當膜層厚度連續減小時,將會出現與上述相反的情況。
參考文獻
[1] 童元偉,顧錚,卜勝利.牛頓環與等傾干涉教學中的一點體會[J].大學物理,2013,32(12):34-36.
[2] 姚啟均.光學教程[M].5版.北京:高等教育出版社,2014:35-54.
[3] 張燕飛.談等傾干涉和等厚干涉的異同[J].黃山學院學報,2005,7(3):30-31.
[4] 何熙起.牛頓環與等傾干涉條紋比較[J].海南師范學院學報,2006,19(4):332-334.

