布置方案對近海小型無人監測船波浪運動的影響

路驕陽， 岳前進， 張大勇， 蘇學榮

(1.大連理工大學 海洋科學與技術學院， 遼寧 盤錦 124221； 2.北部戰區海軍91040部隊， 山東 青島266000)

0 引 言

海洋覆蓋地球表面的70%以上，包含地球上大約90%的生命形式。它們是食物、就業和經濟收入的主要來源之一，是仍然未知的生物、礦產資源以及可持續能源的潛在來源[1]。在人類開發和可持續利用海洋資源的過程中，海洋監測技術是一種必不可少的手段，發展海洋監測技術具有重要意義。例如：海洋能源的開發需要及時、準確地觀測預報服務[2-3]；建設海洋牧場、修復海洋漁業資源需要加強對海洋環境的監測[4]；保護海洋環境、治理海洋污染需要發展污染和生態環境監測技術，提高監測能力[5]。

傳統的海洋監測手段包括船舶走航、衛星遙感、沿岸監測站、海洋浮標等[6]。每種方法都有一定的局限性：船舶走航測得的數據樣本少，周期長，成本高；衛星遙感準確度不高，可測參數種類少；沿岸監測站只能獲取近海資料；海洋浮標的設計、布置和維護均比較困難[7-8]。近年來，隨著人工智能技術、控制技術、導航定位技術的飛速發展，無人監測平臺成為海洋監測技術的一大研究熱點[9]。

小型無人監測船具有成本低、作業高效、工作范圍廣、數據可靠等一系列優點。然而，由于近海海域水深較淺、離陸地較近，波浪、海流等容易受地形因素的影響，形成較為復雜的海洋環境[10]。另外，由于自身尺度原因，小型無人監測船極易在波浪中發生較大幅度的運動，這些運動輕則會導致傳感器測出的數據不夠準確，無法正常工作，重則可能導致儀器損壞，甚至使船發生傾覆。因此，如何減小小型無人監測船在波浪中的運動，是設計者必須考慮的問題。然而，目前國內外針對小型無人監測船的研究大多集中于避障[11]、運動控制[12]、路徑規劃[13]等技術，針對船體波浪運動性能的相關研究較少，在船體設計過程中，船廠大多借鑒游艇、玻璃鋼游樂船的相關設計經驗[14]，產品運動性能較差，可靠性不高。

以一艘近海小型雙體無人監測船為例，采用二維切片法進行數值計算，分析吃水深度、橫搖慣性矩、縱搖慣性矩、重心高度對近海小型無人監測船波浪運動的影響，得出一系列結論，可為小型無人監測船布置方案設計提供參考。

1 船型參數及數值計算方法

1.1 船型主尺度

與傳統單體船相比，雙體船寬度更大，具有甲板開闊、橫搖穩心半徑大、興波阻力小、耐波性好等一系列優點[15]，因此市場上的小型海洋無人監測船多采用雙體船的結構型式。考慮到這一因素，以大連理工大學海洋科學與技術學院自行設計的小型雙體無人監測船為例進行相關計算分析，其主尺度如表1所示。

表1 自行設計的小型雙體無人監測船主尺度 m

無人監測船需搭載的主要設備包括：環境監測相關傳感器、電池、推進器、控制板等。船體模型如圖1所示。

圖1 小型雙體無人監測船模型

1.2 數值計算方法

船舶搖蕩運動是一種六自由度運動，分別稱為橫搖、縱搖、艏搖、橫蕩、縱蕩和垂蕩，其中橫搖、縱搖、垂蕩對無人監測船工作影響最大。本文的計算過程主要關注這3個自由度的運動響應。

目前在船舶水動力研究領域，主要采用流體力學中的勢流理論對船舶在波浪中的運動響應進行預測，具體包括基于平面勢流理論的切片法、基于三維勢流理論的面元法等。二維切片理論的優勢在于：在浮體滿足細長體假設的前提下，可以運用頻譜分析方法預報不同波長、浪向和航速的浮體在給定波譜下的運動。該理論計算過程耗時較少，精度結果比較理想。考慮所用模型滿足細長體假設，故使用二維切片法對無人監測船進行頻域分析，水動力模型如圖2所示。具體計算理論在文獻[16-17]中已有詳細的描述，不再贅述。

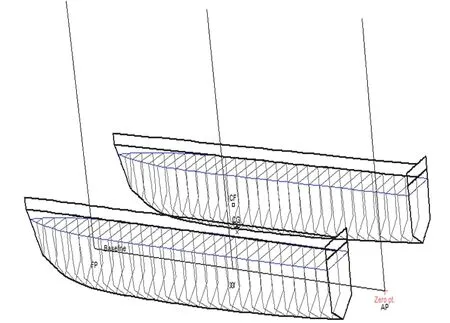
圖2 無人監測船二維切片法模型

2 計算結果及分析

該小型無人監測船主要應用于渤海，取波浪角為45°，計算并分析不同布置方案，包括吃水深度、橫搖慣性矩、縱搖慣性矩、重心高度等對其運動性能響應的影響。

2.1 吃水深度對無人監測船運動性能的影響

無人監測船吃水深度直接關系到可搭載設備的種類與數量。在安全范圍內，盡量增加無人監測船的吃水深度，搭載更多環境監測傳感器，可提高經濟效益。本節詳細分析吃水深度對無人監測船運動性能的影響，以期為無人監測船設計過程中吃水深度的選取提供參考依據。

針對上述無人監測船模型，在計算過程中，保持無人監測船重心高度、橫縱搖慣性矩不變，設置吃水深度分別為0.10 m、0.15 m、0.20 m、0.25 m和0.30 m，對其橫搖、縱搖、垂蕩等3個自由度的運動響應進行分析。

幅值響應因子也稱為傳遞函數，描述了浮體運動響應如何隨波浪頻率變化，是浮體運動性能的重要表征參數。在計算與分析過程中，重點關注這一參數隨吃水深度變化的規律，具體結果如圖3～圖5所示。

圖3 吃水深度對橫搖運動的影響

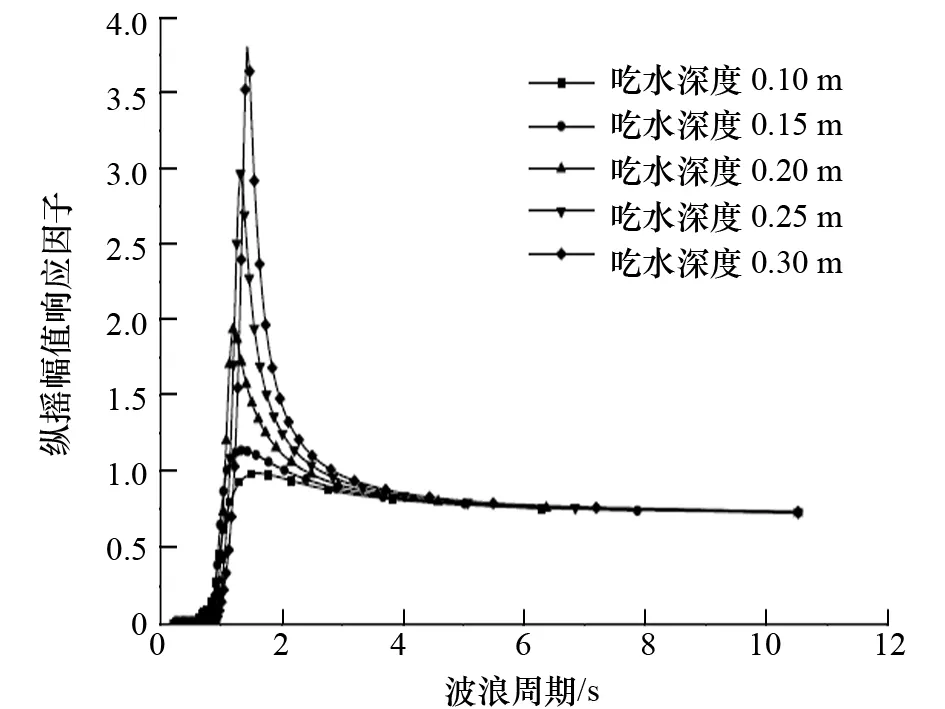
圖4 吃水深度對縱搖運動的影響

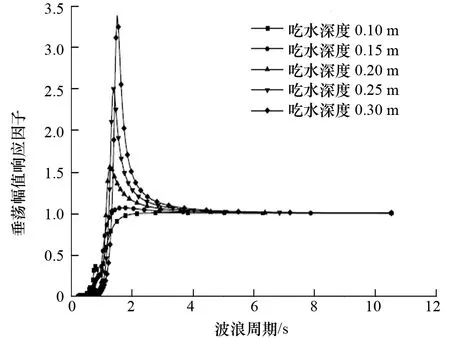
圖5 吃水深度對垂蕩運動的影響

分析圖3～圖5中各自由度的運動響應因子隨吃水深度的變化情況可以發現：

(1) 吃水深度對3個自由度的運動性能均有一定影響。隨著吃水深度增加，橫搖、縱搖、垂蕩運動逐漸增大，響應幅值先向高頻再向低頻移動。

(2) 當吃水深度超過0.2 m后，各自由度運動響應隨吃水深度增加而急劇增大。

(3) 各自由度最大幅值響應對應的周期大致在1～2 s，這一結果已遠離渤海海浪能量集中區4.5～4.8 s[17]。當波浪周期大于3 s后，運動響應已處于較低水平。

(4) 吃水深度對縱搖、垂蕩運動的影響略微大于對橫搖運動的影響。

根據上述結果，在設計無人監測船吃水深度時，由于吃水深度對3個自由度的運動響應均具有明顯影響，應對3個自由度的運動響應進行綜合考量。在通常情況下，在一定范圍內考慮對吃水深度進行適當增加。無人監測船運動響應雖會隨吃水深度增加而增加，但增幅并不明顯，仍處于安全范圍。在超過這一范圍后，增加無人監測船的吃水深度會使3個自由度運動響應急劇增加，在遭遇低周期海浪時可能會發生危險。

2.2 慣性矩對無人監測船運動性能的影響

慣性矩與無人監測船搭載儀器在相應方向上的布置有關。研究慣性矩對無人監測船運動響應的影響可以為無人監測船搭載儀器在相應方向上的布置方案提供依據。引入參數k表征慣性矩相對于長度和寬度的百分比，其表達式為

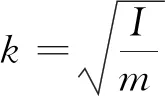
(1)

式中：I為對應方向的慣性矩；m為物體質量。

在計算橫搖慣性矩影響的過程中保持無人監測船重心高度、縱搖慣性矩、吃水深度不變，設置k分別為10%、20%、30%、40%、50%、60%，計算結果如圖6～圖8所示。

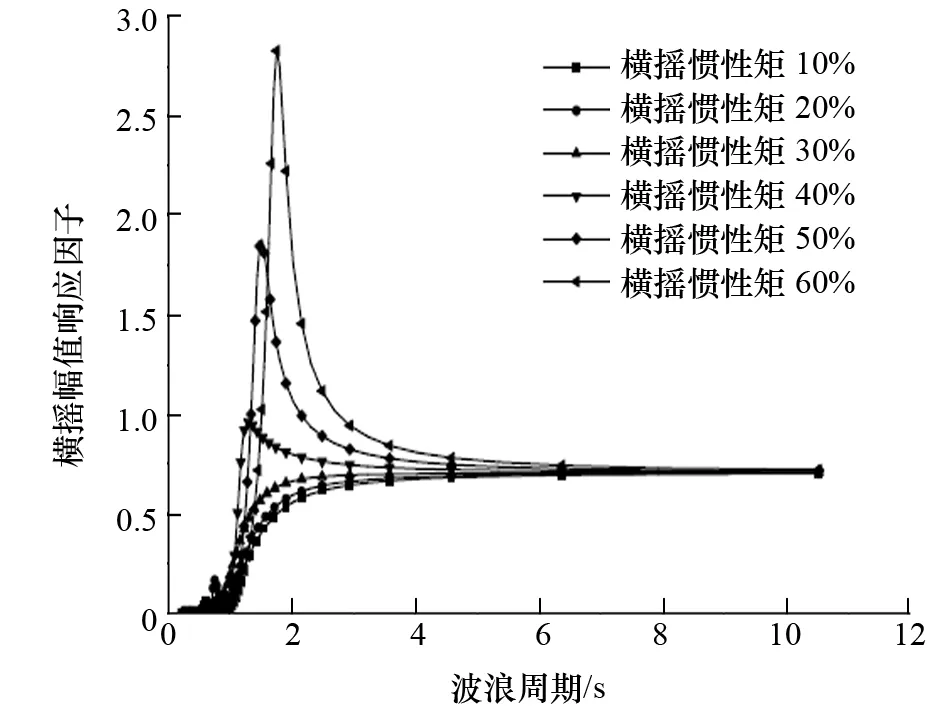
圖6 橫搖慣性矩對橫搖運動的影響

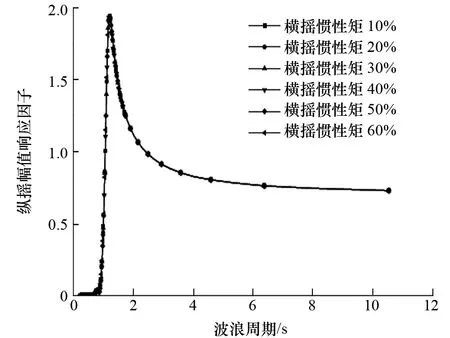
圖7 橫搖慣性矩對縱搖運動的影響

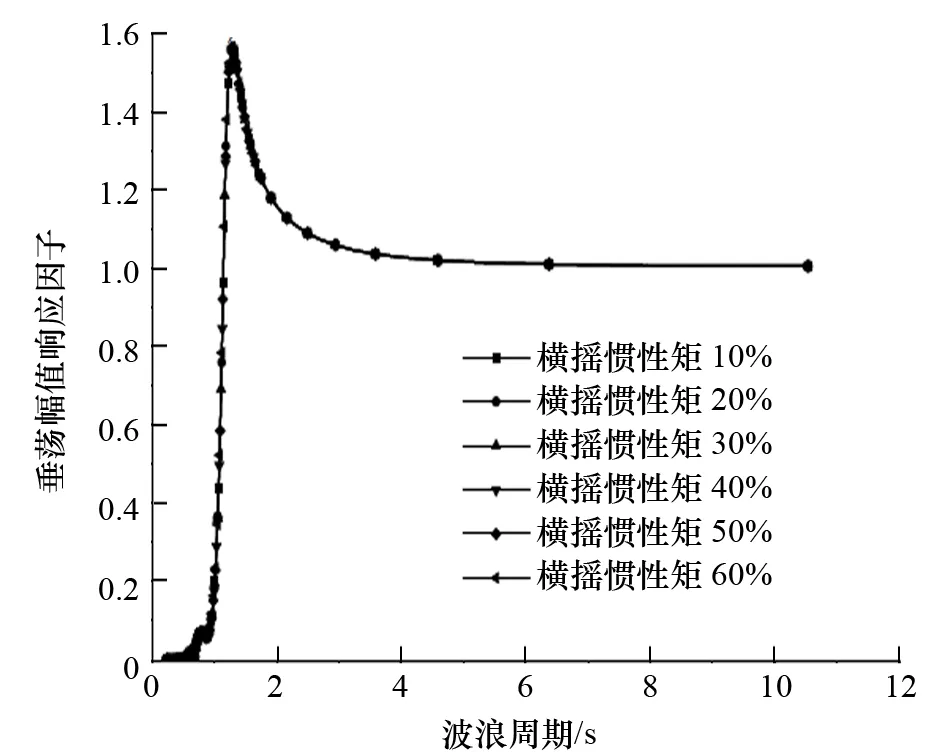
圖8 橫搖慣性矩對垂蕩運動的影響

分析圖6～圖8中各自由度的運動響應因子隨橫搖慣性矩的變化情況可以發現：

(1) 橫搖慣性矩對橫搖運動具有明顯影響。橫搖運動隨著橫搖慣性矩的增加而逐漸增大，響應幅值先向高頻再向低頻移動。

(2) 當橫搖慣性矩超過30%后，橫搖運動響應隨橫搖慣性矩增加而急劇增大。

(3) 橫搖慣性矩對無人監測船縱搖、垂蕩運動性能幾乎沒有影響。

(4) 各自由度最大幅值響應集中在周期1～2 s，已遠離渤海海浪能量集中區4.5～4.8 s。

在計算縱搖慣性矩影響的過程中保持無人監測船重心高度、橫搖慣性矩、吃水深度不變，設置k分別為10%、20%、30%、40%、50%、60%，計算結果如圖9～圖11所示。

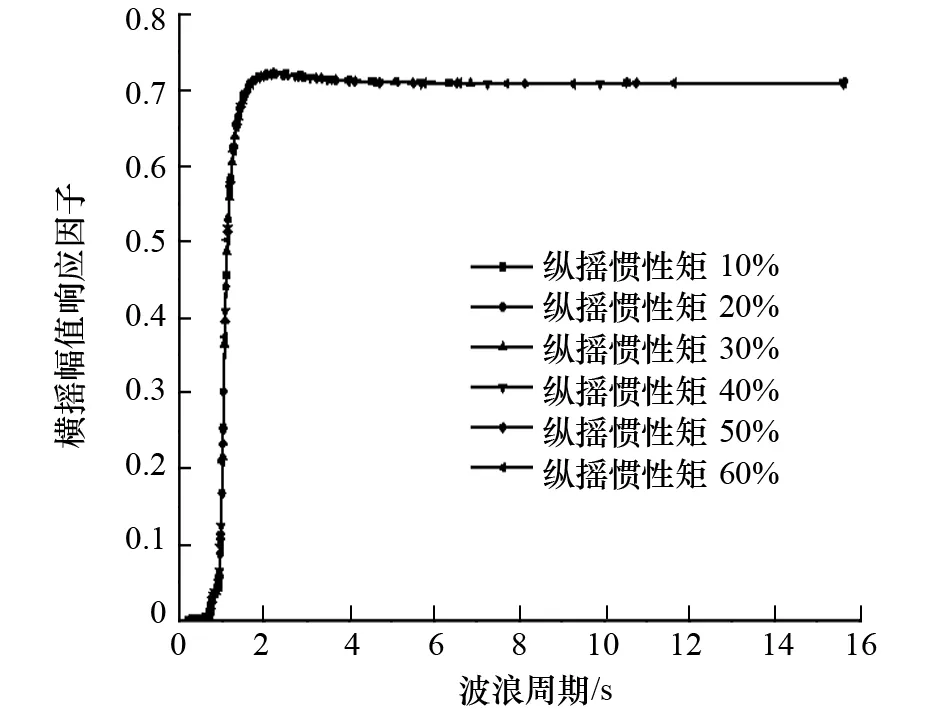
圖9 縱搖慣性矩對橫搖運動的影響

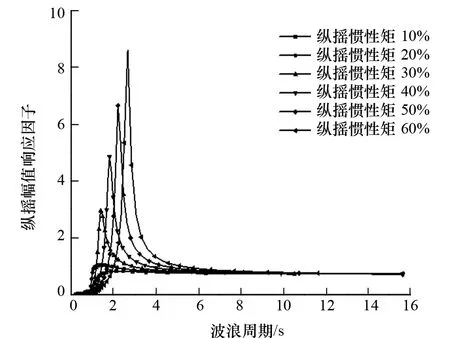
圖10 縱搖慣性矩對縱搖運動的影響

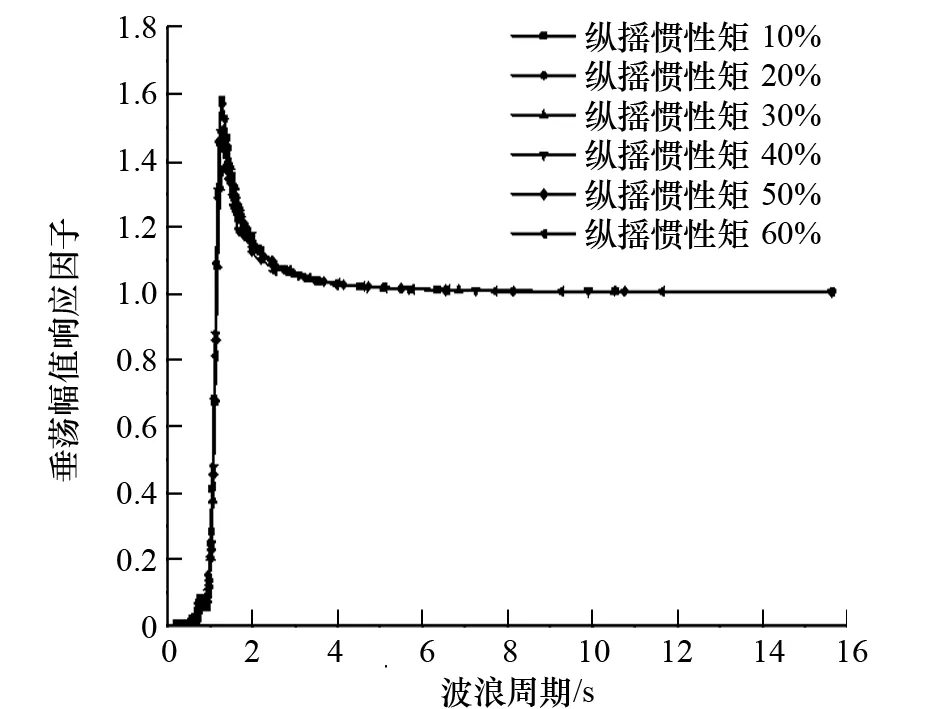
圖11 縱搖慣性矩對垂蕩運動的影響

分析圖9～圖11中各自由度的運動響應因子隨縱搖慣性矩的變化情況可以發現：

(1) 縱搖慣性矩主要影響縱搖、垂蕩的運動性能。隨著縱搖慣性矩增加，縱搖運動顯著增大，響應幅值先向高頻再向低頻移動。與此同時，隨著縱搖慣性矩增加，垂蕩運動先減小再增加，響應幅值先向低頻再向高頻移動。

(2) 縱搖慣性矩對縱搖運動的影響明顯大于對垂蕩運動的影響。

(3) 當縱搖慣性矩超過20%后，縱搖運動響應隨縱搖慣性矩的增加開始迅速增大。當達到60%以后，響應幅值對應的波浪周期與渤海波浪能量集中區較為接近，極易發生大幅度運動。

(4) 縱搖慣性矩對無人監測船橫搖運動性能沒有明顯影響。

根據上述結果，在對設備進行橫向布置時，由于橫搖慣性矩只對橫搖運動具有明顯影響，因此只需重點關注橫搖的運動響應。在通常情況下，可以考慮在一定范圍內適當增加橫搖慣性矩。在這一范圍內，無人監測船運動響應隨橫搖慣性矩增加緩慢，且幅值所對應周期逐漸減小，遠離波浪能量集中區域，有利于改善橫搖性能。在超過這一范圍后，增加無人監測船的吃水深度會使運動響應急劇增加，幅值所對應的周期向低頻移動，在渤海容易發生較大幅度的橫搖。在對設備進行縱向布置時，由于縱搖慣性矩主要影響縱搖運動，且影響幅度遠大于垂蕩運動，因此主要考慮縱搖的運動響應情況，通常應盡量將其控制在較低范圍內，避免縱搖幅值響應因子在遭遇低周期海浪時過大。

2.3 重心高度對無人監測船運動性能的影響

重心高度與無人監測船搭載儀器在垂向方向上的布置有關。分析重心高度對無人監測船運動響應的影響可在一定程度上為無人監測船搭載儀器在垂向方向上的布置方案提供依據。但需要注意的是，重心高度還是浮體穩性的重要影響參數，重心與浮心之間的高度關系會直接影響浮體的初穩性、大傾角穩性等，因此在設計過程中，重心高度的選取還應從穩性方面加以考量，使其達到穩性的要求。

在計算重心高度影響的過程中，保持無人監測船吃水深度、橫縱搖慣性矩不變。考慮到船體自身尺寸，設置重心高度分別為0.10 m、0.15 m、0.20 m、0.25 m和0.30 m。計算結果如圖12～圖14所示。

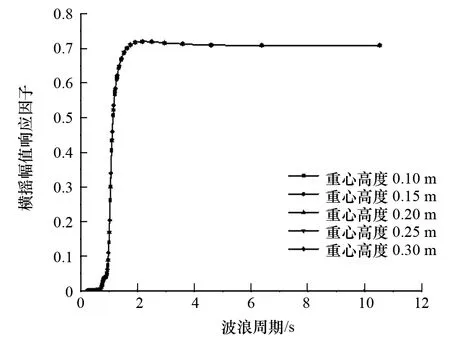
圖12 重心高度對橫搖運動的影響

圖13 重心高度對縱搖運動的影響

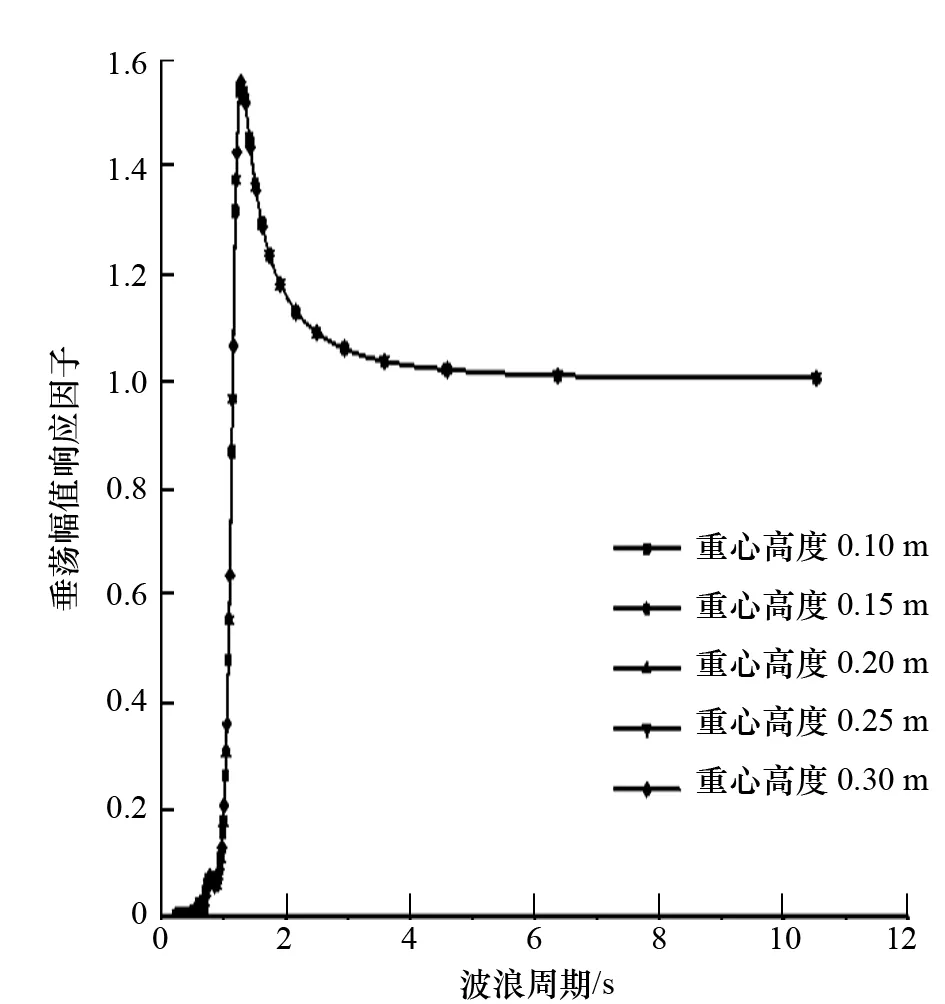
圖14 重心高度對垂蕩運動的影響

分析圖12～圖14中各自由度的運動響應因子隨重心高度的變化情況可以發現：

(1) 重心高度對3個自由度運動性能的影響均不明顯。

(2) 縱搖、垂蕩的運動響應要明顯大于橫搖的運動響應。

上述結果表明，重心高度對無人監測船的運動響應影響不大。在設計無人監測船重心高度時，應主要從穩性的角度進行考慮，使無人監測船滿足初穩性和大傾角穩性的相關要求。在通常情況下，應盡量降低重心高度，增大無人監測船的初穩心半徑。但應注意的是，重心高度不宜布置得過低，否則無人監測船搖晃運動回復速度會過快，精密儀器難以正常工作。

3 結論與展望

運用二維切片理論，計算近海小型無人監測船在不同吃水深度、橫搖慣性矩、縱搖慣性矩、重心高度等不同布置方案下在波浪中的運動響應情況，得出運動響應隨布置方案變化的規律，并以此為依據提出一系列小型無人監測船儀器設備布置原則。

由于試驗條件有限，僅運用數值計算的方法對布置方案與運動響應間的關系進行了初步的計算與分析，計算結果的準確性有待進一步通過試驗進行對比。