一種改進的MRT 預編碼方案*

姚紅艷，趙宏宇

（西南交通大學 信息科學與技術學院，四川 成都 610000）

0 引言

2010 年底，美國貝爾實驗室的科學家Marzetta T L 提出了大規模多輸入多輸出（Massive-Multiple-Input-Multiple-Output，Massive MIMO）系統時分雙工的概念[1]。該系統能大幅度增加通信系統的通信速率，提升系統的頻譜效率，但同時由于多用戶信號之間存在干擾，如何消除這些干擾成為Massive MIMO 的主要問題[2]。預編碼技術作為Massive MIMO 系統中的一項關鍵技術，可以解決多用戶Massive MIMO 的干擾問題[3]。理論上，由于基站側配置了大規模天線，所以簡單的線性預編碼即可消除用戶間干擾。最常用線性預編碼算法有最大比傳輸（Maximum Ratio Transmission，MRT）、迫零（Zero-Forcing，ZF）和正則迫零（Regularization-Zero-Forcing，RZF）預編碼算法[4-6]。其中，MRT預編碼通過對信道矩陣求共軛轉置來獲取發送預編碼矩陣，避免了矩陣求逆，計算復雜度低，易于實現，但是頻譜效率低；ZF 預編碼算法通過對信道求取廣義逆可以消除終端間干擾獲得較好的系統性能，復雜度稍高；RZF 預編碼可以取消噪聲、信道不確定性能等因素帶來的影響，獲得很好的系統性能，但是無法推導系統性能的閉式表達式。

本文將MRT 和ZF 預編碼結合，提出MRT 預編碼的改進型線性預編碼方案—Improved-MRT。在瑞利平坦衰落信道下，根據MRT 干擾信號的概率密度函數近似閉式表達式，進而分析Improved-MRT 中斷概率、中斷容量和頻譜效率。仿真結果表明，相比MRT 預編碼方案，改進的MRT 預編碼方案能夠同時服務更多的用戶而不會產生中斷，頻譜效率也更好，并且得到的各個性能閉式表達式和實際仿真結果十分接近。

符號說明：大寫粗體字母代表矩陣，小寫粗體字母代表向量，大/小寫不加粗字母代表標量，IN表示N×N的單位矩陣，|X|表示矩陣X的模值，tr(X) 表示矩陣X的跡，E[·]表示求變量期望，CN(μ，σ2)表示均值μ和方差σ2的循環對稱高斯分布，{XH，XT，X*，X-1，X+}分別表示矩陣X的共軛轉置、轉置、共軛、逆處理、廣義逆處理，表示X屬于復數平面的M×N空間上。

1 系統模型

考慮單小區多用戶Massive MIMO 系統，信道采用獨立的瑞利平坦衰落信道，信道矩陣的元素服從CN(0，1)。假設基站端知道完美的信道狀態信息（Channel State Information，CSI）。Improved-MRT預編碼矩陣為MRT 和ZF 預編碼矩陣的結合，其最終目的是在MRT 預編碼的基礎上增強期望用戶的信道增益，從而達到增加系統頻譜性能的目的，所以Improved-MRT 預編碼矩陣為：

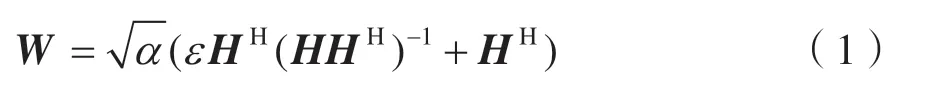
其中α為功率歸一化因子，，Pt為發射功率，為噪聲方差，代表信道矩陣，K是用戶數，M是基站（Base Station，BS）端的天線數。

經過預編碼后發射端發送信號可表示為：

其中s=[s1，s2，…，sK]T是K×1 的符號向量，sk表示k用戶的符號，且與sj(j=1，2，…，K，j≠k)獨立。每一個符號的功率歸一化為1，即滿足E[ssH]=IK。經過預編碼后的發射信號仍然需要滿足總的發射功率的限制，即為：

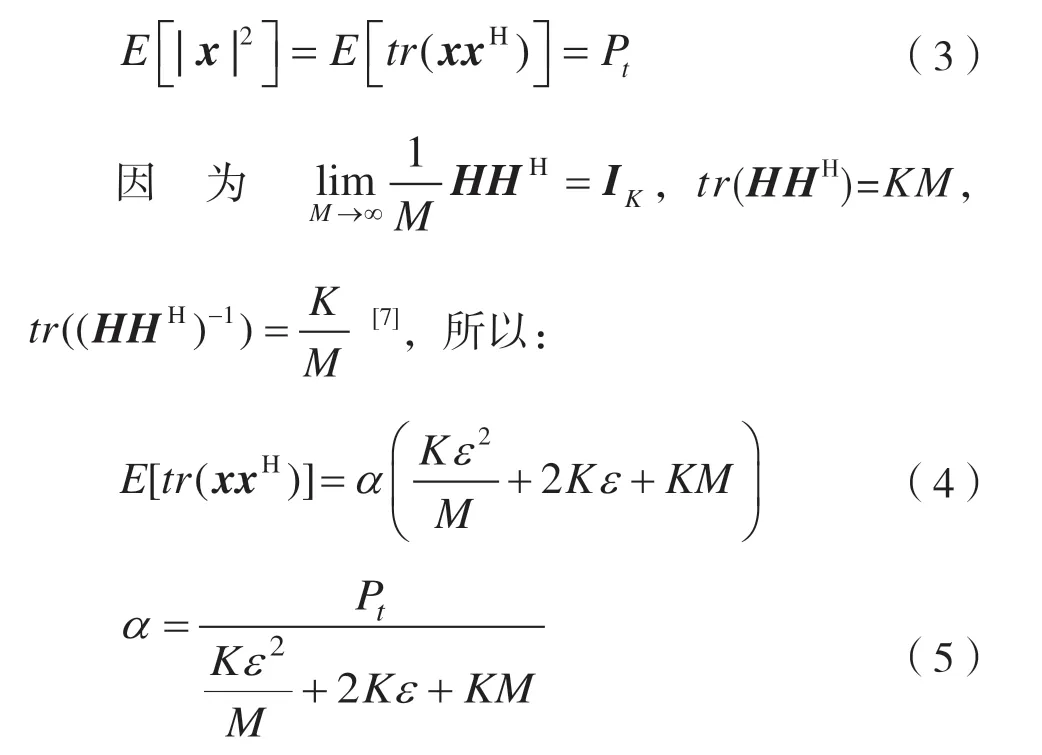
假設發送端和接收端都具有完美的CSI，那么接收信號向量為：

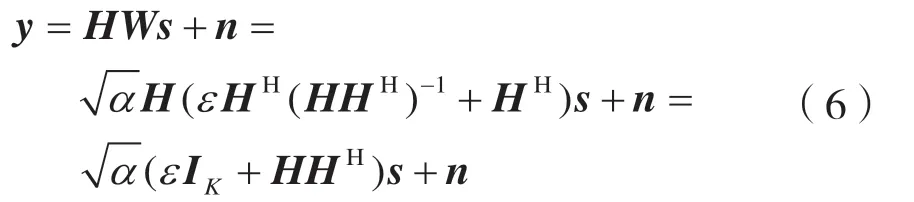
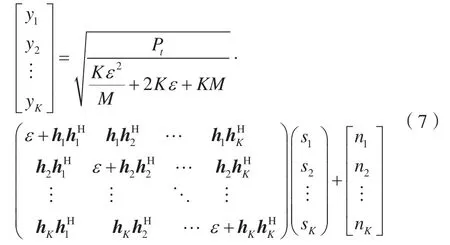
用戶k的接收信號為：

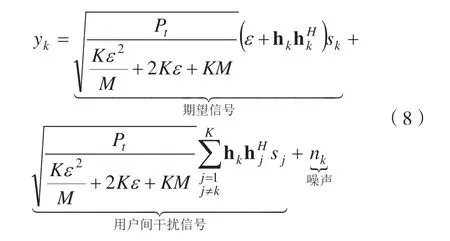
那么，用戶k的信干噪比SINR為：

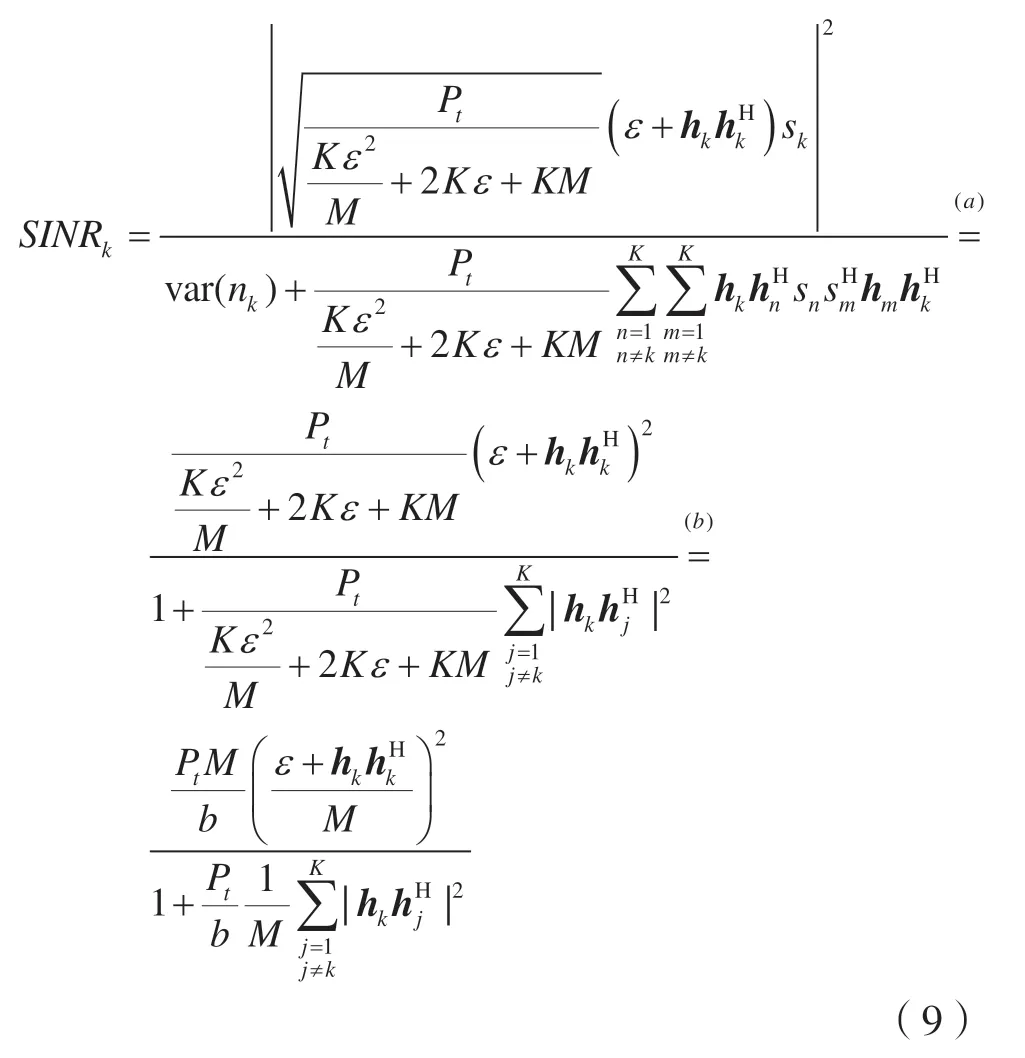
其中，（a）var(nk)表示變量nk的方差var(nk)=1，E[|sk|2]=1，(k=1，2，…，K)，E[|sksjH|]=0，k≠j；（b）

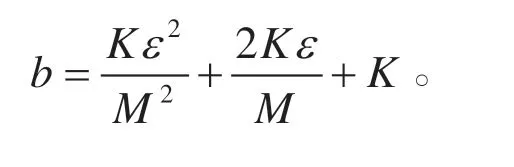
2 Improved-MRT 預編碼性能分析

在信道采用瑞利衰落信道的情況下，根據信道增益的特性得到MRT 預編碼干擾信號的概率密度函數表達式[8]，其中Improved-MRT 預編碼的干擾信號和MRT 相同。通過該表達式得到系統的頻譜效率、中斷概率和中斷容量，根據中斷概率和中斷容量評價一個系統可以同時服務的用戶數。

2.1 系統干擾信號的概率密度函數

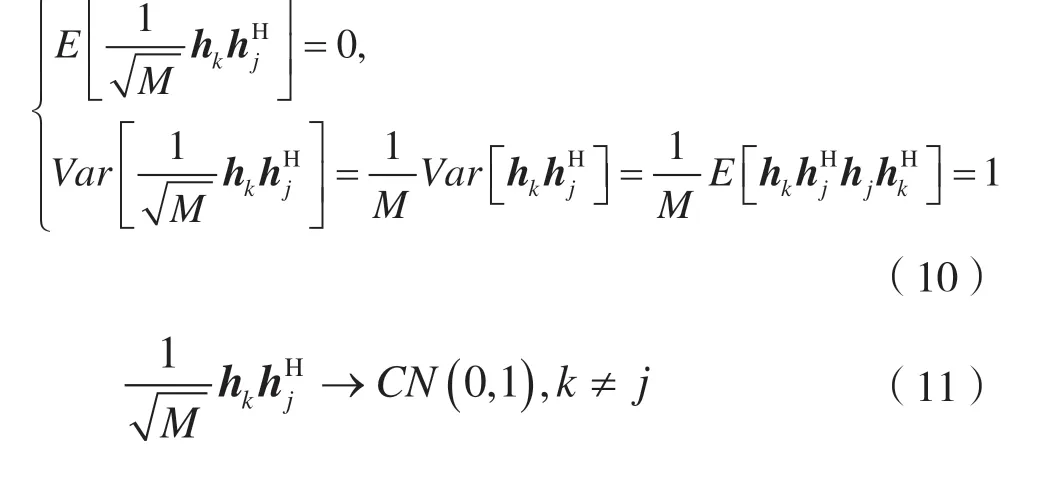
關系數為：

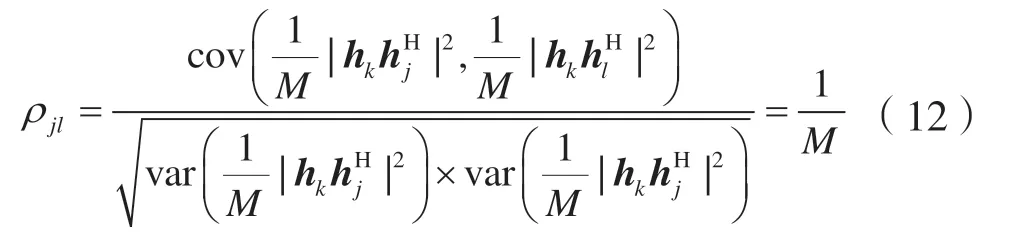
2.2 系統中斷概率分析

化簡用戶k的信干噪比為：

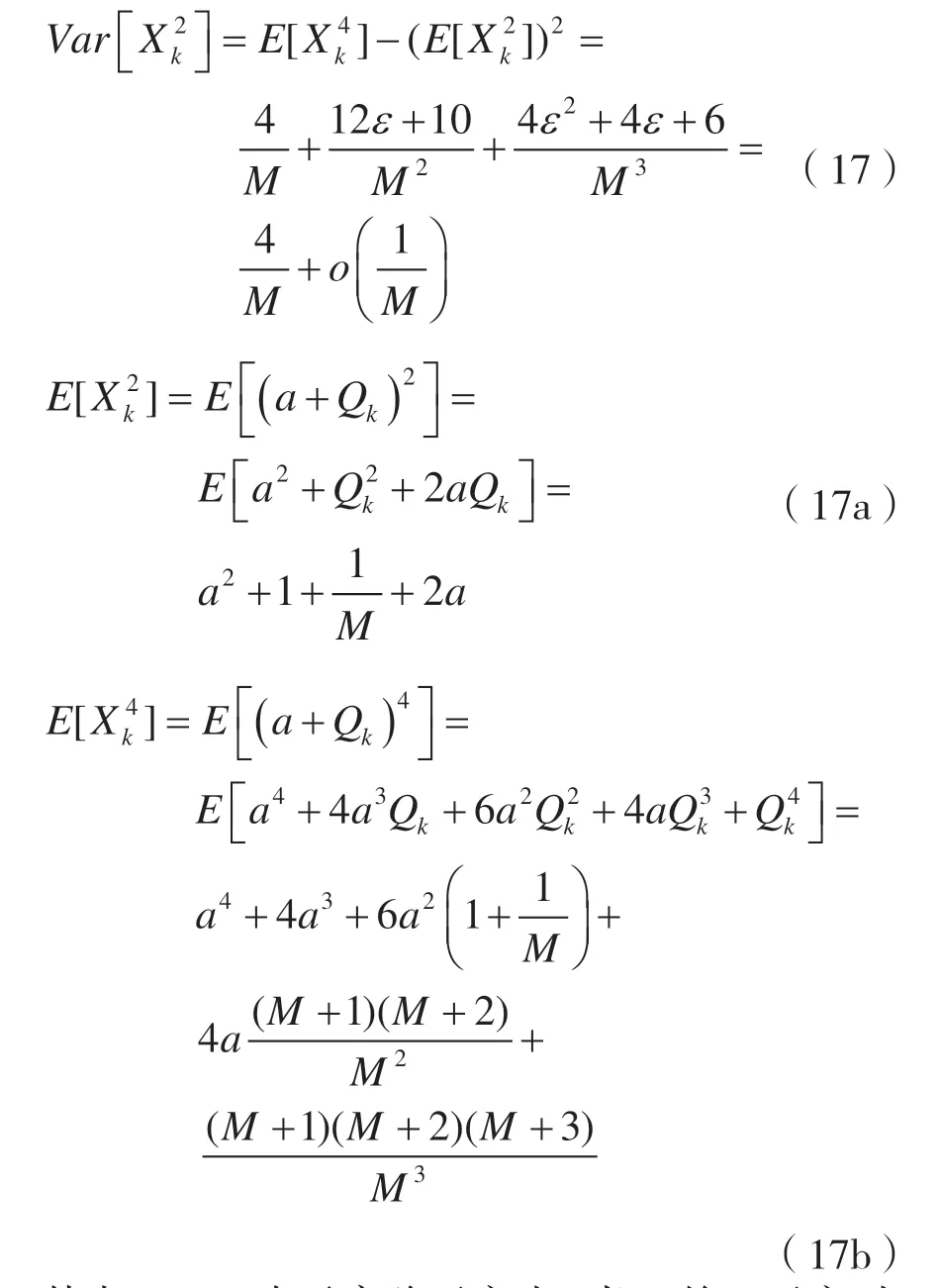
其中o(1/M)表示高階無窮小。當M趨于無窮時，只有第一項占主要的。Yk的方差可以根據其概率密度函數得var(Yk)=(K-1)(1+(K-2)/M)，那么：

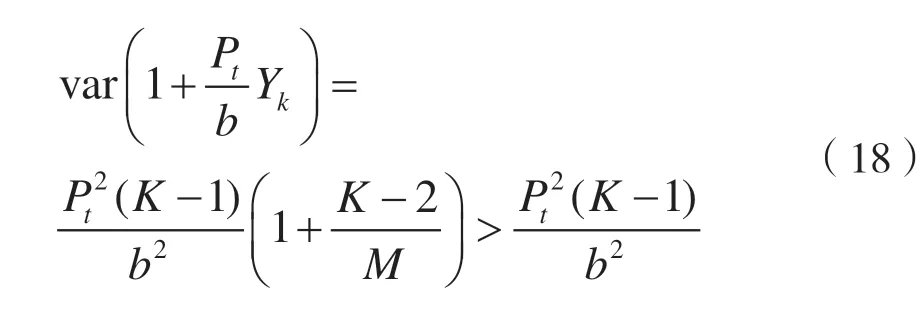
綜上所述：當M→∞時，期望信號的方差趨于0，而干擾信號的方差與Pt和b有關，所以不能忽略Pt和b。當M→∞，干擾信號的方差大于期望信號的方差，即：

可以看出，盡管傳輸的總功率很大，中斷概率也不會為0，與MRT 預編碼的中斷概率一致，得到中斷概率可以有助于設計Massive MIMO 系統期望的中斷水平，可以決定當給定rth值時大規模基站能同時服務的用戶數。

2.3 系統頻譜效率分析

當發射信號遵從高斯分布時，用戶k的頻譜效率為：

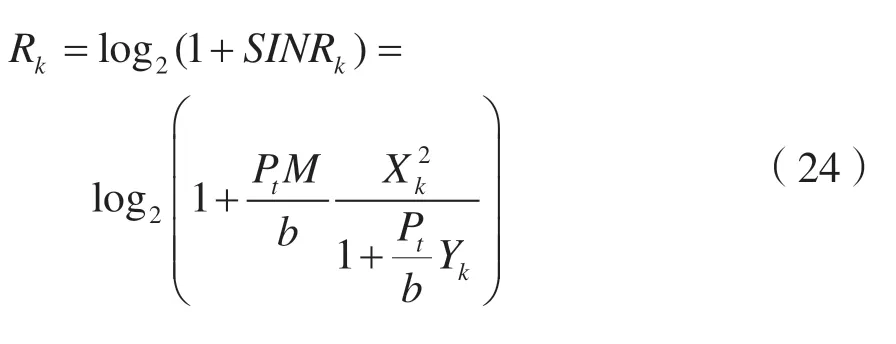
系統總的頻譜效率為所有用戶的頻譜效率之和：

2.4 系統中斷容量分析

中斷容量的定義是用戶處于非中斷狀態下的可達速率總和[12]，表達式為：

3 仿真實驗與分析

為了分析Improved-MRT 中斷概率、中斷容量和頻譜效率的閉式表達式的擬合程度，本文采用瑞利平坦衰落信道模型，信道實現取1 000 次，對Massive MIMO 系統在不同基站發射天線數、不同用戶數、不同發射功率下的性能進行全面分析，將Improved-MRT 與MRT 預編碼的性能進行比較，并且驗證本文推導出的中斷概率、中斷容量、頻譜效率的近似閉式表達式的準確性。下面分別給出這3種性能的仿真結果。

3.1 中斷概率仿真結果

圖1 是發射天線數取100 和200 時不同用戶下的中斷概率圖。當發射天線取100 中斷概率超過10%時，MRT 服務的用戶數為7 個，Improved-MRT 服務的用戶數為8 個。當發射天線數從100 增加到200 時，MRT 比Improved-MRT 服務的用戶數少4 個左右。所以，在Massive MIMO 中可以改善中斷概率主要是由于大規模天線的原因。

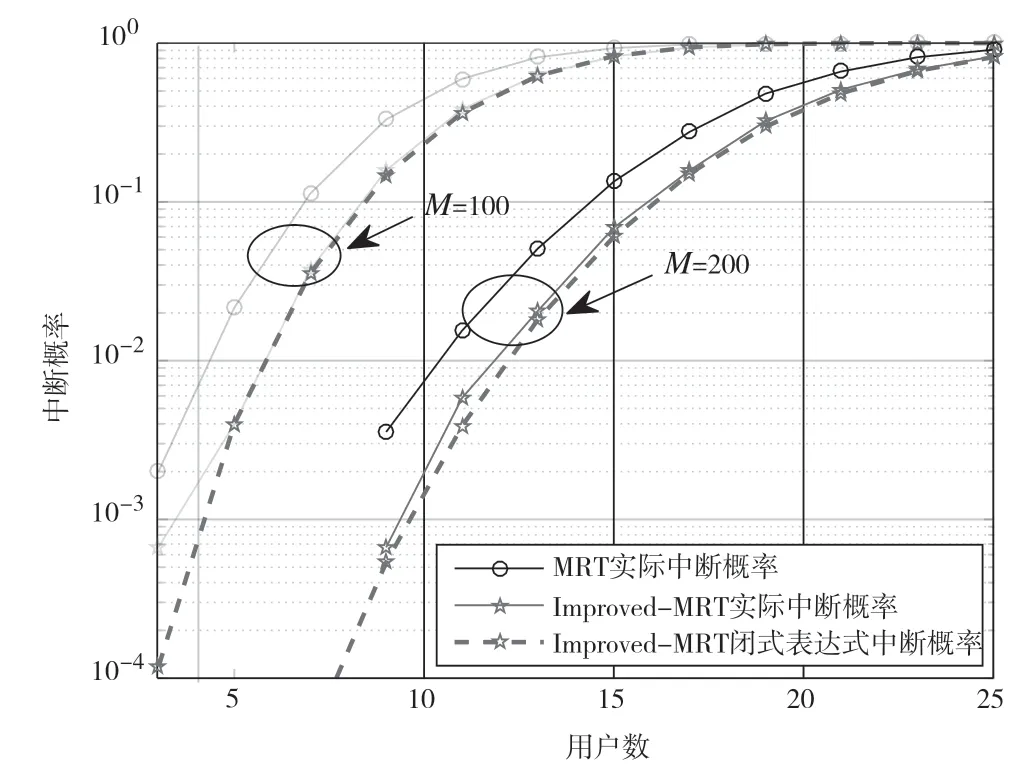
圖1 Pt=10 dB，rth=10 dB 不同用戶的中斷概率

圖2 為基站配備不同天線的中斷概率圖。可以看出，M很小的時候，閉式表達式也能很好地接近真實的仿真圖像。當總的發射功率為10 dB 時，Improved-MRT 需要120 根天線來達到10%的中斷概率，而MRT 需要140 根天線才能達到同樣的性能。當發射功率減少到7 dB 時，Improved-MRT 需要增加20 根天線就能達到同樣的性能，MRT 僅僅增加10 根天線就能達到同樣的性能。對于MRT 來說，改變總的發射功率，Massive MIMO 的中斷概率沒有特別明顯的差異。

圖3 是不同發射功率的中斷概率圖。隨著總的發射功率的增加，系統的中斷概率也不會趨于0，主要是由于MRT 和Improved-MRT 沒有完全消除用戶間干擾，但是Improved-MRT 隨著總的發射功率的增加比MRT 的中斷概率衰減得更快，主要是由于Improved-MRT 的期望用戶的增益大，抑制干擾能力更強。當發射天線數為100 時，總的發射功率為15 dB，MRT 的中斷概率為0.3，Improved-MRT的中斷概率為0.05，所以Improved-MRT 的中斷概率優于MRT。隨著天線數增加到150，MRT 的中斷概率保持到低于0.1 僅僅需要的發射功率為8 dB，Improved-MRT 的中斷概率保持到低于0.1 需要M=100 的發射功率為13 dB 或者M=150 的發射功率為6 dB。可見，大規模的天線數比增加發射功率改變中斷概率的性能更加明顯。

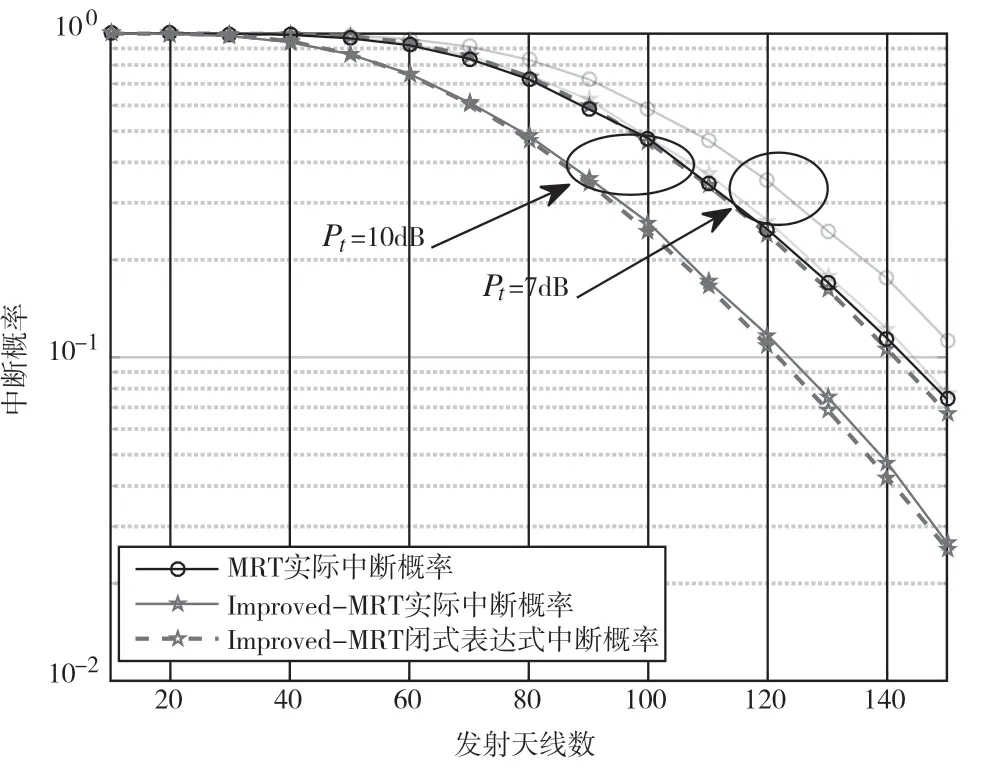
圖2 K=10，rth=10 dB 不同發射天線中斷概率

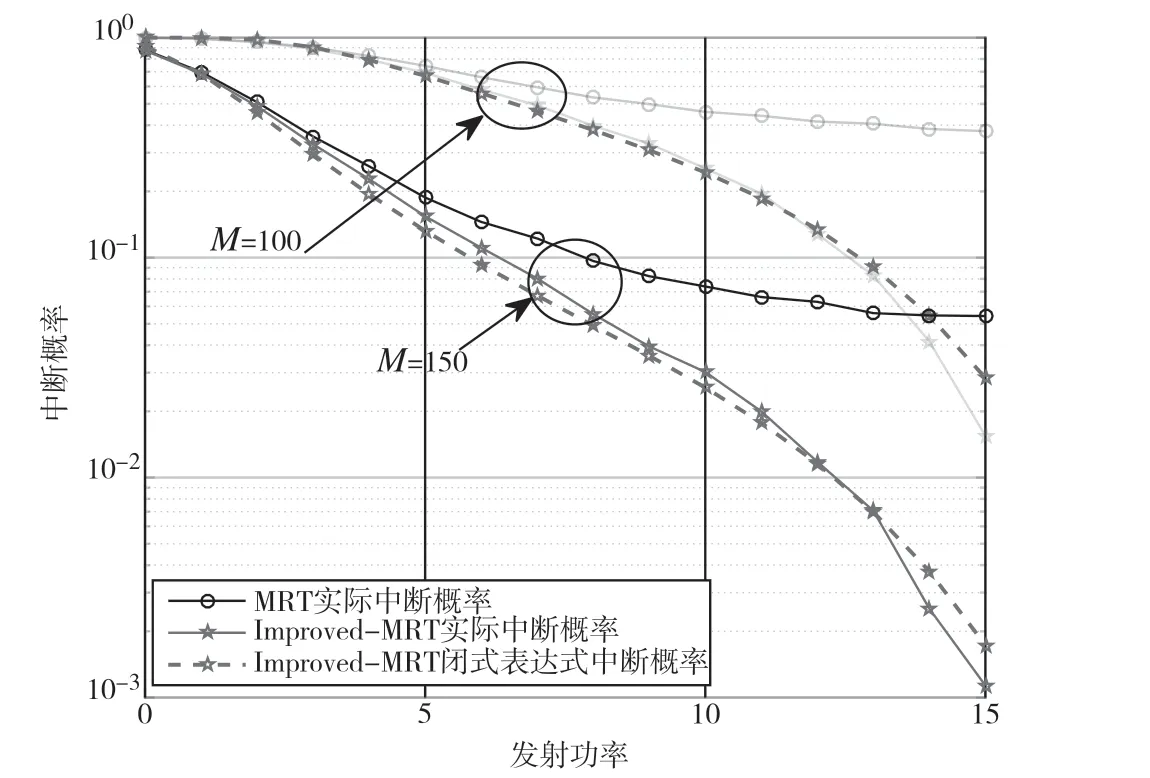
圖3 K=10，rth=10 dB 不同發射功率的中斷概率

3.2 頻譜效率仿真

圖4 顯示了高信噪比情況下隨著用戶數的增加，系統的頻譜效率增加。可以看出，MRT 預編碼的頻譜效率略低于Improved-MRT 預編碼，且閉式表達式和實際的仿真結果十分接近，但是兩者的頻譜效率遠低于ZF 預編碼。究其原因，主要是ZF 預編碼是假設完全抑制干擾的情況下得到的，這在實際信道中很難達到。

圖4 高信噪比情況下不同用戶的頻譜效率

圖5 為低信噪比情況下隨著用戶數的增加，MRT 和Improved-MRT 預編碼的頻譜效率不斷增加。當用戶數在5～25 之間時，ZF 預編碼的頻譜效率也是增加的；用戶數在25～40 之間時，頻譜效率逐漸下降，主要是由于ZF 預編碼并未考慮噪聲的影響，在低信噪比情況下，信道噪聲占主要影響。當用戶數較少時，系統可以保持較好的頻譜效率。隨著用戶的增加，由于ZF 預編碼用戶數量過多會造成輸出SINR 的嚴重下降，使得系統的頻譜效率嚴重下降。

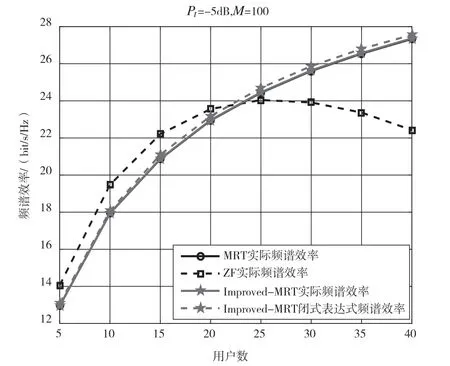
圖5 低信噪比情況下不同用戶的頻譜效率

3.3 中斷容量仿真

圖6 為不同用戶下的中斷容量圖。在很少用戶數的情況下，隨著用戶的增加或者閾值的減少，中斷容量增加。對于閾值取7 dB 時，Improved-MRT的用戶數達到16 時中斷容量開始下降，當用戶數達到36 時，中斷容量趨于0，所有用戶處于中斷狀態；MRT 的用戶數達到14 時中斷容量開始下降，當用戶數達到32 時，中斷容量趨于0，所有用戶處于中斷狀態。該圖顯示了中斷概率的重要性。隨著用戶數K的增加，理論上總的頻譜效率應該增加，但更多的用戶會處于中斷狀態，所以實際系統的通吐量將會降低。

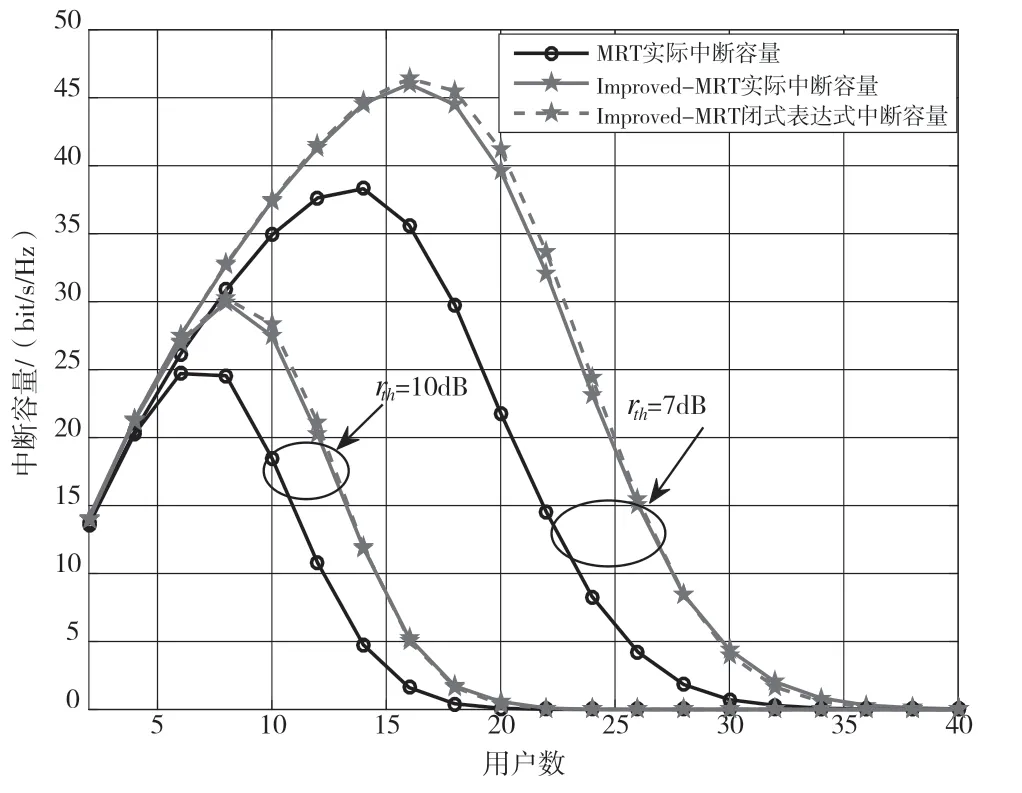
圖6 Pt=10 dB，M=100 不同用戶的中斷容量

4 結語

本文根據MRT 預編碼和ZF 預編碼，提出了一種改進的MRT 預編碼方法。該方法主要是在MRT預編碼的基礎上增強期望信號的信道增益，同時干擾和MRT 預編碼的干擾大小一樣，并且假設發射天線數很大或者趨于無窮，服務的用戶數偏中等，根據中心極限定理，在瑞利平坦衰落信道中分析了該預編碼的干擾功率，得到了干擾功率的概率密度函數的近似閉式表達式。通過比較信號功率和干擾功率的方差，將信號功率用其均值代替。干擾功率作為一個隨機變量進行分析，得到了系統的頻譜效率、中斷概率和中斷容量的閉式表達式，然后與理論仿真結果進行對比驗證，可以得到閉式表達式，從而能夠很好地擬合實際系統的性能。

隨著用戶數的增加，中斷概率和中斷容量的性能越來越差。所以，根據中斷容量可以知道每個系統最多服務的用戶數。由于Improved-MRT 是在MRT 基礎上的改進，其性能比MRT 性能好，同時服務的用戶數更多，中斷概率更小，但是復雜度會有一定的提升，主要涉及到矩陣的求逆。針對矩陣求逆可以采用文獻[13]中迭代的方法進行求解，使系統的復雜度減少。所以，總體來說，Improved-MRT 預編碼的性能要優于MRT 預編碼。