構造多維阿基米德Copula生成元的方法

(蘭州交通大學數理學院 甘肅 蘭州 730000)

一、引言

阿基米德Copula作為Copula函數類的一種特殊Copula，阿基米德Copula由于構造方便、計算簡單，且有很多良好的性質在許多領域尤其是金融領域得到了廣泛應用.目前對于阿基米德Copula的研究已經有了很多成果，阿基米德Copula是由生成元構成的copula，生成元是一種單調遞減的凸函數.有了生成元就可以構造出阿基米德Copula.文獻[3]中提出了構造阿基米德Copula生成元的常見方法：拉普拉斯變換法.之后在文獻[6]中提出了利用可導的條件構造生成元的方法，在文獻[7]中對于阿基米德Copula的生成方法也從加法推廣到乘法，文獻[4]則將構造方法不再局限于概率密度函數而是拓展到實數范圍.李霞將這些對于阿基米德Copula的研究成果都編繪進文獻[5]中，基于以上研究，本文由單一參數推廣到多參數構造生成元的方法進行了研究，提出了多維阿基米德Copula生成元的構造方法.

二、預備知識

(一)阿基米德Copula函數定義

定義1[2]：設φ是[0,1]→[0,∞]上的連續的、嚴格降的凸函數，且φ(1)=0，則φ的偽逆φ[-1]是[0,∞]→[0,1]上的函數，且

則具有C(u,v)=φ[-1](φ(u)+φ(v))形式的Copula稱為阿基米德Copula，φ稱為Copula函數的生成元.如果φ(0)=∞，則稱φ為嚴格的生成元.此時，φ[-1]=φ-1，C(u,v)=φ-1(φ(u)+φ(v))稱為嚴格的阿基米德Copula函數.

(二)阿基米德Copula生成元的常用構造方法

三、二維阿基米德Copula生成元的構造方法

目前對于構造阿基米德Copula生成元主要從變換和函數角度進行研究，本文將從維數角度去考慮構造生成元，首先討論在二維的條件下構造阿基米德Copula生成元.

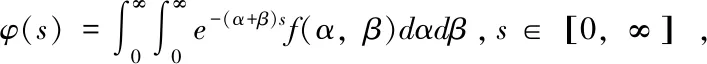
證明：若要驗證φ-1(s)為阿基米德Copula生成元，需要φ-1(s)滿足阿基米德Copula生成元的幾個條件，其中需要φ-1(1)=0，φ-1(s)是連續的、嚴格遞減、凸函數.

(2)φ(s)由表達式顯然連續，則φ-1(s)也連續；

(4)已知φ-1為凸函數當且僅當φ為凸函數，所以只需證明φ為凸函數.

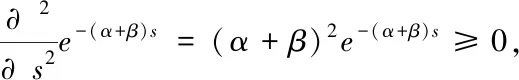
由上可知φ(s)是凸函數，則φ-1(s)為凸函數，又因為φ(∞)=0，則φ-1(0)=∞，即可證明φ-1(s)是一個嚴格的阿基米德Copula的生成元.

例1：設二維獨立隨機變量(α,β)具有密度函數f(α,β)=e-(α+β)，其中α,β≥0，則對密度函數進行拉普拉斯變換

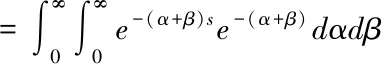
以上被積函數中的f(α,β)是密度函數，比較特殊，當f(α,β)不再是密度函數而是定義在R+×R+上非負連續函數時，以下定理能被得出.

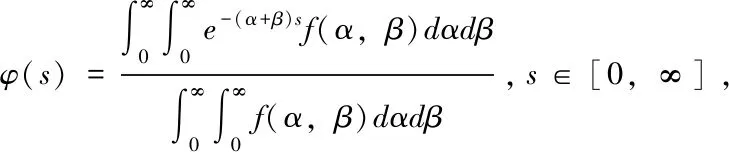
證明：此定理的證明和定理1的證明步驟相同，則著重證明φ-1為凸函數.

由上已知φ-1為凸函數當且僅當φ為凸函數，所以只需證明φ為凸函數.

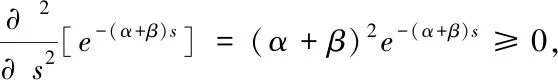
所以φ(s)是凸函數，則φ-1(s)為凸函數，又因為φ(∞)=0，則φ-1(0)=∞，即可證明φ-1(s)是一個嚴格的阿基米德Copula的生成元.

四、多維阿基米德Copula生成元的構造方法

通過討論二維阿基米德Copula生成元的構造方法，我們可以推廣到多維上來構造生成元，這樣擴大了阿基米德Copula生成元的生成條件，有利于阿基米德Copula函數的應用在實際中.下面給出了多維非負連續函數構造生成元的方法.

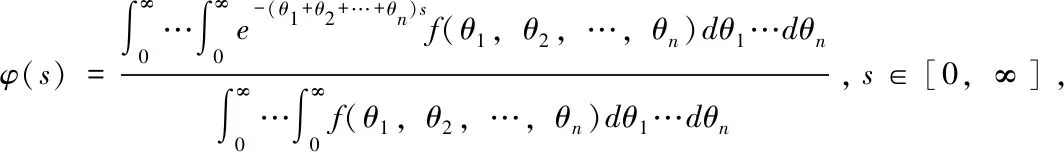
證明：

(2)φ(s)由表達式顯然連續，則φ-1(s)也連續；

(3)φ′(s)=

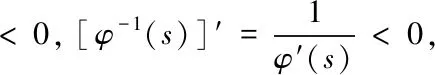
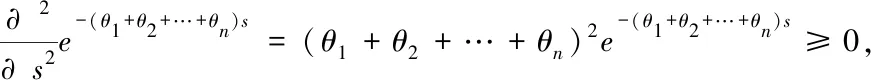
e-(θ1+θ2+…+θn)[λs1+(1-λ)s2]≤λe-(θ1+θ2+…+θn)s1+(1-λ)e-(θ1+θ2+…+θn)s2

則

所以φ(s)是凸函數，則φ-1(s)為凸函數，又因為φ(∞)=0，則φ-1(0)=∞，即可證明φ-1(s)是一個嚴格的阿基米德Copula的生成元.

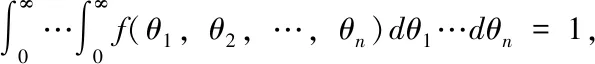
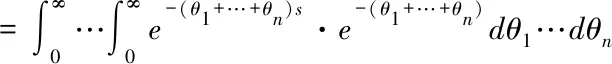
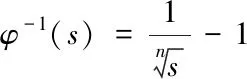
這樣可以和例1結合得到如下多維阿基米德Copula函數

五、小結

阿基米德Copula函數在模型選擇，建立數據之間的簡單聯系有著重要的作用.本文基于前人研究基礎上擴大了求取生成元的條件，不再局限于嚴格單減的凸函數和一維函數，但是還有待研究對于隨機變量是不獨立的情況下構造生成元這一難題.