關(guān)于哥德巴赫猜想

西北工業(yè)大學(xué)附中 李一霖

一、準(zhǔn)備：(字母均表示正整數(shù))

“一切大于等于6 的偶數(shù)，均可表示為兩個質(zhì)數(shù)的和‘等價于’一切大于等于3 的質(zhì)數(shù)，可以表示大于等于6 的全體偶數(shù)”。以下給出幾個定義及性質(zhì)定理：

定義：在質(zhì)數(shù)集中(設(shè)質(zhì)數(shù)為an，n為質(zhì)數(shù)編號，恒有an＜an+1)，將{ai}(i∈[1，n])稱為n個已知質(zhì)數(shù)，已知質(zhì)數(shù)從質(zhì)數(shù)列由小到大順次取得(如已知2、3、5 時，{ai}增加一項只可為7)，這n個質(zhì)數(shù)各自倍數(shù)集的并集A在N＊中補集稱為n階已知質(zhì)數(shù)列，記為{xn}，其中n為階數(shù)，也為已知質(zhì)數(shù)數(shù)量。

二、n 階已知質(zhì)數(shù)列的性質(zhì)

1.{xi}中xi+1-xi的值是循環(huán)的，循環(huán)節(jié)長度(即第m個循環(huán)節(jié)首項與第m+1 循環(huán)節(jié)首項差之絕對值)為an的階乘。

證明：由互質(zhì)知，設(shè){ai}所有項最小公倍數(shù)為bn=an！，{ai}各項倍數(shù)集都包含kbn(kN＊)，n個倍數(shù)集均出現(xiàn)的數(shù)是且僅是bn的倍數(shù)集。對{xn}中任一項xi(i表示項的序數(shù))，由最小公倍數(shù)為bn，每項xi+mbn必然也在該數(shù)列中，故{xn}每個以bn為長度的循環(huán)節(jié)內(nèi)遞增速度循環(huán)，n一定時，循環(huán)節(jié)固定。

2.n階已知質(zhì)數(shù)列中一項xi必然為真實質(zhì)數(shù)(在正整數(shù)集中恰有兩因數(shù)，即確實為質(zhì)數(shù))的充分條件是xi＜an2(an為{ai}中最大一項)。證明：設(shè){xn}中任一項xi＜an2，分解因數(shù)得xi=p1p2……pr，(r≥2)，其中pi為質(zhì)數(shù)且pi≥an，則m≥an2，這與m＜an2矛盾。故xi分解所得至少有一項pi≤an，則這樣的xi應(yīng)已被篩除，故任一項xi＜an2均不可質(zhì)因數(shù)分解。故{xi}中取任一項xi＜an2，xi為真實質(zhì)數(shù)。

3.n階已知質(zhì)數(shù)列在n遞增時，逐漸篩除已知質(zhì)數(shù)列各項。新增已知質(zhì)數(shù)an+1，只可能篩除xi＞an2，由質(zhì)因數(shù)分解得數(shù)項存在某一項pi≥an可得該性質(zhì)。

4.定義{xn}在第m區(qū)間中的任一項滿足xi∈( ， )。當(dāng)n遞增至正無窮，{xn}將趨向真實質(zhì)數(shù)列。由上知，新增已知質(zhì)數(shù)an+1能確定第n區(qū)間的真實質(zhì)數(shù)，第n-m區(qū)間(m≥1)真實質(zhì)數(shù)已由ai(i≤n)確定。

三、真實質(zhì)數(shù)列與兩項差數(shù)列

定義：設(shè){xn}中兩鄰項xi+1、xi(i∈N＊)，取全部yi=xi+1-xi，yi由y1始順次排列稱n階兩項差數(shù)列，記為{yn}，n為階數(shù)。

注：{xn}在m區(qū)間內(nèi)所有項對應(yīng)所得的{yn}，稱為第m區(qū)間內(nèi)的{yn}。將第二部分中的性質(zhì)推廣到{yn}：易知{y1}中yi=2，{y2}中有y2i-1=2，y2i=4，n給定時，{yn}各項固定，且n遞增時對{xn}篩除xi，使得xi在{yn}中對應(yīng)的前后兩項yi與yi+1相合為一項yi+yi+1。由上可知n給定時，設(shè){yn}的固定循環(huán)節(jié)為Yn，且n增大時{xn}中所有項xi(滿足xi＞an2)對應(yīng)的yi某些對鄰項相合，使得其遵循循環(huán)Yn+1，且不會對xi(滿足xi＜an2)對應(yīng)的任一yi產(chǎn)生影響。

定義：k個已知質(zhì)數(shù)順次增加t個，導(dǎo)致第m區(qū)間內(nèi)，{yk}升階為{yk+t}，導(dǎo)致某些鄰項相合為一項，稱為t次相合。

相合性質(zhì)：①在m區(qū)間內(nèi)對{yk}進行t次相合，所得{yk+t}所有項之和不變，即{yk}與{yk+t}在第m區(qū)間內(nèi)所有項和相同。

證明：設(shè){yk}與{xk}中任一項yi=xi+1-xi，設(shè){ai}中新增ak+1，即相合一次。

當(dāng)m≤k-1 時，第m區(qū)間中，{xk}中任意xi＜ak2，由上，ak+1不會對{xk}及{yk}造成影響，即相合前后第m區(qū)間內(nèi){yk}所有項和相同，所有項均不變。

當(dāng)m≥k時，第m區(qū)間中{xk}滿足任意xi＞ak2，設(shè){xk}中有xi+n數(shù)項(n為定值且n≥1)，對應(yīng){yk}中yi+n數(shù)項。由上性質(zhì)，若ak+1篩除xi+t(t∈[2，n-1])得到xi+1、xi+n，相應(yīng)地，{yk}中各項yi+n相合為yi+1+yi+2…+yi+n一項，即此時僅有{yk}所有項相同。相合1 次可遞推至t次。

定義：展開是相合的逆向變形，在第m區(qū)間中k個已知質(zhì)數(shù)由大到小減少t個，每次減去最大一項，使得{yk}降階為{yk-t}，稱為對{yk}t次展開。

展開與相合證明同理，其性質(zhì)為：對第m區(qū)間內(nèi){yk}t次展開，所得{yk-t}在該區(qū)間內(nèi)各項和不變，m≤k-t-1 時，各項相同，m≥k-t時，部分項各自展開為和不變的一列順次排列的項，代替原數(shù)位置。

兩項差數(shù)列及其循環(huán)節(jié)的性質(zhì)：由{yk}升階為{yk+1}，循環(huán)節(jié)長度變?yōu)樵镜腶k+1倍，其性質(zhì)如下：①記{yk}循環(huán)節(jié)為Yk，由上，Yk+1為Yk重復(fù)ak+1次并對某些項相合所得，且Yk+1中相鄰兩個Yk中相合的兩項在各自所在Yk中所處位置不同(yi到自身所在的循環(huán)節(jié)Yk首項間所有項之和看作yi在循環(huán)Yk中的位置)。

證明：設(shè){xk}循環(huán)節(jié)長度為bk=ak！，又設(shè){xk}與{yk}中yi=xi+1-xi，當(dāng){xk}升一階，{ai}中新增ak+1使得xi被篩除，使得{yk}中yi-1與yi相合。由Yk長度為bk，故{xk}中，xi在下一個循環(huán)節(jié)相同位置的數(shù)為xi+bk(xi丨ak+1)，由bk與ak+1互質(zhì)，又ak+1丨xi，故xi被篩除時，xi+bk不被篩除。經(jīng)遞推，其對t次相合同樣適用。

四、等價命題證明

定義：從{xn}中選取一個固定的數(shù)q，稱為基數(shù)，q順次加上{xn}所有項，所得數(shù)列稱為基數(shù)x的n階基數(shù)和列，記為{zn}=q+{xn}。

由數(shù)學(xué)歸納法：當(dāng){an}中n=1 時，{x1}中任一項xi=2i-1，{yi}中任一項yi=2。取{x1}中3 為q1，q1+{x1}=2i+2，又i∈N＊，故{x1}中取兩數(shù)可表示一切質(zhì)數(shù)ai(ai≥6)，但所取兩數(shù)不一定均為質(zhì)數(shù)。

當(dāng){an} 中n=2 時，{x2} 任 一 項x2i-1=6i-5，x2i=6i-1，{y2} 任 一項y2i-1=4，y2i=2， 以3 為q1，q1+{x2} 中z2i-1=6i-2，z2i=6i+2. 與正偶數(shù)列相比，6i+4 未表示，更換基數(shù)q2=5，q2+{xn}為z2i-1=6i，z2i=6i+4，則6i+4 得到表示，則在{x2}中取兩項求和可表示6 以上全體偶數(shù)。

故若能證明“在已知質(zhì)數(shù)篩除過程中，基數(shù)q的m階基數(shù)和列中每一個篩除的偶數(shù)均可通過更換基數(shù)得到表示”，則“一切大于等于3 的質(zhì)數(shù)，可以表示大于等于6 的全體偶數(shù)”。下述證明過程通過圖形理解為(下行為上行鄰項差)：

{xk}：q3→q3+d…xi+1-d←xi+1、xi+2、xi+3

{yk}：…d………………d、yi+1、yi+2

證明如下：設(shè)yi=xi+1-xi，對于給定的k，設(shè){xk} 中有三項xi+m(m∈[1，3])，在{yk} 中 對 應(yīng) 兩 項yi+m(m∈[1，2])，當(dāng){ai} 中新增ak+1，使得xi+2被篩除，則升階前基數(shù)q3與xi+2相加所得偶數(shù)xi+2+q3，升階后xi+2+q3無法表示，不妨設(shè)xi+2≥q3。在{xk}中，取整數(shù)d，使得xi+2-d也在{xk}中，對應(yīng)地，{yk}中取得順次相鄰數(shù)項yi+n(n≤1)其和也為d，將和為d的這部分項yi+n記為A。記q3位于第r-1區(qū)間，是{xr}的一項。將A在和為d不變時，經(jīng)過k-r次展開得{yr}相同位置的對應(yīng)部分D，可能有部分項各自拆分為兩鄰項。D是Yr的一部分，與{yr}中每個循環(huán)節(jié)相同位置的數(shù)項完全重合，由此可在D不變的前提下轉(zhuǎn)移D在{yr}中所在的循環(huán)節(jié)，但在各自循環(huán)節(jié)中位置固定。設(shè)D首項為s，轉(zhuǎn)移D在{yr}中所在的循環(huán)節(jié)，使q3與q3在{xr}中下一項之差為s，即使得在{xr}中q3對應(yīng){yr}中的s。這一過程可行性后文論證。用q3順次加上D的所有項，可知q3+d存在于{xr}。故q3+d在{xr}中，xi+2-d在{xk}中，由xi+2≥q3，q3所在區(qū)間不高于xi+2所在區(qū)間，由性質(zhì)知r與k充分大時，存在d使得q3+d、xi+2-d均在{xk}中，即從{xk}中，取q3+d、xi+2-d相加可得偶數(shù)ak+1+x。k增大時，重復(fù)執(zhí)行該過程，使得由篩除而無法表示的偶數(shù)得到表示。

論證以上內(nèi)容中的q必然可以取到，如下：對于給定基數(shù)q，{xk}升一階后篩除的質(zhì)數(shù)ai+2，不妨設(shè)x≤ai+2，設(shè)q位于第r-1 區(qū)間，是{xr}中一項，設(shè){yr}循環(huán)節(jié)為Yr，有r≤k。如下圖，一個Yr循環(huán)用相鄰兩條“丨”之間所有項表示，將{yr}升階為{yk}，由相合性質(zhì)得相鄰兩豎線間的各項和相等，故設(shè)n表示各自所在循環(huán)節(jié)的第n項，且規(guī)定：若n項前有鄰項相合，該項的序號n不變，即項數(shù)相同時，該項所在循環(huán)節(jié)中該項前所有項和相同，即位置相同。nm表示第m個循環(huán)的第n項。下圖每兩行為一橫行，一行為{yr}，第二行為對應(yīng)的{xk+1}，↓下方為箭頭左右兩項之差。

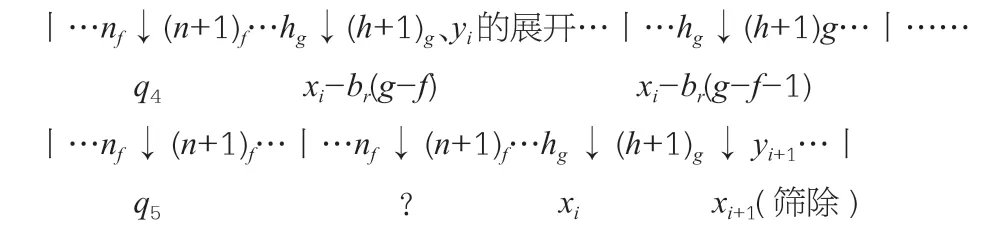
設(shè)循環(huán)節(jié)長度為br=ar！，設(shè)圖中首個循環(huán)節(jié)為第f個，末尾為第g個。第g個循環(huán)節(jié)中hg、(h+1)g兩項在第f個循環(huán)節(jié)中可找到相同位置完全相同兩項，或相鄰三項(或以上)可相合后變?yōu)閔g、(h+1)g兩項，故將hg、(h+1)g轉(zhuǎn)移至第f個循環(huán)中，得到相同位置兩項或以上的相合.不妨設(shè)所得項在nf、(n+1)f后方，如圖所示，其對應(yīng){xk+1}中項為ak-br(g-f)，若取△1=xi-br(g-f)-q4，△代表{yr}中q4至xibr(g-f)所有項之和，將△1轉(zhuǎn)移至第g個循環(huán)中從(h+1)g向前排列，且由相合性質(zhì)可保證在和不變時(項可能相合)但項數(shù)均不變，在第g個循環(huán)中，△1排列得nf.(n+1)f.但由于f到g所在區(qū)間提高，新增質(zhì)數(shù)可能導(dǎo)致？處質(zhì)數(shù)被篩除，需討論：①nf、(n+1)f之間的質(zhì)數(shù)未被篩除，則△1作為③中的d，xi-br(g-f)作為新基數(shù)，？處的質(zhì)數(shù)與新基數(shù)相加，最終表示篩除的偶數(shù)xi+q4。②nf、(n+1)f之間質(zhì)數(shù)被篩除，則將hg、(h+1)g轉(zhuǎn)移到第f+1 個循環(huán)，如圖，同理得△2，將△2轉(zhuǎn)移至g與g-1 個循環(huán)節(jié)中，若第g個循環(huán)節(jié)中？處質(zhì)數(shù)被篩除，則第g-1 個循環(huán)節(jié)中，相同位置兩項nf、(n+1)f不會進行相合，則此時q5必存在于{xk+1}中，可見③中d必然可以取到。

綜上，由數(shù)學(xué)歸納法得“在{ai}中項增多，即{xn}被篩除過程中，{zn}中每個被篩除的偶數(shù)均可通過更換q表示”，即有“一切大于等于3兩個的質(zhì)數(shù)之和可以表示大于等于6 的全體偶數(shù)”，等價于“一切大于等于6 的偶數(shù)，均可表示為兩個質(zhì)數(shù)的和”，證畢。