化歸思想方法在偏微分方程求解中的應用

（南昌大學 數學系，江西 南昌 330031）

化歸思想方法是指將復雜難解或生疏未知的問題，通過某種轉化過程，歸結為簡單容易或熟悉已知的問題，從而使得原問題得以解決的一種思想方法.偏微分方程理論是預測自然現象變化和解決復雜工程技術問題的有力工具，主要研究偏微分方程定解問題的適定性、解的性質及求解方法等基本理論，成為現代數學中的一門重要分支.偏微分方程常見的求解方法包括特征線方法、行波變換方法、分離變量方法、球平均方法、降維方法、積分變換方法、變量變換方法、冪級數解方法、格林函數方法和數值解方法等[1-5].

化歸思想是偏微分方程理論中的重要思想方法，特別是在求偏微分方程的孤立子中具有廣泛的應用[6-10].本文以經典的KdV 方程為例，利用化歸思想方法求解KdV 方程的孤立子.首先，通過行波變換，將KdV方程轉化為一個可積的常微分方程，結合微分方程定性理論，直接求取KdV 方程的孤立波解；其次，通過極限轉化，將KdV 方程的周期波解轉化為孤立波解；最后，利用數學軟件Mathematica 模擬極限轉化過程.進一步地，通過此方法可以獲得KdV 方程的周期爆破波解和無界波解.

1 KdV 方程的孤立子

利用化歸思想方法求取KdV 方程的孤立子，包括行波變換和極限轉化等方法，并且通過數值模擬驗證極限轉化過程.

1.1 行波變換

考慮經典KdV 方程

通過行波變換

其中：c為正常數波速，可將方程（1）轉化為常微分方程

對式（3）兩邊同時關于變量ξ積分，可得

其中：g為積分常數.為了方便起見，不妨令g=0. 作變換φ′=y，則方程（4）可轉化為平面系統

根據微分方程定性理論，平面系統（5）是一個具有哈密頓函數

的哈密頓系統.

為得到系統（5）的平面相圖，令f(φ)=-3φ2+cφ，則函數f(φ)具有2個零點，分別為φ0=0，.

通過微分方程定性理論可知，(φ0,0)，(φ1,0)分別為系統（5）的鞍點和中心.進一步地，借助數學軟件Mathematica 可得到系統（5）的平面相圖（見圖1）.

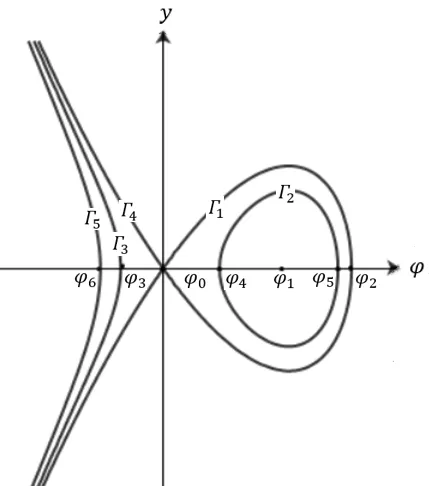
圖1 系統（5）的平面相圖

利用系統（5）的平面相圖，結合動力系統分支理論，可得方程（1）的孤立波解.

定理1對于任意給定的正常數c，方程（1）具有孤立波解

證明由圖1 可知，同宿軌Γ1過點(φ0,0)和(φ2,0)，其表達式為

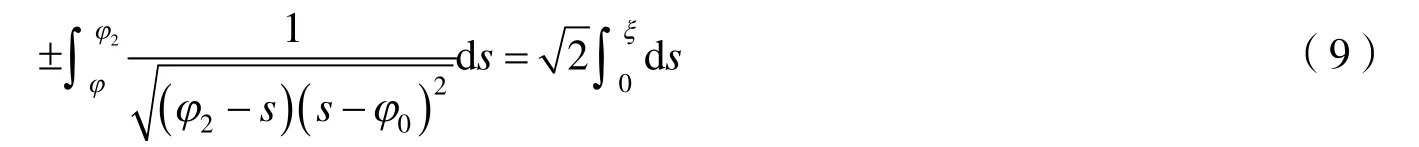
這里φ0＜φ＜φ2.通過對式（9）積分運算，結合行波變換式（2），可以得到方程（1）的孤立波解. 證畢.

1.2 極限轉化

由圖1 可以看出，當φ5向右趨于φ2時，軌道Γ2逼近軌道Γ1.因此可以通過極限轉化獲得方程（1）的孤立波解.

求閉軌道Γ2對應方程（1）的周期波解.注意到，過點(φ4,0)，(φ5,0)的閉軌道Γ2與過點(φ3,0)的特殊軌道Γ3具有相同的表達式，即

其中：φ1＜φ5＜φ2，且

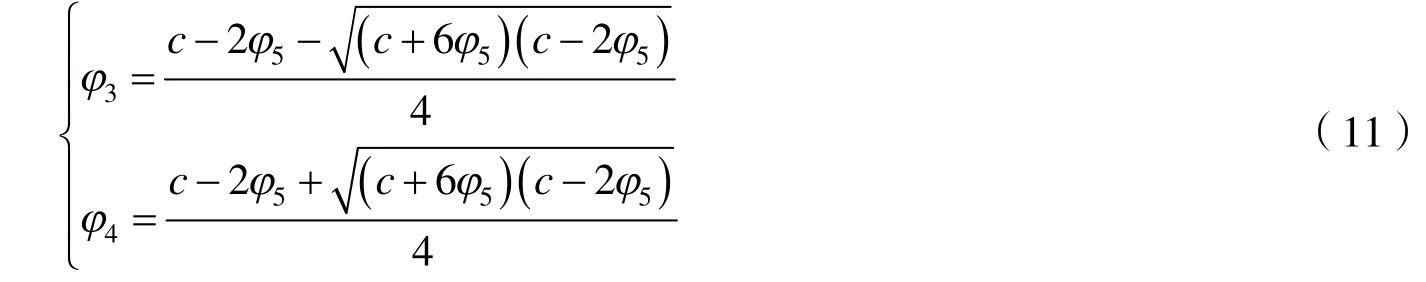
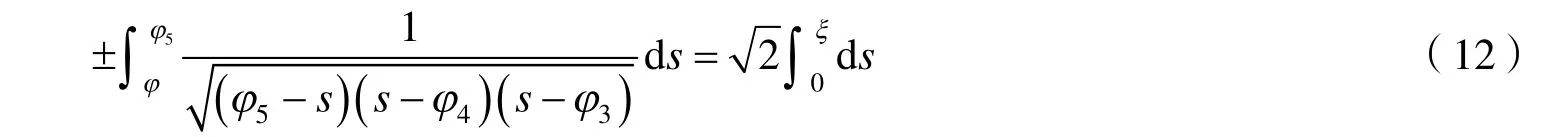
這里φ3＜φ4≤φ＜φ5，對式（12）進行積分變換運算，利用行波變換式（2），得到方程（1）的周期波解

其中

定理2當φ5→0.5c時，方程（1）的周期波解u2(x,t)趨于孤立波解u1(x,t)，即

證明由式（11）（13）（14）式可知，當φ5→0.5c時，有φ3→ 0，φ4→ 0，進而

1.3 數值模擬

通過數學軟件Mathematica 模擬定理2 中的極限轉化過程（見圖2），從而驗證了定理2 中的理論結果的正確性.

圖2 當c=2時，周期波解 u 2(x ,t)趨于孤立波解 u1 (x, t)的極限轉化過程

2 方法應用

利用化歸思想方法，同理可以解得特殊軌道Γ3，Γ4，Γ5分別對應KdV 方程的周期爆破波解u3(x,t)、無界波解u4(x,t)和周期爆破波解u5(x,t)，其表達式分別為

進一步地，通過極限轉化方法，可以得到周期爆破波解u3(x,t)趨于無界波解u4(x,t).證明過程類似于定理2，在此不再贅述.

3 結語

本文通過行波變換方法和極限轉化方法等化歸思想方法求解了經典KdV 方程的孤立子，并且通過數值模擬驗證了極限轉化方法的可行性.進一步地，應用此方法獲得了經典KdV 方程的其它精確行波解.化歸思想方法不僅可以求解經典KdV 方程的孤立子，而且適用于其它波動方程的求解問題，如mKdV 方程的孤立子和Camassa-Holm 方程的尖孤子，以及導出波動方程初值問題的達朗貝爾公式等求解問題，這為偏微分方程課程的教學提供了一些參考.