多關節機器人的反步法控制及仿真研究

李鵬 高述勇 楊杰 遲潔茹

摘要：??針對關節型機器人的軌跡跟蹤控制問題，本文設計了基于反步法的控制器。利用反步法將復雜的非線性機器人系統分解成兩個子系統，借助Lyapunov函數設計中間虛擬控制量，一直后推到整個系統，獲取控制系統實際的控制律，同時利用積分環節將每個子系統串聯起來，從而形成對整個系統的控制，并利用Lyapunov穩定性定理，證明了系統的穩定性。同時，以兩自由度關節型機器人為研究對象，搭建仿真控制系統進行仿真分析。仿真結果表明，反步法控制不僅具有良好的動態和穩態性能，而且魯棒性較強，說明該控制方法的軌跡跟蹤控制有效可行。該研究具有良好的應用前景。

關鍵詞：??關節型機器人;?反步法控制;?跟蹤控制;?穩定性

中圖分類號：?TP242.2?文獻標識碼：?A

收稿日期：?2018-11-27;?修回日期：?2019-09-20

作者簡介：??李鵬（1991-），男，山東臨沂人，碩士研究生，主要研究方向為測控技術及智能儀器。

通信作者：??楊杰（1967-），男，山東青島人，副教授，碩士生導師，主要研究方向為測控技術及智能儀器。Email：?jackiey69@sina.com

關節型機器人（即機械手臂），是工業領域中應用最廣泛的機器人類型之一，在裝配、搬運、焊接等工業領域發揮著重要的作用[1]。但由于機器人系統是一種復雜的非線性系統，耦合性強，傳動的轉矩控制以及PID等控制方法已經難以滿足工業化快速發展對機器人控制精度和速度的要求[2]。由于現代智能控制的快速發展，其在控制速度和精度上已遠遠高于傳統控制，但是在現代智能控制中仍然存在一些問題[3-4]。模糊控制無需建立精確的數學模型，魯棒性較強，但是在實際控制中卻存在穩態精度不夠的問題[5-8]。反饋線性化控制能夠將復雜的非線性系統解耦，線性化準確度高，但是易受外界干擾，魯棒性較差[9-10];無源控制具有全局穩定性且不存在奇異點等優點，但是一般只能借助阻尼的注入來設計控制器，使用其他方法，控制系統的穩定性將難以得到保證，且期望的哈密頓函數、互聯矩陣以及阻尼矩陣比較復雜[11-14];反步法，即后推法，通過設計虛擬控制律保證系統內核在穩定性等方面的性能，并通過不斷的修正虛擬控制律，實現系統的快速穩定的跟蹤，控制系統的搭建和系統的穩定性分析比較簡單，控制系統的動、靜性能優良。潘月斗等人[15]將反步法應用到矩陣變換器輸入側電流的控制，實現在負載變化存在的情況下對輸入側電流的快速跟蹤，有效的提高了控制系統的魯棒性;劉燕斌等人[16]將反步法應用到高超音速飛機縱向逆飛行控制中，實現了在具有嚴重非線性、強耦合的飛機縱向飛行控制以及對外界干擾的抑制，且能夠保證系統的全局穩定性;賀躍幫等人[17]將反步法應用到無人直升機的跟蹤控制中，實現了外界干擾以及建模誤差等存在情況下的軌跡跟蹤控制，使控制系統具有較強的魯棒性。基于此，本文設計了基于反步法的控制器，借助Lyapunov函數得到控制系統實際的控制律，同時利用Lyapunov穩定性定理，分析了控制系統的穩定性，并以二自由關節型機器人為研究對象，搭建了機器人仿真控制系統，驗證了反步法控制的有效性。

1?關節型機器人系統

對具有n個關節的剛性關節型機器人，其動態方程可用如下二階非線性微分方程描述[18]為

τ=M（q）+C（q，）（1）

式中，τ∈Rn為控制力矩;∈Rn為關節角位置矢量;∈Rn為關節角速度矢量;q∈Rn為關節角加速度矢量;M（q）∈Rn×n為機器人慣性矩陣;C（q，）∈Rn為機器人哥氏力與向心力矩陣。

2?關節型機器人反步法控制器設計

關節機器人的控制問題是指利用各關節的控制量，使各個關節能夠在較短的時間內跟蹤輸入信號，同時保證控制輸出的穩定性。定義如下非線性控制系統

1=f1（x1）+x22=f2（x1，x2）+x3i=fi（x1，…，xi）+xi+1n=fn（x1，…，xn-1，xn）+u（2）

式中，x為系統的狀態向量;u=u（x）控制系統的反饋控制輸入。

反步法的基本思想是通過將每個子系統i中的xi+1作為虛擬控制量，并通過適當的虛擬反饋xi+1=αi（i=1，2，…，n），使前面的狀態達到漸進穩定。但由于一般難以滿足xi+1=αi，因此需要引入誤差，從而通過控制作用保證xi+1與αi之間漸進穩定[19-20]。

利用系統的狀態與虛擬反饋，定義n個誤差為

e1=x1e2=x2-α1（x1）en=xn-αn-1（x1，x2，…，xn-1）（3）

式中，αi（i=1，2，…，n）為待定。通過Lyapunov函數構造，可以使每一個狀態分量能夠漸進的穩定。

為了便于使用反步法，定義機器人控制系統的狀態向量x1=q，x2=，系統的輸出y=x1，則非線性系統（1）可以表示為

1=x22=M-1（x1）τ-M-1（x1）Cx2y=x1（4）

采用反步法，設計關節型機器人控制器，其步驟如下：

步驟1?定義關節型機器人控制系統的輸出誤差為

e1=y-yd（5）

其中，yd為控制系統期望的輸出。對式（5）求導，可得

1=1-d=x2-d（6）

定義第1個子系統的虛擬控制量為

α1=-c1e1+d（7）

其中，c1為可調整的參數，且c1>0。

定義關節型機器人的虛擬控制誤差為

e2=x2-α1（8）

對第1個子系統定義Lyapunov函數為

V1=12e21（9）

則對式（9）求導，并結合式（6）可得

1=e11=e1（x2-d）=e1（e2+α1-d）（10）

將式（8）代入式（10）可得

1=-c1e21+e1e2（11）

如果e2=0，則1≤0，為此，進行下一步設計。

步驟2?對式（8）求導，并結合式（4）可得

2=M-1（x1）τ-M-1（x1）Cx2-1（12）

對第2個子系統定義Lyapunov函數為

V2=V1+12e22（13）

對式（13）求導可得

2=1+e22=-c1e21+e1e2+e22=-c1e21+e1e2+e2（M-1（x1）τ-M-1（x1）Cx2+c11-d1）（14）

為使2≤0，設計關節型機器人控制器的實際控制律為

τ=Cx2+M（x1）d-M（x1）c11-M（x1）e1-c2e2（15）

其中，c2為可調整的參數，且c2>0。則

2=-c1e21-c1e22≤0（16）

關節型機器人控制律的設計滿足Lyapunov穩定性定理的條件，使e1和e2漸進穩定，從而可以保證系統具有全局的漸進穩定。

3?仿真實驗

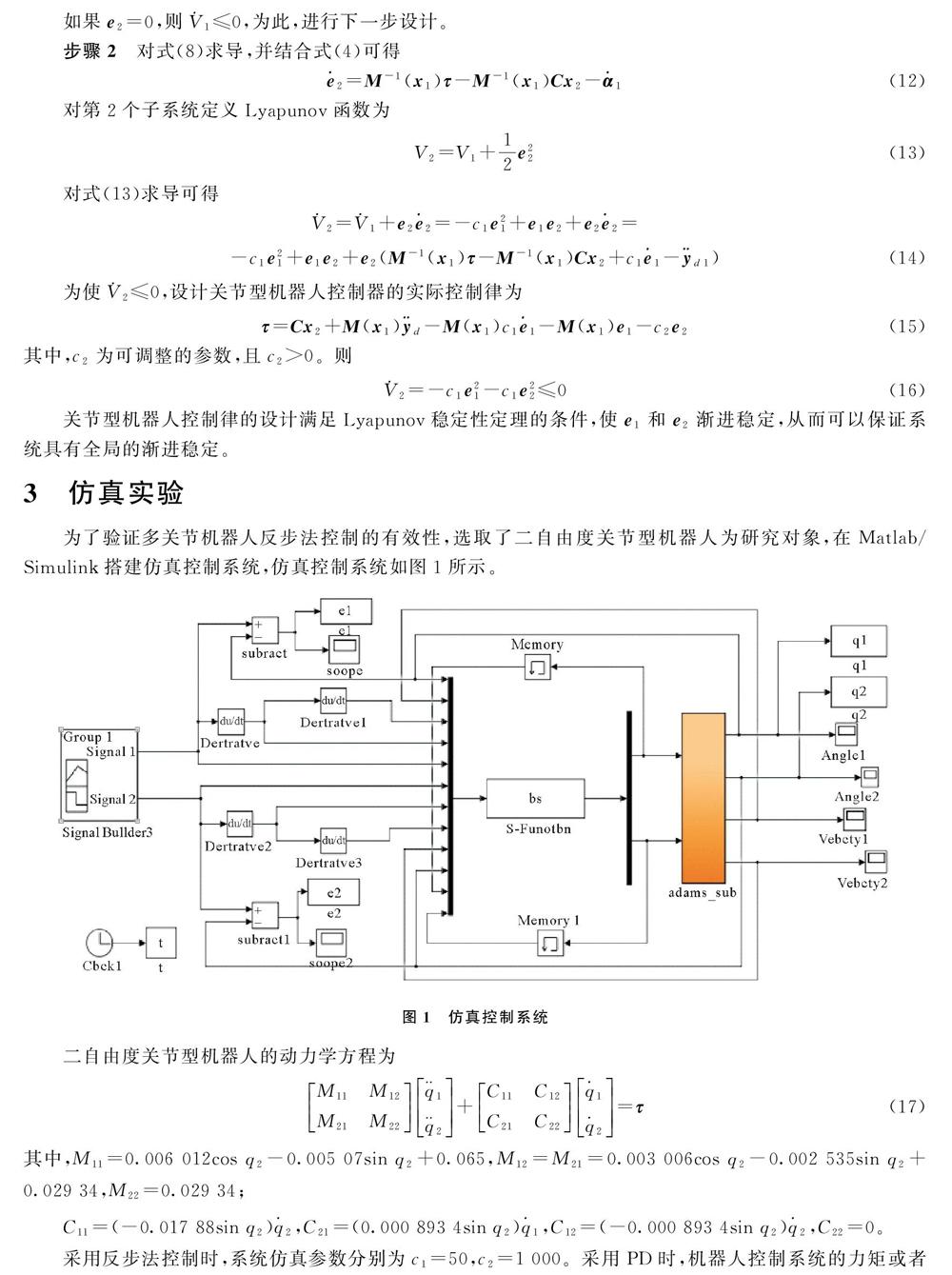
為了驗證多關節機器人反步法控制的有效性，選取了二自由度關節型機器人為研究對象，在Matlab/Simulink搭建仿真控制系統，仿真控制系統如圖1所示。

二自由度關節型機器人的動力學方程為

M11M12M21M2212+C11C12C21C2212=τ（17）

其中，M11=0.006?012cos?q2-0.005?07sin?q2+0.065，M12=M21=0.003?006cos?q2-0.002?535sin?q2+0.029?34，M22=0.029?34;

C11=（-0.017?88sin?q2）2，C21=（0.000?893?4sin?q2）1，C12=（-0.000?893?4sin?q2）2，C22=0。

采用反步法控制時，系統仿真參數分別為c1=50，c2=1?000。采用PD時，機器人控制系統的力矩或者力控制輸出為

τ=kpe+kd（18）

其中，τ為控制力矩或力;e為軌跡跟蹤誤差;kp為比例系數;kd為微分系數。

給定關節型機器人旋轉關節1和關節2的期望角度為qr1=qr2=1。采用反步法控制時，反步法控制關節1期望軌跡與實際軌跡如圖2所示，反步法控制關節2期望軌跡與實際軌跡如圖3所示。由圖2和圖3可以看出，反步法控制的跟蹤速度較快，能夠較快的到達穩態，而且到達穩態后，反步法控制的穩態精度較高，說明反步法控制具有良好的動態和穩態性能。

采用PD控制時，PD控制關節1期望軌跡與實際軌跡如圖4所示，PD控制關節2期望軌跡與實際軌跡如圖5所示。由圖4和圖5可以看出，PD控制的跟蹤速度比反步法控制跟蹤速度慢，且達到穩態時，PD控制比反步法控制的穩態精度低。

當t=0.6?s時，施加一個持續時間為0.01?s的干擾后，采用反步法控制時，干擾對反步法控制關節1軌跡曲線的影響如圖6所示，干擾對反步法控制關節2軌跡曲線的影響如圖7所示。

由圖6和圖7可以看出，在給各關節施加干擾后，采用反步法控制的波形波動較小，再次達到穩態所用的時間較短，說明反步法控制具有較強的魯棒性。

采用PD控制時，干擾對PD控制關節1軌跡曲線的影響如圖8所示，干擾對PD控制關節2軌跡曲線的影響如圖9所示。由圖8和圖9可以看出，采用PD控制的波形波動比反步法控制大，再次達到穩態所用的時間比反步法控制長。

由以上仿真結果可知，反步法控制具有更好的動態和穩態性能，且控制系統能夠更明顯的減弱外界干擾對機器人控制系統輸出的影響，魯棒性更強，說明該控制方法有效，符合設計的要求。

4?結束語

本文針對多關節機器人的軌跡跟蹤控制，提出了反步法控制。選取二自由度關節型機器人為研究對象，在Matlab/Simulink中搭建控制系統，進行仿真實驗，并將反步法控制與傳統的PD控制進行比較。仿真結果表明，當系統存在外界干擾時，與傳統的PD控制相比，反步法控制系統的輸出波形變化較小，說明反步法控制能夠更強的抑制外界干擾影響，具有更強的魯棒性;同時與傳統PD控制相比，反步法控制的輸出能夠更快的跟蹤輸入信號，且穩態精度更高，說明反步法控制具有更好的動態和穩態性能，因此該控制方法是可行有效的。

參考文獻：

[1]?陳培華，?曹其新.?基于逆動力學方法的關節型機器人軌跡控制[J].?華中科技大學學報：?自然科學版，?2013，?41（z1）：?17-20，?24.

[2]?夏長亮，?張天一，?周湛清，?等.?結合開關表的三電平逆變器永磁同步電機模型預測轉矩控制[J].?電工技術學報，?2016，?31（20）：?83-92，?110.

[3]?Chen?F?Y，?Jiang?R?Q，?Zhang?K?K，?et?al.?Robust?backstepping?slidingmode?control?and?observerbased?fault?estimation?for?a?quadrotor?UAV[J].?IEEE?Transactions?on?Industrial?Electronics，?2016，?63（8）：?5044-5056.

[4]?Li?S?S，?Wang?Y?N，?Tan?J?H，?et?al.?Adaptive?RBFNNs/integral?sliding?mode?control?for?a?quadrotor?aircraft[J].?Neurocomputing，?2016，?216：?126-134.

[5]?胡包鋼，?應浩.?模糊PID控制技術研究發展回顧及其面臨的若干重要問題[J].?自動化學報，?2001，?27（4）：?567-584.

[6]?余躍慶，?梁浩，?張卓.?平面4自由度欠驅動機器人的位置和姿態控制[J].?機械工程學報，?2015，?51（13）：?203-211.

[7]?郭偉斌，?陳勇.?基于模糊控制的除草機器人自主導航[J].?機器人，?2010，?32（2）：?204-209.

[8]?李鵬，?楊杰，?牛歡.?二自由度機器人模糊滑模位置控制及仿真[J].?青島大學學報：?工程技術版，?2017，?32（2）：?102-107.

[9]?呂學勤，?張軻，?吳毅雄，?等.?輪式移動焊接機器人輸出反饋線性化控制[J].?機械工程學報，?2014，?50（6）：?48-54.

[10]?賴旭芝，?蔡暢，?吳敏，?等.?基于部分反饋線性化的三桿體操機器人控制策略[J].?高技術通訊，?2009，?19（12）：?1270-1275.

[11]?錢甜甜，?苗世洪，?劉子文，?等.?基于PCHD模型的VSCHVDC的無源控制及滑模輔助改進控制[J].?電工技術學報，?2016，?31（3）：?138-144.

[12]?魯偉，?徐長波，?李春文，?等.?并聯混合有源濾波器哈密頓系統建模及無源控制[J].?控制理論與應用，?2012，?29（11）：?1397-1402.

[13]?程啟明，?郭凱，?程尹曼，?等.?電壓不平衡下雙饋感應發電機機側變換器無源控制方法[J].?電力系統自動化，?2016，?40（19）：?73-81.

[14]?劉英培，?梁海平，?栗然，?等.?基于無源性與自抗擾控制的雙饋風力發電系統研究[J].?電工技術學報，?2015，?30（18）：?121-130.

[15]?潘月斗，?郭凱，?陳繼義，?等.?矩陣變換器輸入側電流的反步法控制[J].?華南理工大學學報：?自然科學版，?2015，?43（12）：?18-24，?47.

[16]?劉燕斌，?陸宇平.?基于反步法的高超音速飛機縱向逆飛行控制[J].?控制與決策，?2007，?22（3）：?313-317.

[17]?賀躍幫，?裴海龍，?周洪波，?等.?干擾下的無人直升機自適應反步法魯棒跟蹤控制[J].?控制理論與應用，?2013，?30（7）：?834-843.

[18]?賈凱凱，?梅江平，?劉松濤，?等.?4自由度并聯機構剛體動力學模型[J].?機械工程學報，?2016，?52（13）：?10-16.

[19]?Nikdel?N，?Badamchizadeh?M?A，?Azimirad?V，?et?al.?Adaptive?backstepping?control?for?an?ndegree?of?freedom?robotic?manipulator?based?on?combined?state?augmentation[J].?Robotics?&?Computer?Integrated?Manufacturing，?2017，?44：?129-143.

[20]?Yacef?F，?Bouhali?O，?Hamerlain?M，?et?al.?Observerbased?adaptive?fuzzy?backstepping?tracking?control?of?quadrotor?unmanned?aerial?vehicle?powered?by?liion?battery[J].?Journal?of?Intelligent?&?Robotic?Systems，?2016，?84（1/4）：?1-19.

Control?and?Simulation?of?MultiLink?Robots?Based?on?Backstepping

LI?Penga，?GAO?Shuyonga，?YANG?Jiea，?CHI?Jierub

（a.?School?of?Electromechanic?Engineering;?b.?School?of?Electronic?Information，?Qingdao?University，?Qingdao?266071，?China）

Abstract：??Aiming?at?the?tracking?control?of?multilink?robots，?a?controller?based?on?backstepping?is?designed.?Backstepping?method?can?decompose?the?nonlinear?robot?system?into?two?subsystems.?And?by?the?use?of?Lyapunov?function，?we?can?design?inter?virtual?control?variables，?until?back?to?the?whole?system.?Then?by?the?use?of?the?Lyapunov?function，?we?can?obtain?the?actual?control?law?of?the?control?system.?Each?subsystem?is?connected?in?series?by?the?use?of?integral?part，?thus?it?can?realize?the?control?of?entire?system.?The?Lyapunov?stability?theorem?is?used?to?prove?the?stability?of?the?system.?The?simulation?results?show?that?the?backstepping?method?not?only?has?good?dynamic?and?steadystate?performance，?but?also?has?strong?ability?to?suppress?the?external?interference.?The?simulation?results?indicate?that?the?trajectory?tracking?control?of?backstepping?is?effective?and?feasible.?The?control?method?has?a?good?application?prospect.

Key?words：??multilink?Robots;?backstepping?control;?tracking?control;?stability