基于詞頻統計算法的中英文詞頻分布研究

李杰 孫仁誠

摘要：??針對冪律判斷方式存在的問題，本文基于早期對冪律分布的研究，結合最大擬然擬合方法及詞頻統計算法，對中英文詞頻分布進行研究。給出了雙對數坐標系下冪律分布的判斷，并對詞頻統計與冪律分布進行擬合。研究結果表明，在雙對數坐標系下，分布圖像為近似直線是判斷冪律分布的必要條件，而非充分條件;在自然語言的詞頻統計分布模型上，對觀測數據進行冪律分布的擬合，得出的pvalue分別為0.14和0.19，均大于0.1，且泊松分布、指數分布、廣延指數分布的pvalue值都為0，即可排除滿足其他分布的假設，因此對觀測數據擬合效果最好的是冪律分布。說明自然語言的詞頻分布滿足冪律，且中英文同樣適用。該研究對人們認識語言的發展過程具有重要意義。

關鍵詞：??詞頻統計;?冪律分布;?最大似然估計;?KS統計量

中圖分類號：?TP312;?C81?文獻標識碼：?A

收稿日期：?2019-06-20;?修回日期：?2019-10-28

基金項目：??國家自然科學青年基金資助項目（41706198）

作者簡介：??李杰（1994-），男，碩士研究生，主要研究方向為數據挖掘與分析。

通信作者：??孫仁誠（1977-），男，副教授，博士，主要研究方向為數據挖掘及人工智能。Email：?qdsunstar@163.com

冪律分布[1]廣泛存在于計算機科學、人口統計學與社會科學、物理學、經濟學與金融學等眾多領域中，且形式多樣。實驗證明，在自然界與日常生活中，包括地震規模大小的分布、月球表面上月坑直徑的分布、行星間碎片大小的分布、太陽耀斑強度的分布、計算機文件大小的分布、戰爭規模的分布、人類語言中單詞頻率的分布、大多數國家姓氏的分布、科學家撰寫的論文數的分布、論文被引用的次數的分布、網頁被點擊次數的分布[2]、書籍及唱片的銷售冊數或張數的分布、電力數據的分布[3]、甚至電影所獲得的奧斯卡獎項數的分布等都是典型的冪律分布。但這一結果存在巨大缺陷，曾經被認為滿足冪律分布的某些數據，只有在一定的條件范圍內才是冪律，而在整體大量的數據集上是不純的[4]。20世紀中期，對于冪律分布的研究，一些研究者[5-6]分別在語言學和經濟學的領域提出了著名的80/20定律。這一定律的基本形式即為簡單的冪函數，是冪律分布的4種形式之一，其他形式的冪律分布有名次-規模分布、規模-概率分布等。直到21世紀初，A.L.Barabasi等人[7-8]提出了無標度理論，從復雜網絡的角度探究了冪律分布的性質，即無標度網絡的度分布就是冪律分布，為復雜網絡的發展奠定了理論基礎;C.?Aaron等人[4]對冪律分布的判斷標準進行了詳盡的理論證明，推翻了前人通過雙對數坐標系下是否構成一條近似直線判斷冪律分布的方法，并證明了雙對數坐標系下近似直線是冪律分布的必要條件。關于中英文詞頻分布的研究[9-11]一直是自然語言處理的重點。國內中文分詞的算法主要集中在詞典與統計相結合[12]的方式，但精度有待提升。2017年，麻省理工學院的Sun?Junyi團隊歷時4年，完善了新的詞頻統計算法，與傳統的基于統計的詞頻算法＼[13＼]不同，新的算法是基于前綴詞典來實現詞圖掃描，構造有向無環圖（directed?acyclic?graph，DAG），利用動態規劃算法查找詞頻最大切合組，同時結合隱馬爾可夫模型（hidden?markov?model，HMM）模型操作未登錄詞，大大提高了分詞精度和分詞效率。基于此，本文在最新詞頻統計算法基礎上，構造私有的前綴詞典及DAG，同時采用最新的冪律分布研究方式，對中英文兩種語言進行研究，完善了之前研究者們[14-16]在詞頻統計精度及冪律分布判斷方式上的不足之處，并進行了可視化的冪律擬合。該研究推動了人們對自然語言發展的認識。

1?冪律分布的研究

1.1?雙對數坐標系下冪律分布的判斷

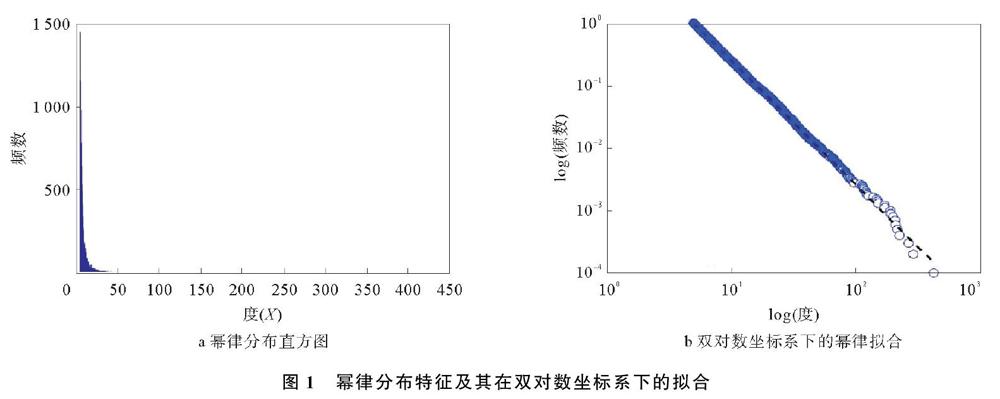
20世紀末，人們對冪律分布的研究是基于雙對數坐標系下，數據分布的圖像是否為一條近似的直線來判斷。冪律分布特征及其在雙對數坐標系下的擬合如圖1所示。

其形式化的表達為：y=cx-r，其中x，y表示正的隨機變量;c，r為常數且均大于零。這種分布特征只有少數事件的規模比較大，而絕大多數事件的規模較小。對y-cx-r兩邊取對數，可知lny與lnx滿足lny=lnc-rlnx，這是一種線性關系，即在雙對數坐標系下，冪律分布可以通過一條斜率為負的冪指數的直線進行擬合，這一線性關系是判斷給定的實例中隨機變量是否滿足冪律的依據。

判斷兩個隨機變量是否滿足線性關系，可以求解兩者之間的相關系數;利用一元線性回歸模型和最小二乘法，可得lny對lnx的線性回歸方程，從而得到y與x之間的冪律關系式[1，4]。

對于在雙對數坐標系下，線性關系判斷數據是否滿足冪律分布的說法不正確，因為雙對數坐標系下的線性關系是數據滿足冪律分布的必要條件，而不是充分條件。

1.2?冪律分布的判斷

2007年，Aaron?chauset等人[4]提出了判斷冪律分布的一系列方法，其思想是將最大似然擬合方法與基于KolmogorovSmirnov（KS）統計以及似然比的擬合優度檢驗相結合，判斷觀測數據是否滿足冪律分布，過程主要分為以下幾部分：

1）?估計冪律模型的參數xmin和α。

2）?計算數據與冪律之間的擬合優度，如果得到的p-value值大于0.1，則冪律分布是觀測數據的似然假設，否則拒絕該假設。

3）?通過似然比檢驗，將冪律與其他假設進行比較。對于每個備選方案，如果計算的似然比與零顯著不同，則其符號表示該備選方案是否優于冪律模型。

2?詞頻統計與冪律分布擬合

關于自然語言中詞匯的分布特征，早在20世紀中葉就有研究者進行過大量研究，直至20世紀末，有學者（冪律分布研究簡史）通過雙對數坐標系下圖像近似一條直線的擬合方式，說明數據滿足冪律分布，這種方式顯然缺乏說服力。本文基于文獻＼[4＼]提出的方法，首先基于詞頻統計算法對文本進行統計，然后結合最大似然擬合方法[17]與基于KolmogorovSmirnov（KS）統計[18]以及似然比[19]的擬合優度檢驗方式，對自然語言進行冪律分布的擬合。

關于數據的選擇，本文選取了經典文學作品《飄》的中英文對照版本，分別對英文和中文進行詞頻統計，并擬合冪律分布。

2.1?詞頻統計算法

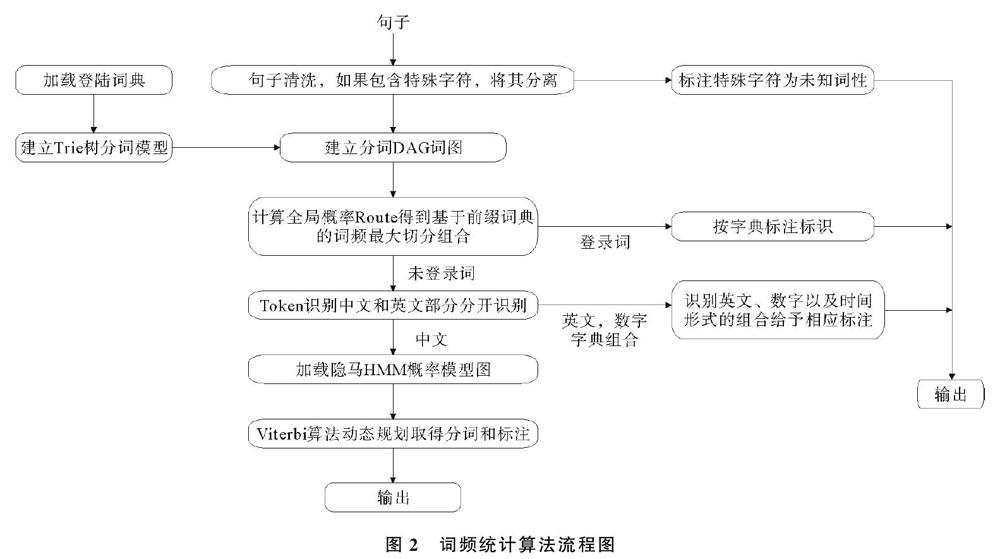
詞頻統計算法流程圖如圖2所示，詞頻統計算法整體分為3個部分，每個部分又可分為多個步驟，其描述如下：

1）?基于Trie樹結構實現高效的詞圖掃描，構造出有向無環圖（DAG），圖中包括生成句子中漢字所有可能的成詞情況。根據dict.txt生成trie樹，字典在生成trie樹的同時，也把每個詞的出現次數轉換為頻率;對需要進行分詞的句子，根據已經生成的trie樹，生成有向無環圖（DAG），簡言之，就是將句子根據給定的詞典進行查尋操作，生成多種可能的句子切分。

2）?用動態規劃算法查找最大概率路徑，找到基于詞頻的最大切分組合。查找待分詞句子中已經切分好的詞語，即查找該詞語出現的頻率，如果查不到該詞，就把該詞的頻率賦值為詞典中出現頻率最小的那個詞語的頻率;根據動態規劃算法查找最大概率路徑，即對句子從后往前反向計算最大概率，P（NodeN）=1.0，P（NodeN-1）=P（NodeN）*Max（P（最后一個詞））…依次類推，得到最大概率路徑，從而得到最大概率的切分組合。

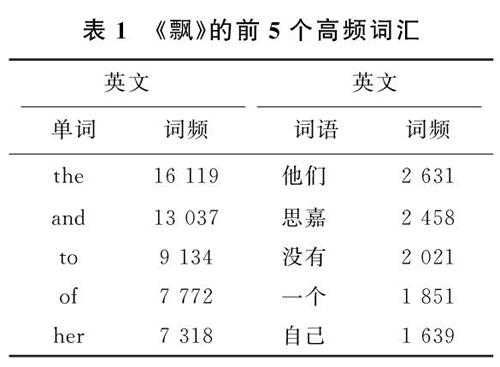
3）?對于詞典中未錄入的詞，采用基于漢字成詞能力的HMM模型，同時使用viterbi算法。中文詞匯按照BEMS四個狀態標記，B代表begin，即開始位置，E代表end，即結束位置，M代表middle，表示中間位置，S代表singgle，是單獨成詞的位置，如山東可表示為BE，即山/B，是開始位置，東/E，是結束位置;對語料庫進行初步訓練，得到3個概率表，并結合viterbi算法，可以得到一個概率最大的BEMS序列，按照B開始，E結尾的方式，對分詞的句子重新組合，就能得到最終的分詞結果[14]。對《飄》的中英文對照版詞頻進行統計，《飄》的前5個高頻詞匯如表1所示。

由表1可以看出，中英文在表達同義內容時，所使用詞匯差別巨大，并未出現高頻詞匯一致性的現象，這與語言的特點有關。同時，英文的代詞和介詞在使用率上遠高于其他詞匯，而中文則不同，除代詞外，量詞在文章中也高頻出現。雖然有諸多的差別，但在分布情況上仍需進一步驗證。

2.2?冪律分布擬合

本文通過將最大似然擬合方法與基于KolmogorovSmirnov（KS）統計以及似然比的擬合優度檢驗相結合的方式，對自然語言進行了冪律分布擬合。中英文詞頻在雙對數坐標系下的冪律擬合如圖3所示。圖3中，英文詞頻xmin=40，α=1.89;中文詞頻xmin=38，α=2.1。

由圖3可以看出，在雙對數坐標系下，中英文的詞頻分布均呈現一條近似的直線，說明存在冪律分布的可能性，但需要驗證pvalue是否大于0.1，如果大于0.1，就要進一步排除其他分布是否比冪律分布擬合效果更好，否則，可以直接判斷不滿足冪律分布。似然比的擬合優度LR值和pvalue（p）值如表2所示。

由表2可以看出，對觀測數據進行冪律分布的擬合，得出的pvalue分別為0.14和0.19，均大于0.1，且泊松分布，指數分布，廣延指數分布的pvalue值都為0，即滿足其他分布的假設可直接排除，因此對觀測數據擬合效果最好的是冪律分布。

3?結束語

本文通過對中英文詞頻的統計分析，證明了自然語言中的詞匯在日常生活中的使用頻率是服從冪律分布的，即部分詞匯會被大量使用，大部分詞匯的使用頻率較低，符合動力學中的省力原則，人們更傾向于用更少詞匯的不同組合來表達不同的意思，對認識語言的發展過程具有重要意義。這一結論不僅僅出現在本文所研究的文獻中，對于其他文獻同樣適用。文中詞頻統計算法和“最大似然擬合方法”、“KS統計以及似然比的擬合優度檢驗方法”的結合，使本結論的精確度更高，進一步補充了前人對于詞頻分布的研究與應用。在接下來的工作中，可以將重點放在對其他語言的研究上，在冪律分布的基礎之上，探究是否有更加精確的擬合方式，進一步推動人們對于自然語言發展的認識。

參考文獻：

[1]?胡海波，?王林.?冪律分布研究簡史[J].?物理，?2005，?34（12）：?889-896.

[2]?Adamic?L?A，?Huberman?B?A，?Barabási?A?L，?et?al.?Powerlaw?distribution?of?the?world?wide?web[J].?Science，?2000，?287?（5461）：?2115a.

[3]?王冠男，?鄧春宇，?趙悅，?等.?電力數據中的冪律分布特性[J].?電信科學，?2013，?29（11）：?109-114，?121.

[4]?Aaron?C，?Cosma?R?S，?Newman?M?E?J.?Powerlaw?distributions?in?empirical?data[J].?Siam?Review，?2009，?0706（1062）：?661-703.

[5]?嚴怡民.?情報學概論[M].?武漢：?武漢大學出版社，?1994.

[6]?Arnold?B?C.?Pareto?Distribution[M]∥Encyclopedia?of?Statistical?Sciences.?United?States：?John?Wiley?&?Sons，?Inc.，?2006.

[7]?Barabasi?A?L，?Albert?R.?Emergence?of?scaling?in?random?networks[J].?Science，?1999，?286（5439）：?509-514.

[8]?Barabasi?A?L，?Bonabeau?E.?Scalefree?networks[J].?Scientific?American，?2003，?288（5）：?60.

[9]?張丹.?中文分詞算法綜述[J].?黑龍江科技信息，?2012（8）：?206.

[10]?張華平，?劉群.?基于N-最短路徑方法的中文詞語粗分模型[J].?中文信息學報，?2002，?16（5）：?1-7.

[11]?費洪曉，?康松林，?朱小娟，?等.?基于詞頻統計的中文分詞的研究[J].?計算機工程與應用，?2005，?41（7）：?67-68，?100.

[12]?秦贊.?中文分詞算法的研究與實現[D].?長春：?吉林大學，?2016.

[13]?祝永志，?荊靜.?基于Python語言的中文分詞技術的研究[J].?通信技術，?2019，?52（7）：?1612-1619.

[14]?Goldstein?M?L，?Morris?S?A，?Yen?G?G.?Fitting?to?the?powerlaw?distribution[J].?The?European?Physical?Journal?BCondensed?Matter?and?Complex?Systems，?2004，?41（2）：?2004.

[15]?Fernholz?R?T.?Nonparametric?methods?and?locatimebased?estimation?for?dynamic?power?law?distributions[J].?Journal?of?Applied?Econometrics，?2016，?32（7）：?1244-1260.

[16]?Montebruno?P，?Bennett?R?J，?van?Lieshout?C，?et?al.?A?tale?of?two?tails：?Do?power?law?and?lognormal?models?fit?firmsize?distributions?in?the?midvictorian?era[J].?Physica?A：?Statistical?Mechanics?and?its?Applications，?2019，?523：?858-875.

[17]?胡德，?郭剛正.?最小二乘法、矩法和最大似然法的應用比較[J].?統計與決策，?2015（9）：?20-24.

[18]?Lilliefors?H?W.?On?the?kolmogorovsmirnov?test?for?normality?with?mean?and?variance?unknown[J].?Journal?of?the?American?Statistical?Association，?1967，?62（318）：?399-402.

[19]?成平.?極大似然估計與似然比檢驗的幾點注記[J].?應用概率統計，?2003，?19（1）：?55-59.

Research?on?Chinese?and?English?Word?Frequency?Distribution?Based?on?Word?Frequency?Statistics?Algorithm

LI?Jie，?SUN?Rencheng

（College?of?Computer?Science?&?Technology，?Qingdao?University，?Qingdao?266071，?China）

Abstract：??Aiming?at?the?problems?existing?in?the?power?law?judgment?method，?this?paper?studies?the?frequency?distribution?of?Chinese?and?English?words?based?on?the?previous?research?on?power?law?distribution，?combined?with?the?maximum?likelihood?fitting?method?and?word?frequency?statistics?algorithm.?The?judgment?of?power?law?distribution?in?double?logarithmic?coordinate?system?is?given，?and?the?word?frequency?statistics?and?power?law?distribution?are?fitted.?The?results?show?that?in?the?double?logarithmic?coordinate?system，?the?distribution?image?being?an?approximate?straight?line?is?a?necessary?condition?for?judging?the?power?law?distribution，?but?not?a?sufficient?condition.?On?the?word?frequency?statistical?distribution?model?of?natural?language，?the?power?law?distribution?of?the?observation?data?is?proposed.?The?pvalues?obtained?are?0.14?and?0.19，?respectively，?both?greater?than?0.1，?and?the?pvalues?of?the?Poisson?distribution，?the?exponential?distribution，?and?the?extensive?exponential?distribution?are?all?0，?that?is，?the?assumptions?satisfying?other?distributions?can?be?directly?excluded.?The?best?fit?for?the?observation?data?is?the?power?law?distribution.?It?shows?that?the?word?frequency?distribution?of?natural?language?satisfies?the?power?law，?and?both?Chinese?and?English?are?applicable.?This?research?is?of?great?significance?for?people?to?understand?the?development?process?of?language.

Key?words：??word?frequency?statistics;?power?law?distribution;?maximum?likelihood?estimation;?KS?statistics