基于CFD的礦用通風機風動特性和結構優化

馬玉華12

(1.山東科技大學， 山東青島 266427； 2.青島黃海學院， 山東青島 266590)

引言

礦用通風機是煤礦生產中最重要的設備之一，是確保井下采煤工作面空氣質量和溫度的關鍵。一般地，每開采1 t煤炭至少需要通風機提供4～6 t的新鮮空氣。通風機設備的持續運轉將消耗大量的電能，約占總煤礦機電設備功耗的8%～15%。高效節能是煤礦生產的基本要求[1]，也是國家可持續發展的重要戰略手段。根據礦井通風機的工作原理可知，葉片結構是決定風動效率的關鍵[2]，也是影響風機設備能耗的最重要因素之一。因此，通過對通風機風動特性和葉片結構優化的研究實現工作能力的提升具有顯著的經濟效益和社會效益。目前，基于靜強度特性的通風機結構優化(降低葉片質量或增加特殊結構) 仍是主要的研究手段比如，張明輝[3]采用遺傳算法建立MATLAB與ANSYS的交互機制，將葉片重量顯著降低；冀春俊[4]提出在通風機葉輪輪盤側添加凸臺結構，采用ANSYS分析整體的受力情況，減小了葉輪的變形量；丁鐵華[5]對某風機葉輪進行應力強度和變形分析，并根據計算結果找出強度和剛度較薄弱部位分別進行結構改進。在先進的生產工藝條件下，僅進行強度分析明顯無法滿足風機的高效節能要求。為此，采用CFD方法，對通風機的風動特性進行研究和分析，通過葉片結構的優化設計，提升風動效率。

1 CFD模型的構建與分析

1.1 風動特性參數

軸流式礦井風機實現的空氣流入和流出方向均近似平行于軸向，空氣的流場特性由葉片決定，基于CFD的流體數值模擬可計算出整個流體模型的風動特性參數。對于風機葉片而言，關鍵的風動特性參數包括全壓值、全壓系數、全壓效率和流量系數。

全壓值p0是指礦井通風機出口端面空氣壓力pout和入口端面空氣壓力pin的差，計算表達式為：

p0=pout-pin

(1)

全壓系數η是指礦井通風機的全壓值和動壓值的比值，計算表達式為：

(2)

式中，ρ—— 氣流密度，kg/m3

ut—— 葉片最外緣的線速度，m/s

通風機的全壓效率ζ為：

(3)

式中，q—— 通風機的氣體流量，m3/h

Tt—— 通風機的扭矩，N·m

ω—— 葉片角速度，rad/s

通風機的流量系數ψ為：

(4)

式中，D為通風機葉片外徑，m。

1.2 流體模型建立

軸流式礦井通風機主要由柱狀外殼、驅動部、葉輪和導葉等部件組成，如圖1所示。通風機工作時，空氣在葉輪作用下的獲取動能，葉片克服空氣阻力做功，流速方向近似于軸向。最終，通過導葉的壓力將風機出口段的氣流轉化為靜壓能，同時保證風動方向的穩定性。

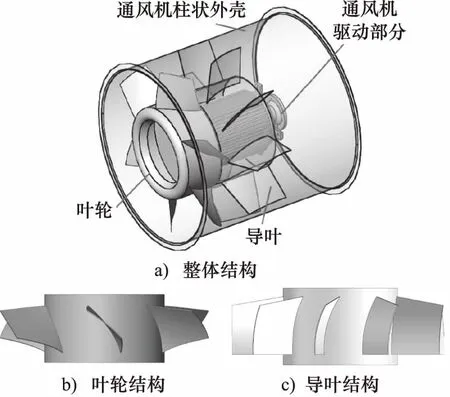
圖1 軸流式礦井通風機的結構模型

在CFD分析方法中，合理的湍流模型是確保計算精度的關鍵[6]。k-ε模型是最早出現的湍流模型之一，可滿足大部分工程精度要求。隨著CFD理論和技術的發展，在k-ε模型的基礎上衍生出RNG模型[7]和realizable模型[8]。根據風機CFD模型的特點，優先選用采用RNG模型，因為模型內的ε方程具有更完備的邊界條件，可處理葉片的湍流漩渦問題[9]，對于近壁計算更為可靠。對于通風機模型而言，屬于典型的高湍流復雜模型，因此采用壁面函數法更適合。在求解器設置方面，綜合考慮CFD模型的計算精度和效率，采用二階迎風格式和SIMPLE 算法實現控制方程的分離和求解。

1.3 網格校驗

網格質量是確保計算精度和迭代收斂性的關鍵。建立礦用軸流式通風機的CFD分析模型如圖2所示，為了便于網格劃分，將其分為入口計算域、葉輪計算域和出口計算域等三部分。其中，入口計算域和出口計算域均為空氣的充分流動或發展狀態。

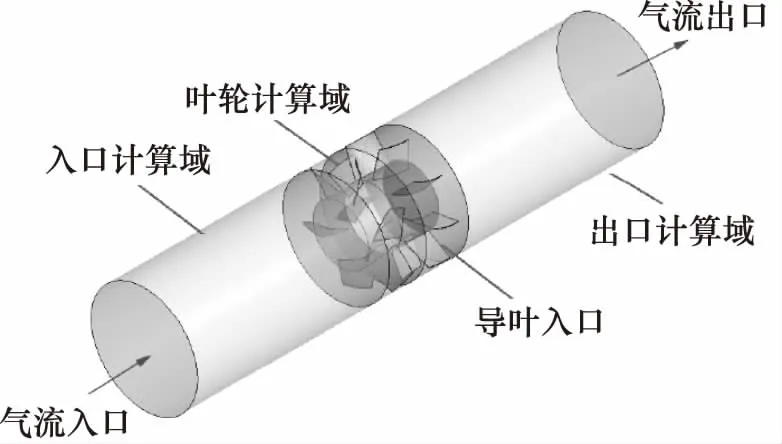
圖2 CFD分析模型

在所劃分的三部分區域中，葉輪計算域為流體動區域[10]，其他區域為靜區域，各個區域之間的連接采用interface進行定義。根據風機結構可知，葉片具有扭曲性，厚度只有4 mm，因此采用非結構化網格，不僅更能適應復雜曲面，而且可獲得良好的收斂性。考慮到計算效率，流體入口和出口區域采用結構化網格，葉輪計算域采用非結構化網格，其中，風機葉輪和導葉的局部網格如圖3所示。為了進一步確保整個CFD仿真的可靠性、收斂性和高效性，對網格密度進行關系檢驗。以全壓值為依據，逐漸增加網格數量，試算結果表明，當網格遞增至302萬左右時，全壓值幾乎不再發生變化，此時，網格密度對計算精度的影響可近似忽略。

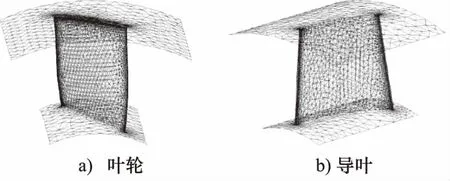
圖3 局部網格結構

1.4 模型參數特性

對于通風機結構而言，風機葉片在葉高斷面處的弦長l、風機入口處的氣流角γ1和出口處的氣流角γ2是決定風機形狀的關鍵參數。這3個參數中，風機入口處的氣流角γ1在數值上為出口處的氣流角γ2和滯后角α的和。其中，滯后角α是反映葉片幾何形狀的重要參數之一，與弦長l密切相關。為此，以滯后角α(12°，14°和16°)為主要的結構設計變量，通過CFX軟件計算全壓效率、全壓系數以及流量系數之間的內在聯系，并評價不同滯后角條件下的風動特性。

2 風動特性結果分析

2.1 風動參數

不同滯后角條件下，全壓系數η與全壓效率ζ之間的關系曲線如圖4所示。可以看出：三種滯后角中，14°滯后角的葉片全壓效率最高，當全壓系數等于0.33時為最大值；在全壓系數低于0.3時，12°滯后角和16°滯后角葉片的全壓效率差別非常小。

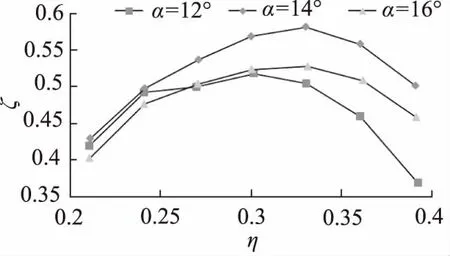
圖4 全壓系數與全壓效率關系曲線

不同滯后角條件下，全壓系數η與流量系數ψ之間的關系曲線如圖5所示。可以看出隨著流量系數的增大，全壓系數先增大后減小；當通風機的空氣流量較小時，不同滯后角條件下的全壓系數差別不大；當風量較大時，不同滯后角條件下的流量系數與全壓系數近似為線性關系，這與流量設計要求匹配。

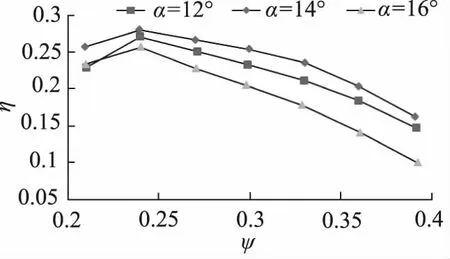
圖5 全壓系數與流量系數關系曲線

2.2 出口壓力

出口壓力是衡量葉片風動性能的重要參數，可作為評價風機工作穩定性的標準之一。不同滯后角條件下，徑向葉高百分比H與出口靜壓pTo之間的關系曲線如圖6所示。可以看出：隨著葉片尺寸在徑向方向的增大，靜壓表現出遞增變化趨勢；14°滯后角的靜壓值最小且變化緩慢，壓力梯度較小，表明空氣在該結構葉輪輪轂的流動加載情況更佳；在徑向葉高百分比20%～40%范圍內，存在靜壓平衡階段。

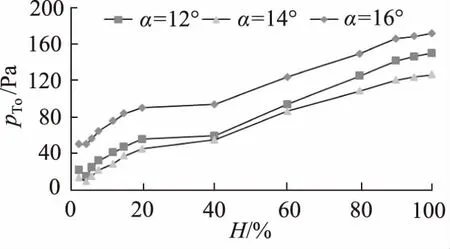
圖6 徑向葉高百分比與出口靜壓關系曲線

不同滯后角條件下，徑向葉高百分比H與出口動壓pDo之間的關系曲線如圖7所示。可以看出：12°滯后角的動壓值最小，但與14°滯后角的動壓值差別不大；徑向葉高百分比小于80%的范圍為動壓平衡階段，壓力值基本保持不變。

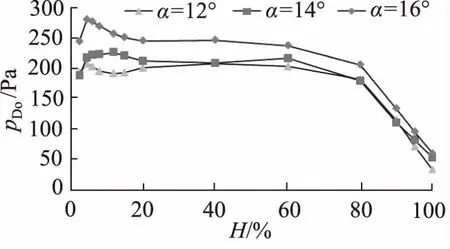
圖7 徑向葉高百分比與出口動壓關系曲線

2.3 出口速度

不同滯后角條件下，可得出徑向葉高百分比與出口速度關系曲線如圖8所示。可以看出：不同滯后角葉片的軸向出口速度vb均隨著徑向葉高百分比的增大表現出先增大后減小的趨勢，從數值上看，滯后角對于軸向出口速度的大小幾乎沒有影響；14°滯后角和16°滯后角的法向出口速度vb在數值上基本一致，均顯著大于12°滯后角葉片(vb出現負數是因為該位置的圓周速度較小，離心力不足以平衡逆壓梯度)；在葉頂和葉根位置，不同滯后角條件下的出口初速基本相同；從整體上分析，出口速度隨著滯后角的增大而增大。

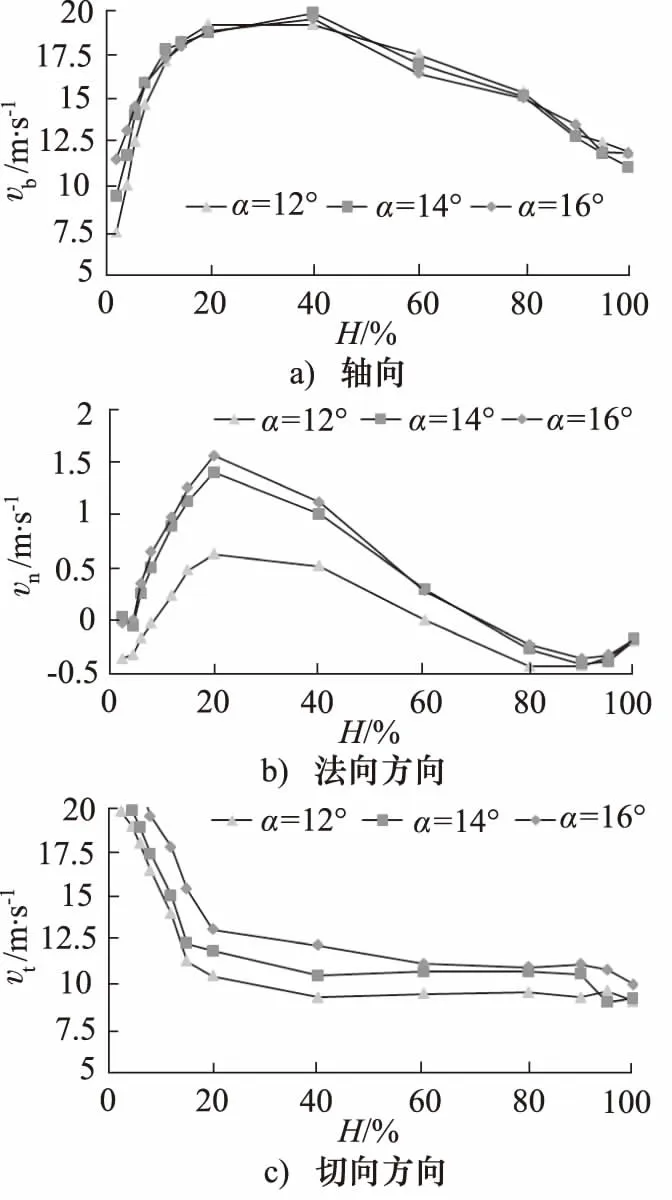
圖8 徑向葉高百分比與出口速度關系曲線

3 葉片風動性能優化

3.1 優化數學模型的構建

從風機葉片結構上分析，出口處的幾何角β更易于葉片壓力面流線分布的改變，這對于風機葉片的風動性能有著顯著的影響。若采用連續設計方法進行優化，將耗費大量的計算時間，因此，提出采用DOE(Design of Experiment)方法構建回歸模型[11]，并基于搜索算法得出風動性能最佳的出口處氣流角。根據仿真結果可知，14°滯后角葉片風動性能更優，因此以14°滯后角葉片為初始模型。風機葉片的等截面示意圖如圖9所示，被選取的變量參數如表1所示。為防止優化后的葉片結構發生畸變，保持c-c的弦長和e-e的弦長不變。

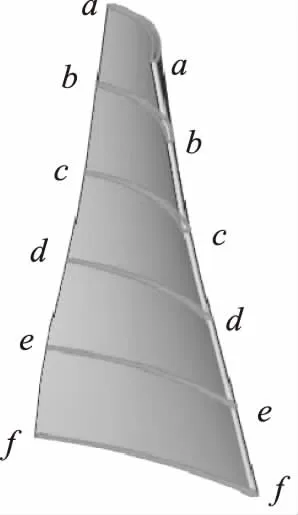
圖9 風機葉片的截面示意圖

表1 風機葉片原始參數

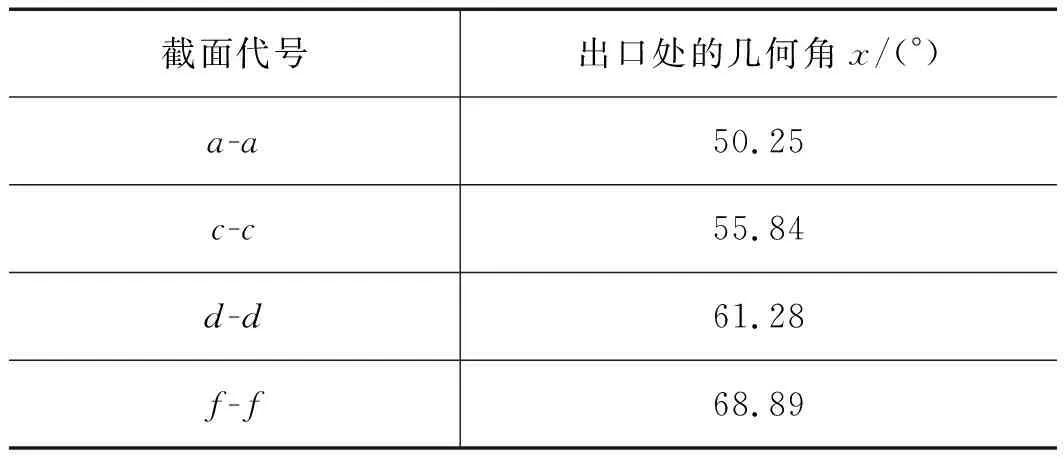
截面代號出口處的幾何角x/(°)a-a50.25c-c55.84d-d61.28f-f68.89

構建回歸模型之前，需要明確優化目標和設計變量。根據通風機的節能需要，該模型以全壓效率為優化目標，出口處的幾何角作為設計變量(各個變量浮動范圍為±20%)，并采用中心組合設計法[12]進行數據組合與匹配，最后根據不同的葉片結構計算全壓系數為0.34時的全壓效率。通過二次回歸分析，即可得出擬合函數。

在二次回歸條件下，優選最小二乘法進行數據處理[13]，最終可擬合出回歸函數為:

1.45x1x4-0.51x2x4+0.0017x3x4

(5)

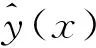
采用矩陣方式可將優化數學模型表示為:

max[y(X)]

(6)

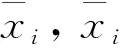
3.2 極值搜索算法

通過對優化數學模型的分析可知，風機葉片的優化問題在本質上為二次非線性極值搜索問題。在二次回歸分析條件下，各個截面的出口幾何角存在內在關聯。對于極值搜索算法，常見的有遺傳算法、模擬退火算法、粒子群優化算法、二次規劃算法等，其基本原理是一致的。由于回歸模型為二次多項式函數，約束條件相對明確，因此，模型優先選用二次規劃算法進行直接搜索[14]。優化數學模型的求解過程為迭代運算過程，全局收斂性是必須要滿足的[15]。若采用迭代步長系數αK來表示極值搜索過程中步長的變化，則迭代后的設計變量可表示為：

XK+1=XK+αKSK

(7)

式中，XK+1為迭代后的設計變量；XK為當前第K次搜索計算的設計變量；SK為當前第K次搜索計算迭代步長。

3.3 結果分析

采用Isight軟件[16]對式(6)進行求解，最終可得出極值所對應的設計變量，如表2所示。將優化后的結構進行參數化建模，采用CFD方法再次進行風動特性仿真，最終可得出優化前后的不同全壓系數下的全壓效率如圖10所示。可以看出：風機葉片在7種不同工況(全壓系數)下的全壓效率分別提升了11.6%，10.8%，9.32%，4.88%，10.3%，13.2%和 24.3%，可顯著降低電機在不同工作條件下的功耗。

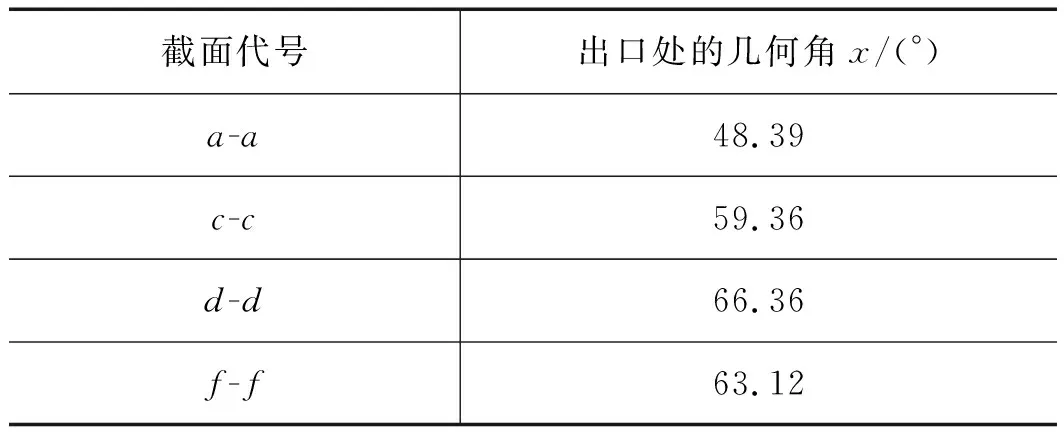
表2 風機葉片優化后參數

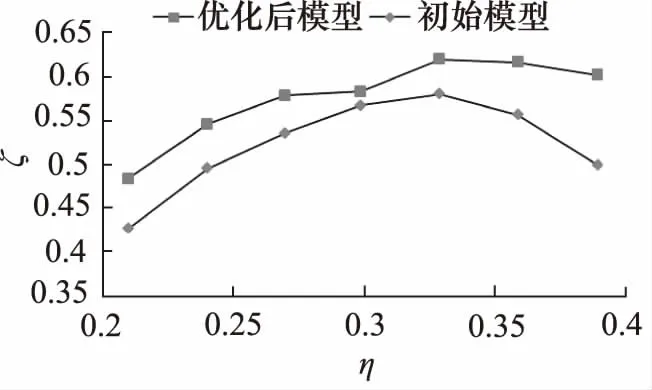
圖10 優化結果對比

4 結論

對于工業生產，合理機械結構設計能夠有效的實現節能降耗。本研究采用CFD方法分析了礦用軸流式通風機的風動特性，并基于DOE技術對風機葉片進行了優化，可得出以下結論：

(1) 在3種不同的滯后角(12°，14°和16°)條件下，14°滯后角葉片的在各種工況下的全壓效率均更高，壓力梯度更小，因此風動特性更優，可作為結構優化的初始模型；

(2) 為防止優化后的葉片結構發生畸變，以14°滯后角葉片部分截面出口處的幾何角作為設計變量構建回歸模型，進而確定出優化數學模型。基于二次規劃方法對該數學模型進行極值搜索，可在良好收斂性的條件下求解出葉片不同截面的最佳出口幾何角。通過整個優化設計，通風機葉片顯著地提升了全壓效率，這具有良好的經濟效益和社會效益。