帶攻角約束的高超聲速飛行器自適應反步控制器設計
董朝陽,劉 揚,王 青
(1. 北京航空航天大學航空科學與工程學院,北京 100191;2. 北京航空航天大學自動化科學與電氣工程學院,北京 100191)
0 引 言
高超聲速飛行器因其巨大的軍事和民用應用價值,受到廣泛關注[1]。而控制技術作為高超聲速飛行器的關鍵技術之一[2],給研究人員帶來了許多挑戰。
當前,高超聲速飛行器的控制設計已經取得了一定的研究成果。通過使用反步法[3],滑模控制[4-5],反饋線性化[6]等先進控制方法,高超聲速飛行器的非最小相位特性[3-4],強非線性[6],大不確定性[3-6]等問題得到了有效的處理。需要指出的是,上述控制器設計都旨在保證飛行器的高度以及速度的指令跟蹤性能,而忽視了對攻角的限制。然而,配備超燃沖壓發動機的高超聲速飛行器對攻角非常敏感[7],只有攻角位于適合的區間內時,超燃沖壓發動機才能正常工作,否則會帶來進氣道不啟動以及熱力壅塞等問題,嚴重降低飛行性能[8]。
針對攻角約束這一問題,傳統的方法是事先設計好一條標稱彈道,讓飛行器沿著彈道飛行。然后設計合適的控制器參數,使得整個飛行過程中滿足攻角約束要求。然而這樣的方法依賴離線設計,運算量大。文獻[9]提出的障礙函數近來被用于解決狀態約束問題。需要指出的是,障礙函數僅能保證虛擬指令的跟蹤誤差在預設范圍之內,比如文獻[10]中使用障礙函數對高度和速度跟蹤誤差進行限制。因此,為了限制系統狀態,還需保證虛擬指令的有界。文獻[11]使用基于障礙函數的方法解決了狀態約束問題,但是依賴于虛擬指令有界的假設。文獻[12]使用數值方法對虛擬指令上界進行估計解算,但是同時增大了計算負擔。文獻[13]通過在反步法構造障礙Lyapunov函數,并使用指令濾波器對虛擬指令限幅,解決了攻角約束問題。但是攻角約束是通過分別約束航跡傾角以及俯仰角實現的,設計流程較為復雜。此外,針對攻角約束的研究大多是考慮固定、對稱的攻角約束。但在實際情形中,發動機的理想工作條件往往是非對稱的,且是根據不同飛行狀態、任務而變化的。
本文提出了一種基于非對稱時變障礙Lyapunov函數[14]的自適應反步控制方法。不同于文獻[13]中的思路,本文直接對攻角進行約束,設計流程得到簡化。不同于文獻[12,15]對虛擬指令進行假設或估計的方法,本文使用光滑的類飽和函數對名義攻角指令進行限幅,避免了估計帶來的保守性與復雜性,并設計了輔助系統補償攻角指令限幅帶來的影響。此外,本文研究的攻角非對稱時變約束也更加符合實際情形。針對反步法中虛擬指令信號反復求導引起的“微分爆炸”問題,本文使用了滑模微分器進行估計。估計誤差與高超聲速飛行器模型中的不確定性與外擾一并視作集中干擾,通過自適應律進行估計與補償。
1 高超聲速飛行器模型
選取典型高超聲速飛行器縱向模型[6]
(1)
式中:V,h,γ,α,q分別表示速度、高度、航跡傾角、攻角、俯仰角速率;g為重力加速,Iyy為俯仰轉動慣量,m為飛行器質量;T,L,M,D分別為推力、升力、俯仰力矩、阻力,其具體表達式為:
(2)
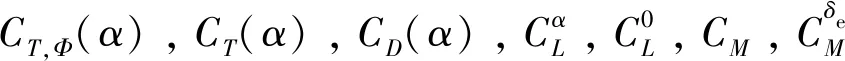
為了便于后續的控制器的設計與分析,引入下述引理。
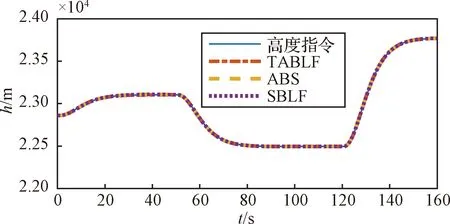
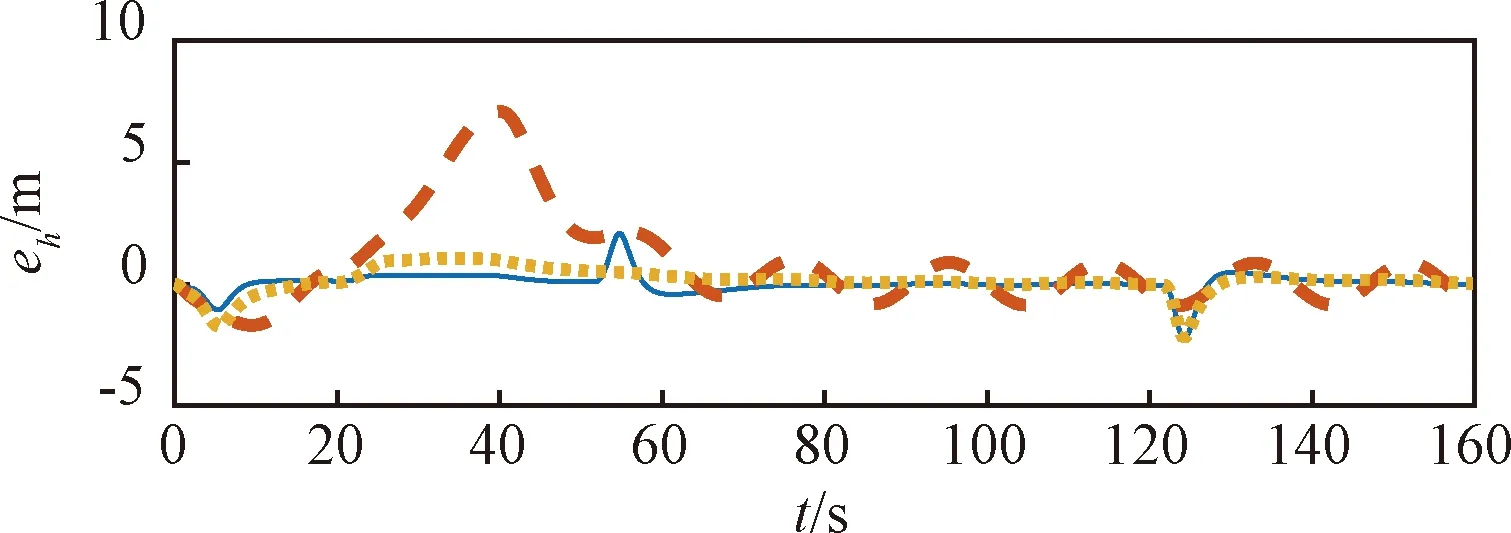
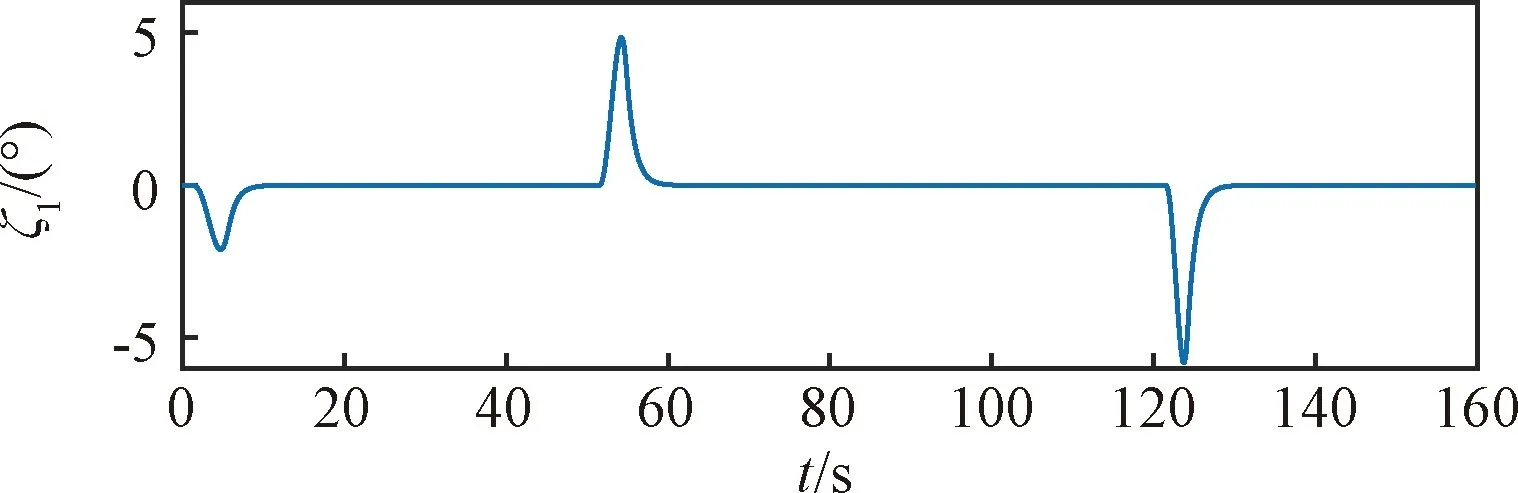
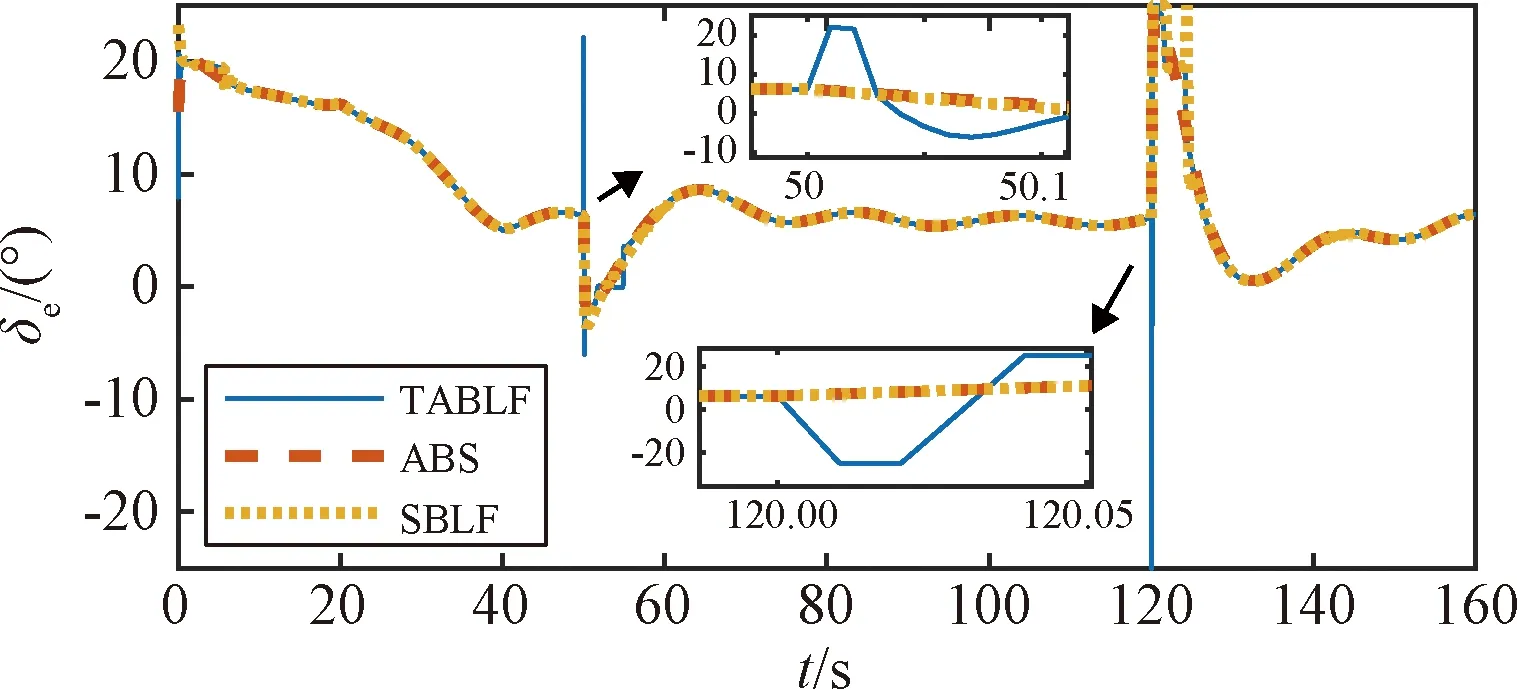
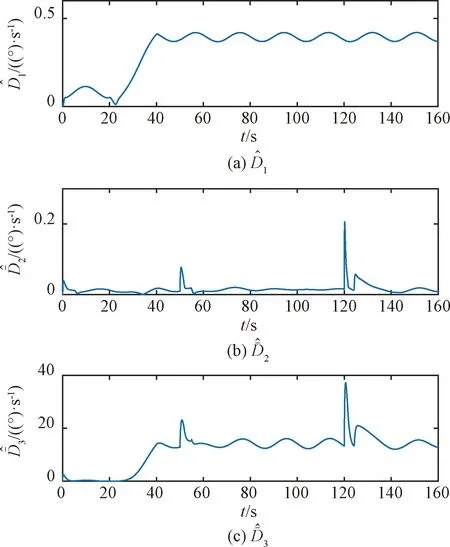
引理1[9]. 對于任意正數kb,如果有e∈R且|e| (3) 引理2[13]. 對于任意δ>0以及ε∈R,下列不等式成立: (4) 本文研究帶攻角約束的高超聲速飛行器控制問題。控制目標為:1)控制器能夠保證飛行器穩定,且能夠實現對指令信號的良好跟蹤;2)在飛行過程中,攻角滿足預設的時變非對稱攻角約束條件。 通過系統分解思想[16],高超聲速飛行器縱向模型可以分解為速度子系統與高度系統分別進行設計。本文研究重點是攻角狀態限制問題,而攻角狀態屬于高度子系統。另一方面,速度子系統階數較低,設計過程相對簡單。因此對速度子系統采用動態逆控制器以使得其保持穩定,設計與仿真省略,而將研究重心放在高階、需要考慮攻角約束的高度子系統中。 定義x1=γ,x2=α,x3=q,依據參考文獻[17],首先將航跡傾角跟蹤指令取為: (5) 式中:kh,khi為待設計的控制器參數;eh=h-hc為飛行器對高度指令信號hc的跟蹤誤差。 為了應用反步法,需要將原模型化為嚴反饋形式。為此,引入以下假設: 假設1[16]. 通常情況下Tsinα遠小于L,因此Tsinα項可以忽略。 注1.對于本文采用的模型數據[6],以及其適用的狀態量范圍(見文獻[6]中的表1),可以計算驗證該假設是成立的。 當滿足假設1時,高度子系統內環模型可以表示為: (6) 假設2.式(6)中的干擾di,i=1,2,3有界,且|di| 采用反步法對高度子系統每一通道進行設計。具體過程為: 1) 定義航跡傾角跟蹤誤差,則其導數為: (7) 為了實現攻角約束,采用光滑的類飽和函數對名義攻角指令x2r進行限幅,函數表達式為: x2f= (8) 式中:x2f是限幅后的輸出,滿足-Al 注2.相對于傳統飽和函數sat(·),式(8)可以保證x2f是光滑的,從而避免了求導運算中奇異現象的產生。 定義限幅攻角跟蹤誤差e2=x2-x2f和限幅造成的攻角指令誤差為:Δx2r=x2f-x2r。那么式(7)可以表示為: (9) 為了補償虛擬指令飽和對系統的影響,設計如下的輔助補償系統: (10) 進一步定義補償誤差信號z1=e1-ξ1,則其導數為: (11) 設計虛擬攻角指令x2r為: (12) (13) 式中:l1>0和b1>0為待設計的自適應律增益。 定義如下Lyapunov函數: (14) 對W1求導,并利用引理2化簡可得: (15) 2) 對限幅攻角的跟蹤誤差e2=x2-x2f求導: (16) (17) (18) 定義角速率指令跟蹤誤差e3=x3-x3r,設計虛擬俯仰角速率指令x3r為: (19) (20) 式中:β2>0為待設計的控制器參數,ka>0與kb>0為預先設定的e2的時變邊界: -ka(t) (21) ka與kb可以根據任務需求設定。 (22) 式中:l2>0和b2>0為待設計的自適應律增益。 將式(19)代入式(16),化簡可得: (23) 定義如下的時變非對稱對數障礙函數: (24) (25) 由ω(e2)的定義可知: (26) (27) 結合式(22)、(23)、(26)、(27)以及引理1和引理2,式(25)可進一步簡化為: (28) 3) 對角速率指令跟蹤誤差e3=x3-x3r求導可得: (29) (30) 式中:ζ31∈R與ζ32∈R為微分器的狀態量;r31>0與r32>0為待設計的參數;類似地,有 (31) 設計控制律u為: (32) (33) 式中:l3>0和b3>0為待設計的自適應律增益。 將式(32)、(33)代入式(29),化簡可得: (34) 進而定義Lyapunov函數: (35) (1-ω)τa]+g2e3[ωτb+(1-ω)τa]+ (36) 假設3.e2初值滿足初始時變約束,即-ka(0)<α(0) 定理1.對于高度子系統(6),在滿足假設1~3的前提下,采用式(12)、(19)、(32)所示的控制律以及式(13)、(22)、(33)所示的自適應律,則閉環系統滿足下述性質: 1)式(37)包含的所有誤差信號一致最終有界。 2)攻角x2始終位于指定的非對稱時變邊界內,即:-Al-ka(t) 證. 選取整個閉環子系統的Lyapunov函數為: WH=W1+W2+W3 (37) 對式(37)求導,代入式(15)、(28)、(36),化簡復雜的可消除項,可得: (38) 由于 (39) 式(38)可進一步化簡為: (40) 式中: κH=min{2k1,l1,2k2,l2,2k3,l3} 對式(40)兩邊同時積分,可得: (41) 由于-ka(0)<α(0) (42) -ka(t) (43) 又由于已知e2=x2-xf,且-Al -Al-ka(t) (44) 證畢。 本節通過對比仿真校驗所提出的控制器的有效性與優越性。所采用的模型幾何與氣動參數具體參見文獻[6]。飛行器的初始高度為22860 m;初始速度為1828.8 m/s;仿真中的高度指令信號的產生方式為將階躍指令 (45) 通過下述濾波器G(s) (46) 狀態反饋參數選取為:kh=1,khi=0.01,k1=1,k2=1,k3=20;自適應參數選取為:b1=20,σ1=0.01π/180,l1=1,b2=0.01,σ2=0.1π/180,l2=5,b3=100,σ3=π/180,l3=1;攻角邊界相關參數為:Au=3π/180,Al=2π/180,kb=e-0.07t,ka=0.5e-0.07t,p=0.95,β2=0.01;微分器參數選取為:r21=3,r22=3,r21=2,r21=10。 針對本文所提出的控制方案(以下記為TABLF),本文還采用了自適應反步法(以下記為ABS),以及文獻[13]中使用的非對稱非時變的障礙函數方法(以下記為SBLF)進行對比,用以說明本文方法的優勢。具體仿真結果見圖1~圖7。 圖1~圖2展示了指令跟蹤性能。由圖1可知,各控制器都能夠較好地跟蹤高度指令。從圖2可以看出,針對仿真中復雜、快時變的外部擾動,本文控制律的高度精度更高。這說明本文的自適應律對大幅值、快時變的干擾具有良好的估計與補償作用。 圖1 高度跟蹤曲線 圖2 高度跟蹤誤差曲線 圖3 攻角響應曲線 圖4 輔助狀態響應曲線 圖5 升降舵偏角 圖6 干擾上界的估計值 由圖3可知,本文提出的控制器可以保證攻角始終嚴格處于預設的時變非對稱區間之內。這得益于對時變非對稱的障礙函數與類飽和函數的綜合使用。而SBLF方法無法應對非對稱的約束,如圖3左下角與右下角子圖所示,采用SBLF方法的控制器越過了預設的攻角邊界。該方法也無法應對時變約束,如圖3左上角子圖所示,隨著攻角上界的縮小,SBLF的攻角曲線跨過了攻角上界。 由圖4可知,當名義攻角指令飽和時,輔助系統開始工作,用以補償飽和帶來的不利影響。當攻角指令退出飽和后,輔助狀態迅速回到0點。從圖5可以看出,當攻角在50 s以及120 s附近逼近邊界值時,本文控制器迅速產生大的反向舵偏,以避免攻角超出邊界。 圖6為干擾上界的估計曲線,可以看到干擾估計值快速變化以準確估計幅值不斷變化的集中擾動。 綜上所述,仿真結果校驗了本文提出方法的有效性。具體而言,首先在大幅值、快時變干擾下仍然能夠準確跟蹤指令信號。其次,飛行過程中,攻角的非對稱時變約束始終能夠得到滿足。 對于帶攻角約束的高超聲速飛行器,本文提出了一種新型的非線性自適應控制器。通過分別使用類飽和函數約束攻角指令,障礙函數約束攻角指令跟蹤誤差,實現了對飛行器攻角的時變非對稱約束。并構造了輔助系統用以補償攻角指令飽和帶來的影響。飛行器受到的參數不確定性、擾動以及指令信號導數的估計誤差被統一視作集中干擾,通過自適應律進行在線估計補償。仿真結果表明,本文提出的控制器可以保證良好的跟蹤性能,并且攻角始終滿足約束條件。2 控制器設計
2.1 控制目標
2.2 模型簡化

2.3 高度控制器設計
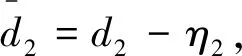
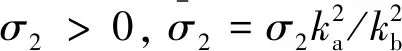
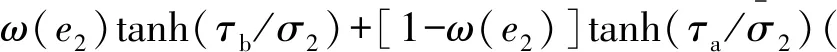
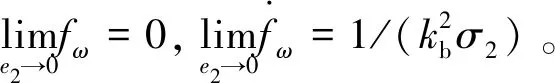
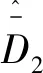
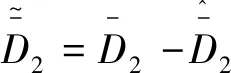
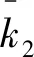
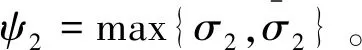
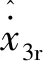
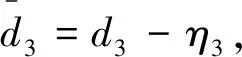
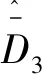
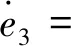
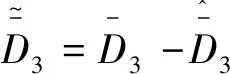
2.4 穩定性分析
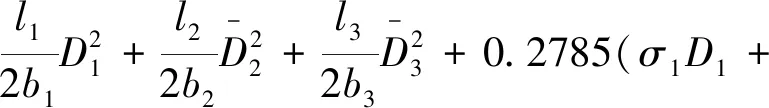
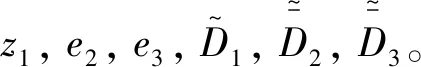

3 仿真校驗
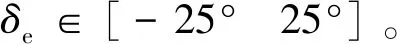

4 結 論

