基于隱式溫度修正的二維熱線風速儀校準方法

張 軍, 張俊龍, 雷紅勝, 趙維明, Con. Doolan

(1. 中國空氣動力研究與發展中心 氣動噪聲控制重點實驗室, 四川 綿陽 621050；2. 中國空氣動力研究與發展中心 結冰與防除冰重點實驗室, 四川 綿陽 621050 3. 澳大利亞新南威爾士大學 機械與制造工程學院, 悉尼 2052)

0 引 言

由于熱線風速儀具有很高的時間和空間分辨率，故熱線比粒子圖像測速(PIV)、激光多普勒儀(LDV)等更適合湍流流場的測量[1-3]。熱線風速儀的工作原理為：通過儀器的內置電路(惠斯通電橋)加熱微型金屬絲，氣體流動帶走金屬絲上的熱量從而引起測量電阻的變化，惠斯通電橋對其進行補償，補償電阻的變化即反應了風速的變化[4-5]。熱線風速儀主要有恒溫(CTA)、恒壓(CVA)和恒流(CCA)三種工作模式。根據熱線絲的幾何形狀不同，熱線探頭有多種分類，并覆蓋了從一維到三維流場的測量范圍。本文主要研究恒溫模式下的二維熱線風速測量。為了得到真實的風速，需要先建立起熱線電壓與風速之間的校準關系，再將測量得到的電壓值換算成風速值。一般情況下，熱線的校準和測量過程是獨立進行的，環境溫度的變化將會給測量結果帶來誤差[6-8]。

假設環境溫度變化足夠小、氣體的物理性質保持不變，Westphal[9]基于熱線的溫度系數、過熱比、以及校準/測量之間的環境溫度差，最早提出了一種溫度效應修正的簡化公式。Brunn[10]隨后提出了一種改進的熱線溫度修正工程化方法，并在實際測量中得到了廣泛的使用。但是當環境溫度在短時間內變化較大或流體性質發生變化時，例如對于無冷卻設備的低速回流式風洞、結冰風洞或增壓風洞中的流場測量，Westphal 和Brunn的修正方法會帶來明顯誤差[11]。Cukurel[12]等考慮了氣體的可壓縮性，提出了一種用于測量跨聲速噴流的二維熱線校準方法。然而，Cukurel等沒有考慮溫度效應修正，故無法對諸如發動機熱噴流之類的流場進行測量。Marcus[13]研究了強制對流中的熱傳遞過程，提出了一種無量綱化的熱線溫度效應修正方法，并在高雷諾數氣流的流場測量中得到了應用。

本文從熱線風速儀的工作原理出發，結合氣體物理參數之間的關系，提出了一種新的二維熱線校準方法。該方法將溫度效應修正隱式的包含在熱線校準公式中，突破了傳統方法對溫度變化范圍的限制，同時不受高壓、低溫等試驗條件下氣體物理參數變化的影響。本文的研究內容安排如下：第一節給出了二維熱線校準的理論方法，并對隱式溫度效應修正方法進行了闡述；第二節，對本文提出的校準方法進行了實驗驗證；第三節，對全文進行了總結。通過本文研究，以期提高二維熱線的測量精度和拓展熱線風速儀的應用范圍。

1 理論方法

根據Brunn提出的方法[10]，熱線測量的輸出電壓可以根據下式進行修正：

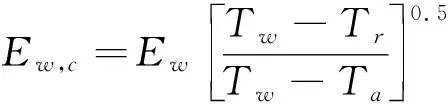
(1)

其中：Ewc、Ew分別表示經過修正后的結果和原始測量數據；Tw表示熱線的工作溫度；Ta表示環境溫度；Tr表示熱線校準時的環境溫度。在標準大氣條件下，式(1)是一個非常有用的經驗修正公式。根據Jorgensen的研究結果[6]，式(1)應在環境溫度變化±5 ℃范圍內使用。如果溫度變化過大，則應多次重復進行校準。下文我們將推導一種新的用于二維熱線風速測量的溫度效應修正方法，圖1是二維熱線風速儀探針示意圖。

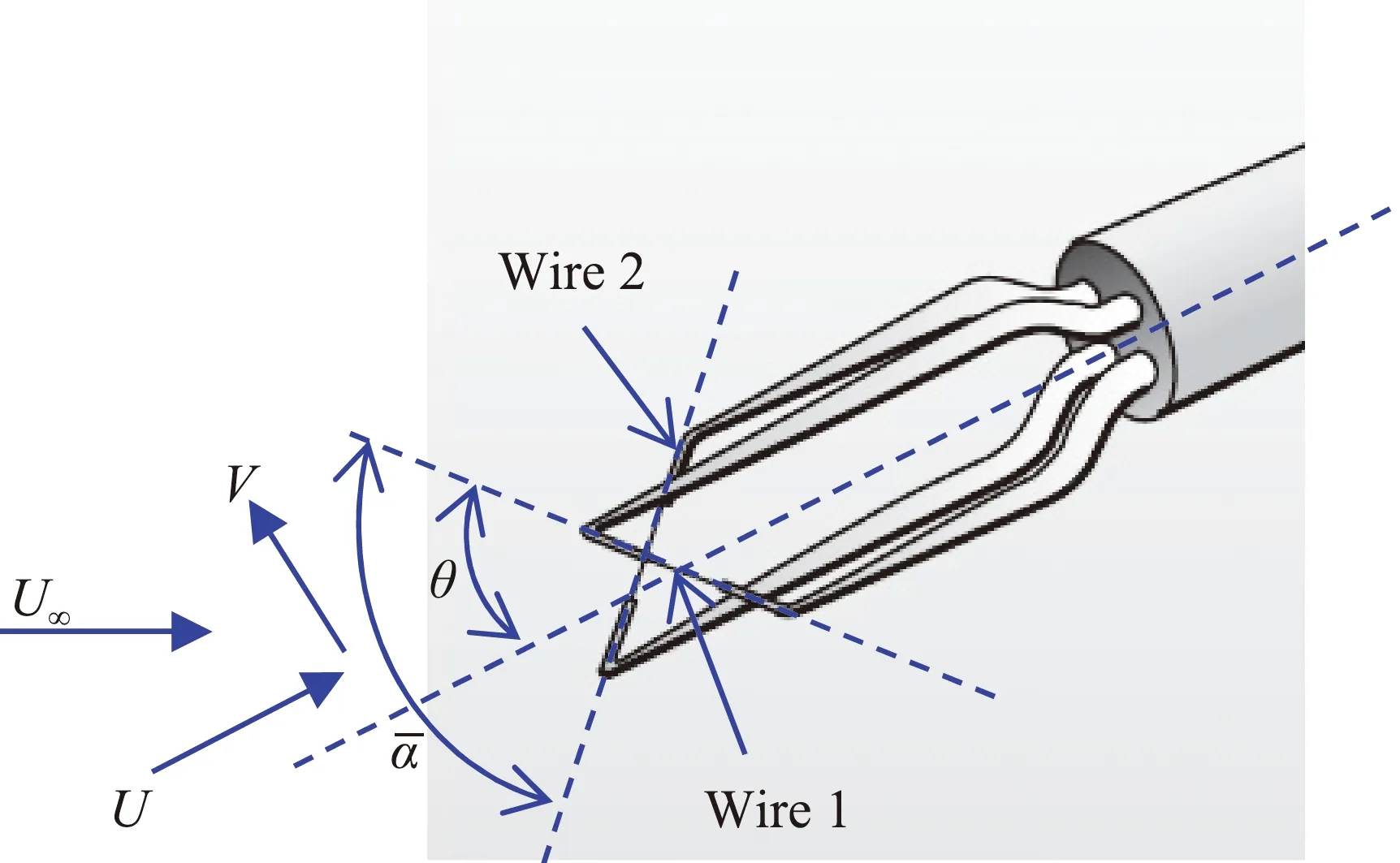
圖1 二維熱線風速儀探針示意圖[14]Fig.1 Schematic of a cross-hotwire probe

試驗測量過程中，熱線暴露在氣流當中，熱線上的能量損失主要有三種方式：對流、輻射和傳導。縱橫比(長度與直徑之比)大于200的熱線主要以自由對流的方式耗散能量[15]。大部分用于科學研究的熱線的縱橫比大于200，故以下的分析中只考慮強制對流效應引起的能量損失。對于在恒溫模式下工作的熱線風速儀，惠斯通電橋使熱線的溫度或電阻值保持恒定。強制對流效應在熱線電阻上產生的焦耳熱可以用以下式表示：

(2)

其中，Iw和E分別表示熱線上的電流和電壓；Rw、d和L分別表示電阻、熱線絲的直徑和長度；h=Nu·κ/d表示對流熱傳導系數，Nu表示努塞爾數，κ是氣體的導熱系數。根據Collis和Williams的研究結果[16]，氣體的努塞爾數Nu與雷諾數Re之間滿足如下關系：

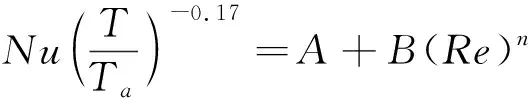
(3)

式中：T表示氣流的溫度；Ta表示參考溫度；A、B和n是經驗常數，通過實驗確定。對于典型的微米直徑的熱線，式(3)在雷諾數Re=0.01～140范圍內是成立的。根據式(3)，式(2)可以改寫為：

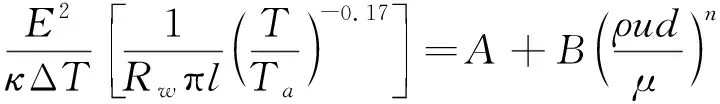
(4)

其中：ΔT=Tw-Ta表示熱線與周圍氣的溫度差，ρ和μ分別表示氣體的密度和運動粘滯系數。由于式(4)方括號中的量近似為常數，故可進一步簡化為：

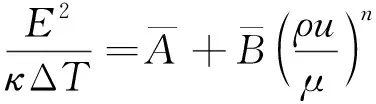
(5)

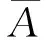
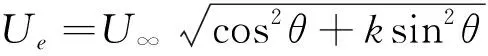
(6)

式中：U∞表示自由來流速度；k表示冷卻常數(與順氣流方向的氣流速度相關)；θ定義為氣流方向與熱線探針軸線之間的夾角，θ為正表示順時針方向。 聯立方程(2)、(3)和(4)，可得到氣流速度和熱線輸出電壓之間的關系式:

(7)

其中：κ、ρ和μ等氣體物理參數與溫度的變化密切相關。根據電壓E、自由來流速度U∞和傾角θ的校準數據，通過方程(5)進行曲線擬合，可以給出A、B、n和k的校準值。在一定的溫度和壓力范圍內，氣體物理參數κ、ρ和μ的值可以通過下面的式子給出：

式中:p表示大氣壓力，T表示熱線絲周圍氣體的溫度。根據二維熱線的角度和速度校準結果，結合試驗測量得到的電壓數據，使用Brunn給出方法可以得到二維流速分量Uc和Vc的估計值[10]：

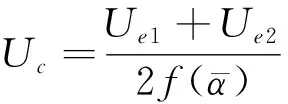
(9)

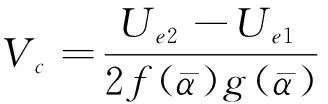
(10)

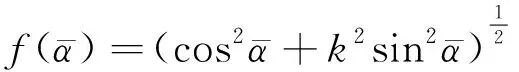
(11)

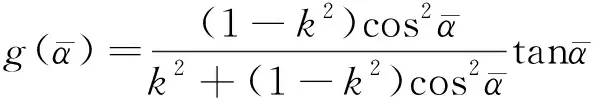
(12)

2 實驗研究

2.1 二維熱線校準

本文使用TSI公司的TSI1129校準器對一只新修復的 TSI二維熱線探針進行了校準。在校準過程中，使用Dantec54N80常溫風速儀記錄熱線的電壓模擬量輸出，并用NI-9219 數據卡將模擬量轉換為數值量。設定CTA的過熱比時，需要使用萬用表測量熱線探針、引線、支架和電纜的電阻值，然后將其作為參考值來計算過熱比。實驗過程中，數采卡的采樣率設置為50 Hz (校準)，采樣時間是20 s。 在標準大氣壓條件下，平均環境溫度分別為 21 ℃和25 ℃時，實驗測量得到了兩個校準數據集。其中一個數據集包含11個傾斜角度(從-30°到30°，步長為6°)和每個角度測點上包含30個流速值(從5 m/s到80 m/s)。另一個數據集包含相同的角度測量點和一半的流速測量點。

圖2給出了二維熱線中的2#熱線絲在零度傾斜角下的速度校準結果。由于結果非常類相似，文中沒有重復給出該熱線絲在其它俯仰角下的結果或1#熱線絲的結果。圖中的結果是由相同的熱線絲在不同溫度下(21 ℃和25 ℃)測量得到的。如圖2(a)所示，如果不進行溫度修正，同一條熱線在不同溫度下的校準結果是不同的，特別是在流動速度較高的情況下更是如此。其對測量結果的影響主要表現在，通過電壓輸出和校準結果得到的流速的測量值將偏離真實值。取參考溫度Tr=25 ℃，使用Brunn的方法或本方法修正21℃下獲得的校準數據，可以發現兩次校準得到的曲線完全重疊(見圖2(b)和圖2(c))。這表明兩種方法都可以有效糾正溫度效應。但是Brunn的方法要求溫度變化小于幾度，而本文提出的方法則沒有這個限制。

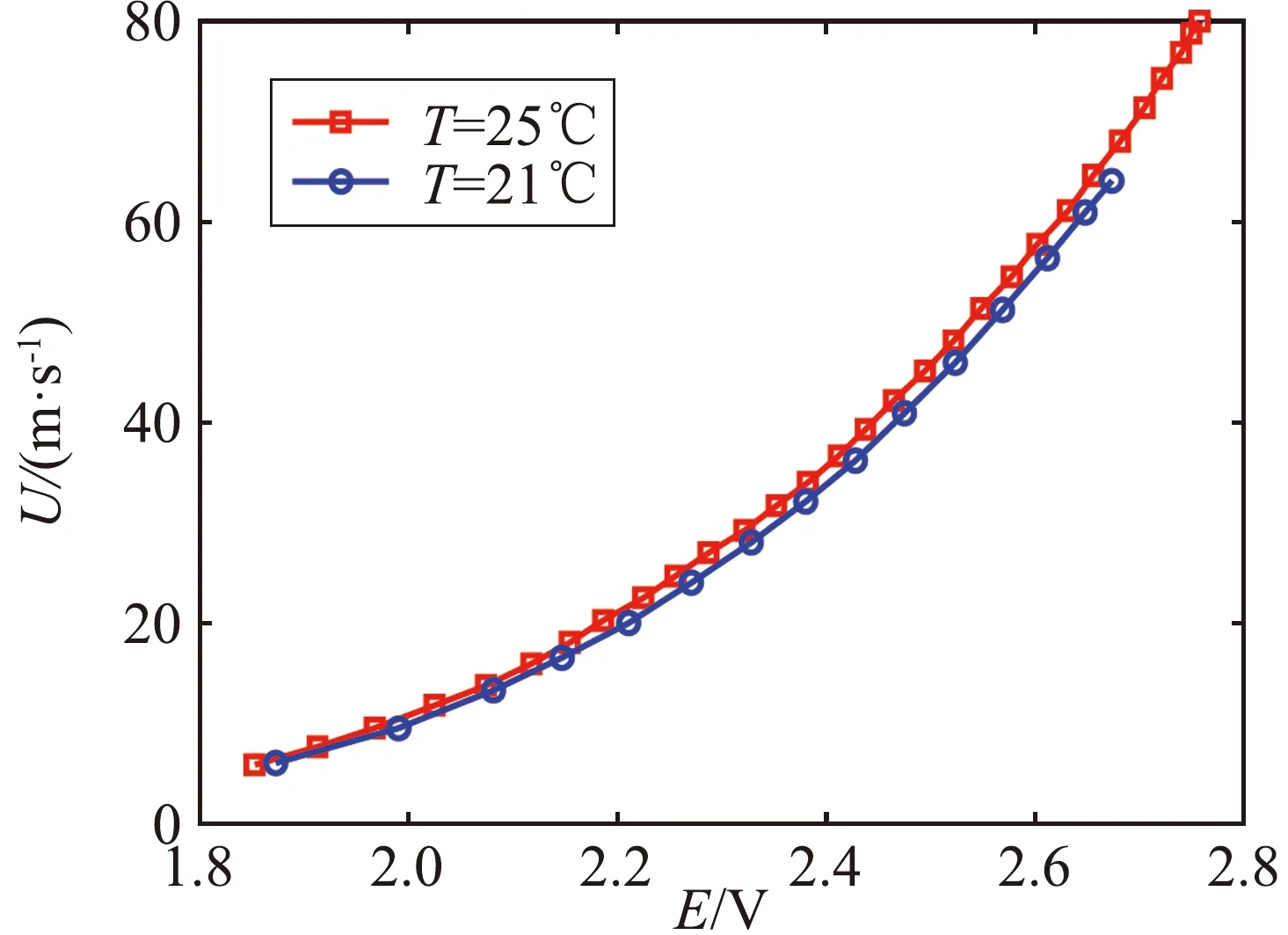
(a) 原始數據

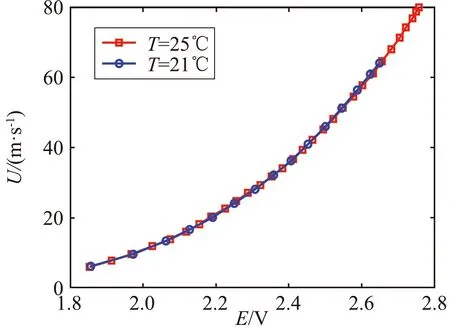
(b) Brunn方法

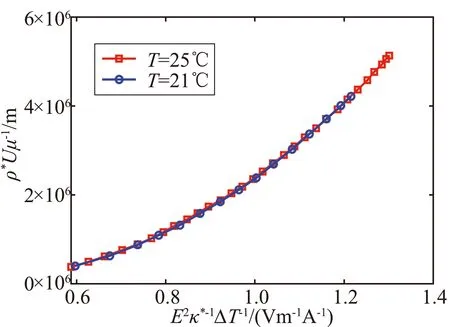
(c) 現方法

在高雷諾數條件下，氣體的物理性質對溫度變化敏感，使用Brunn的方法將會帶來明顯的誤差，下文將進行說明。

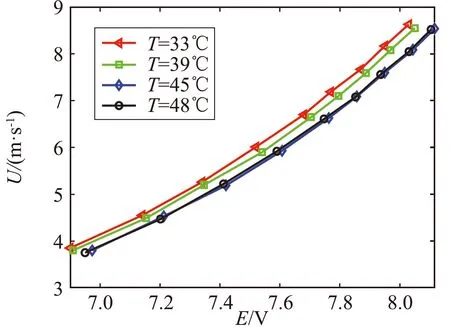
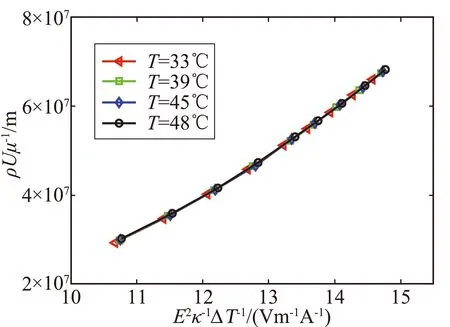
圖3(a)中給出了Marcus 和Smits[13]在普林斯頓高雷諾數測試設備(HRTF)上對熱線校準獲得的原始數據。如果不開冷卻設備，空氣的溫度在短時間內可以升高10 ℃以上。在高氣壓條件下，空氣的密度、熱傳導系數和動力粘滯系數等必須相應地進行修正。從圖3(a)中可以看出，熱線的輸出電壓隨氣流溫度變化而改變，使用 Brunn的方法進行修正后校準曲線仍然不重合(T=33 ℃被取為參考值，見圖3(b))。而使用本文提出的方法后，所有校準數據完全重疊(見圖3(c))，這表明溫度變化對熱線測量的影響可以通過本方法被準確地修正。

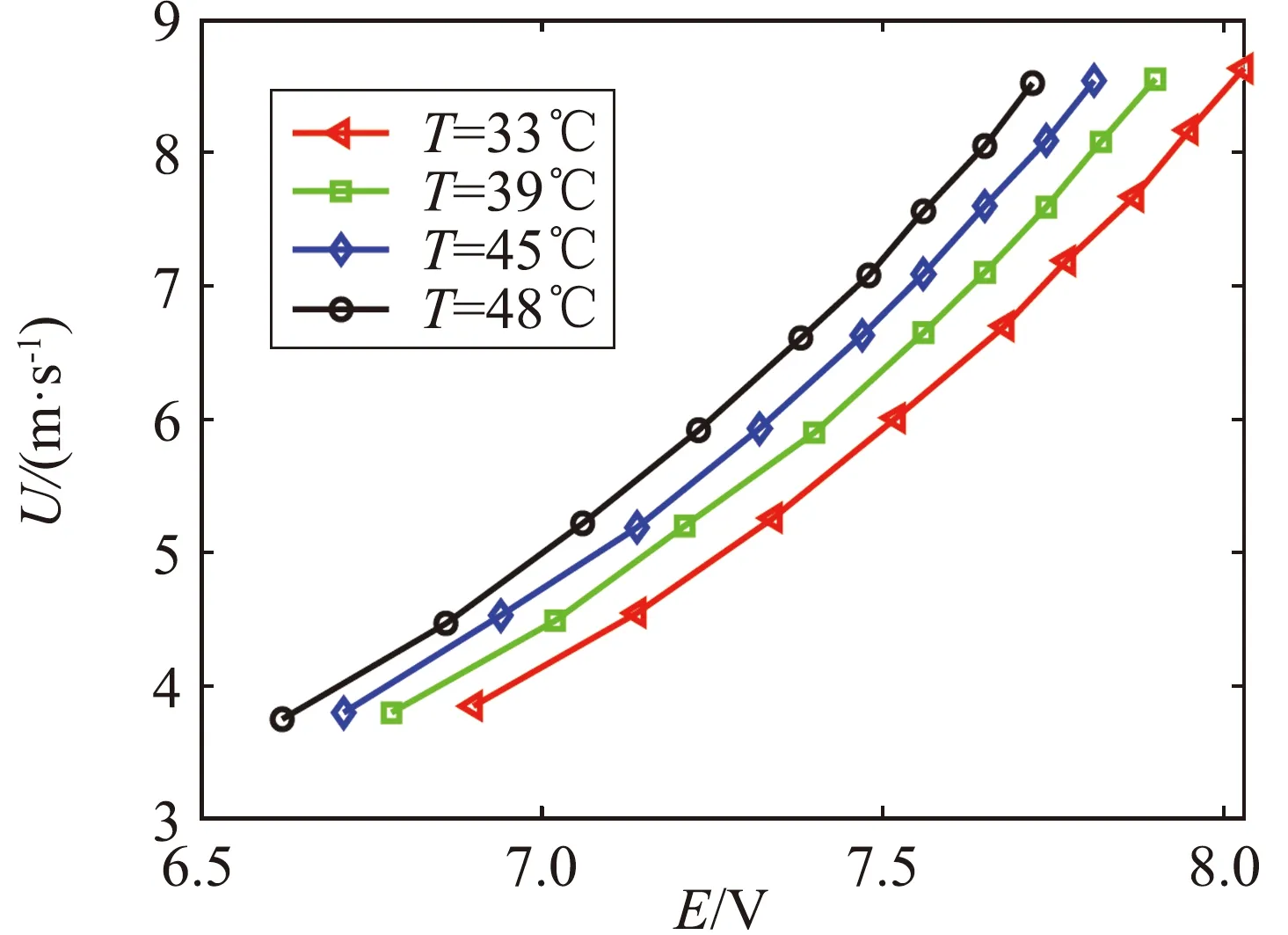
(a) 原始數據

(b) Brunn方法

(c) 現方法

表1給出了TSI二維熱線的校準常數A、B、n和k的值，其中k代表二維熱線的角度校準結果。校準過程中的平環境溫度為25 ℃，溫度變化小于1 ℃。上述校準系數是根據式(5)，采用曲面擬合的方法得到的，擬合的置信因子R2總是大于0.99。根據表中的結果，兩種溫度修正方法得到的k值大致相等，同時是否進行溫度修正對k值的影響不明顯。這表明冷卻常數k主要由熱線的幾何形狀決定，溫度變化對二維熱線的角度校準沒有影響。

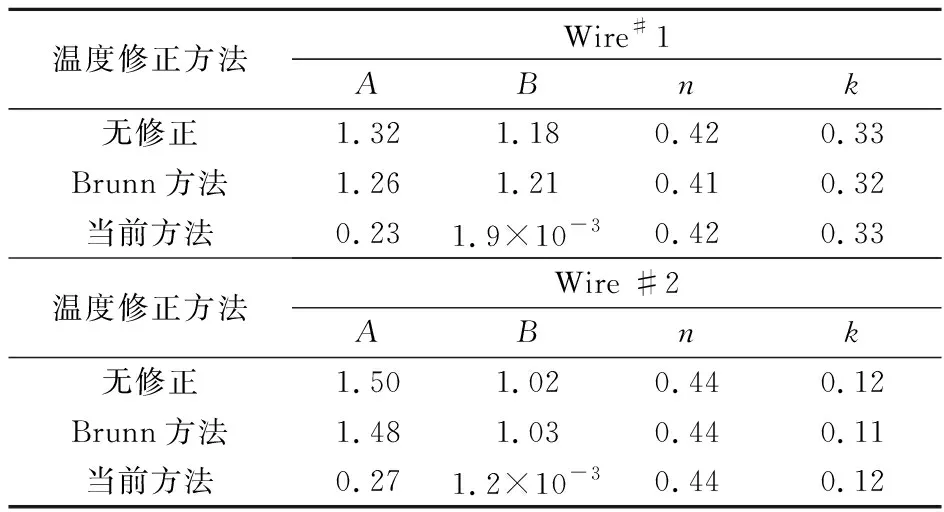
表1 TSI二維熱線的角度校準結果，25 ℃Table 1 TSI cross-hotwire calibration results, 25 ℃

2.2 基于二維熱線風速儀的風洞流場測量

新南威爾士大學的UAT聲學風洞是一座開口直流式風洞，風洞噴口尺寸為0.46 m×0.46 m[18]。2018年，UAT風洞進行了升級改造。風洞升級完成后，可以獲得更高的風速，試驗段的流場品質也有了較大的提升。風洞正式投入運營之前，使用二維熱線風速儀進行了流場測試。

圖4給出了UAT風洞的流場測量結果。熱線測量結果的準確性使用皮托管進行了驗證。 校準和試驗測量之間的溫度差為3 ℃。 如果沒有進行溫度校正，熱線測量結果將偏離皮托管的測量數據，最大相對誤差可以達到5%(40 m/s，見圖4(a))。根據本文提出的方法進行溫度修正之后，熱線數據與皮托管的數據之間非常吻合。圖4(b)給出了40 m/s 風速條件下的風洞自由射流的速度剖面曲線，其中y/D=0表示噴口中心線，y/D=-0.5表示風洞噴口邊緣線(剪切層的位置)，D=0.46 m表示風洞噴口的尺寸。從圖上可以清楚地區分射流的核心區和混合區。圖4(c)和圖4(d)，給出了沿流向幾個不同位置的軸向(u′)和橫向(v′) 湍流功率譜(測點位于剪切層的中心位置，即y/D=-0.5)。湍流譜可以根據曲線斜率值被劃分為三個區域：大的渦流區，慣性副區，能量耗散區；該測量結果與前人的實驗結果是一致的[19]。

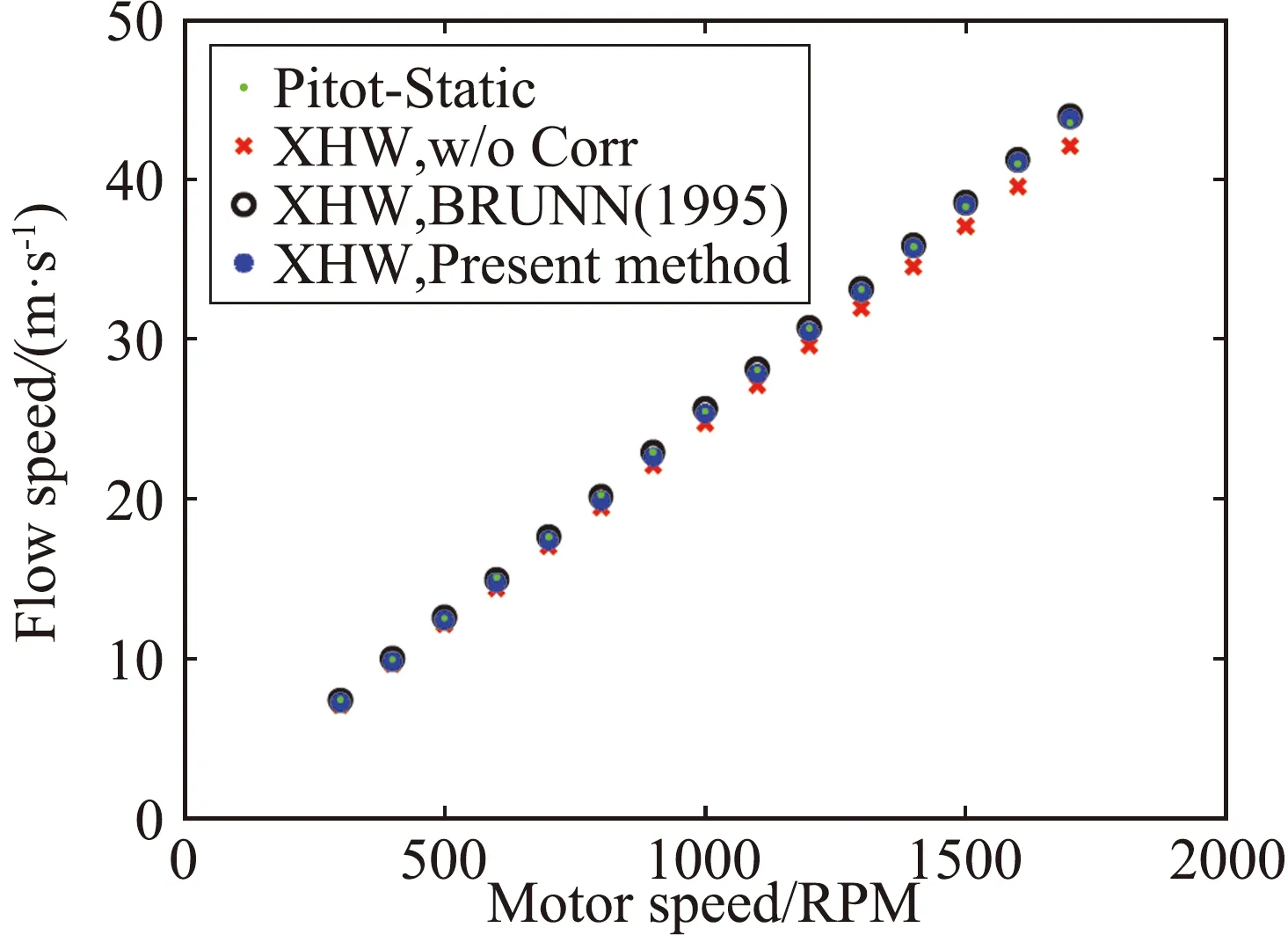
(a) 皮托管與熱線結果對比

(d) 橫向湍流功率譜

3 結 論

熱線風速儀主要用于湍流流場測量，熱線測量的主要誤差來源是由環境溫度變化導致的熱線校準參數的變化。通常使用的Brunn溫度效應修正方法在溫度變化較大的情況下會帶來明顯的誤差。本文經過理論推導，提出了一種新的用于二維熱線風速儀校準的溫度修正方法，并開展了熱線校準實驗研究，結果表明：1) 當環境溫度變化在4 ℃以內時，本文提出的方法與Brunn方法的測量精度相當；2) 當環境溫度變化大于4 ℃時，本文提出的方法的測量精度遠高于Brunn方法。 與傳統的Brunn方法相比，本文提出的方法可大大減少熱線測量過程中的校準次數，對提高試驗的質量和效率有意義。需要說明的是，現階段受實驗條件限制，本文沒有開展溫度變化范圍較大條件下的湍流流場測量。待條件成熟后，作者將繼續開展相關的研究工作。

致謝:本文的實驗部分工作是在澳大利亞新南威爾士大學做訪問研究員期間完成的，感謝國家留學基金委(CSC)的資助，感謝Con. Doolan教授課題組提供實驗設備支持。