二階隨機占優約束下考慮訂購能力的多產品報童問題

付永彬, 孫海琳

(南京師范大學數學科學學院，南京 210023)

1 引言

經典報童問題即單周期庫存問題(Single-Period Problem, SPP)，其研究對象為生命周期短、易腐蝕、訂貨機會只有一次的產品，主要研究其訂貨問題和庫存決策問題，是供應鏈管理中最重要的模型之一．隨著生產和銷售的復雜化，學者們將經典的報童模型擴展為多產品報童模型(Multi-Product Newsvendor Problem, MPNP)，通過在各種產品之間合理分配有限的資源，使報童總的期望利潤最大或損失最小．

Whitin[1]首次建立了受價格影響的報童模型；Khouja[2]對報童問題的擴展模型做了分類說明；Mitra[3]以單產品報童問題為背景，將產品的殘值、清倉價格均視為決策變量，分別就季節性需求和季末需求是否外生和隨機建立了三個模型．Kyparisis 和Koulamas[4]分析了非負線性可加需求對單產品報童問題訂價敏感度的影響．Wu 等[5]研究了單產品的報童博弈問題，提出了兩種數量競爭的需求分割規則，包括需求分配比例規則和需求再分配規則．Wang 等[6]考慮單產品報童模型，分別對風險中性和風險厭惡下隨機供應對最優訂貨量的影響進行了研究．Mohammad 和Shokri[7]考慮風險厭惡條件下，以CVaR 為風險度量的多產品選擇問題．Farahat 和Leeb[8]考慮在一般選擇規范下，即包含替代、互補、多單位訂購、缺貨、庫存等情形，建立了客戶的對產品選擇模型．Shi 等[9]討論了供應商數量折扣合同下，多產品多約束的聯合訂價及最優訂購量問題；Murray 等[10]主要研究在資源能力有限條件下，報童的多產品訂價問題；周繼祥[11]分別討論了訂貨無約束下、供應商隨機生產約束下、資金約束下報童模型的顯式解；陳杰等[12]對具有多元馬氏需求特征的多產品庫存報童模型的優化問題進行了探討；Ma 等[13]針對需求可替代的多產品報童問題研究了其最優產品組合及最優訂貨量的聯合決策問題．

在現實中大多數零售商是風險厭惡的，針對需求的不確定性所帶來的風險，許多學者采用不同的模型進行研究．張艷霞等[14]對定常風險下具有不同風險偏好組合決策者的報童問題進行了風險分析；簡惠云和許民利[15]針對風險規避和風險偏愛兩種情況，分別建立不同訂購量和風險水平下的條件風險值模型，考慮缺貨成本，在一定條件下，得到任意風險水平下的VaR 解析表達式；周艷菊等[16]運用前景理論，針對需求不確定條件下的兩產品訂貨問題進行了分析；Zhang 等[17]分別采用VaR 和CVaR 對單周期和多周期報童問題進行建模．

隨機占優(Stochastic Dominance, SD)是風險管理的一種理論方法，已經廣泛用于經濟、管理學和金融學領域．Hadar 和Russel[18]首次提出隨機占優的理念；Fishburn[19]整理出隨機占優理論，并將隨機占優理論應用于組合投資問題．作為一種重要的隨機占優方法，SSD 可用來描述風險規避型投資者的行為．Dentcheva 和Ruszczyski[20]首次提出帶有SSD 約束的隨機優化模型，他們通過引入新的變量把該問題重新構造成一個線性約束優化問題；Dentcheva 和Ruszczyski[21]分析了該問題的最優性與對偶性等問題；Homem-De-Mello 和Mehrotra[22]結合了割曲面算法與樣本均值逼近(SAA)方法來求解帶SSD 約束的隨機優化問題；Sun 等[23]用光滑的罰函數SAA 方法來求解該問題；Rudolf 和Ruszczyski[24]，Fbin 等[25]分別采用切平面算法來求解帶SSD 約束的隨機優化問題；Sun 等[26]進一步將切平面法改進，更適宜解決大量非線性約束的凸優化問題；Yang 等[27]將SSD 應用于供應鏈系統，研究了多制造商多零售商之間最大化利潤的交叉訂購與定價問題；羅曉琴等[28]將二階隨機占優理論應用于保險資金資產組合優化；吳敏等[29]考慮偏度因素，建立了SSD 約束下最大化組合收益率偏度的投資組合優化模型；張宏偉等[30]采用SSD 理論對投資組合問題進行建模，并通過遺傳算法求解；楊柳和申飛飛[31]通過引入交易費用函數，建立帶有SSD 約束的投資組合風險控制模型．

在隨機規劃問題中，隨機變量未知．SAA 是一種經典的、實用的估計隨機變量分布的方法．該方法利用隨機變量的經驗分布去近似其真實分布，有著深厚的理論基礎、良好的可操作性和應用價值，在學術界已被廣泛論證和使用[32]．進一步，SAA 在報童問題中也是常用的方法[17]，部分原因是報童問題的零售商可以比較方便地根據以往銷售情況獲得產品需求的各項信息作為SAA 問題的樣本．這樣的樣本具有真實、利用率高等優勢．

多產品報童問題涉及庫存管理、風險管理、供應鏈協調等多個領域．隨著風險控制領域的不斷發展，將新的風險測度應用于報童模型既能體現新的風險測度的優越性，又能對經典模型帶來新的思路和啟發．本文建立了帶有隨機二階占優約束的多產品報童模型，主要貢獻如下：

1) 本文首次將SSD 與報童問題相結合，建立了帶有SSD 約束的多產品報童模型，考慮了在SSD 約束及訂購能力約束下零售商的最優訂購策略；

2) 本文采用SAA 方法對帶有SSD 約束的多產品報童模型進行逼近，并對SAA 逼近問題進行收斂性分析；繼而采用切平面法[26]對SAA 問題進行求解．數值實驗的結果既驗證了SAA 問題的收斂性，同時又說明了SSD 模型的優越性．

2 SSD約束下的報童模型

2.1 模型介紹及參數設定

鑒于零售商總是同時訂購和銷售多種產品，本文考慮對零售商在單周期內對多種產品銷售的報童問題進行建模．現實中零售商往往不會把所有資金都應用于產品訂購，或者出現零售商訂購能力有限，或資本難以周轉等其他情形，所以本文設定訂購能力約束；同時又借助SSD 來規避風險．假設各種產品之間互不相關，不考慮訂貨提前期且貨源充足．產品的零售價格由市場決定，為已知量；訂購價格和殘值由供應商決定，為已知量；產品市場需求為隨機變量．零售商需要在銷售季到來之初，確定各種產品的訂購量，以期獲得最大利潤．

設共有M 種產品，對第m(m=1,2,··· ,M)種產品：訂購量為xm, xm∈R+；市場需求為Dm, Dm: ? → Ξm是定義在概率空間(?,F,P)上的隨機變量，分別為單位銷售價格、單位訂購價格、單位殘值，且pm>cm>vm>0．令

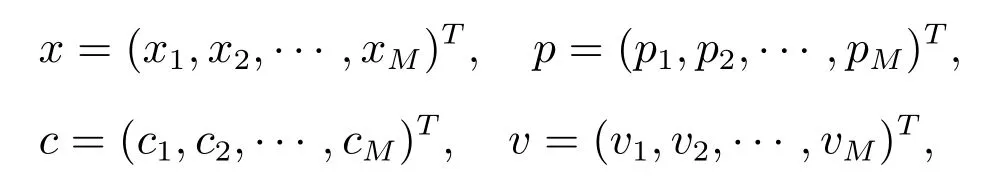
則在當期對于第m 種產品，零售商的銷售量為min(xm,Dm)；庫存量為xm?min(xm,Dm)；銷售收入為pmmin(xm,Dm)；未賣出產品的殘值為vm[xm?min(xm,Dm)]；訂購成本為cmxm．所以第m 種產品的利潤為

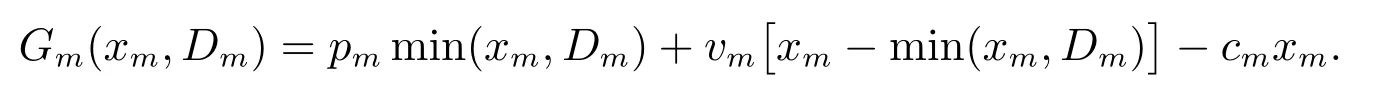
M 種產品的總利潤為

由于min(a,b)=a ?(a ?b)+，其中(a ?b)+=max(a ? b,0)，上式可化簡為

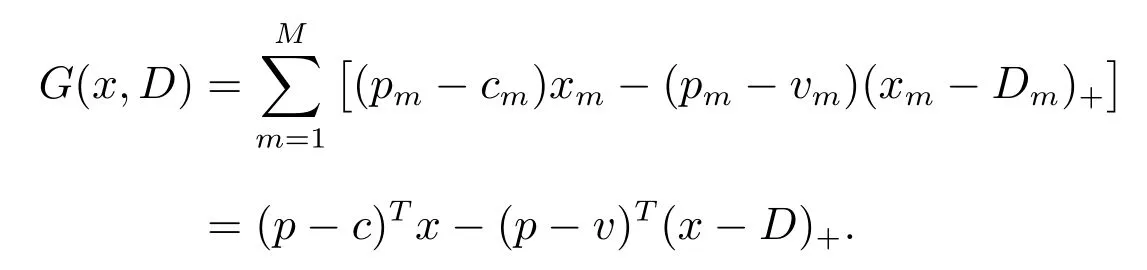
設J(x,D)=?G(x,D)表示損失函數．在訂購能力約束下最小化期望損失的報童模型為

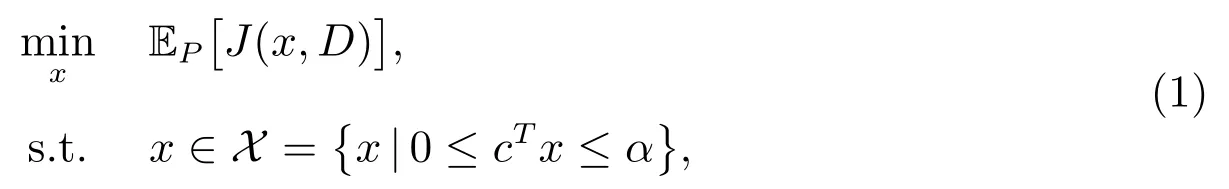
其中α 為常數，該模型也稱作風險中性模型．

2.2 SSD約束下的報童模型

在現實中大部分投資者是風險厭惡的，而問題(1)未考慮風險因素對報童的影響．如前文所述SSD 可用來描述風險規避型投資者的行為，因此，本節引入SSD 約束，構建帶有SSD 約束的風險規避型報童模型．

首先介紹SSD 的定義：設X(ω), Y(ω)分別為隨機變量ω 的兩個函數，其累積分布函數分別為FX(ω)(η)和FY(ω)(η)，即FX(ω)(η)=P(X(ω)≤ η)．令若滿足

則稱X(ω)一階隨機占優于Y(ω)，記作X(ω)?1Y(ω)．令

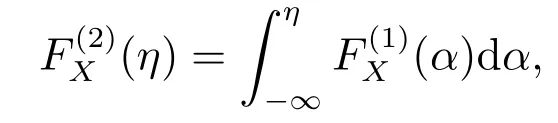
若滿足

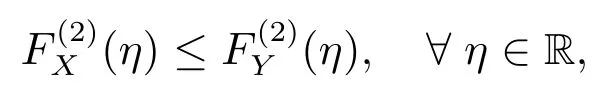
式(2)中Y(D)為基準隨機變量．由SSD 性質(文獻[20]中的2.6,2.7 式)，可知問題(2)等價于

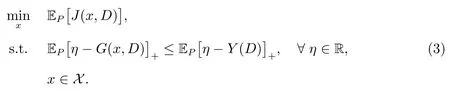
由于問題(3)不滿足Slater 約束規范，所以考慮其松弛問題

稱問題(4)為真問題，這里[a,b]是R 中一個有界閉區間．

3 SAA方法及其收斂性分析

本節研究真問題(4)的SAA 問題．設隨機變量D 的獨立同分布樣本為為方便起見，令Yi=Y(di)，則其SAA 問題為

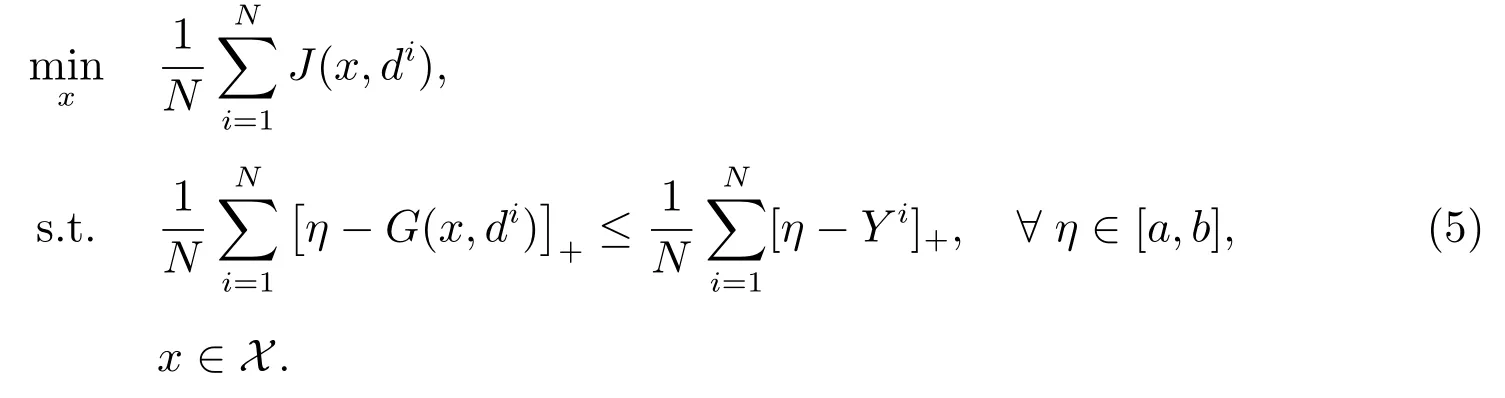
接下來給出SAA 問題(5)的收斂性分析．

3.1 幾乎處處收斂

帶有SSD 約束的優化問題的最優性條件已被Dentcheva 和Ruszczyski[20,21,33]證明．關于該問題的SAA 問題的收斂性在文獻[23,26,34]中也給了出來．這里根據報童問題的特點，利用前述文獻的結果，證明了帶有SSD 約束的多產品報童問題的SAA 問題的收斂性．

為簡化符號，令p(a)=max(0,a)，則有

命題1假設存在點x0∈X, η0∈[a,b]，使得

那么，我們有：

(i) 對任意的x ∈ X, η ∈ [a,b]，f(x)和h(x,η)是有定義的；J(x,D), G(x,D)關于 x 全局 Lipschitz 連續，Lipschitz 系數為

(ii) f(x)和h(x,η)關于x 是全局Lipschitz 連續的，Lipschitz 系數為k；且h(x,η)關于η 也是全局Lipschitz 連續的．

證明 對于結論(i)，由G(x,D)的顯式表達式可知，對xm, m=1,2,··· ,M，有

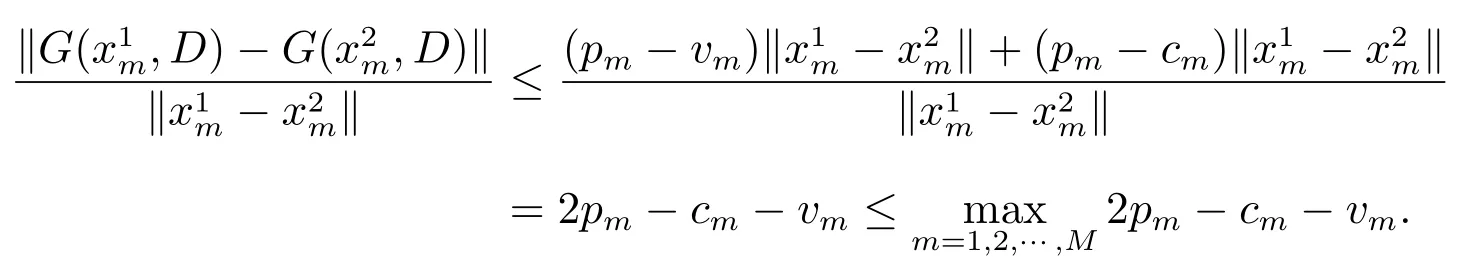
故而J(x,D), G(x,D)關于x 的Lipschitz 系數為

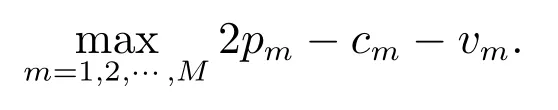
對于結論(ii)，由(i)可知，f(x)和h(x,η)關于x 是全局Lipschitz 連續的，Lipschitz系數為k．又因為H(x,η,D)關于η 是全局Lipschitz 連續的，即

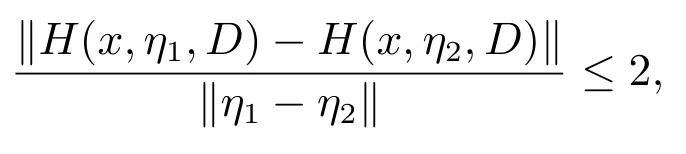
表明h(x,η)關于η 也是全局Lipschitz 連續的．

假設1問題(4)滿足一致占優條件(Slater 約束規范)，即存在x0∈X，使得

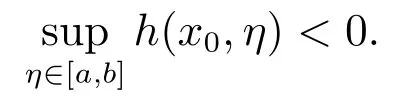
令

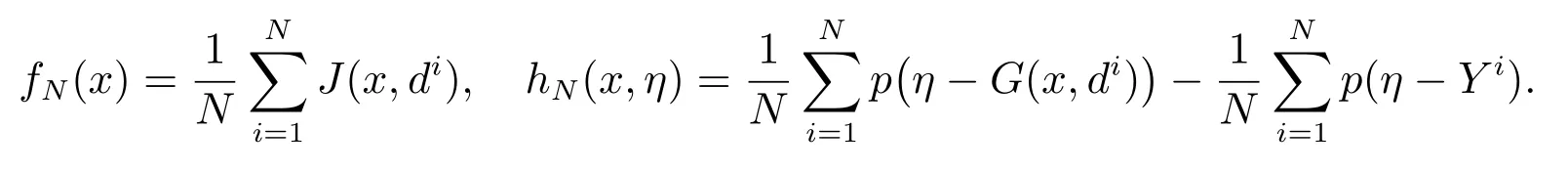
SAA 問題(5)，可以寫成如下形式

設問題(6)的最優值是zN，接下來證明隨樣本量N 的增加，zN收斂于真問題(4)的最優值，將樣本均值逼近寫成特定的概率測度

在隨機規劃中，PN被稱為經驗概率測度．據此將(6)式改寫為

在進行收斂性分析之前定義以下幾個符號：設P(?)表示所有Borel 概率測度的集合；定義函數集

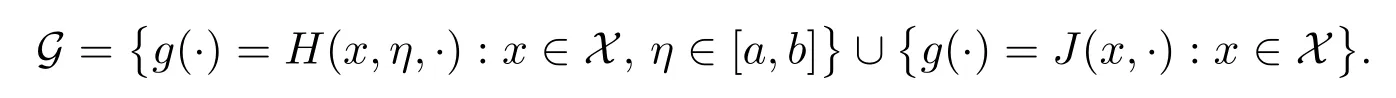
定義PN到P 的偽距離

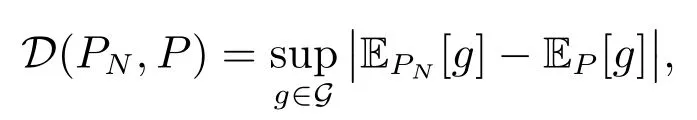
由于H(x,η,·)和J(x,·)是連續的，且X 和[a,b]是緊集，所以PN, P ∈ PG(?)且D(PN,P)<∞．

定理1設：

(i) 假設1 成立；

(ii) 命題1 的條件成立及X 是緊集，則：

1) 對于問題(6)的最優值函數V(PN)，當N →∞時，w.p.1 滿足

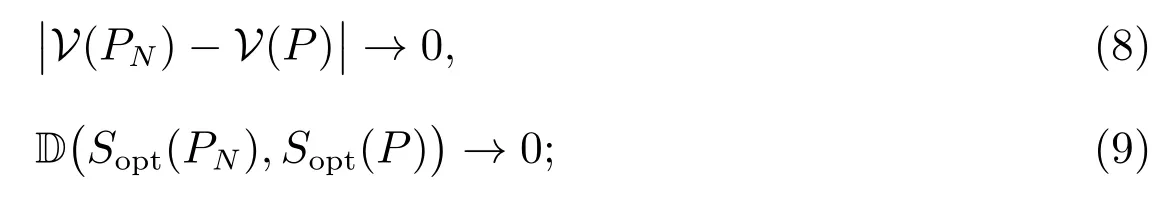
2) 若另有：

(iii) 對任意的x ∈X，當t 趨向于0 時，廣義矩函數

有界，則對任意小的正數γ，存在正整數N?和獨立于N 的正實數C(γ), β(γ)，使得當N ≥N?時，滿足

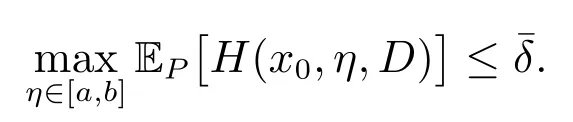
繼而由文獻[23]定理3.1 的結論(i)和文獻[34]定理2.7 的結論(iii)可知，存在正整數L?>0，使得w.p.1

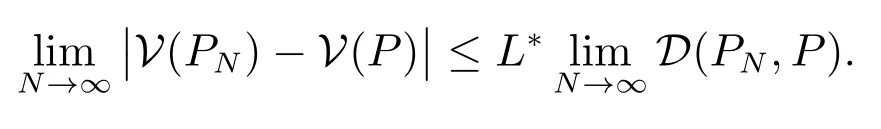
又由命題1 和文獻[23]命題3.1 可知，當N →∞時，有D(PN,P)→0，所以有

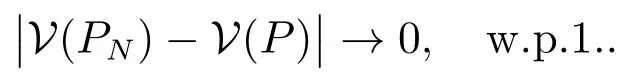
對于(9)式，在命題1 及假設1 的條件下，由文獻[34]定理2.7 的結論(ii)可知Sopt(·)在P 處上半連續．結合文獻[23]命題3.1 可知

對于(10)式，在條件(iii)下，由命題1 和文獻[23]命題3.2 可知，對任意小的正數γ ≤ L???，存在正整數N?和獨立于N 的正實數C(γ), β(γ)，當N ≥ N?時

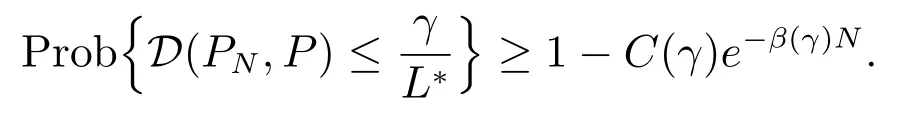
結合文獻[34]定理2.7 的結論(iii)，有

4 數值實驗

由于問題(5)是半無限問題，難以求解，所以考慮在特定條件下將其轉化為有限問題，即考慮其以下等價形式．

假設2隨機變量Y(D)的支持集Y ?[a,b]．

在假設2 下，由文獻[20]的命題3.2 可知問題(5)等價于

稱問題(5)與問題(11)均為SAA 問題．由于問題(5)與(11)的等價性，所以在以下部分以(11)為研究對象．

4.1 切平面算法

Sun 等[26]改進的切平面法適用于解決多個非線性復雜約束的隨機優化問題，這里采用該方法求解問題(11)．

算法1

第1 步令迭代次數t=0，誤差?=10?5，令S0={x|0 ≤ cTx ≤ α}；

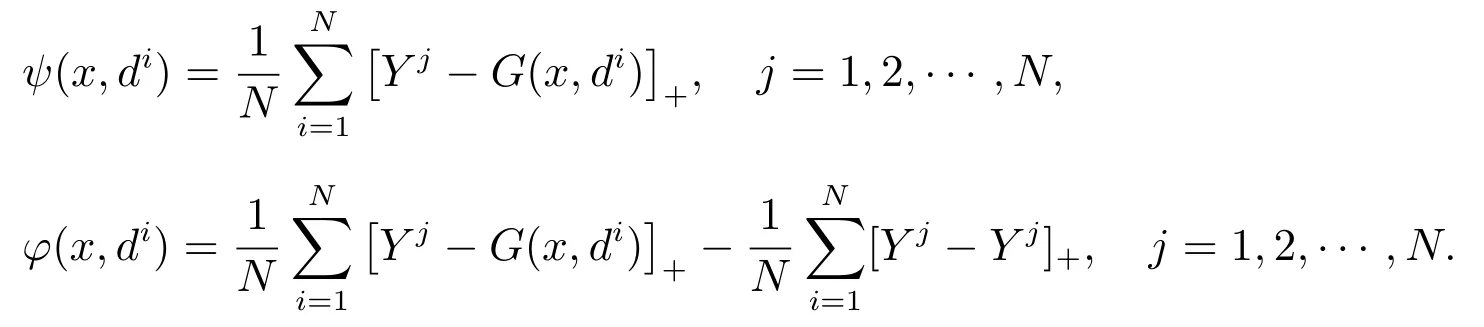
第2 步解決線性規劃問題

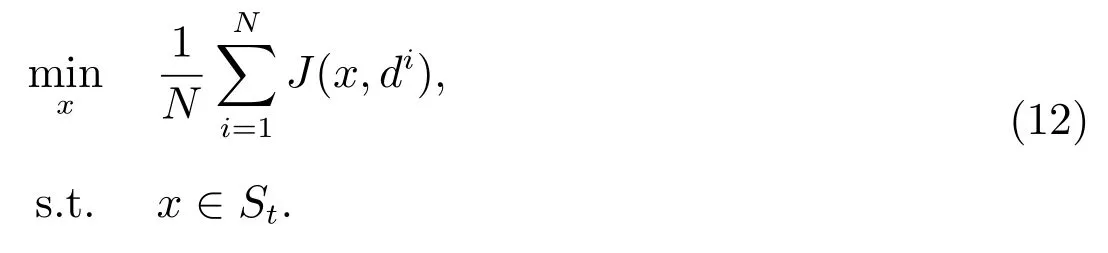
若問題(12)無可行解，則原問題無可行解；否則，設問題(12)的最優解為xt．

第3 步找到，使得

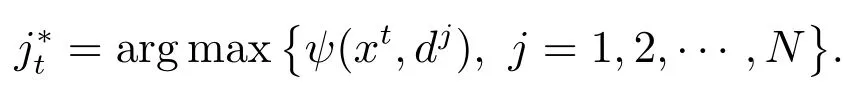
其實質是找到眾多約束中違反度最大的約束．構造索引集

第 4 步若停止，是最優解；否則，構造切平面

轉到第2 步．

4.2 實驗及結果分析

本節考慮零售商需要在銷售季進行五種產品的交易，即零售商需要在期初確定五種產品的訂購量以期獲取最大利潤．假定五種產品的需求服從不同自由度的χ2分布

在此基礎上設置三個示例，例1 采用模型(1)為參照進行樣本內實驗，對SSD 模型的收斂性進行驗證．例2 在模型(1)為參照下，進行樣本外累計預測．例3 以均值-方差(MV)模型為參照模型，進行樣本外累計預測．MV 模型即以最小(大)化隨機損失(利潤)的期望為目標函數，以隨機函數的方差來度量風險．對于報童問題帶有訂購能力約束的MV模型為

其中μ為常數，該模型也是風險厭惡模型．由于參照模型的最優解也屬于緊集X，所以參照隨機變量Y(D)的支持集有界，假設2 成立，從而SAA 問題(5)與(11)等價，這里采用算法1 求解問題(11)．

例1SSD 模型收斂性分析數值實驗

設資金約束α = 3.5，樣本量取10000，求得模型(1)的最優解，作為SSD 模型的參照．然后在SSD 模型的求解中，樣本量依次設為100、1000、2000、3500、5500．每個樣本量下進行30 次實驗，其結果如圖1 所示，圖中每一個垂直區間表示在對應樣本量下30 個最優解的范圍．該圖顯示了SSD 模型下最優解隨樣本量增大而逐漸收斂的特性．

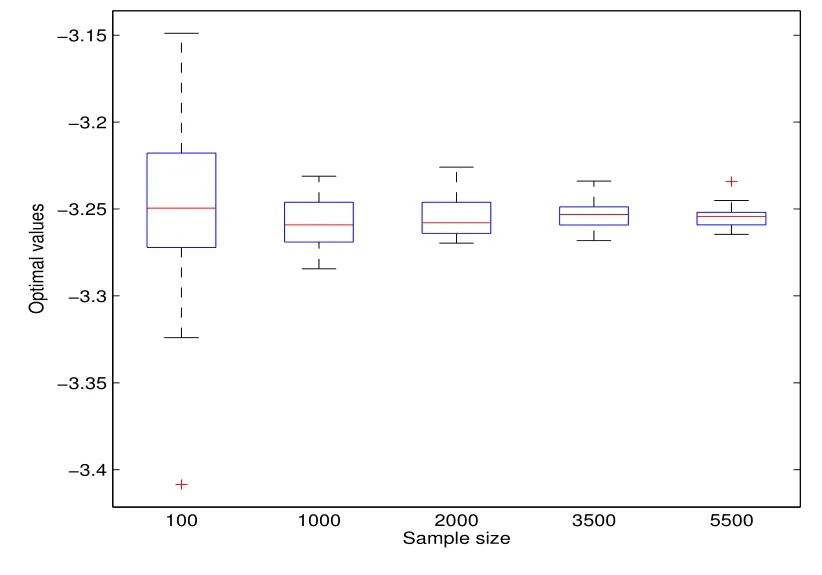
圖1: 例1 隨樣本量增加SAA 問題的收斂性

例2以模型(1)為參照的SSD 模型樣本外累計預測

假設零售商在有限購買能力下訂購商品并出售，而后將利潤累計到資本，直到最優訂購量的金額不受資本約束為止．樣本量N 取3000，初始資本設為0.7，在此條件下，本例在每輪訂購下均進行10 次抽樣，求得樣本外預測的利潤均值，以該均值作為資本累計，經過5 輪累計之后，累計資本大于最優訂購量下的成本，停止累計．

本例資本累計的步驟如下：

步驟1在相同初始資本下，模型(1)與SSD 模型各自以其最優訂購策略實現其預期利潤；

步驟2模型(1)以其自身利潤為累計資本，求得最優解；

步驟3模型(1)以SSD 模型利潤為累計資本，求得最優利潤作為基準；在該基準下，SSD 模型以其自身利潤為累計資本，求得最優解；

步驟4返回步驟2．

表1 和圖2 均說明，在同樣的樣本下，平均利潤SSD 模型優于模型(1)．圖3 顯示了第四次樣本外累計預測10 次抽樣的結果，此時在訂購能力約束下，SSD 模型下的利潤高于模型(1)，這就使得在SSD 模型下，零售商可實現以更快的速度達到累計資本的目的，以擺脫訂購能力約束．圖4 顯示了第五次樣本外累計預測10 次抽樣的結果，表明當累計資本充足，即零售商不再受訂購能力約束時，SSD 模型能夠以更少的投資獲得更大的利潤．

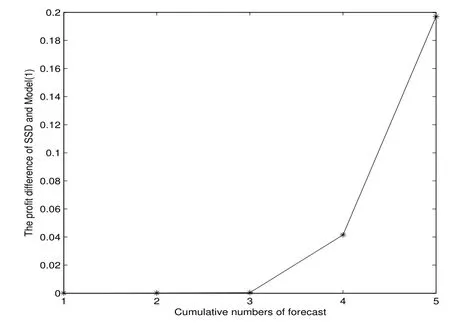
圖2: 例2 樣本外累計預測平均利潤差

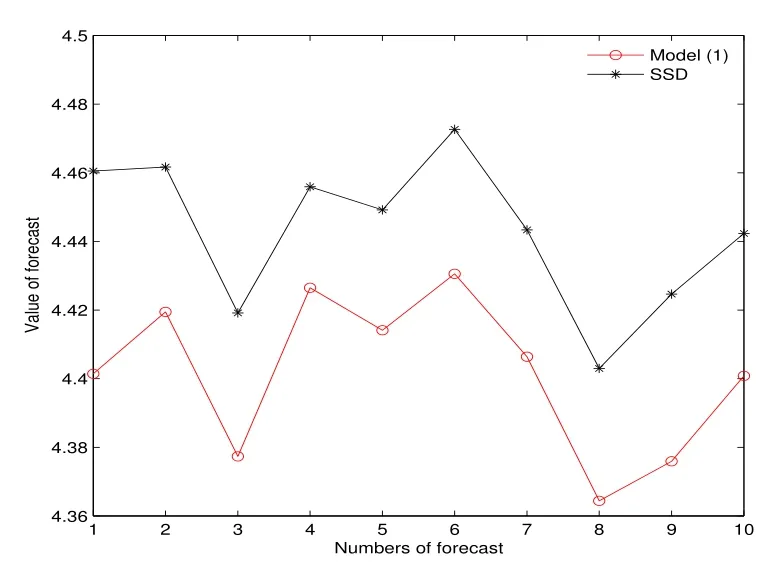
圖3: 例2 第四次預測

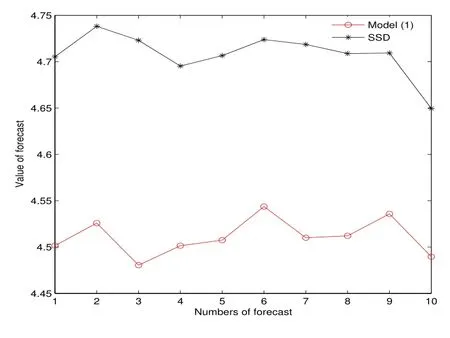
圖4: 例2 第五次預測

例3以MV 模型為參照的SSD 模型樣本外累計預測

采用例2 的資本累計步驟，以MV 模型為參照，設μ=0.3，所得結果如表2、圖5 至圖7 所示．

表2、圖5 至圖7 表明，樣本外累計預測下，SSD 模型的利潤優于MV 模型，且這種占優趨勢隨著資本累計越來越明顯．其中圖6 和圖7 分別為第四次、第五次樣本外10 次抽樣的利潤．

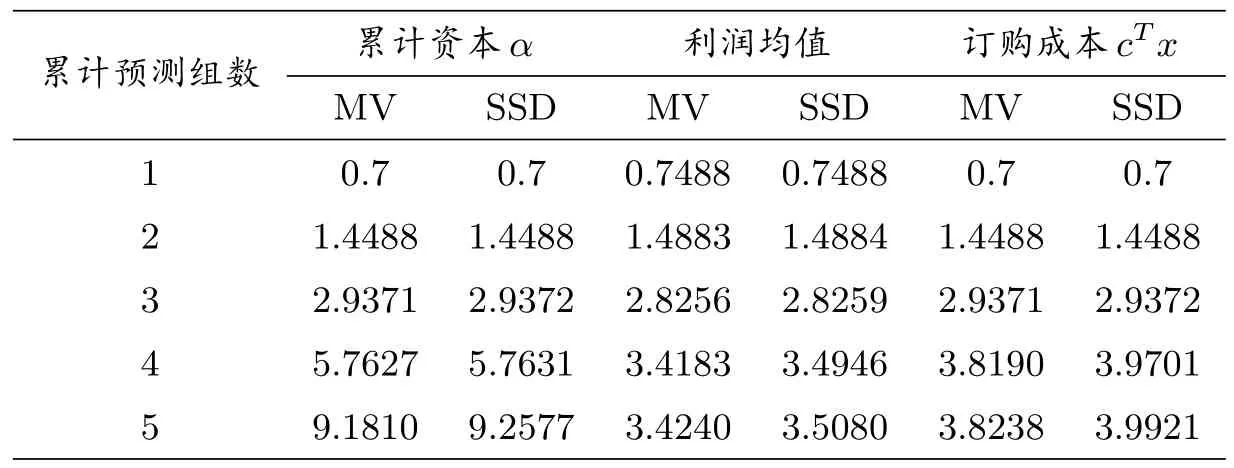
表2: 例3 樣本外累計預測

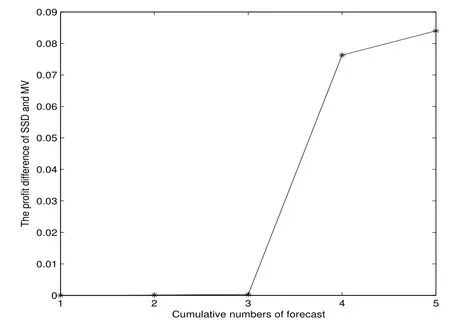
圖5: 例3 樣本外累計預測平均利潤差

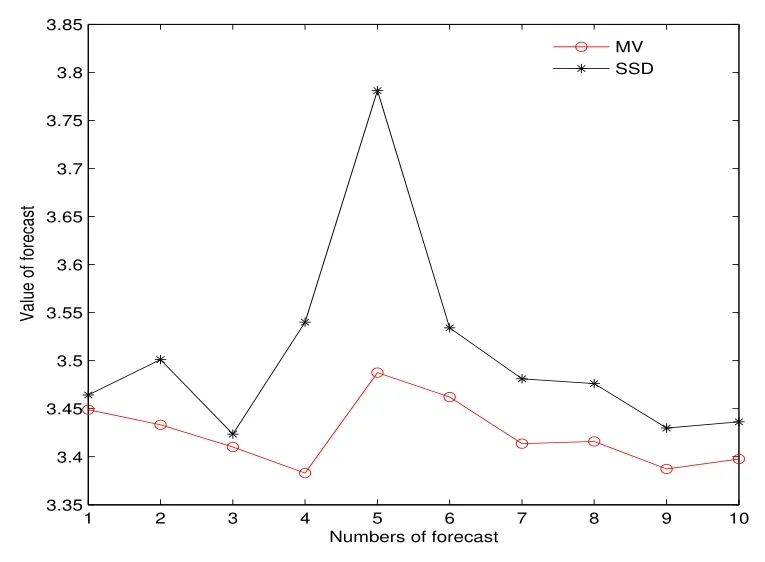
圖6: 例3 第四次預測

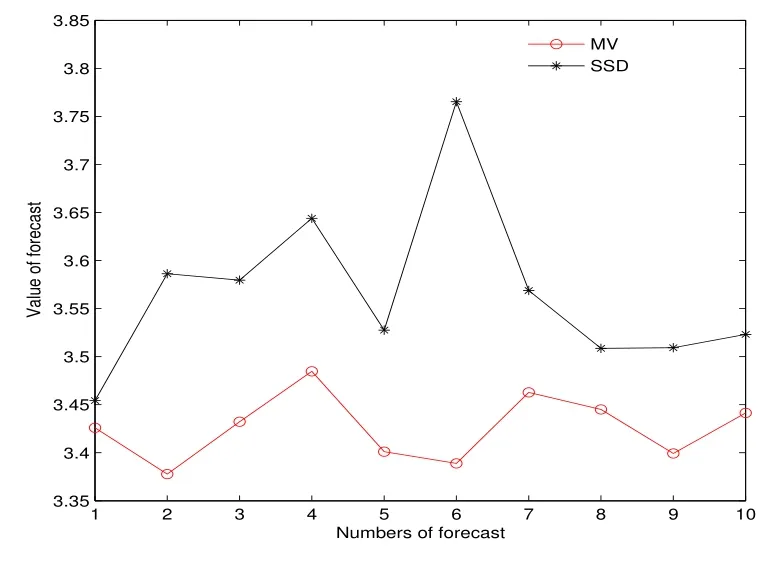
圖7: 例3 第五次預測

5 總結

本文以單周期多產品報童問題為背景，在訂購能力約束及SSD 約束下進行建模．對SAA 問題進行收斂性分析并通過切平面法對SAA 問題進行求解．以風險中性模型(模型(1))及風險厭惡模型(MV 模型)為參照下，通過樣本外預測表明了SSD 模型的優越性．SSD 模型具有良好的風險規避性，決策者可以該模型的訂購策略作為自身決策的評價和基準，具有重要的現實意義．基于本文的研究可以繼續探討多產品多周期的情形，以及風險厭惡條件下多級供應鏈的協調等．