廣義神經(jīng)傳播方程的Wilson 元收斂性分析

梁聰剛， 張厚超， 石東洋

（1.平頂山學(xué)院 數(shù)學(xué)與統(tǒng)計學(xué)院，河南 平頂山467000； 2.鄭州大學(xué) 數(shù)學(xué)與統(tǒng)計學(xué)院，河南 鄭州450052）

神經(jīng)傳播過程中，神經(jīng)傳播信號及它關(guān)于時間和空間的變化率，在數(shù)學(xué)上表現(xiàn)為一類非線性擬雙曲方程［1］

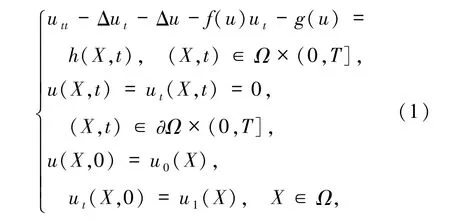
其中，Ω∈R2是矩形區(qū)域，?Ω 為其光滑邊界，X =（x，y），u0（X）及u1（X）是已知光滑函數(shù)，f（u），g（u）及其偏導(dǎo)數(shù)對變量u滿足Lipschitz連續(xù).

非線性擬雙曲方程是近年來發(fā)展起來的一類重要的非線性發(fā)展方程，它在生物、力學(xué)等領(lǐng)域有著廣泛的應(yīng)用［2］.文獻［3］研究了該類方程初邊值問題解的長時間行為.文獻［4］對高維廣義神經(jīng)傳播方程的整體光滑解進行了研究.文獻［5］給出了全離散的Galerkin近似.文獻［6 -7］討論了該類方程的A.D.I.有限元方法和特征差分法.文獻［8 -10］分別利用雙線性元，Hermite 型矩形元和類Wilson元得到了該類方程的超收斂和外推結(jié)果.文獻［11］應(yīng)用Crouzeix -Raviart 非協(xié)調(diào)線性三角形元得到了變網(wǎng)格下的最優(yōu)誤差估計.文獻［12］考慮了該類方程的各向異性非協(xié)調(diào)有限元的超收斂分析.文獻［13 -14］研究了混合有限元格式，得到了半離散格式下的最優(yōu)誤差估計.文獻［15］利用EQrot1元及零階R-T元建立一個低階非協(xié)調(diào)混合元格式，得到了超逼近結(jié)果.然而，我們發(fā)現(xiàn)上述文獻提高收斂階的方法大多是利用插值后處理技術(shù)，外推或者構(gòu)造新的單元.文獻［16 -17］在研究二階拋物和橢圓問題時，借鑒了文獻［18 -19］的思想方法，利用內(nèi)部懲罰方法構(gòu)造了一個新的離散變分形式，并在雙線性型中添加了穩(wěn)定項，使得Wilson元相容誤差項變成了0，收斂階提高到O（h2）.

本文的主要目的是將文獻［16 -17］的思想應(yīng)用于問題（1）的收斂性研究.首先，證明了半離散格式逼近解的存在唯一性.其次，利用Wilson 元在新范數(shù)意義下的插值估計和雙線性型的性質(zhì)導(dǎo)出了半離散格式下原始變量u 在新范數(shù)意義下O（h2）階的收斂結(jié)果.最后，通過構(gòu)造一個二階的全離散格式，得到了相應(yīng)的O（h2+τ2）階高精度結(jié)果，這是文獻［16 -17］未涉及的.

本文中，Ws，p（D）（D?Ω）表示通常的Sobolev空間，‖·‖s，p，D和｜·｜s，p，D分別表示其上的范數(shù)和半范，其中s為非負(fù)整數(shù)，1≤p≤∞.當(dāng)p =2 時，記Ws，2（D）= Hs（D），‖·‖s，D和｜·｜s，D分別表示Hs（Ω）上的范數(shù)和半范，當(dāng)D =Ω時，省略下標(biāo)D.約定

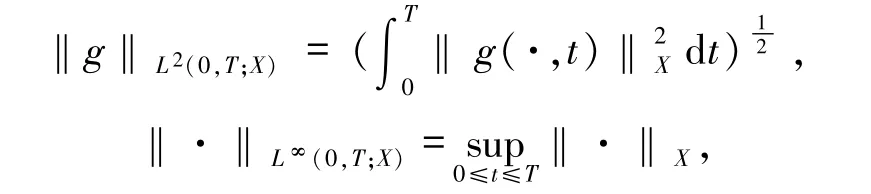
其中X為Banach空間.本文中，C 是與h 和τ 無關(guān)的正常數(shù)，在不同的地方取值可以不同.

1 單元的構(gòu)造及性質(zhì)

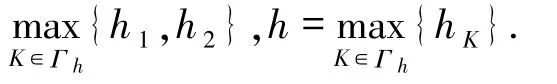
設(shè)εh表示所有單元邊界所成的集合，E表示單元邊界，hE表示E的長度.規(guī)定函數(shù)f 在相鄰單元K和K′的相交邊上的跳躍值和平均值分別為

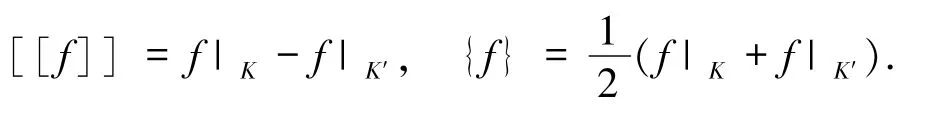
Wilson元的形函數(shù)空間為P2（K），有限元空間為定義在Ω上，vh｜K∈P2（K），vh在內(nèi)節(jié)點處連續(xù)，在邊界?Ω上節(jié)點處為0｝，其中vh｜K由4 頂點函數(shù)值以及和確定.

定義Vh上的模和雙線性型［16］分別為

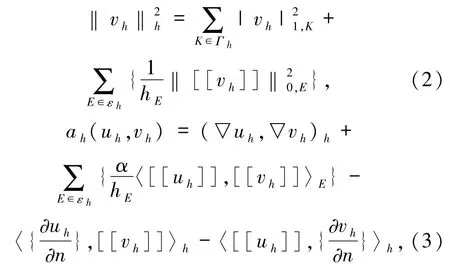
其中

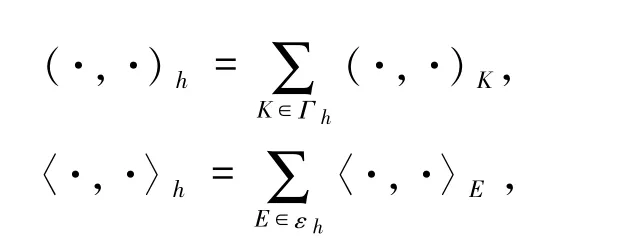
α是待定常數(shù).顯然有‖vh‖0≤C‖vh‖h成立.Ih：H2（Ω）→Vh為相應(yīng)的插值算子.

文獻［16 -17］已證明如下3 個結(jié)論.

引理1.1設(shè)u∈H3（Ω），則有

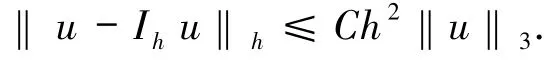
引理1.2設(shè)｛Γh｝是區(qū)域Ω的正則矩形剖分，即存在σ ＞0，使得?K∈Γh，有.則存在0，使得

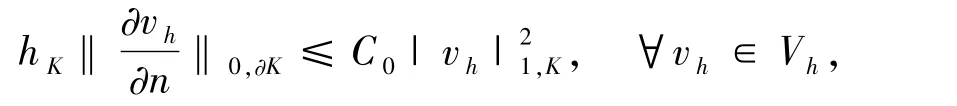
引理1.3是連續(xù)的，V-橢圓的雙線性型，則，使得

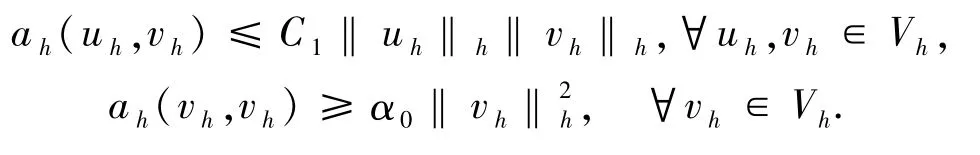
2 半離散格式的收斂性分析

與（1）式等價的變分問題為：求u∈H10（Ω），使得

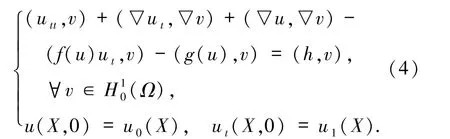
（4）式的傳統(tǒng)半離散格式為：求uh∈Vh，使得

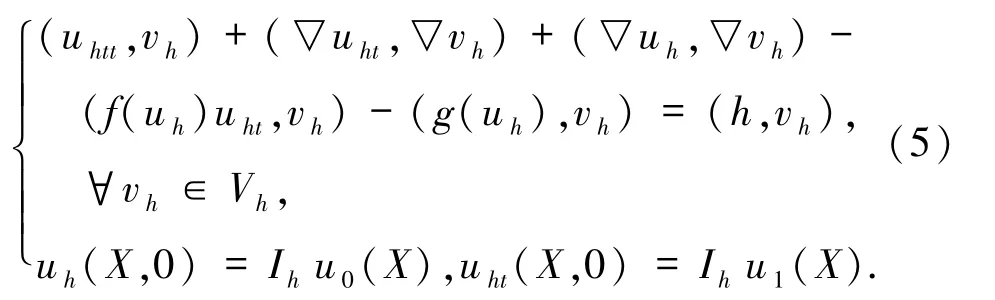
為提高逼近精度，我們引進新的半離散格式為：求uh∈Vh，使得

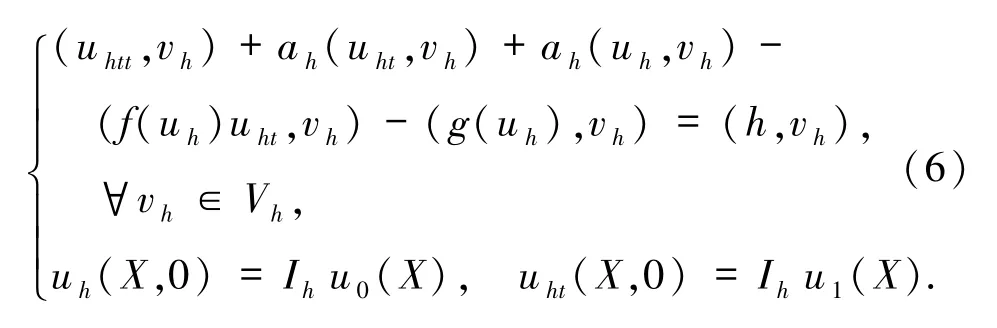
定理2.1問題（6）存在唯一解.

證明設(shè)是Vh的基函數(shù)，則

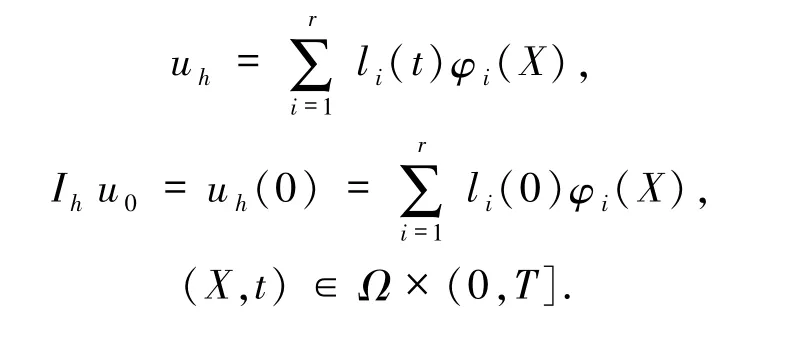
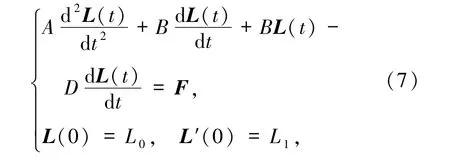
其中L0，L1是已知的，由

決定，

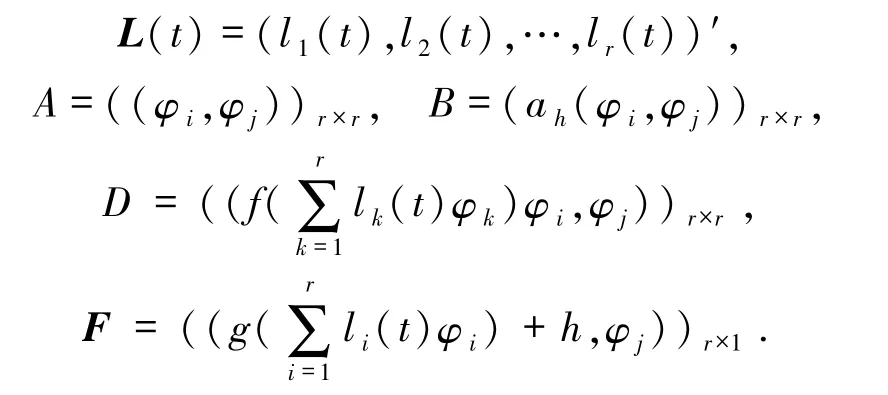
從而（7）式是關(guān)于向量函數(shù)L（t）的一個常微分方程組.根據(jù)常微分方程的理論，注意到A 是正定對稱矩陣，對于給定初值L（0），L′（0），它的解是唯一存在的.因而問題（6）的解存在唯一.證畢.

下面先討論上述問題的收斂性.

定理2.2設(shè)u、uh分別是（1）和（6）式的解.設(shè)u，ut∈H3（Ω），utt∈H2（Ω），則有

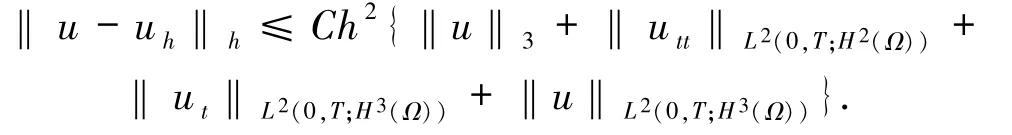
證明令由于u∈H3（Ω），則有

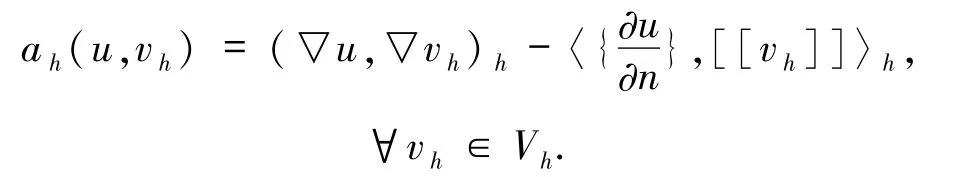
根據(jù)（1）和（6）式有下面誤差方程

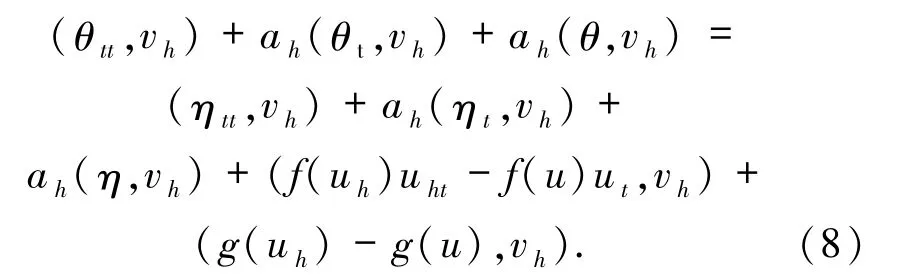
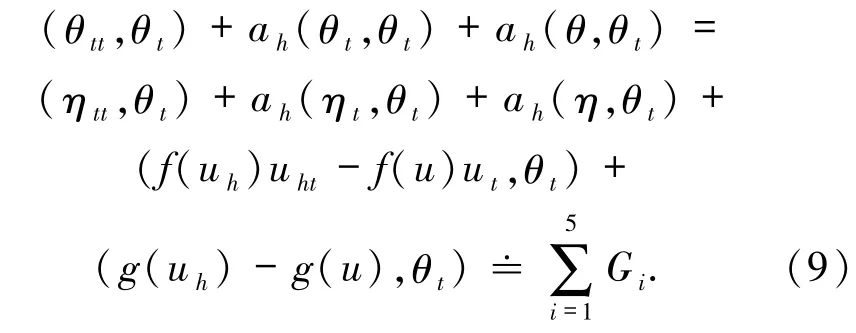
首先注意到

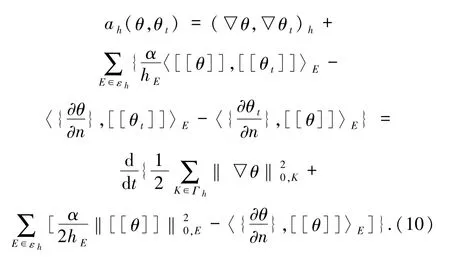
下面對Gi（i=1，2，…，5）進行估計.

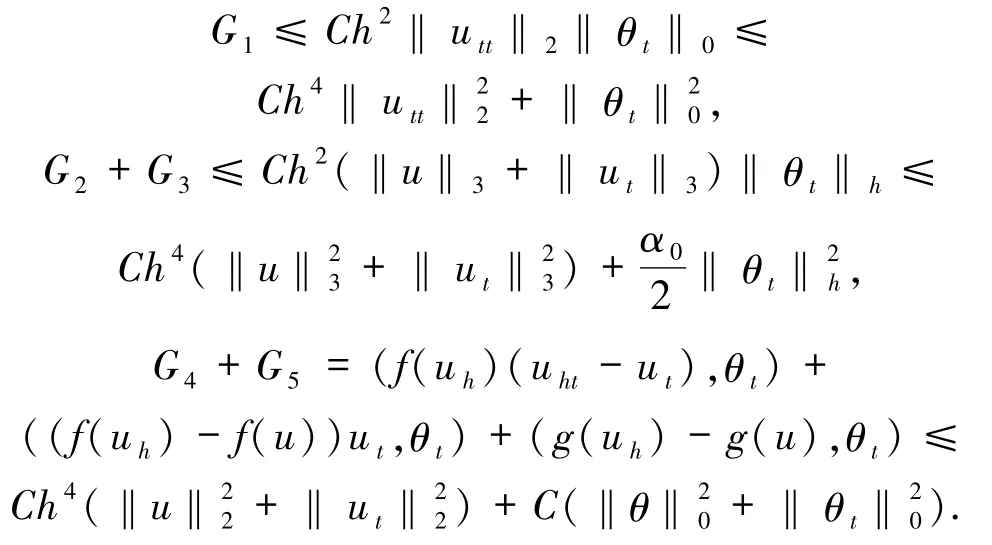
將Gi（i =1，2，…，5）的估計及（10）式代入（9）式，則有

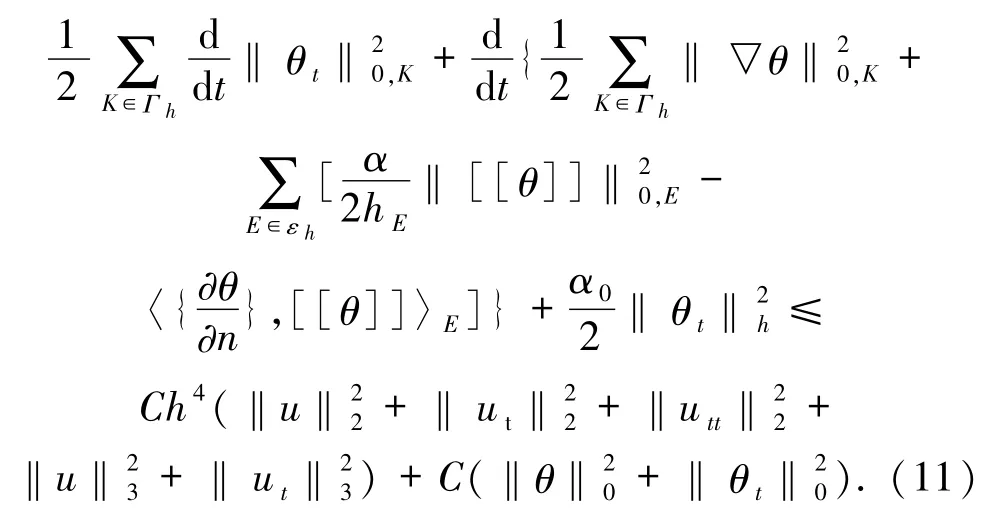
對（11）式兩邊對變量t 從0 到t 求定積分，注意到θ（X，0）=0，θt（X，0）=0，則有

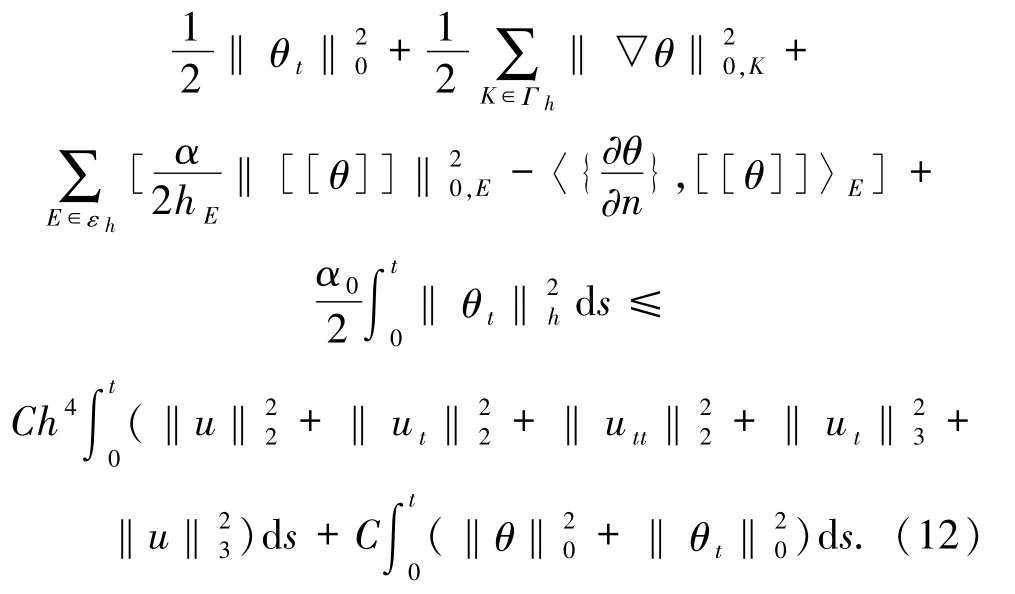
由文獻［16］知（12）式左端可化為

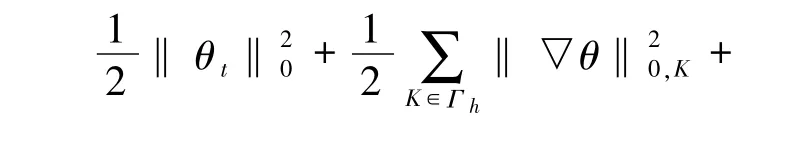
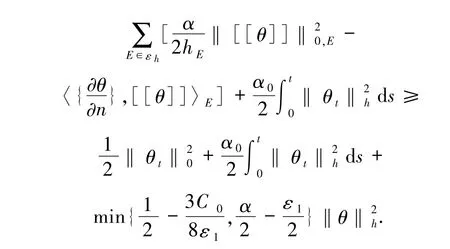
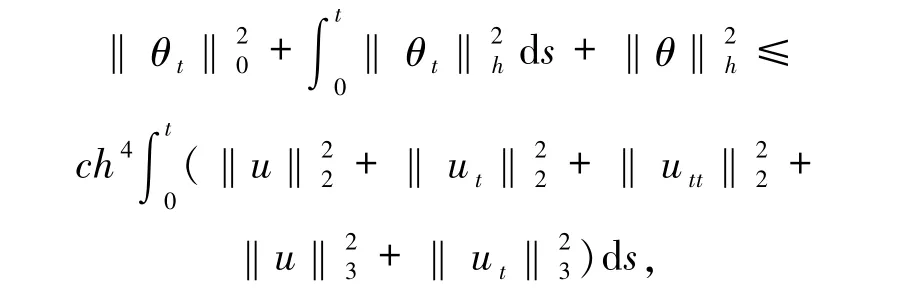
即

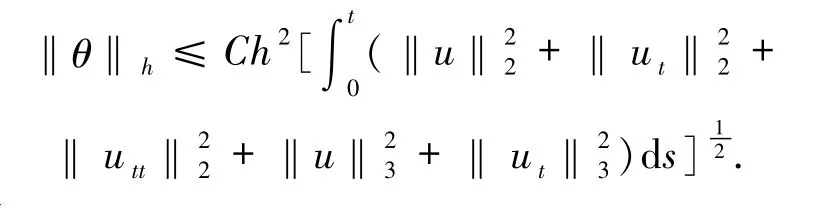
因此

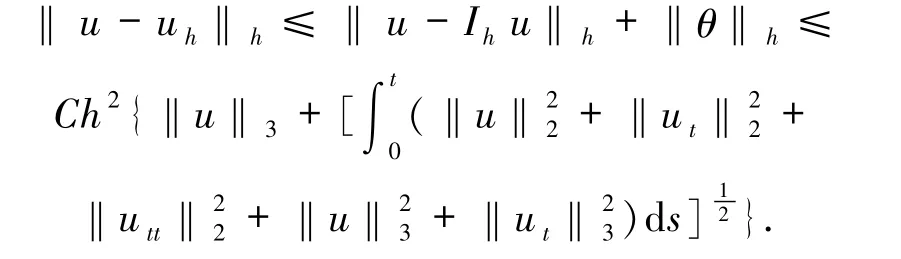
證畢.

3 全離散逼近格式的收斂性分析

在本節(jié)中，將給出問題（4）的全離散逼近格式及相應(yīng)的誤差估計.將時間區(qū)間［0，T］進行N 等分，即，則時間步長τ =在Vh中的逼近，對于［0，T］上的任意光滑函數(shù)ψ，定義

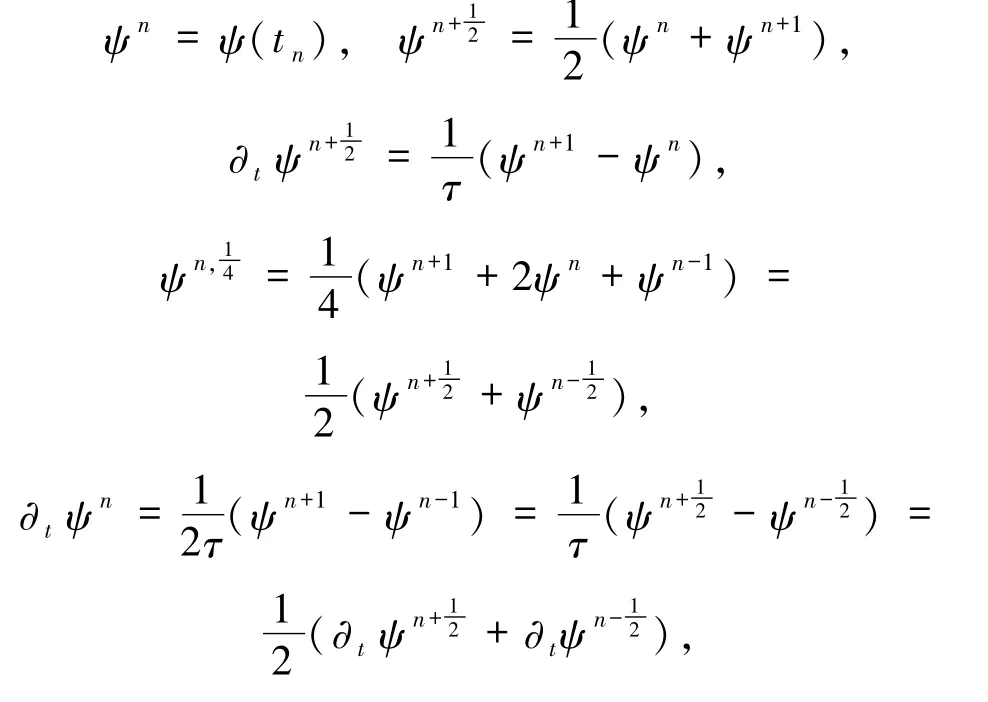
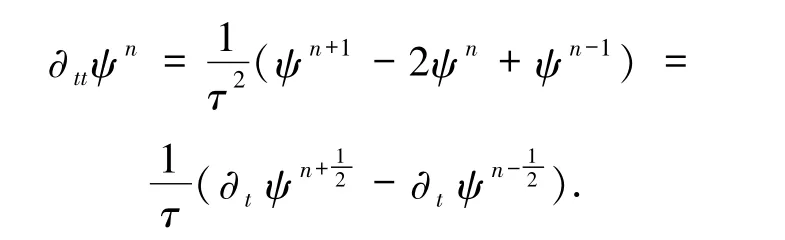
建立（4）式的全離散逼近格式如下：求Un∈Vh，使得

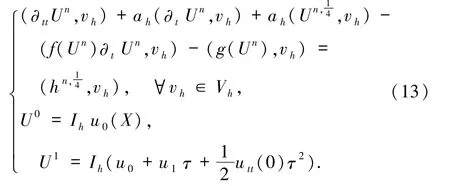
定理3.1設(shè)un、Un分別是（1）和（13）式的解，若

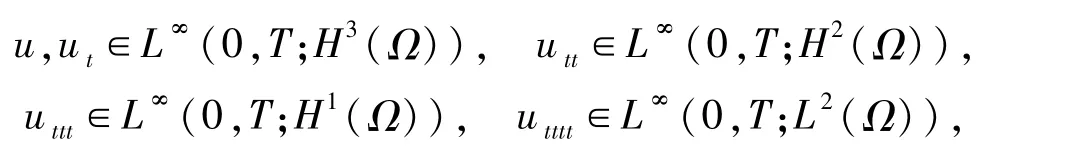
則有

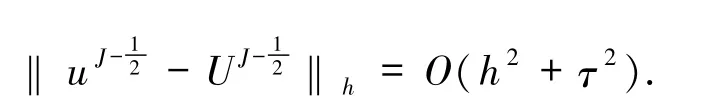
證明令

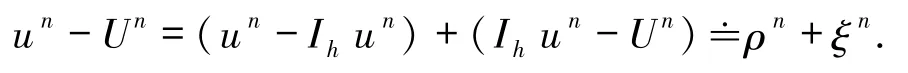
由（1）和（13）式得誤差方程為

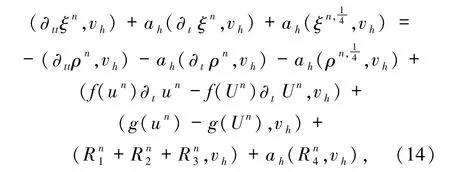
其中，

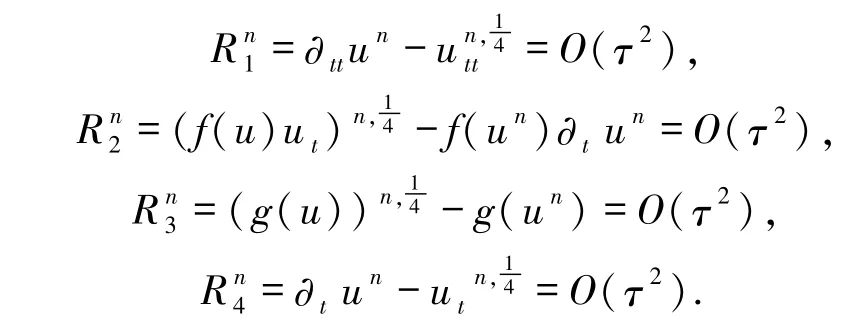
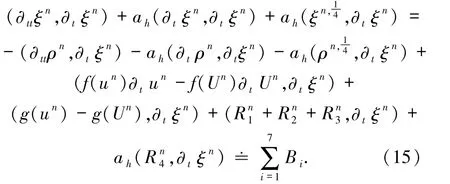
首先注意到

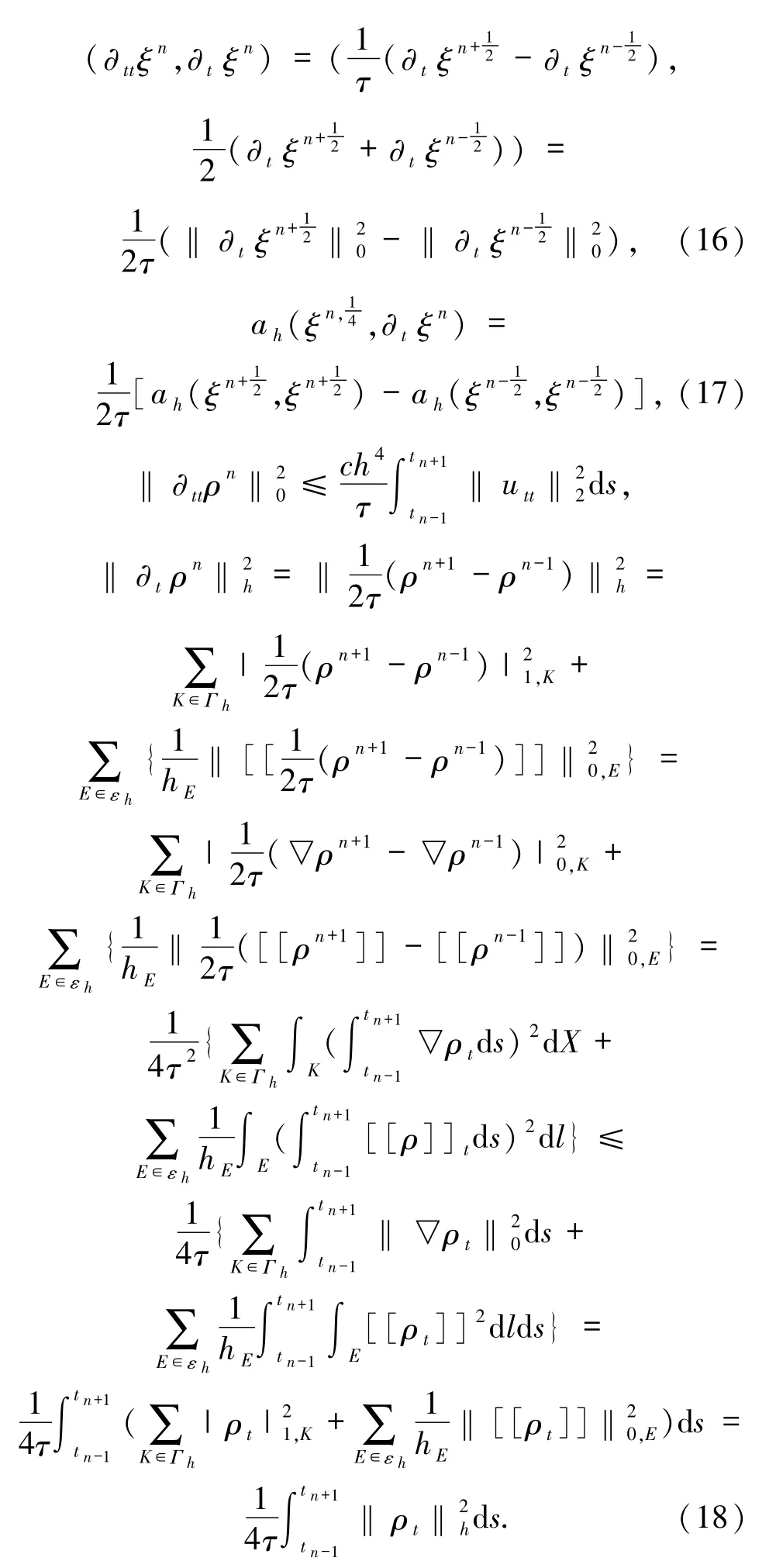
下面對Bi（i=1，2，…，7）進行估計.

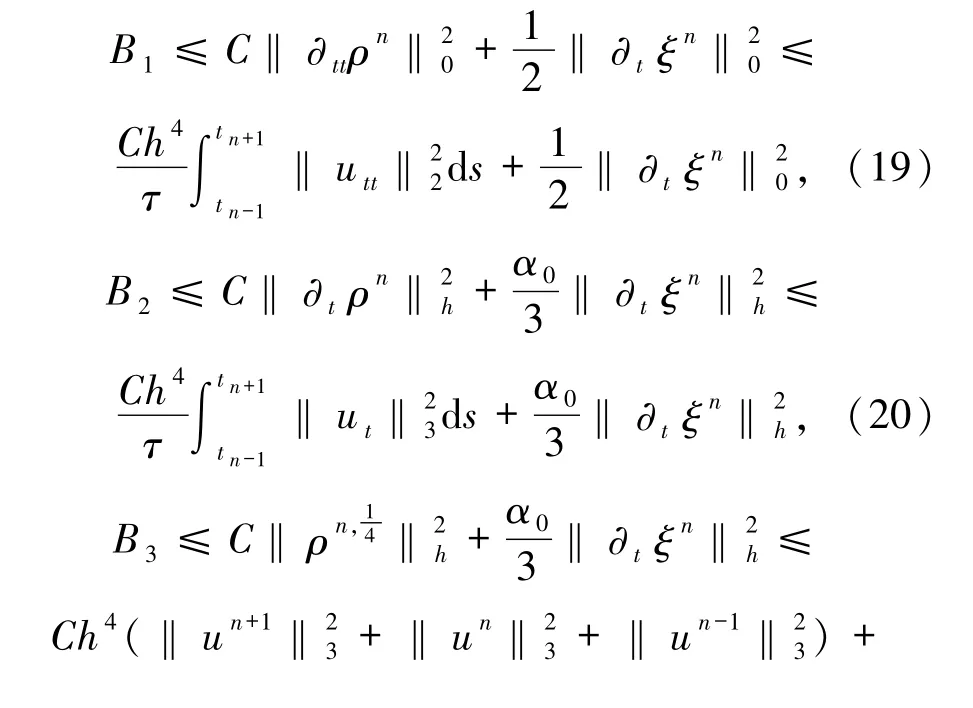
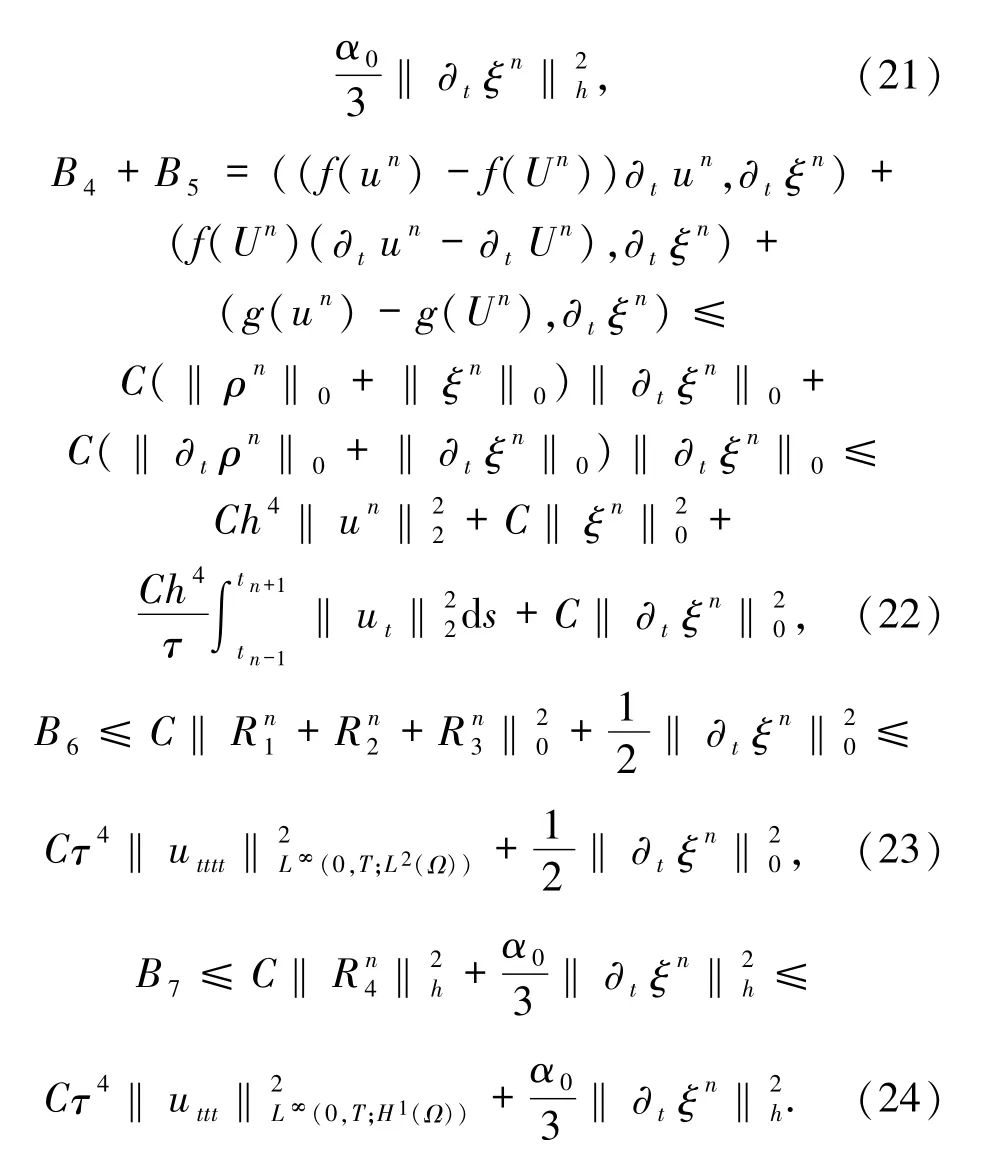
將（16）～（24）式代入（15）式，兩邊同乘2τ，再關(guān)于n從1 到J-1（J≤N）求和，得

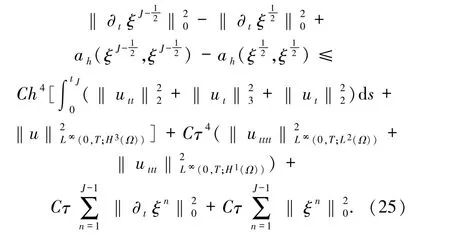
再利用

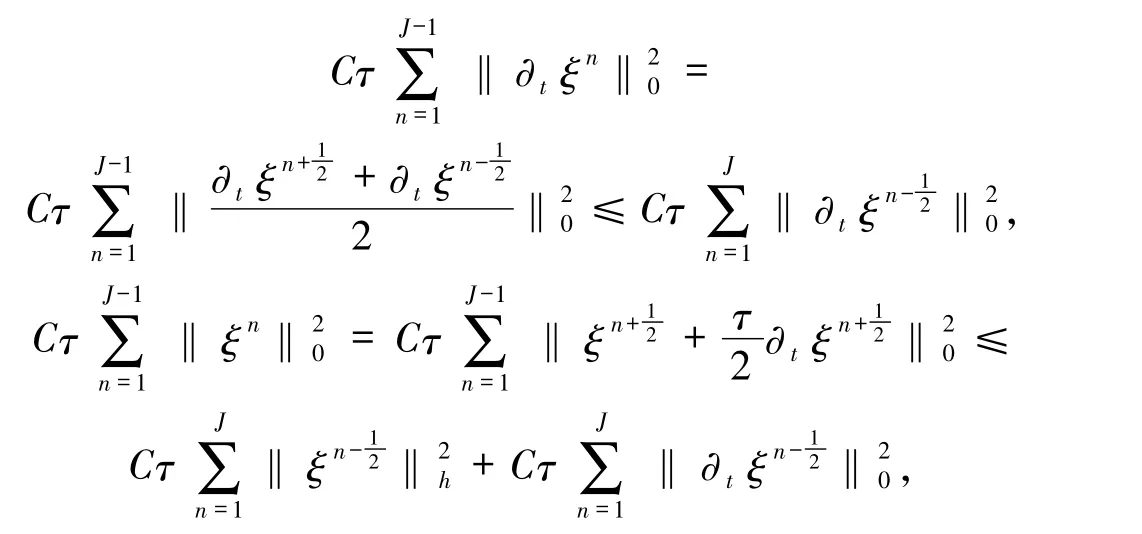
則有

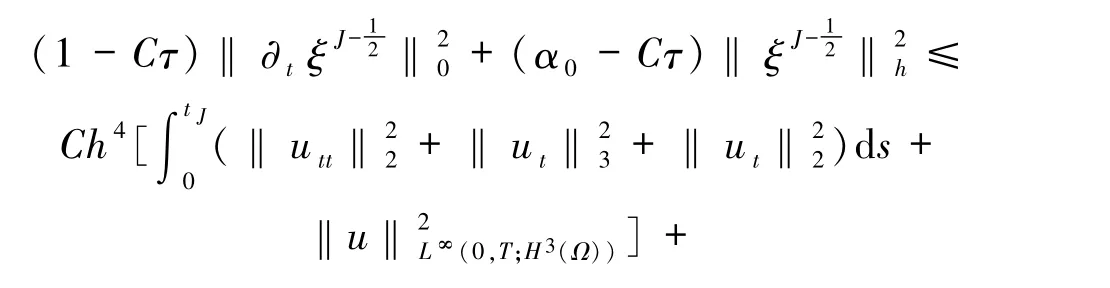
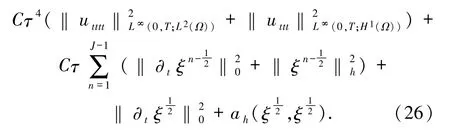
下面來估計上式右端后兩項.利用泰勒公式有

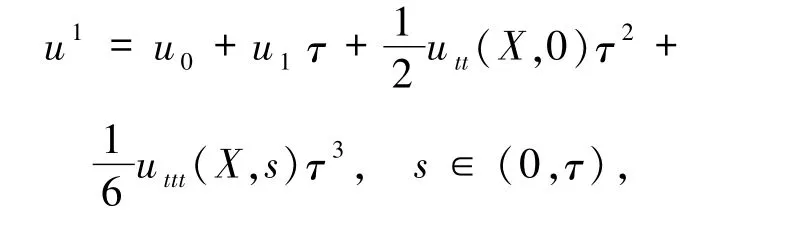
從而

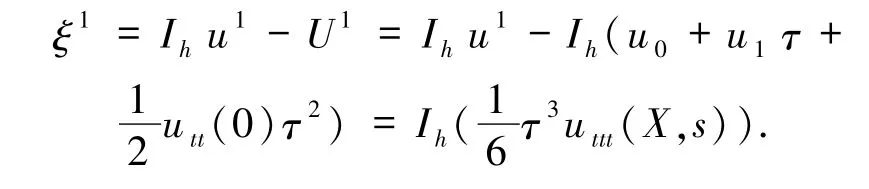
所以

將（27）和（28）式代入（26）式，當(dāng)1 -Cτ ＞0 且Cτ ＞0 時，利用離散的Gronwall引理有

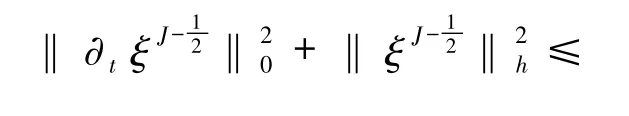
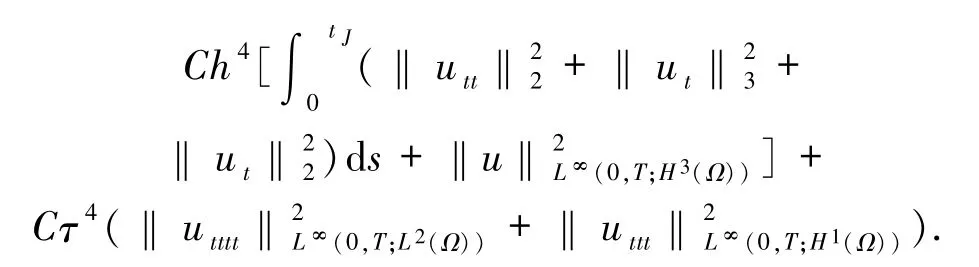
因此

證畢.

4 結(jié)論

本文通過引入新的雙線性型，對廣義神經(jīng)傳播方程分別構(gòu)造了一種新的半離散格式和全離散格式，并且在比傳統(tǒng)的能量模更大的范數(shù)意義下，得到了相應(yīng)的比通常估計方法高一階精度的收斂結(jié)果.在整個分析過程中，對（18）式的估計起到了關(guān)鍵作用.本文對其他偏微分方程的數(shù)值求解提供了可借鑒的思路和途徑.