一種信息不完備條件下的艇員棄艇脫險決策模型研究

(海軍潛艇學院，山東 青島 266071)

0 引言

從理論上說，當潛艇發生海難事故后，艇員在艙室等待援救是比較安全的方法。但是，實際情況往往是等不到外部援救抵達，艙室情況即快速惡化而不得不棄艇脫險。如果指揮員過早下達棄艇脫險命令，可能會失去成功控制海難的機會，使軍隊財產蒙受巨大損失；反之，如果過晚下達棄艇脫險命令或錯誤選擇在艙室等待救援，艇員可能喪失離艇可能性，生命安全得不到保障。因此，為了最大程度保證潛艇艇員成功脫險，指揮員需要根據實際情況準確、快速地作出棄艇脫險的決策。

理想情況下，指揮員可以獲得多方面的失事信息(如海洋環境要素、艙室環境要素、裝備狀態要素、人員狀態要素等)，并依據這些信息和相應的計算分析模型進行棄艇脫險與待援決策。但是，在失事狀態下，往往得不到需要的足夠信息或信息不明朗，這時，指揮員往往根據直覺和個人經驗來處理，難免考慮不周、思維出現混亂而作出錯誤決策，盡管廣大指戰員和科研人員對于棄艇脫險決策的重要性早有認識，由于決策的目標環境和決策者十分特殊，對于該問題的研究還相當缺乏。

層次分析法(Analytic Hierarchy Process，AHP)是美國運籌學家T．L．Saty教授于20世紀70年代初期提出的一種簡便、靈活而又實用的多準則決策方法，它是一種定性和定量相結合的、系統化、層次化的分析方法，它把一個復雜問題分解成若干組成因素，并按支配關系形成層次結構，然后應用兩兩比較的方法確定決策方案的相對重要性。該方法尤其適合于對決策結果難于直接準確計量的場合。本文針對棄艇脫險這種信息量化不確定、多因素、多目標的現場決策問題，采用層次分析理論進行了輔助建模和探索。

1 模型探討

在失事潛艇的棄艇脫險問題的決策分析中，指揮員會面臨海損程度、外界環境、艙室大氣環境、艙內備品、人員心理狀態、訓練素質、設備狀態等諸多因素，這些因素層面不同、互相關聯、相互制約，共同對指揮員產生心理影響。下面，針對這樣一個紛繁復雜、缺少定量數據的系統，以棄艇脫險決策為目標進行決策建模探討。依照層次分析法理論，建模過程大體上可按下面4個步驟進行。

1.1 遞階層次結構的建立

應用AHP分析決策問題時，首先要把問題條理化、層次化，構造出一個有層次的結構模型，在這個模型下，復雜問題被分解為元素的組成部分，這些元素又按其屬性及關系形成若干層次，上一層次的元素作為準則對下一層次有關元素起支配作用。通過對失事潛艇的脫險決策目標的系統分析，潛艇失事狀態下指揮員需要在3項決策策略(立即棄艇C1、擇機棄艇C2、艙室待援C3)間作出最佳選擇。而影響目標決策的因素主要有8個方面，本著快速、簡潔、實用的原則，本文建立如圖1所示的3層次結構模型，目標層A是需要決策的問題，即本文探討解決的問題，對該問題的解決有賴于對準則層B中8個方面因素的綜合考慮，而方案層C則是解決目標A的可用候選方法，顯然，不同的失事事故中，準則層B的各個因素對方案層C中有不同的影響程度。

1.2 構造判斷矩陣

在建立層次結構以后，上下層元素間的隸屬關系就被確定了。假定上層元素為V，所支配的下一層次的元素為u1，u2，…，un，接下來需要確定下層次各元素對于V的相對重要性(權重)。由于對于本文探討的問題，下層次各元素u1，u2，…，un對于V的重要性無法直接定量表示，需要尋找適當的方法導出它們的權重，為此，本文依據圖1建立的遞階層次結構，采用Saty等人用實驗方法制定的準則去反復比較2個候選方法相對上層目標的相對重要性。由此，得到準則層兩兩比較矩陣(見表1)和8個方案層兩兩比較矩陣(見表2)。

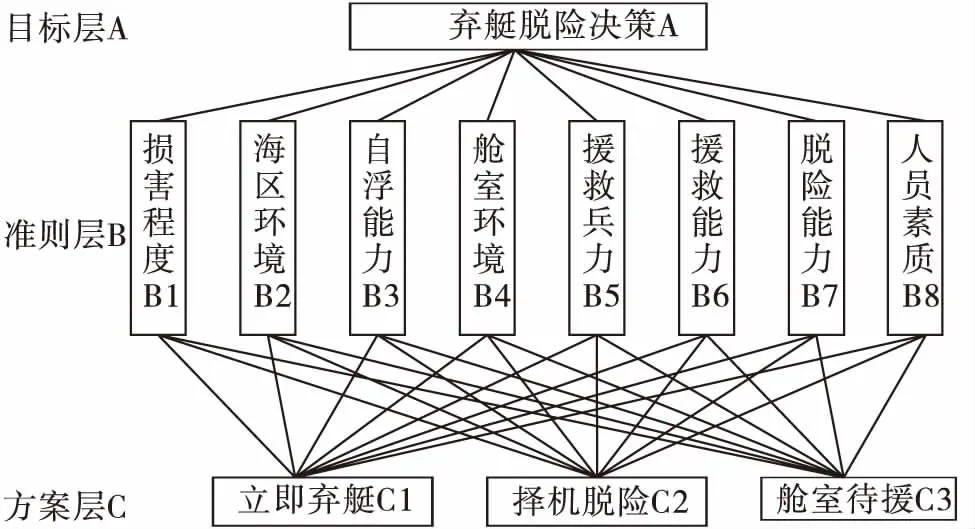
圖1 問題的層次結構示意圖

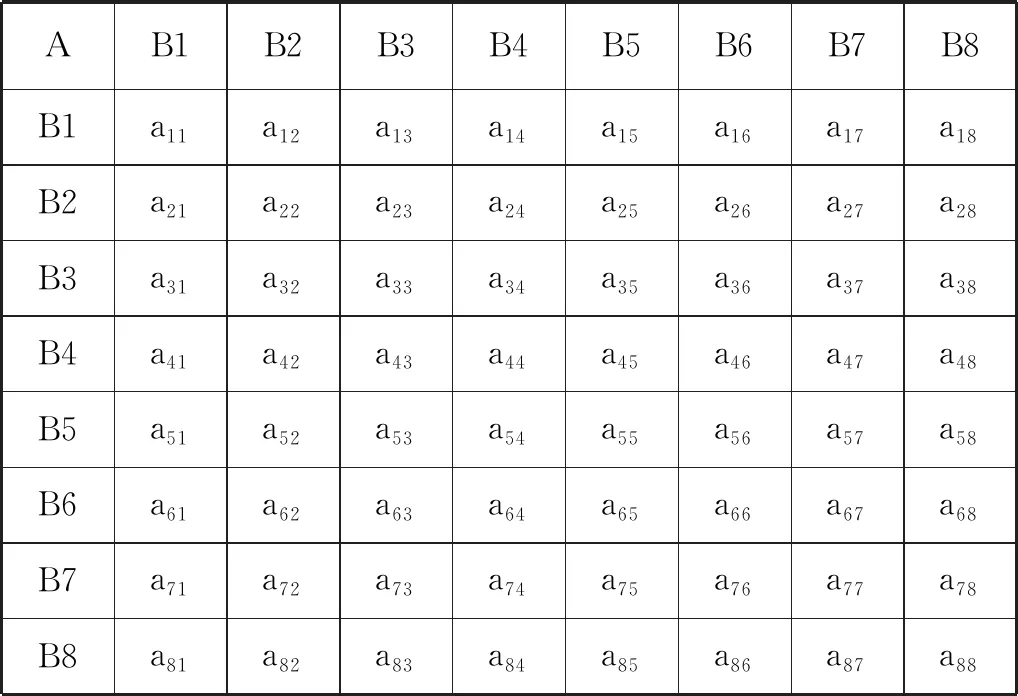
表1 準則層矩陣

式中：aij——縱列因子Bi與橫列因子Bj相比較的結果，見表2。

表2方案層矩陣

兩兩比較時使用的比較準則如表3所示。

表3 比較準則

1.3 層次單排序及一致性檢驗

獲得了判斷矩陣后，計算矩陣對應于最大特征值λmax的特征向量W，經歸一化后即為同一層次相應因素對于上一層次某因素相對重要性的排序權值，這一過程稱為層次單排序。通過兩兩成對比較得到的判斷矩陣不一定滿足矩陣的一致性條件，需要對判斷矩陣進行一致性檢驗，步驟如下：

計算一致性指標CI

先計算矩陣的最大特征根λmax，然后計算CI：

查找相應的平均隨機一致性指標RI。對n=1，…，9，Saaty給出了RI的標準值(見表4)。

表4 RI的標準值

計算一致性比例CR

當CR<0.10時，認為判斷矩陣的一致性是可以接受的，否則應對判斷矩陣作適當修正，然后重復進行a～c步，直至CR<0.10。

1.4 層次總排序及一致性檢驗

上面我們得到的是一組元素對其上一層中某元素的權重向量。我們最終要得到最低層中各救生策略(C1、C2、C3)元素對于目標A的排序權重，從而進行策略選擇。

總排序權重的獲得需要自上而下地將單準則下的權重進行合成。計算方法如下：

設上一層次(A層)包含A1，…，Am共m個因素，它們的層次單排序權重分別為a1，…，am。又設其后的下一層次(B層)包含n個因素B1，…，Bn，它們關于Aj的層次單排序權重分別為b1j，…，bnj(當Bi與Aj無關聯時，bij=0)。按照下式計算B層中各因素關于總目標的層次總排序權重b1，…，bn，即：

其中，i=1，…，n

對層次總排序也需要作一致性檢驗，檢驗仍象層次總排序那樣由高層到低層逐層進行。設B層中與Aj相關的因素的成對比較判斷矩陣在單排序中經一致性檢驗，求得單排序一致性指標為CI(j)，(j=1，…，m)，相應的平均隨機一致性指標為RI(j)、CI(j)、RI(j)已在層次單排序時求得)，則B層總排序隨機一致性比例為

當CR<0.10時，認為層次總排序結果具有較滿意的一致性并接受該分析結果。

2 驗算與結論

對上述決策模型，我們進行了試驗性質的計算機軟件編程和測試(見圖2)。

圖2 模型編程驗算

在調試正確的基礎上，提供給部分人員試用，通過對上述模型的編程使用與驗算，得到如下結論。

1)利用層次分析法構建棄艇脫險輔助決策模型，可以實現對問題的快速決策的功能，尤其在信息不完備條件下，為潛艇指揮員提供一個簡便、靈活而又實用的輔助決策手段和工具。

2)層次分析法受到人的主觀價值觀、主觀判斷、主觀意向等因素的影響較大，并不能夠代替人工思維，能夠去除人工思維中的不確定性和混亂性，使得結果更趨合理和可靠。

3)上述層次結構中的準則層可以進一步擴展，得到更加合理的決策結果。